Урок по математике 11 класс

Урок в 11 классе по теме «Логарифмическая функция, её свойства и график»

Учитель Курдина О.В.

Цели урока:

Образовательные:

• Систематизировать и обобщить знания и умения учащихся по ранее изученным темам.

• Создать условия для отработки обучающимися навыков, необходимых при решении заданий ЕГЭ.

Развивающие:

• Развивать творческую самостоятельность мышления обучающихся, их интеллектуальные качества: способность к «видению» проблемы.

• Развивать научную аргументированную речь, умение чётко и ясно излагать свои мысли, подходить к решению задач с исследовательской позиции.

Воспитательные:

• Воспитывать информационную культуру, самостоятельность, аккуратность и добросовестность при выполнении заданий.

• Создавать условия для становления субъектной позиции обучающихся при подготовке к итоговой аттестации, повышения их мотивации.

• Воспитание воли и настойчивости в достижения поставленной цели; упорства и интереса к решению задачи с позиции исследователя.

Ход урока.

1. Орг.момент: Приветствие. Сообщение темы урока, целей урока, создание позитивного настроя.

2. Проверка дом.задания (разбор заданий, вызвавших затруднения)

3. Задания на повторение и обобщение знаний: на доске записаны задания, взятые с сайтов для подготовки к ЕГЭ, часть из них решаем устно, но объясняем, но некоторые задания нужно записать в тетрадь

• Вычислить:

• 

• 

• !

• 

• 

• !

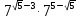
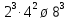
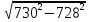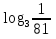
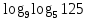
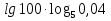• Решить уравнения:

• 

• 

• 

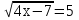
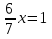
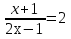
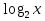• =5

• !

• !

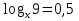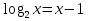Каким способом можно решить данное уравнение?

Данное уравнение можно решить методом подбора, но в этом случае есть вероятность потерять корни и можно графическим методом. Давайте рассмотрим 2 способ.

Зададим функции : у1=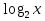 и у2=х-1, графиком первой функции будет график логарифмической функции, заданной на интервале от0 до ∞, возрастающей на всей области определения; графиком второй функции будет прямая, заданная на всей числовой прямой и также возрастающая.

Ответ: 1;2

4. Решение заданий для подготовки к ЕГЭ

В последнем задании чтобы решить уравнение мы с вами воспользовались графиком логарифмической функции. А где ещё, в каких заданиях нам могут пригодиться умение построения графика и знания свойств функций? Это задания В 14.(найти наименьшее или наибольшее значение функции на отрезке или интервале, точки максимума или минимума)

• Найти наименьшее значение функции : 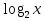на 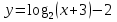Давайте вспомним свойства функции.

1.Д(у) : х+3>0; x>-3 2. т.к.основание 2>1, то на х>-3 функция возрастает 3.наименьшее значение наша функция будет принимать при х=1, у=0.

А наибольшее? (при х=5, у=1)

• Найти наибольшее значение функции : 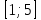на 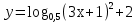сам-но

1.Д(у): х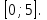

2.т.к. 0,5<1, то функция убывает на всей области определения

3. наибольшее значение функция будет принимать при х=5, у= -6.

5. Работа классу: задания из учебника №№ 42.20 (а), 42.22(а,б); 42. 23 (а,б) индивидуально у доски

6. Итог урока. Если вы на этом уроке узнали хоть немного больше того, что знали и готовы использовать эти знания в работе, значит урок прошел с пользой для всех.

7. Домашнее задание. №№ 42.20 (в), 42.22 (в), 42.23 (в)