Проект по математике 5 класс 'Удивительный мир чисел'

МБОУ Инзенская СШ №1 имени Ю.Т. Алашеева

Проект

«Удивительный мир чисел»

Работу выполнили

учащиеся 5 класса А

Руководитель проекта:

Ёлчева Н.Л.

2014 г.

Руководитель проекта

Ф.И.О.

Ёлчева Нина Леонидовна

Регион

Ульяновская область

Населённый пункт, где находится

школа

Город Инза

Название школы

МБОУ Инзенская СШ №1

Описание проекта

Тема учебного проекта

«Удивительный мир чисел»

Краткое содержание проекта

История возникновения чисел, как люди научились считать; линейные числа, фигурные числа, совершенные числа, дружественные числа.

Предмет

Математика

Класс

5 класс

Продолжительность проекта

3 недели

Основа проекта

Образовательные стандарты

Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучение смежных дисциплин.

Интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность преодолевать трудности.

Воспитание отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Дидактические цели, ожидаемый результат

В результате работы над проектом учащиеся смогут определять простые и составные числа, совершенные числа, дружественные и фигурные числа, называть удивительные свойства чисел. Будут знать имена великих математиков: Пифагор, Евклид, Эратосфен, Архимед. Научатся проводить фокусы с числами, разгадывать ребусы и головоломки, загадки с числами, строить фигурные числа.

Вопросы, направляющие проект

Основополагающий вопрос

Что есть число?

Прблемные вопрсы

1. Существует ли связь между понятием числа и геометрической фигурой?

2. Какие существуют классификации фигурных чисел?

3. Существует ли самое большое число?

Учебные вопросы

- Назвать определение фигурного числа.

- Установить виды фигурных чисел.

- Каковы закономерности процесса построения фигурных чисел?

- Какие числа называются совершенными?

- Какие числа называются дружественными?

Оценивание работы учащихся

До работы над проектом

- Формирующее оценивание стартовых знаний в форме фронтальной беседы, вводной презентации учителя.

- Список тем исследования.

- Критерии оценивания исследований учеников.

Ученики работают над проектом и выполняют задания.

- Оценивание работы учеников по предложенным дидактическим материалам.

- Обсуждение предварительных результатов в каждой группе.

- Консультация учителя.

- Работа с дидактическим материалом.

После завершения работы над проектом

- Самооценка работы группы.

- Представление результатов работы групп в виде презентации.

- Выступление на уроке-конференции.

- Рефлексия.

Описание методов оценивания

Работа над проектом начинается с того, что в ходе презентации учителя выясняются знания учащихся по данной теме, учащиеся мотивируются на проведение исследований в проекте, определяются темы исследований. Учитывая требования стандарта, составляются критерии оценивания будущих работ учащихся, по которым происходит контроль и самоконтроль в группах. Перед началом работы учащиеся знакомятся с данными критериями. В ходе работы группы заполняют таблицу продвижения по проекту, обсуждают полученные результаты, сверяют полученные результаты с критериями. Для глубокого осмысления темы для учащихся разработаны дидактические материалы. После завершения работы заполняются листы самооценки работы группы, создаётся презентация, отражающая результаты исследований и полученные выводы. Проводится урок-конференция, на котором заслушиваются выступления учащихся с итогами своей работы. Здесь оценивается глубина проведённого исследования, краткость и ёмкость формулировок, умение логично представлять ход и результаты исследования, убедительно аргументировать свою точку зрения, задавать вопросы, активность. В ходе выступления учащиеся демонстрируют результаты своей деятельности - презентации и публикации. В завершении конференции коллективно обсуждаются выводы, служащие ответом на основополагающий вопрос проекта. По итогам проекта осуществляется индивидуальная рефлексия.

Предварительные знания, умения и навыки.

Первоначальные навыки поиска информации в Интернете, исторической и учебной литературе, навыки осмысленного чтения. Первоначальные навыки работы в текстовом редакторе и Power Point.

Учебные мероприятия

1 занятие.

- Знакомство с проектом.

- Деление учащихся на группы.

- Задания по группам:

I группа - возникновение чисел, линейные числа, простые и составные числа, решето Эратосфена.

II группа - фигурные числа, их классификация; совершенные и дружественные числа.

III группа - подготовить числовые фокусы, числовые кроссворды, головоломки и ребусы с числами.

2 занятие.

Рассказ о простых и составных числах.

Рассказ о способе отыскания простых чисел - «Решето Эратосфена»

3 занятие.

Рассказ о дружественных , фигурных и совершенных числах

Практическая работа по построению фигурных чисел.

4 занятие.

Практическое занятие на логику и смекалку.

5 занятие.

Защита рефератов ( 1 группа )

Показ презентаций ( 2 группа )

Демонстрация альбома с числовыми фокусами, кроссвордами, головоломками, ребусами ( 3 группа ).

Создание комфортных условий для дифференцированного обучения

Возможности для учеников

Работа в группах позволяет ученикам выбрать для себя роль в соответствии со склонностями и интересами, чтобы быть успешным и внести свой вклад в итоговую работу:

- анализ источников;

- поиск и обработка необходимой информации по теме проекта;

- поиск и подготовка к представлению иллюстративного материала по теме проекта;

- организация и проведение совместного обсуждения результатов работы ;

- обработка результатов и представление их средствами компьютерных технологий;

- подготовка и проведение устной презентации работы группы.

Одарённые ученики

В ходе работы над проектом возможны различные пути изучения материала, которые могут выбрать сами ученики. Школьники, заинтересованные в более глубоком изучении математики, могут выйти за рамки выполняемых учебных задач, провести дополнительные исследования и расширить поле деятельности проекта.

Ученики, испытывающие трудности в обучении

В работе над проектом ученики выполняют доступные для себя, чётко определённые задачи на основе продуманного алгоритма действий. Они имеют возможность воспользоваться помощью других участников группы, проконсультироваться с учителем. Такие ученики должны почувствовать свою значимость в общем деле, почувствовать, что они могут быть успешными.

Материалы и ресурсы, необходимые для выполнения проекта

Технологии - цифровые устройства

- компьютер;

- сеть интернет;

- принтер;

- проектор.

Технологии - программное обеспечение

- электронные энциклопедии;

- мультимедийные программы;

- текстовый редактор.

Пифагор

Числа древними греками, а вместе с ними Пифагором и пифагорейцами мыслились зримо, в виде камешков, разложенных на песке или на счетной доске - абаке. По этой причине греки не знали нуля, так как его невозможно было "увидеть". Но и единица еще не была полноправным числом, а представлялась как некий "числовой атом", из которого образовывались все числа. Пифагорейцы называли единицу "границей между числом и частями", то есть между целыми числами и дробями, но в то же время видели в ней "семя и вечный корень". Число же определялось как множество, составленное из единиц. Особое положение единицы как "числового атома", роднило ее с точкой, считавшейся "геометрическим атомом". Вот почему Аристотель писал: "Точка есть единица, имеющая положение, единица есть точка без положения". Таким образом пифагорейские числа в современной терминологии - это натуральные числа. Числа-камешки раскладывались в виде правильных геометрических фигур, эти фигуры классифицировались. Так возникли числа, сегодня именуемые фигурными. Итак, фигу́рные чи́сла - общее название чисел, геометрическое представление которых связано с той или иной геометрической фигурой

1. Линейные числа

Линейные числа - самые простые числа, которые делятся только на единицу и на самих себя и вследствие этого могут быть изображены в виде линии, составленной из последовательно расположенных точек. Примером линейного числа является - число 5

( л и н е й н о е ч и с л о 5 )

Эти числа называются простыми. Более двух тысяч лет назад в Греции знаменитый математик Эратосфен придумал очень остроумный способ выискивать простые числа. Он предложил для этого применять особое решето, сквозь которое все ненужные числа будут просеиваться, а все нужные - простые - оставаться.

Чудесное решето назвали решетом Эратосфена. А действует оно следующим образом.

Запишем все числа, начиная с двойки, по порядку:

2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; . . .

Такой ряд чисел называется натуральным рядом. Выбросим из этого ряда те числа, которые, которые наверняка не являются простыми, то есть делятся не только на себя, но и на другие числа. Сначала отбросим те числа, которые делятся на два. Затем отсеем те числа, которые делятся на три. Всё меньше и меньше остаётся чисел в решете. А дальше выбросим все числа, которые делятся на 5, потом те, что делятся на 7 и так далее. Так постепенно из ряда натуральных чисел будут выбывать составные числа, а простые останутся.

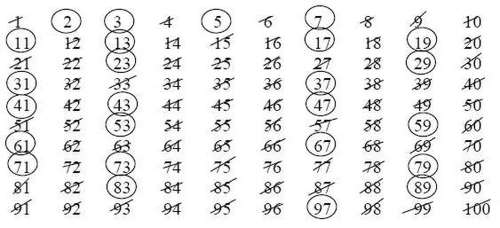
Теперь мы уже знаем очень много простых чисел. Все зачёркнутые числа, кроме 1, являются составными. Число 1 не является простым числом, но оно относится к линейным числам.

2. Плоские числа. Телесные числа.

Плоские числа - числа, представимые в виде произведения двух сомножителей, (или составные): 4; 6; 8; 10; . . .

(число 6) (число 10)

Эти числа можно расположить в две линии.

Телесные числа - числа, представимые в виде произведения трёх сомножителей: 8; 12; 16; 18; . . .

3. Многоугольные числа.

Выкладывая различные правильные многоугольники, мы получаем разные классы многоугольных чисел. Предположительно от фигурных чисел возникло выражение «Возвести число в квадрат или в куб»

Треугольные числа.

Нарисованные и попарно соединённые три точки создают правильный (равносторонний) треугольник. А если точек четыре - можно ли их расположить аналогичным способом? Оказывается, нет. Пять точек - тоже нет. А вот шесть точек расположить в требуемом порядке уже можно. При этом новый треугольник получается линейным увеличением последнего в три раза. Чтобы впечатление треугольника сохранялось нужно добавить четыре точки. Соответствующий треугольник получается линейным увеличением исходного в три раза.

Продолжая добавлять точки, будем получать всё новые и новые треугольники.

В приведённых примерах точек сначала было три, потом шесть, затем десять и так далее. Эти числа по вполне понятным причинам называются треугольными. Простейшими из этих чисел являются - !; 3; 6; 10; 15; 21; 28; 36; . . .

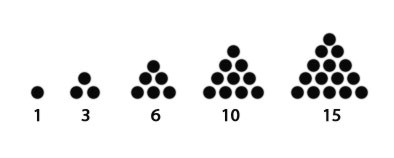
1

3=1+2

6=1+2+3

10=1+2+3+4

15=1+2+3+4+5

21=1+2+3+4+5+6 и т.д.

Любое треугольное число можно представить в виде , где n - порядковый номер числа.

Треугольные числа обладают следующими свойствами:

1. Сумма двух последовательных треугольных чисел даёт полный квадрат - квадратное число.

2. Чётность элемента последовательности меняется с периодом 4: нечётное, нечётное, чётное, чётное, . . .

Подсчитаем с помощью рисунка несколько первых треугольных чисел и составим таблицу.

№

п/п

1

2

3

4

5

6

7

Треугольное число

1

3

6

10

?

?

?

А можно ли продолжить таблицу дальше, без помощи рисунков? Сделать это совсем просто, если понять правило, по которому каждое следующее треугольное число получается из предыдущего. Посмотрите на таблицу: третье треугольное число получается, если ко второму прибавить число 3, т. е. его номер; четвертое треугольное число получается добавлением к третьему числу 4 и т. д.

А можно ли найти какое-нибудь треугольное число, не вычисляя всех предыдущих? Попробуем найти треугольное число под номером 10. Десятое треугольное число равно сумме:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +10.

Для подсчета этой суммы запишем ее слагаемые в обратном порядке и расположим суммы одна под другой:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +10.

10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 +1.

Сумма каждой пары, расположенных друг под другом, равна 11. Всего таких сумм 10. Поэтому удвоенная сумма равна 10 · 11. А само треугольное число (10 · 11) : 2 =55.

Порешаем?

1. а) Шары укладывают в равносторонние треугольники. В пятнадцатом треугольнике 120 шаров. Сколько шаров в 16 треугольнике? В четырнадцатом?

б) Заполни указанную часть таблицы

№

п/п

17

18

19

20

21

22

23

24

25

Треугольное

число

240

2.

а) Шары уложили в равносторонний треугольник, в котором 25 рядов. Сколько потребовалось шаров?

б) Чему равно треугольное число с номером 35? С номером 50? С номером 1000?

3.

а) Несколько шаров уложили на плоскости в равносторонний треугольник - остались лишними 3 шара. А когда построили треугольник, сторона которого содержит на 1 шар больше, то не хватило 4 шаров. Сколько было шаров?

б) Несколько шаров уложили на плоскости в равносторонний треугольник - остались лишними 24 шара. А когда построили треугольник, сторона которого содержит на один шар больше, то не хватило 11 шаров. Сколько было шаров?

4.

В каком порядке идут четные и нечетные числа в последовательности треугольных чисел? Четным или нечетным является число с номером 17, 18, 19, 20? Четным или нечетным является число с номером 60, 78, 35?

5.

Найдите сумму:

а) 15-го и 16-го треугольных чисел;

б) 47-го и 48-го треугольных чисел.

Желаем успеха!

Треугольные числа связаны с именем великого древнегреческого математика и философа Пифагора, который жил в VI в. До н. э. Пифагор использовал квадратные, пятиугольные числа. У него не только плоские фигуры изображали числа. Были также и пирамидальные числа, и кубические …

Квадратные числа.

Нарисованные точки образуют правильную геометрическую фигуру - квадрат. Квадратными числами называются числа ряда: 1; 4; 9; 16; 25; 36; 49; 64; 81; 100; . . .

1 4 9 16 25

1=1х1

4=2х2

9=3х3

16=4х4

25=5х5 и т.д.

Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами.

Любое квадратное число можно представить в виде , где n - порядковый номер числа.

Пятиугольные числа.

Пятиугольные числа - это числа, которые образуют правильный пятиугольник.

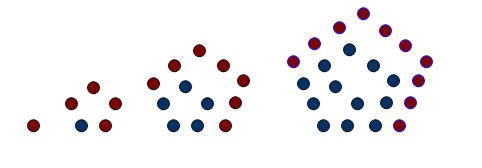
1 5 12 22

Любое пятиугольное число можно записать в виде , где n- порядковый номер числа.

Совершенные числа

Совершенное число (др.-греч. ἀριθμὸς τέλειος) - натуральное число, равное сумме всех своих собственных делителей (т. е. всех положительных делителей, отличных от самого числа). По мере того как натуральные числа возрастают, совершенные числа встречаются всё реже.

• - шесть. Натуральное четное число. Факториал 3!, Регулярное число (Число Хемминга), Совершенное число. В ряду натуральных чисел находится между числами и .

Делители числа 6 - 1; 2; 3 - собственные делители.

6=1+2+3

• - двадцать восемь. Натуральное четное число. Совершенное число. В ряду натуральных чисел находится между числами и .

Делители числа 28 - 1; 2; 4; 7; 14 - собственные делители.

28=1+2+4+7+14

• - четыреста девяносто шесть. Натуральное четное число. Совершенное число. В ряду натуральных чисел находится между числами и .

Четвёртое совершенное число - 8128,

пятое - 33 550 336,

шестое - 8 589 869 056,

седьмое - 137 438 691 328 . . .
В диапазоне от 1 до 100 всего 2 числа- 6 и 28

Сказка о совершенных числах

28 сентября число 28 решило пригласить в гости всех своих делителей, меньших, чем оно само. Первой прибежала единица, за ней двойка, за ней 4; 7; 14. Когда все гости собрались, число 28 увидело, что их немного. Оно огорчилось и предложило, чтобы каждый из гостей привел ещё и своих делителей. (Сколько придет новых гостей?). Единица объяснила числу 28, что новые гости не придут.

Чтобы утешить число 28 , его гости соединились знаком "+". И, о чудо, сумма оказалась равной самому числу 28! Единица сказала, что всякое число, которое равно сумме своих меньших делителей, называется совершенным. Число обрадовалось и спросило, какие числа есть ещё совершенные. Всезнающая единица ответила, что совершенных чисел очень мало: среди чисел до миллиона их всего четыре: 6, 28, 496 и число 8128. Известно довольно много четных совершенных чисел, но не известно ни одного нечетного совершенного числа. Также неизвестно, конечно ли количество совершенных чисел. Возьмём совершенное число - 6. На какие числа делится это число? На 1, на 2 и на 3. Теперь сложим эти три числа: 1 + 2 + 3 = 6 Или вот другое совершенное число - 28, - Помните, какие у него младшие делители - 1, 2, 4, 7 и 14. Сложим их: 1 + 2 + 4 + 7 + 14 = 28. Значит, совершенные числа равны сумме всех своих младших делителей. К сожалению, совершенных чисел всего двадцать четыре: 6, 28, 496,8128, 130 816… Дальше они растут всё быстрее и быстрее, а вычислять их всё сложнее и сложнее. Может быть вам доведётся найти новое совершенное число.

Дружественные числа

Дружественные числа - это пара чисел, обладающих таким свойством: сумма собственных делителей (не считая самого числа) первого из них равна второму числу, а сумма собственных делителей второго числа равна первому числу.

Они открыты древнегреческими учеными - последователями Пифагора. Недаром знаменитый греческий математик Пифагор сказал: «Друг - это второе я!» - и при этом сослался на числа 220 и 284. Они замечательны тем, что каждое из них равно сумме младших делителей другого числа. Какие делители у числа 284?

1, 2, 4, 71, 142.

А у числа 220 делители:

1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110.

Попробуем сложить делители каждого числа:

1 + 2 + 4 + 71 + 142 = 220,

1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284.

Вот почему эти числа называются дружественными. Пифагорейцы знали только одну пару дружественных чисел: 220 и 284. Вторая дружественная пара (1184 и 1210) была найдена в 1867 году шестнадцатилетним итальянцем Б. Паганини. Пары дружественных чисел образуют последовательность: 220, 284, 1184, 1210, 2620, 2924, 5020, 5564, 6232, 6368, …

Две стихии господствуют в математике - числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. Само возникновение понятия числа - одно из гениальнейших проявлений человеческого разума. Действительно, числа не только что-то измеряют. Числа сравнивают и вычисляют, рисуют и проектируют, сочиняют и играют, делают умозаключения и выводы