Урок разноуровневого повторения на тему 'Производная' (11 класс)

Урок разноуровневого обобщающего повторения по теме :

Зайцева Нина Михайловна, учитель математики МБОУСОШ №31

с. Шаумян Туапсинского района Краснодарского края.

Цель урока:

1. Обобщить теоретические знания по теме «Производная».

2. Рассмотреть решение задач, связанных с этой темой, базового и повышенного уровня сложности.

3. Организовать работу учащихся на уровне, соответствующем уровню уже сформированных у них знаний.

Оборудование:

1. Графики функций и их производные.

2. Тесты.

Группа 1- не справляются с заданиями базового уровня.

Группа 2 - справляются с заданиями базового уровня и не справляются с повышенным уровнем.

Группа 3 - успешно решают задания повышенного уровня.

Ход урока.

1. Организационный момент.

   • Приветствие.

   • Сообщение цели урока.

   • Объявление плана урока.

2. Основная часть.

1. Историческая справка о происхождении терминов и обозначений по теме. (сообщение ученика)

Производная - одно из фундаментальных понятий математики. Оно возникло в XXVII веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: определение скорости прямолинейного движения и построения касательной к прямой. Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время. И. Ньютон в основном опирался на физическое представление о мгновенной скорости движения, считая его очевидным и сводя

к нему другие случаи производной, а Г. Лейбниц использовал понятие бесконечно малой. Исчисление созданное Ньютоном и Лейбницем, получило название дифференциального исчисления. С его помощью был решен целый ряд задач теоретической механики, физики и астрономии. В частности, используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XXVII века. С помощью тех же методов математики изучали в XXVII и XXVIII веках различные кривые, нашли кривую, по которой быстрее всего падает материальная точка, научились находить кривизну линий. Большую роль в развитии дифференциального исчисления сыграл Л. Эйлер, написавший учебник "Дифференциальное исчисление".

Основные понятия дифференциального исчисления долгое время не были должным образом обоснованы. Однако в начале XIX века французский математик О. Коши дал строгое построение дифференциального исчисления на основе понятия предела. Применяемая сейчас система обозначений для производной восходит к Лейбницу и Лагранжу. В настоящее время понятие производной находит большое применение в различных областях науки и техники.

2. Блиц опрос.

1. Дать определение производной?

2. Чему равна производная постоянной величины? Назвать формулу.

3. Чему равна производная 5, 10, 15 и т.д.?

4. Чему равна производная от x?

5. Чему равна производная степенной функции? Формула. Правило.

6. Чему равна производная x², x⁵, x¹⁰ и т.д.?

7. Чему равна производная ?

8. Чему равна производная ?

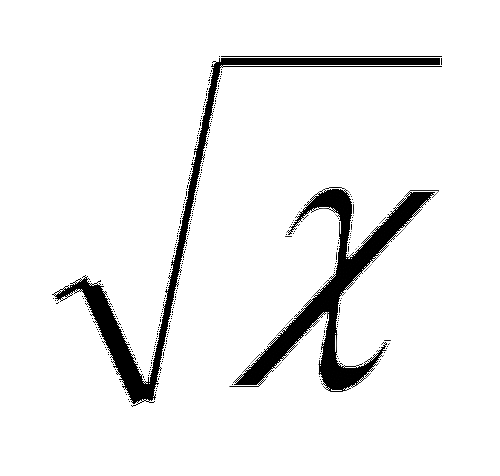9. Назовите производные тригонометрических функций?

10. Чему равна производная суммы (разности) двух функций?

11. Чему равна производная произведения двух функций?

12. Чему равна производная произведения двух функций, в котором один из сомножителей постоянный?

13. Чему равна производная дроби?

14. Чему равна производная сложной функции?

15. Достаточный признак возрастания (убывания) функции.

16. Алгоритм нахождения промежутков возрастания и убывания функции.

17. Необходимое условие экстремума.

18. Алгоритм отыскания экстремумов.

3. Работа по рисункам на доске.

а) По характеру изменения графика функции указать на каких промежутках производная положительна, на каких - отрицательна (каждая функция определена на R).

y

y

y

1

1

x

x

0

1

0

1

1

x

0

1

Рис.1 рис. 2 рис. 3

б

y) Дан график производной функции. Найдите промежутки возрастания и убывания функции.

1

x

0

в

y

y) Даны графики производных функций. При каких значениях переменной х функции имеют точки максимума и минимума? Назовите эти точки.

y

3

1

2

1

x

x

1

x

0

1

-

0

1

0

-4

-3

-2

-1

1

2

3

4

-1

-2

-3

Рис. 4 рис. 5 рис. 6

г

y

y

y

y

y) Для каждой из функций, графики которых изображены в верхнем ряду, найдите график производной в нижнем ряду.

1

1

1

1

1

x

0

1

x

0

1

x

0

1

x

1

0

x

1

-

Р

y

y

y

y

yис. 7 рис. 8 рис. 9 рис. 10 рис. 11

1

1

1

1

1

x

1

x

x

x

x

0

1

1

0

1

0

1

0

1

a) б) в) г) д)

3. Разноуровневая самостоятельная работа.

Группа 1 - зеленая карточка, группа 2 - голубая карточка, группа 3 - розовая карточка.

IV. Задание на дом. № 219, 230 стр.293.

Зеленая карточка

Вариант 1.

1. Найдите значение производной функции y(x) = 3x³ +2x² +x + 1 в точке c абсциссой x₀ = - 1. 1) 6 2) 5 3) 4 4) 3

2. Найдите производную функции y = 2^x + cosx. 1) y′ = 2^x - sinx 2) y′ = 2^xln2 - sinx 3) y′ = x4^x-1 - 2sinx 4) y′ = 2^xln2 - cosx

3. Найдите тангенс угла наклона касательной, проведенной к графику функции у = 4х - х² в точке с абсциссой х₀ = - 3. 1) - 8 2) 10 3) - 4 4) 3

4. Для каждой функции укажите график её производной.

y

y

y

y

y 1) у = 2х - 7 2) у = 7 3) у = 7 - 4) у = х² - 7 5) у = - х² + х

1

1

1

1

1

x

0

1

x

0

1

x

0

1

x

0

1

0

x

1

а) б) в) г) д)

5. Найдите минимум функции у = х³ - 27х + 26.

Зеленая карточка

Вариант 2.

1. Найдите значение производной функции y(x) = 3x⁴ - 2x² + x - 1 в точке c абсциссой x₀ = 1.

1) 9 2) 5 3) 4 4) 6

2. Найдите производную функции y = tgx + x² 1) 2) 3) 4) y′ = ctgx + 2x

3. Найдите угловой коэффициент касательной к кривой в точке М(4;5) 1) 1 2) 4 3) - 5 4) 8

4. Для каждой функции укажите график её производной.

y

y

y

y

y1) 2) 3) у = 3 + х³ 4) у = 2 - 2х 5) у = - 2

1

x

1

x

1

x

0

1

1

1

1

0

1

0

1

x

0

1

x

0

1

a) б) в) г) д)

5. Найдите максимум функции у = х³ - 27х = 26.

Голубая карточка.

Вариант 1.

1. Найдите значение производной функции y = ln(х - 3) в точке х₀ = 2 1) 1 2) - 1 3) 0 4) 3

2. Найдите производную функции y = sin4x - x⁴. 1) y′ = 4 cos3x - 4x³ 2) y′ = 4sin4x - 3x³ 3) y′ = - 4sin4x - 3x³ 4) y′ = 4 cos4x - 4x³

3. Найдите абсциссу точки графика функции ƒ(х) = 14х² - 27х + 15, в которой касательная наклонена под углом 45⁰ к оси абсцисс.

1) 2) 3) 2 4) 1

4. Для каждой функции укажите график её производной.

y

y

y

y

y1) у = 2х - х³ 2) 3) 4) 5) у = 3х

1

1

1

x

0

1

0

x

1

1

1

1

x

0

1

x

0

1

x

0

1

a) б) в) г) д)

y

5

1

x

0

1

. На рисунке изображен график производной функции у = ƒ(х), определённой на отрезке [-4; 5]. Найдите сумму точек экстремума функции у = ƒ(х).

Голубая карточка.

Вариант 2.

1. Найдите значение производной функции y = ln(5 - 2х) в точке х₀ = 2 1) 0 2) 1 3) -1 4) -2

2. Найдите производную функции y = sin(4x - 5) - x⁴.

1) y′ = 4cos4x - 4x³ 2) y′ = 4sin(4x - 5) - 4x³ 3) y′ = 4sin4x - 4x³ 4) y′ = 4cos(4x - 5) - 4x³

3. Материальная точка движется по закону x(t) = t³ - 5t² + 6t + 7 ( x- перемещение в м, t - время в с). Через сколько секунд после начала движения ускорение точки будет равно 8 м/с² ?

1) 1 2) 2 3) 3 4) 4

4. Для каждой функции укажите график её производной.

y

y

y

y

y1) у = - 2х 2) у = х³ - 3х 3) 4) у = х² - 2х 5)

1

1

1

1

1

1

x

0

1

x

0

1

x

0

1

x

0

1

x

0

a

y) б) в) г) д)

5

3

2

1

0

x

-1

-2

-3

1

2

3

4

5

6

7

8

9

10. На рисунке изображен график производной функции у = ƒ(х), определённой на отрезке [0; 10]. Укажите точку, в которой функция у = ƒ(х) достигает своего наибольшего значения.

Розовая карточка.

Вариант 1.

1. Найдите значение функции ƒ(х) = 2х³ -0,5х²- х в точке максимума. 1) 2) 3) 4)

2. Найдите производную функции y = (3x + 2) ctgx.

1) 2) y′ = 3ctgx - (3x + 2)sinx 3)

4) y′ = 3ctgx + (3x + 2)sinx

3. Найдите наибольшее значение функции ƒ(х) =х⁴ - 2х² + 4 на отрезке [-2;2]

4) Для каждой функции укажите график её производной.

y

y

y

y

y1) 2) 3) 4) 5) y = (x - 2)³

x

0

1

1

1

x

0

1

x

1

x

1

x

0

1

0

1

0

1

а) б) в) г) д)

5. Прямая, проходящая через начало координат, касается графика функции y = g(x) в точке F(2;3). Найдите g′ (2).