- Учителю
- Урок-презентация 'Функция y=kx^2, её свойства и график' (8 класс)
Урок-презентация 'Функция y=kx^2, её свойства и график' (8 класс)
Государственное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа с. Исаклы
муниципального района Исаклинский Самарской области
Конспект урока
по теме:
«Функция 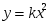 , её свойства и график»
, её свойства и график»
8 класс
Выполнила: учитель математики
Валиева Фанузя Галимзяновна
Исаклы 2015
Конспект урока
Тема урока: Функция  , её свойства и график.
, её свойства и график.
Тип урока:
-
по основной дидактической цели: урок изучения нового материала;
-
по основному способу проведения: сочетание различных форм занятий;
-
по основным этапам учебного процесса: урок образования понятий, установления законов и правил;
-
по форме проведения: комбинированный урок;
-
по целевой установке: урок-исследование.
Цели урока:
-
образовательные - сформировать понятие функции
 , сформировать умение строить график функции
, сформировать умение строить график функции  ;
; -
развивающие - развитие мышления ( учитель ставит ученикам задачу, для решения которой у учеников еще нет необходимых знаний), развитие творческого мышления (через использование творческих задач), развитие памяти (на этапе актуализации опорных знаний и способов действий);
-
воспитательные - формирование учебно-коммуникативных, учебно-интеллектуальных умений, воспитание интереса к изучению математики.
Задачи урока:
Формировать:
-
умение отличать квадратичную функцию
 от функций других видов (прежде всего линейных);
от функций других видов (прежде всего линейных); -
умение определять свойства функции
 по ее графику;
по ее графику; -
умение строить график функции
 , опираясь на ее свойства;
, опираясь на ее свойства; -
способность работать в группе, строить продуктивное взаимодействие при выполнении познавательных задач;
-
умение осуществлять расширенный поиск дополнительной информации о функции
 с использованием ресурсов Интернета;
с использованием ресурсов Интернета; -
умения высказывать свое мнение, делать выводы;
Развивать: мышление, творческое мышление, память, математический язык, умение осуществлять самостоятельную деятельность на уроке.
Общие методы обучения:
-
по источнику знаний: беседа (ученики беседовали с учителем на разных этапах урока), метод демонстрации (показ презентации), упражнения;
-
по характеру познавательной деятельности: объяснительно-иллюстративный (учитель объяснял новый материал, подкрепляя новые данные примерами на доске и демонстрацией презентации с наглядными примерами), репродуктивный (ученики выполняли действия по образцу), проблемный (на этапе решения творческих задач), исследовательский (на этапе изучения нового материала учащиеся исследовали свойства функции
 ).
).
Специальные методы обучения: анализ, синтез (при решении учениками новых заданий).
Формы обучения: фронтальная, групповая.
Оборудование: меловая доска, интерактивная доска, компьютер, проектор, презентация, подключение к сети Интернет, карточки с заданиями.
Этапы урока:
-
Организационный момент (1 мин).
-
Актуализация опорных знаний и способов действий (5 мин).
-
Ознакомление с новым материалом (15 мин).
-
Закрепление нового материала (20 мин).
-
Постановка домашнего задания (1 мин).
-
Подведение итогов урока (3 мин).
Выделение полного квадрата
Формулы координат вершины
Способы построения
По направлению ветвей и характерным точкам
С помощью преобразований графика y=x2
Интервалы
знакопостоянства
Четность.
Симметричность графика
Монотонность
Точки экстремума
Свойства
Вид и расположение графика в зависимости от коэффициентов
Функция
y = ax2 + bx + c
Функция
y = x2
График функции
Свойства
Функция
y = ax2
График функции
Свойства
График функции
Логико-структурная схема
Ход урока
Этап урока
Задачи урока
Содержание урока
Формы работы
Методы
УУД
Контроль
Время
Деятельность учителя
Деятельность учащихся
Организационный момент
Подготовка учащихся к работе
- Здравствуйте ребята, присаживайтесь.
- На сегодняшнем уроке вы будете работать в группах. Результат работы группы будет зависеть от каждого из вас.
Учащиеся рассаживаются, слушают учителя.
1 мин
Актуализация опорных знаний и способов действий
Обеспечение мотивации и принятия учащимися цели учебной деятельности, актуализация опорных знаний и умений
Постановка целей урока
Формировать умения высказывать свое мнение, делать выводы
- Итак, начнем. Откройте тетради, запишите число, классная работа.
- Первое задание.
Задание 1. Распределите данные функции на две группы: 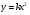 ,
, 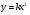 ,
, 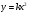 ,
, 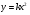 ,
, 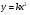 ,
, 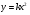 ,
, 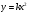 (задание записано на слайде 2).
(задание записано на слайде 2).
Проверка задания осуществляется фронтально с помощью интерактивной доски (на слайде 3появляется верное решение).
- По какому признаку вы разделили функции на две группы?
- Верно. А теперь обратите внимание на слайд 4. Здесь изображены два рисунка. С помощью функций какой группы можно получить данные рисунки?
- Правильно. А как называются функции, которые вы объединили во второй группе?
- Верно. С линейной функцией и функцией 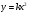 вы уже знакомы. Сегодня на уроке мы познакомимся с функцией
вы уже знакомы. Сегодня на уроке мы познакомимся с функцией  , где
, где 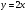 - некоторое число, в начале урока вы такие функции отобрали в отдельную группу. Запишем тему нашего урока «Функция
- некоторое число, в начале урока вы такие функции отобрали в отдельную группу. Запишем тему нашего урока «Функция  , её свойства и график».
, её свойства и график».
- Давайте подумаем, какие цели мы ставим перед собой на сегодняшний урок.
Учитель обобщает и корректирует сформулированные учениками цели, после чего они появляются на слайде (Слайд 5).
Записывают в тетради число, классная работа.
Самостоятельно выполняют первое задание в тетрадях.
Один из учеников по просьбе учителя рассказывает, как распределил функции на две группы.
- В первой группе функции в которых содержится 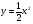 , а во второй -
, а во второй - 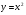 .
.
Учащиеся рассматривают рисунки. Один из учеников отвечает на вопрос:
- Первый рисунок может быть получен с помощью функций первой группы, а второй - функций второй группы.
- Линейные.
Слушают учителя. Записывают в тетради тему урока.
Учащиеся предлагают варианты целей урока.
Фронтальная
Наглядно-практические
Беседа
Анализ Синтез
Познавательные: анализ объектов с целью выделения признаков; синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты;выбор оснований и критериев для сравнения, классификации объектов.
Коммуникативные: самостоятельное выделение и формулирование познавательной цели.
Регулятивные: осуществлять целеполагание.
Устный
5 мин
Изучение нового материала
Исследовать свойства функции 
Развивать творческое мышление учащихся
Формировать умения высказывать свое мнение, делать выводы
Для исследования свойств функции учащимся в группах предлагается выполнить задание на карточках (Приложение 1). Учащимся необходимо построить график предложенной функции.
Результат работы каждой группы размещается на доске.
- Посмотрите на графики этих функций. Они отличаются от графика известной вам функции 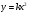 (график на слайде 6) и между собой. Ваша задача определить, от чего зависит вид параболы?
(график на слайде 6) и между собой. Ваша задача определить, от чего зависит вид параболы?
- Какими свойствами обладают функции вида  и от чего они зависят?
и от чего они зависят?
Учитель уточняет и обобщает ответы учеников, демонстрируются свойства функции с помощью ролика (слайд 7).
На слайде появляются свойства функции  при k положительном и отрицательном.
при k положительном и отрицательном.
Учащиеся были разделены на группы до начала урока. Каждая группа работает со своим заданием. График функции строится на клетчатой бумаге формата А4, с изображенной системой координат.
Каждая группа получает инструктивную карту (Приложение 2). Учащиеся выполняют предложенные задания и делают вывод о свойствах функции  .
.
Представитель каждой группы перечисляет сделанные выводы.
Свойства записываются в тетрадь.
Групповая
Анализ Синтез
Исследовательский
Беседа
Объяснительно-иилюстративный
Познавательные: анализ объектов с целью выделения признаков; синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты.
Личностные: умение вести диалог на основе равноправных отношений и взаимного уважения.
Устный
15 мин
Свойства функции  при
при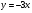 :
:
-
Область определения функции вся числовая прямая.
-
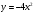 при
при 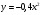 ;
; 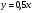 при
при 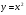 .
. -
 - непрерывная функция.
- непрерывная функция. -
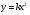 наим= 0 (достигается при
наим= 0 (достигается при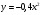 ),
), 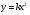 наиб - не существует.
наиб - не существует. -
Функция
 возрастает при
возрастает при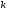 и убывает при
и убывает при 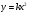 .
. -
Область значений функции
 - луч
- луч 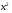 .
.
Свойства функции  при
при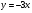 :
:
-
Область определения функции вся числовая прямая.
-
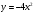 при
при 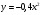 ;
; 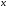 при
при 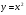 .
. -
 - непрерывная функция.
- непрерывная функция. -
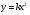 наиб = 0 (достигается при
наиб = 0 (достигается при 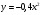 ),
), 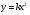 наим- не существует.
наим- не существует. -
Функция
 возрастает при
возрастает при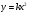 и убывает при
и убывает при 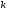 .
. -
Область значений функции
 - луч
- луч 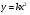 .
.
Закрепление изученного материала
Закрепить полученные знания
Развивать творческое мышление учащихся
- А теперь попробуем на практике применить полученные знания.
Задание. Подберите математическую запись функции для каждого графика.
Проверка осуществляется с помощью интерактивной доски (слайд 8).
Демонстрация оптического свойства параболы с помощью интерактивной доски (слайд 9).
Задание. Выполните указания инструктивной карточки. Озаглавьте полученный рисунок. Если необходимо, дорисуйте необходимые элементы. (Приложение 5)
Задание предлагается на карточках (Приложение 3). Каждый ученик выполняет задание самостоятельно.
Один из учеников у доски выполняет задание, которое автоматически проверяется. В случае ошибки ученик может выполнить задание повторно.
Один из учеников рассказывает об оптическом свойстве параболы (сообщение приготовлено к уроку заранее (Приложение 4)).
Учащиеся выполняют задания в группах. После полученные рисунки вывешиваются на доске.
Фронтальная
Групповая
Упражнения
Метод демонстраций
Упражнения
Проблемный
Познавательные: осуществлять расширенный поиск информации с использованием ресурсов Интернета
Устный
5 мин
5 мин
10 мин
Постановка домашнего задания
Учитель сообщает домашнее задание § 17, № 17.4, 17.6, 17.18. Комментирует задания.
Записывают домашнее задание.
Фронтальная
Объяснение
1 мин
Подведение итогов урока
Сделать выводы по уроку
- Подводя итоги урока, оцените себя, ответив на следующие вопросы (слайд 10).
Учащиеся отвечают на вопросы или заканчивают фразу.
Фронтальная
Личностные, регулятивные: способность рефлексировать.
Коммуникативные: выстраивание логической речи.
3 мин
Приложение 1
1 группа: Построить по точкам график функции 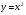 .
.
2 группа: Построить по точкам график функции 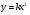 .
.
3 группа: Построить по точкам график функции 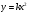 .
.
4 группа: Построить по точкам график функции 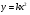 .
.
5 группа: Построить по точкам график функции 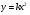 .
.
6 группа: Построить по точкам график функции 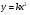 .
.
Приложение 2
Инструктивная карта № 1
-
Сравните графики функций
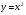 и
и 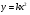 ,
, 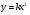 и
и 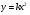 ,
, 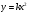 и
и 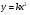 . Сделайте вывод.
. Сделайте вывод. -
Сравните графики функций
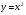 ,
, 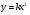 и
и 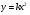 и
и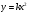 . Сделайте вывод.
. Сделайте вывод. -
Опишите свойства функции
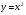 .
.
Инструктивная карта № 2
-
Сравните графики функций
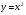 и
и 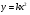 ,
, 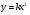 и
и 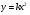 ,
, 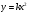 и
и 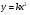 . Сделайте вывод.
. Сделайте вывод. -
Сравните графики функций
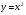 ,
, 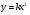 и
и 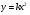 и
и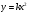 . Сделайте вывод.
. Сделайте вывод. -
Опишите свойства функции
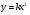 .
.
Инструктивная карта № 3
-
Сравните графики функций
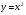 и
и 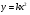 ,
, 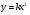 и
и 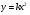 ,
, 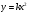 и
и 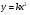 . Сделайте вывод.
. Сделайте вывод. -
Сравните графики функций
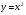 ,
, 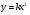 и
и 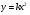 и
и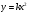 . Сделайте вывод.
. Сделайте вывод. -
Опишите свойства функции
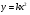 .
.
Инструктивная карта № 4
-
Сравните графики функций
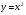 и
и 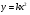 ,
, 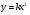 и
и 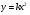 ,
, 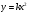 и
и 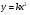 . Сделайте вывод.
. Сделайте вывод. -
Сравните графики функций
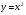 ,
, 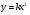 и
и 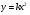 и
и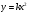 . Сделайте вывод.
. Сделайте вывод. -
Опишите свойства функции
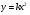 .
.
Инструктивная карта № 5
-
Сравните графики функций
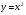 и
и 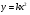 ,
, 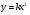 и
и 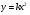 ,
, 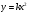 и
и 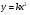 . Сделайте вывод.
. Сделайте вывод. -
Сравните графики функций
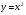 ,
, 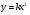 и
и 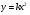 и
и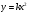 . Сделайте вывод.
. Сделайте вывод. -
Опишите свойства функции
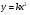 .
.
Инструктивная карта № 6
-
Сравните графики функций
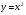 и
и 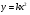 ,
, 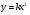 и
и 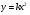 ,
, 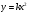 и
и 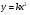 . Сделайте вывод.
. Сделайте вывод. -
Сравните графики функций
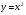 ,
, 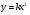 и
и 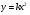 и
и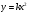 . Сделайте вывод.
. Сделайте вывод. -
Опишите свойства функции
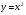 .
.
Приложение 3
Подберите математическую запись для каждого графика функции
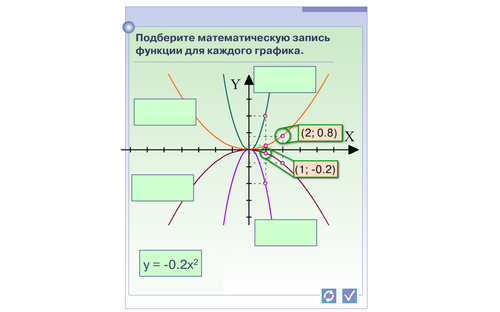
![]()
![]()
![]()
![]()
Приложение 4
Сообщение: если рассматривать параболу 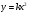 как экран, как отражающую поверхность, а в точке (0; 1/4) поместить источник света, то лучи, отражаясь от параболы-экрана, образует параллельный пучок света. Точку (0; 1/4) называют фокусом параболы. Эта идея используется в автомобилях: отражающая поверхность фары имеет параболическую форму, а лампочку помещают в фокус, тогда свет распространяется очень далеко.
как экран, как отражающую поверхность, а в точке (0; 1/4) поместить источник света, то лучи, отражаясь от параболы-экрана, образует параллельный пучок света. Точку (0; 1/4) называют фокусом параболы. Эта идея используется в автомобилях: отражающая поверхность фары имеет параболическую форму, а лампочку помещают в фокус, тогда свет распространяется очень далеко.
Приложение 5
Инструктивная карта № 1
-
Построить по точкам график функции
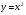 .
. -
Построить по точкам график функции
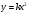 .
. -
Построить по точкам график функции
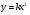 .
. -
Отметьте точки (-4; 8), (-3; 9), (-2; 8), (0; 10), (2; 8), (3; 9), (4; 8).
-
Соедините отмеченные точки.
Инструктивная карта № 2
-
Построить по точкам график функции
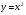 .
. -
Построить по точкам график функции
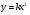 .
. -
Построить по точкам график функции
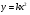 .
. -
Построить по точкам график функции
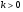 .
. -
Отметьте точки (-4; 8), (-3; 8,5), (-2; 8), (0; 9), (2; 8), (3; 8,5), (4; 8).
-
Соедините отмеченные точки.
-
Отметьте точки (-4; -8), (-3; -8,5), (-2; -8), (0; -9), (2; -8), (3; -8,5), (4; -8).
-
Соедините отмеченные точки.
Инструктивная карта № 3
-
Построить по точкам график функции
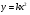 .
. -
Построить по точкам график функции
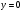 .
. -
Построить по точкам график функции
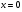 .
. -
Отметьте точки (-4; -4), (4; -4).
-
Соедините отмеченные точки.
-
Отметьте точки (-2; -8), (2; -8).
-
Соедините отмеченные точки.
Инструктивная карта № 4
-
Построить по точкам график функции
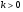 .
. -
Построить по точкам график функции
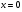 .
. -
Построить по точкам график функции
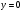 .
. -
Отметьте точки (-4; 8), (-1; -8), (-1; -5), (1; -5), (1; -8), (4; -8).
-
Соедините отмеченные точки.
Инструктивная карта № 5
-
Построить по точкам график функции
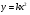 .
. -
Построить по точкам график функции
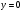 .
. -
Построить по точкам график функции
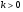 .
. -
Отметьте точки (-4; -8), (-3; -9), (-2; -8), (-1; -9), (0; -8), (1; -9), (2; -8), (3; -9), (4; -8).
-
Соедините отмеченные точки.
Инструктивная карта № 6
-
Построить по точкам график функции
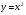 .
. -
Построить по точкам график функции
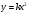 .
. -
Построить по точкам график функции
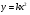 .
. -
Построить по точкам график функции
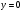 .
. -
Отметьте точки (-3; -9), (-3; 9), (3; 9), (3; -9), (-3; -9).
-
Соедините отмеченные точки.
Список литературы
1. Диктанты по алгебре. 7-11 классы. Дидактические материалы. /Г.Г. Левитас - М.: Издательство «Илекса»,2009.
2.Нестандартные уроки алгебры.8 класс./Сост. Н.А. Ким.- Волгоград, ИТД «Корифей»,2006.
3.Открытые уроки алгебры: 7-8 классы. / Н.Л. Барсукова. - М.: ВАКО,2010.