Урок - повторение по геометрии в 9 классе потеме ' треугольники '.

Урок - повторение по геометрии в 9 классе.

Тема: "Треугольники".

Цель :обобщить и систематизировать знания учащихся по теме "треугольники", повышение познавательного интереса к предмету, воспитание умения работать в коллективе, слушать своих товарищей.

Ход урока.

1. Организационный момент .В классе 20 человек .Разбиваем класс на две команды по 5 человек, остальные болельщики.

2.Разминка.Каждой команде задаются по 5 вопросов , за правильный ответ 1балл.

1 команда.

1)Какая фигура называется треугольником ?(фигура , которая состоит из трех точек , не лежащих на одной прямой и трех отрезков попарно , соединяющих эти точки.)

2)Сумма двух углов этого треугольника всегда равна 90° (прямоугольный )

3)Что общего у равнобедренного треугольника и степени?(основание)

4)Сколько различных биссектрис можно провести в треугольнике ? (три)

5)Его стороны являются касательными (треугольник, описанный около окружности )

2 команда.

1)Какие бывают треугольники ?(остроугольные, прямоугольные, тупоугольные, равнобедренные, равносторонние)

2)В каком треугольнике все высоты пересекаются в одной вершине ?

( в прямоугольном )

3)В этом треугольнике ученики всегда с трудом строят высоту ( в тупоугольном )

4) Его площадь можно найти по формуле S= (треугольник, вписанный в окружность )

5)Два угла треугольника равны 20° и 60° .Чему равен третий угол? ( 100° )

3. Решение "одной " задачи.

1команда.

B Дано:Δ ABC, АВ=7см, ВС=8см, АС=3см,АД-высота, ВЕ-

биссектриса.

ВЕ Найти: РΔ ,SΔ, АД, Sin C ,R ,r, (отрезки, на которые

А С биссектриса ВЕ делит сторону АС) АЕ,СЕ.

Решение:

а)РΔ=7+8+3=18см, р==9см

б) SΔ=√9(9-7)(9-8)(9-3)=6√3 см²

в)SΔ=ВСхАД, 6√3=х8хАД, АД=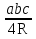см

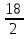г)SΔ=BCхАСхSinC. 6√3=х8х3хSinC , SinC=, угол С=60°

д)R= ==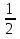= 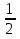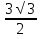cм

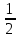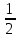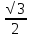е) r== =см

ж) вспомним свойство биссектрисы угла треугольника (биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам)

пусть АЕ=Хсм, тогда СЕ= 3- Х см

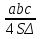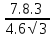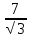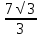= , =, Х=1,4 , АЕ=1,4см , СЕ= 1,6см.

2 команда.

B Дано:Δ ABC, АВ=5см, ВС=6см, АС=9см,СД-высота, АЕ-

биссектриса.

ВЕ Найти: РΔ ,SΔ, СД, Sin А ,R ,r, (отрезки, на которые

А С биссектриса АЕ делит сторону ВС) ВЕ,СЕ.

Решение:

а)РΔ=5+6+9=20см, р=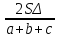=10см

б) SΔ=√10(10-5)(10-6)(10-9)=10√2 см²

в)SΔ=АВхСД, 10√2=х5хСД, СД=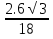см

г)SΔ=АВхАСхSinА. 10√2=х5х9хSinА , SinА=

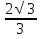
д)R= ==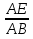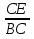см

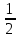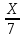е) r== см

ж) вспомним свойство биссектрисы угла треугольника (биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам)

пусть ВЕ=Хсм, тогда СЕ= 6- Х см

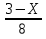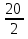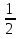= , =, Х=2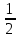 , ВЕ= 2 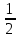см , СЕ= 3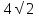см.

4.Работа с болельщиками.

Учитель называет номер решения , ученики называют номер чертежа.

а)SΔ=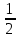

б)SΔ=х4х3=6

в)SΔ=х9х=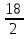

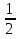
г)SΔ=√20х(20-17)х(20-15)х(20-8)=60

№1 №2 №3

В С В

3 3 4 5 8

уголА=30°

А 3 С В 3 А А 15

В

17 8

№4 В

А 15 С

5.Гонка за лидером.

Продолжите теорему.

1 команда

1)Сумма углов треугольника (равна 180 °)

2)Средняя линия треугольника (соединяющая середины двух сторон , параллельна третьей стороне и равна ее половине )

3)Если в треугольнике квадрат стороны равен сумме квадратов двух других сторон, то (этот треугольник - прямоугольный )

4)Если два угла одного треугольника равны двум углам другого треугольника ,то такие треугольники ( подобны).

5)Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без (удвоенного произведения этих сторон на косинус угла между ними, теорема косинусов )

2 команда

1)В равнобедренном треугольнике медиана , проведенная ( к основанию является биссектрисой и высотой )

2)Отношение площадей двух подобных треугольников равно ( отношению квадратов их соответствующих линейных размеров)

3)В равнобедренном треугольнике углы (при основании равны )

4)Если три стороны одного треугольника равны соответственно (трем сторонам другого треугольника, то такие треугольники равны )

5)Стороны треугольника пропорциональны ( синусам противолежащих углов, теорема синусов ).

Дополнительные вопросы:

1)Существует ли треугольник со сторонами 1см,2см,3см ? 2cм,3см,4см ?

3см,7см,11см? (нет, да, нет)

2)Подобны ли два прямоугольных треугольника, если один из углов первого равен 50°, а один из углов второго треугольника 40°? (да)

3)Угол при вершине одного равнобедренного равен 64°, а угол при основании другого равнобедренного треугольника равен 58°. Подобны лиэти треугольники ?(да )

4) В прямоугольном треугольнике АВС , угол С=90°,CosА= , катет АС=8см,

найти гипотенузу. (16см )

Болельщики решают задачи и сдают на проверку.

6.Подведение итогов.