- Учителю
- Тестовые задания по теории вероятностей и математической статистики
Тестовые задания по теории вероятностей и математической статистики
ГБПОУ КК УСПК
ТЕСТОВЫЕ ЗАДАНИЯ ПО ТЕОРИИ ВЕРОЯНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Разработчик: Михайленко И. Д.
г. Усть - Лабинск
2016 г.
1.Комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения, это -
-
сочетания;
-
перестановки;
-
размещения;
4)размещения с повторениями.
2.Комбинации, составленные из n различных элементов по m, которые отличаются либо составом элементов, либо их порядком, это-
1) сочетания;
2) перестановки;
3) размещения;
-
размещения с повторениями.
3. Комбинации, составленные из n различных элементов по m, которые отличаются хотя бы одним элементом, это-
1) сочетания;
2) перестановки;
3) размещения;
4)сочетания с повторениями.
4.В классе учится 17 мальчиков и 19 девочек. Сколькими способами можно назначить одного дежурного?
-
17;
-
19;
-
36;
-
1.
5.Сколько различных смешанных пар для игры в теннис можно образовать из 8 юношей и 6 девушек?
1)8;
2)48;
3)6;
4)14.
6.Расписание одного дня содержит 5 различных уроков. Определить количество таких расписаний одного дня при выборе из 11 дисциплин.
1)А
;
2)С;
3)5!;
4) 11!
7. Для дежурства с понедельника по субботу выделено 6 студентов из группы. Староста группы должен составить график дежурства. Сколькими способами он может это сделать?
1)6;
2)1;
3)120;
4)720.
8.Студенческая группа состоит из 25 человек. Нужно выбрать 3 делегатов на профсоюзную конференцию. Сколькими способами это можно сделать?
1) 
;
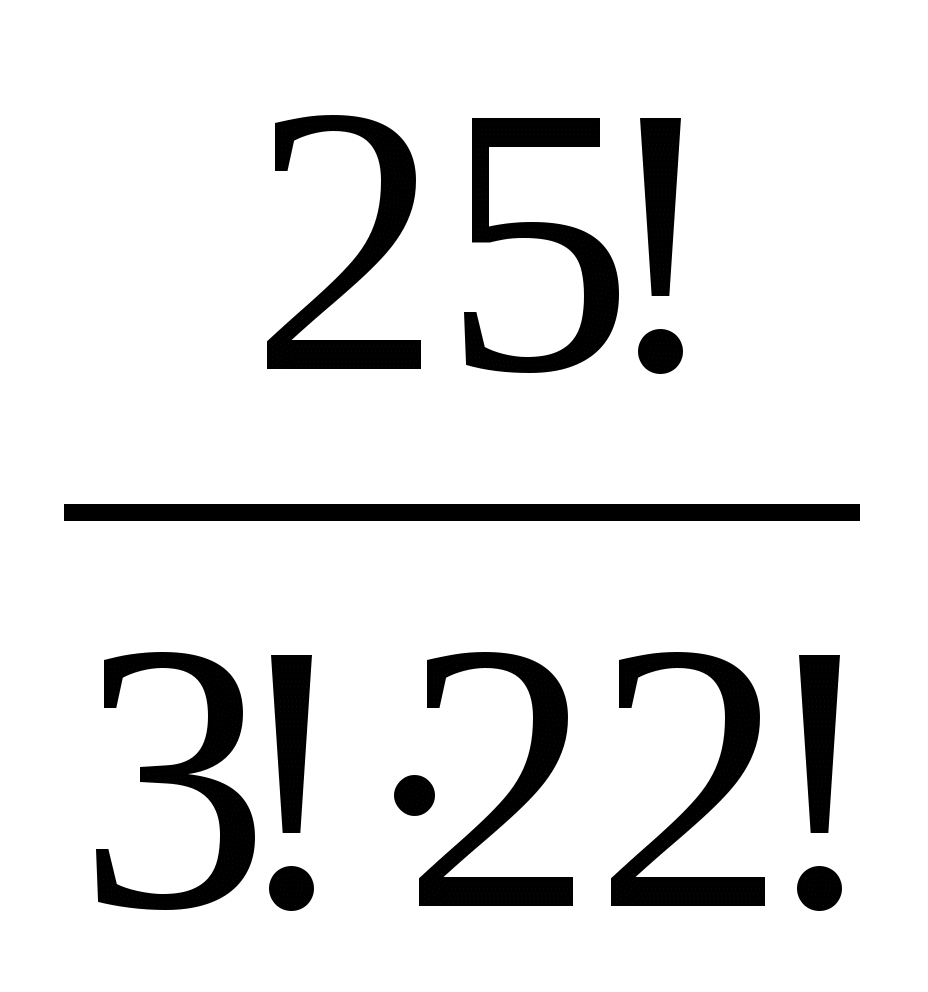2)25!;
3)
;
4) 
.
9.Комиссия состоит из председателя, его заместителя и еще 5 человек- членов комиссии. Сколькими способами 7 человек, избранных в комиссию, могут распределить между собой обязанности?
1)7;
2)6;
3)42;
4)5!.
10.Сколько существует перестановок цифр 0,1,2,3,4,5,6,7,8,9, в которых цифра 0 занимает третье место, цифра 4- пятое место, цифра 7 - седьмое место?
1)10!;
2)7!;
3)9!;
4)8!
11.Чемодан имеет цифровой замок, состоящий из 6 дисков. Сколько различных комбинаций может быть зашифровано?
1)6!;
2)1000000;
3)100;
4)1.
12.В урне 20 шаров с номерами от 1 до 20. Какова вероятность вынуть шар с номером 37?
1) 
;
2) 
;
3) 0;
4) 1.
13. Какова вероятность того, что при случайном расположении кубиков, на которые нанесены буквы О, О, К, К, Э, Н, М, И, А, получится слово «экономика»?
1)
;
2) 
3) 
4) 
14.В ящике лежат 15 красных, 9 синих, 6 зеленых шаров. Наудачу вынимают 6 шаров. Какова вероятность того, что взяты 1 зеленый, 2 синих и 3 красных шара?
1) 
;
2) 
;
3) 
;
4)
.
15. Восемь различных книг расставляются наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом.
1) 
;
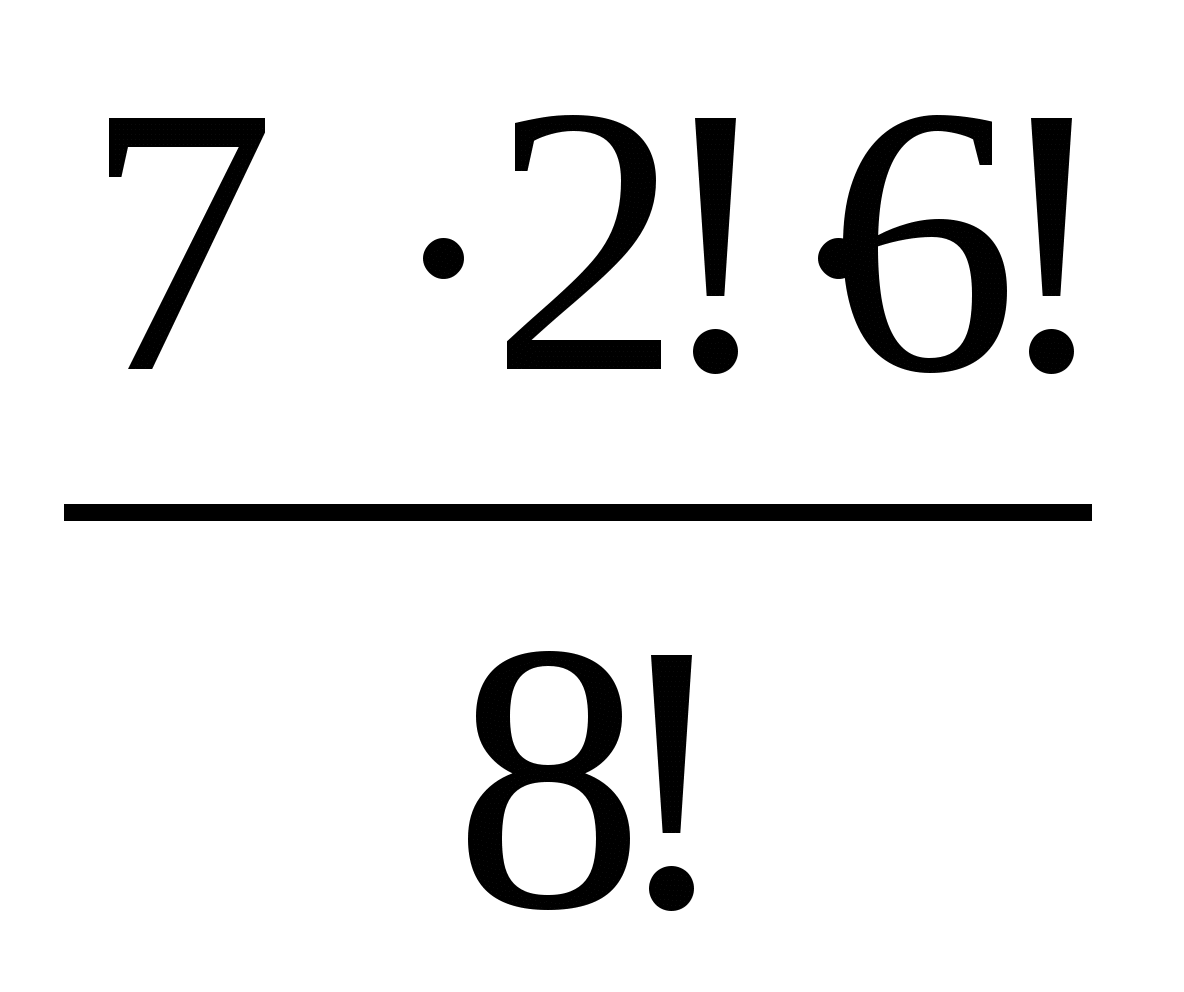2) 
;
3) 
;
4) 
.
16.В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.
1) 
;
2) 
;
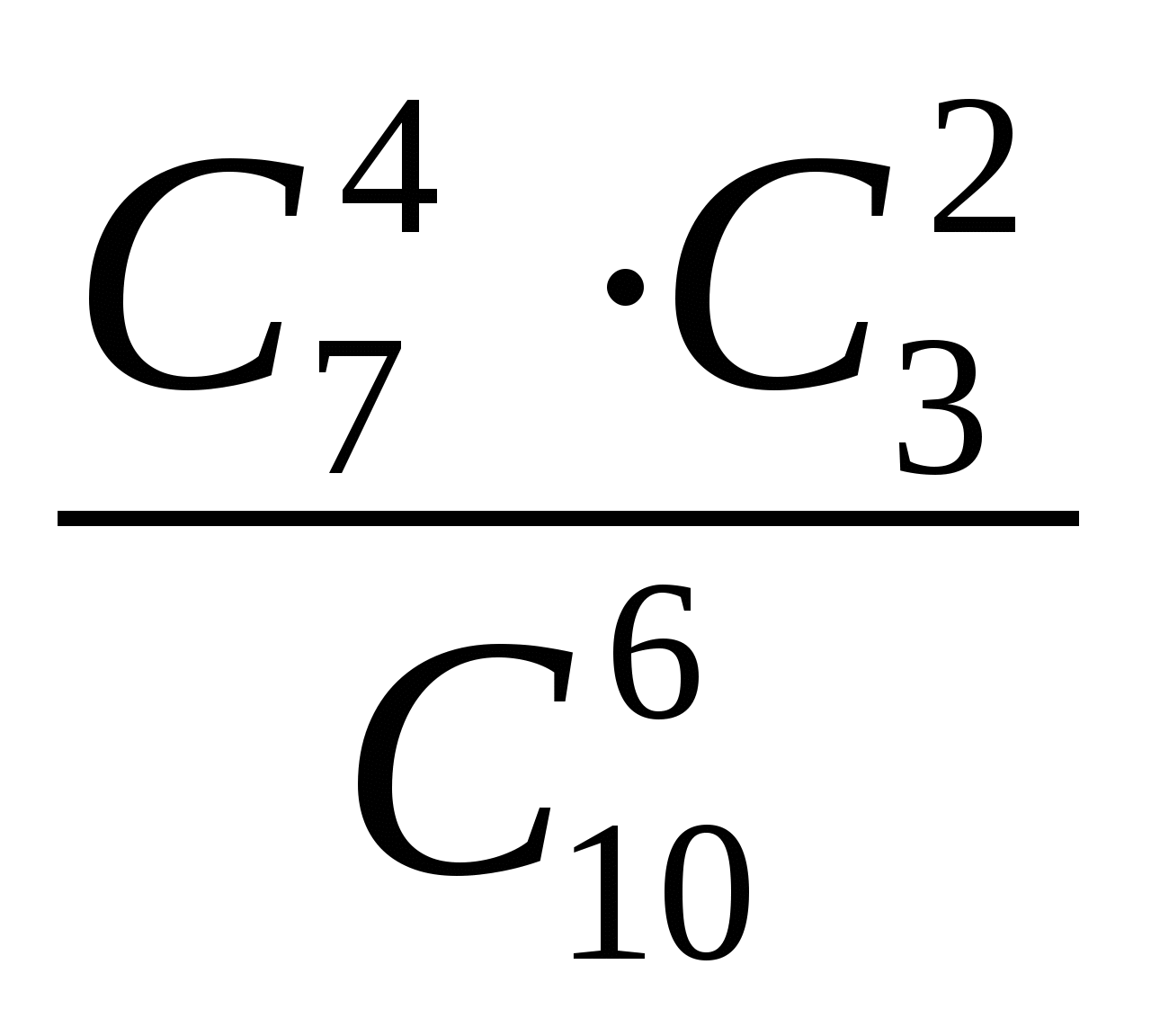3) 
;
4) 
.
17.В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей?
1)0,1;
2) 0,5;
3)0,05;
4)0,2.
18.На плоскости начерчены две концентрические окружности, радиусы которых 10 см и 5 см. Найдите вероятность того, что точка, брошенная наудачу в большой круг, попадет в меньший круг.
1) р=
;
2) р=
;
3) р=
;
4)р=1.
19.В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
1)0,5;
2)0,2;
3) 
;
4) 
.
20.События А,В,С, и D образуют полную группу. Вероятности событий таковы: Р(А)=0,1; Р(В)+0,4; Р(С)=0,3. Чему равна вероятность события D?
1) 0,5;
2) 0;
3) 1;
4) 0,2.
21. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием равна 0,8, а вторым - 0,7.
1) 0,56;
2) 0,7;
3) 0,8;
4) 0,15.
22.Событие А
состоит
в том, что студент сдаст первый экзамен, событие А
-
студент сдаст второй экзамен, событие А
-
студент сдаст второй экзамен. Укажите формулу для нахождения
вероятности сдачи студентом только одного экзамена.
1) Р(
)Р(
)Р(
)
2) Р(
)Р()Р()
3) Р()Р(
)Р(
)+Р()Р()Р()+Р()Р(
)Р();
4) Р ()Р()Р()
23.В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность извлечения черного шара при втором испытании при условии, что в первом испытании был извлечен белый шар.
1) 
2)
;
3) 
4) 1.
24. При включении зажигания двигатель начнет работать с вероятностью р .
Найти вероятность того, что двигатель начнет работать при третьем включении зажигания.
1)
;
2) 
;
3) 
;
4) 
25. Вероятности своевременного выполнения задания тремя
независимо работающими предприятиями соответственно равны 
,
,
.
Найти вероятность своевременного выполнения задания хотя бы одним
предприятием.
1) 
;
2) 
;
3) 
;
4) 
+
+
.
26. Имеется два набора деталей. Вероятность того, что деталь
первого набора стандартна, равна
, а второго -.
Найти вероятность того, что наудачу взятая деталь - стандартная.
-
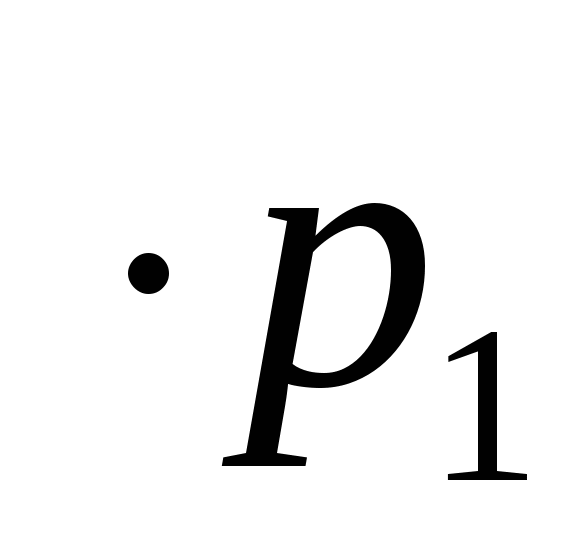0,5
+0,5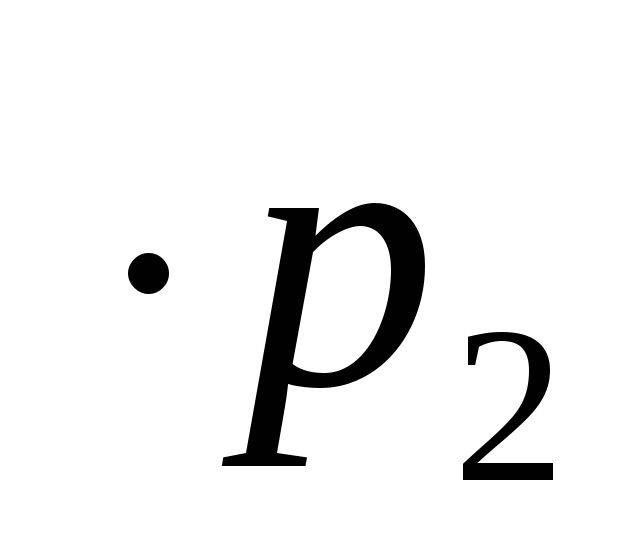
;
-
;
-
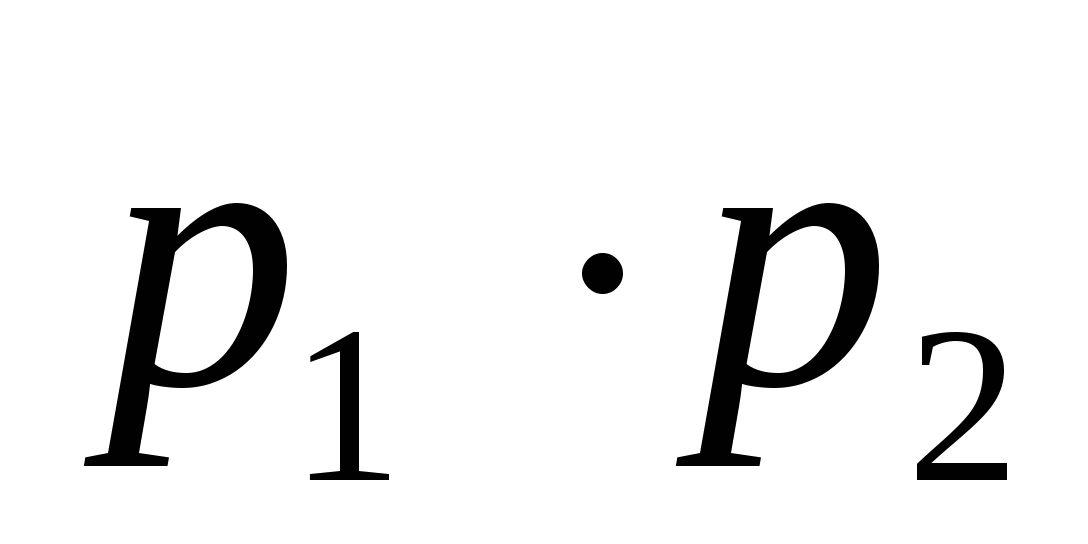0,5
;
-
.
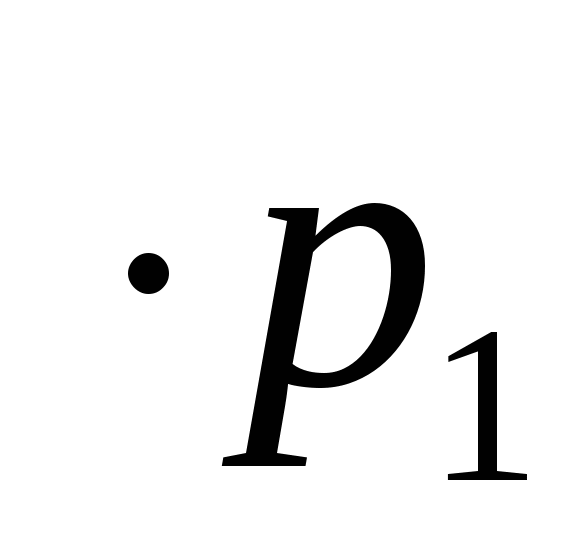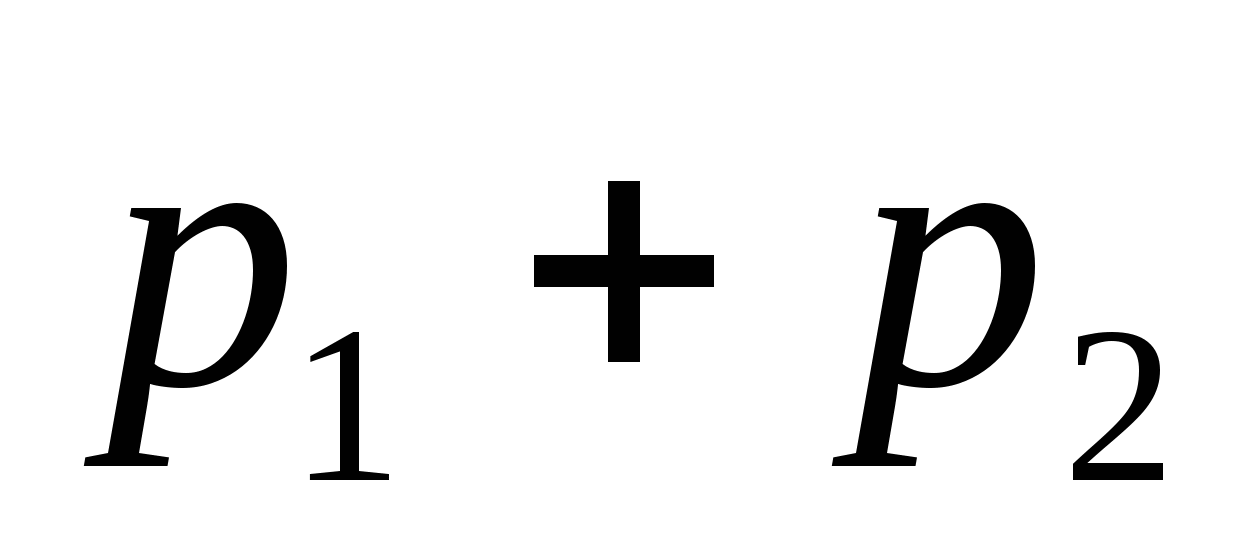27.В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент включено 4 мотора.
1)
;
2) 
;
3) 
;
4) 
.
28.В классе 20 мальчиков и 10 девочек. На каждый из трех вопросов, заданных учителем, ответили по одному ученику. Какова вероятность того, что среди ответивших было два мальчика и одна девочка?
1) 
;
2) 
;
3) 
;
4) 
.
29. Наивероятнейшее число m
наступлений события А в n независимых испытаниях определяется
неравенством:
1)
;
2) 
;
3) 
;
4) 
;
30. По каналу связи передается 1000 знаков. Каждый знак может быть искажен независимо от остальных с вероятностью 0,005. Найти вероятность того, что будет искажено не более 3-х знаков.
1) 1;
2) 
;
3) 
;
4)
.
31. Из урны, содержащей 1 белый и 4 черных шара,
по схеме случайного выбора с возвращением проводят 2500 извлечений
шаров. Найти вероятность того, что число появлений белого шара
между 480 и 540. Результат выразите через функцию Ф(х)=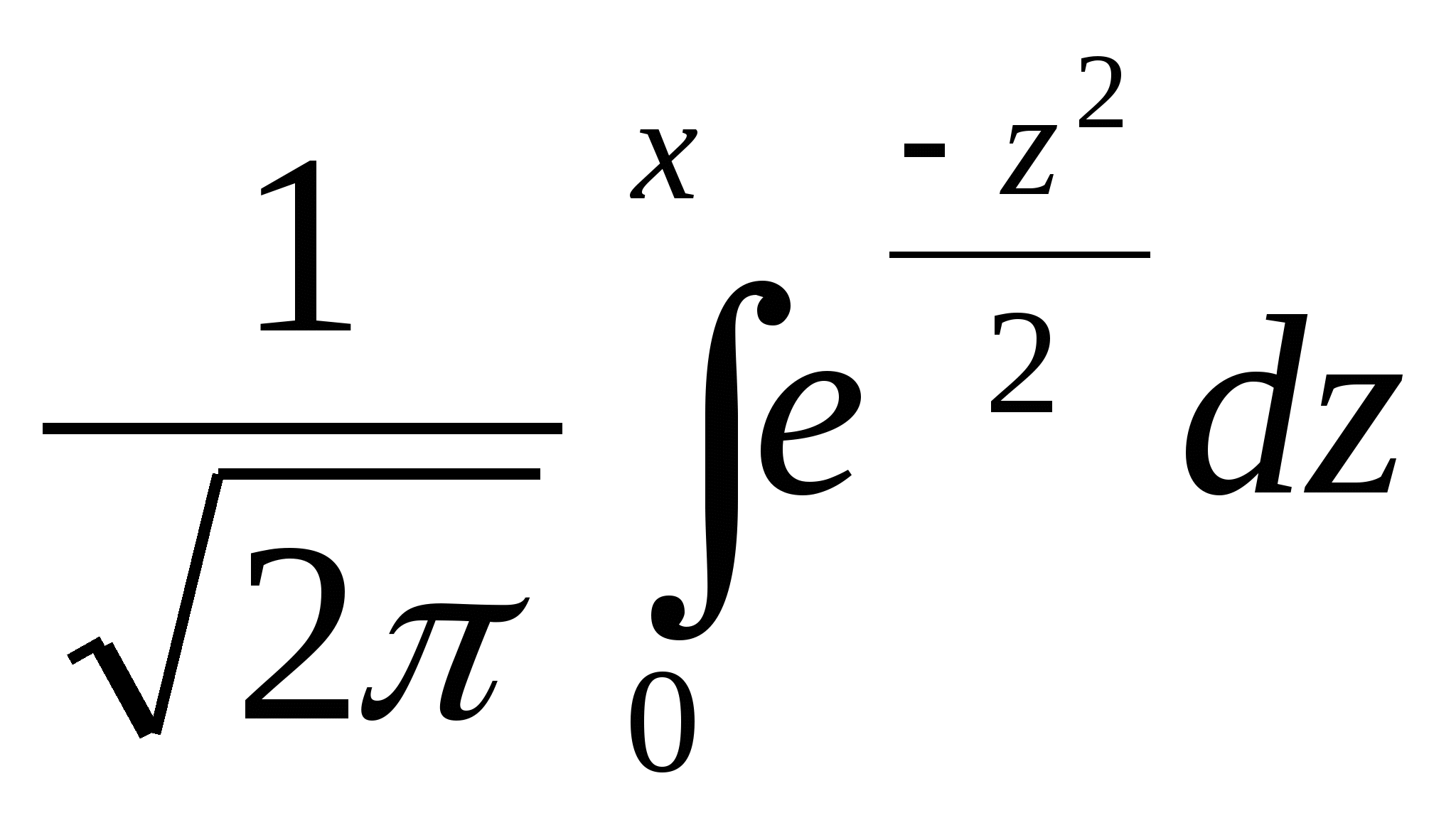
1) Ф(2)+Ф(1);
2) Ф(2)-Ф(1);
3) Ф(2);
4)Ф(1).
32. Укажите свойство, которым не обладает функция Лапласа
Ф (х)=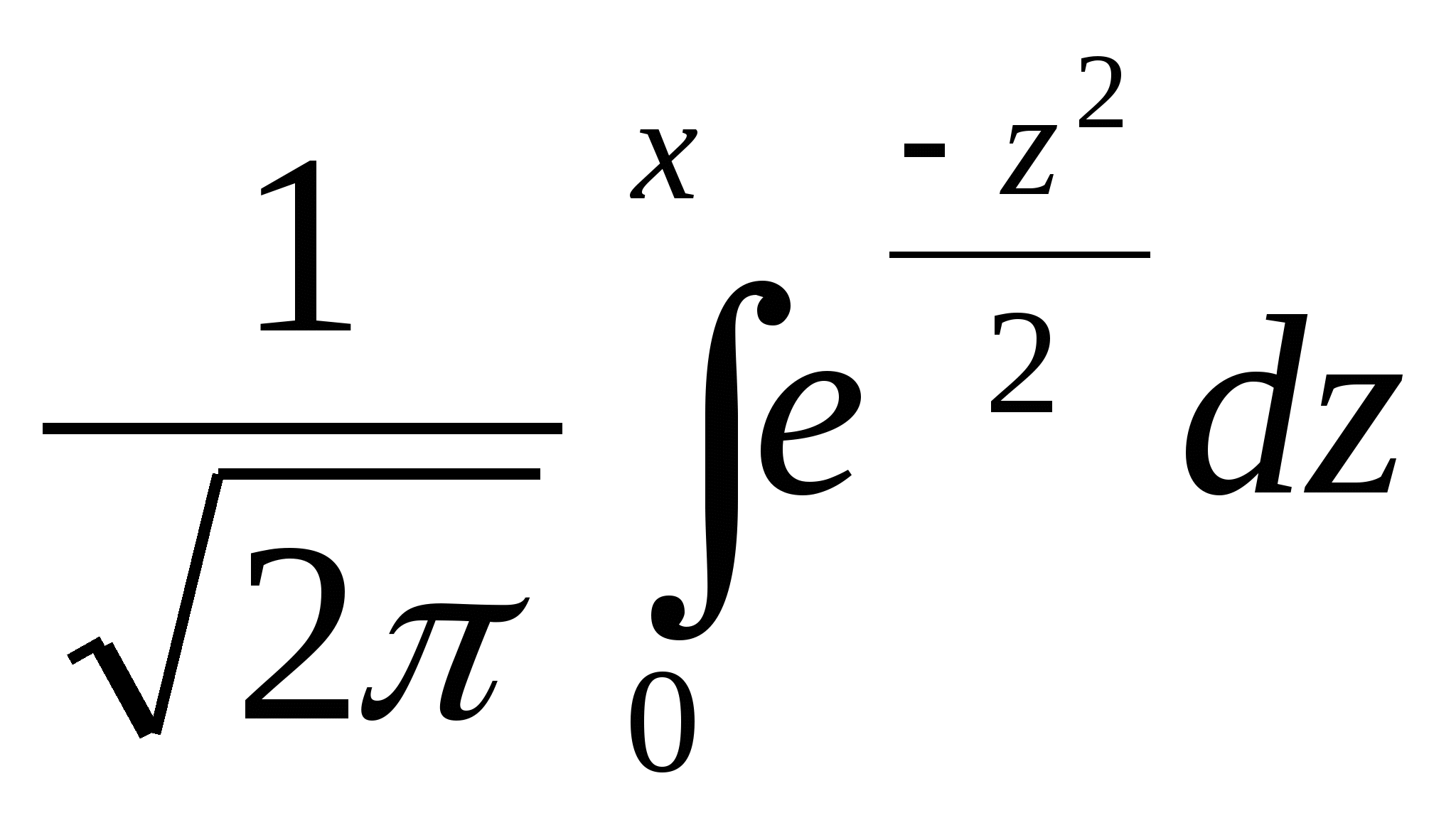
.
1) нечетная;
2) монотонно возрастающая;
3) четная;
4) при 
Ф(х) 
0,5.
33. Известно, что 
рабочих завода имеют среднее образование. Для некоторого
исследования наудачу выбираются 150 человек. Найти вероятность
того, что 93 человека из них имеют среднее образование. Результат
выразите через функцию f(х)=
-
f(0,5);
-
f(1);
3) f(0,4);
4)f(0);
34.Укажите свойство, которым не обладает функция
f(х)=.
1) четная;
2) монотонно убывающая;
3) монотонно возрастающая;
4) при
f(х)
0.
35.В денежной лотерее выпущено100 билетов. Разыгрывается 1 выигрыш 5000р. и 10 выигрышей по 100р. Найдите закон распределения случайного выигрыша Х для владельца одного лотерейного билета.
1)
-
Х
0
100
5000
Р
0,89
0,1
0,01
2)
-
Х
1
2
3
Р
0,89
0,1
0,01
3)
-
Х
100
5000
Р
0,1
0,01
4)
-
Х
0
100
5000
Р
0,11
0,1
0,01
36.Закон распределения случайной величины Х задан таблицей
-
Найдите р.
1) 1;
2) 0,6;
3) 0,5;
4) 0.
37.Сумма произведений всех возможных значений дискретной случайной величины Х на соответствующие вероятности называется
-
дисперсией дискретной случайной величины Х;
-
математическим ожиданием дискретной случайной величины Х;
-
средним квадратичным отклонением дискретной случайной величины Х;
4) центральным моментом порядка k.
38. Найти математическое ожидание случайной величины Z=Х+2Y, если М(Х)=5, М(Y)=3.
1)5
2)3
3)11
4)17
39.Найти математическое ожидание случайной величины Z=ХY, если М(Х)=1,5. М(Y)=2.
1)1,5;
2)2;
3)3;
4)3,5.
40.Математическое ожидание отклонения случайной величины Х от математического ожидания равно:
-
M(Х);
-
D(Х);
-
1;
-
0.
41.Математическое ожидание квадрата отклонения дискретной случайной величины Х от ее математического ожидания называется:
-
средним квадратичным отклонением;
-
дисперсией дискретной случайной величины;
-
начальным моментом порядка k;
-
математическим ожиданием.
42.Дисперсия случайной величины Х равна 6,25. Найдите среднее квадратичное отклонение.
1)6,25
2)2,5
3)3,25
4)1.
43.Начальный момент второго порядка равен:
-
М(Х);
-
М(Х
);
-
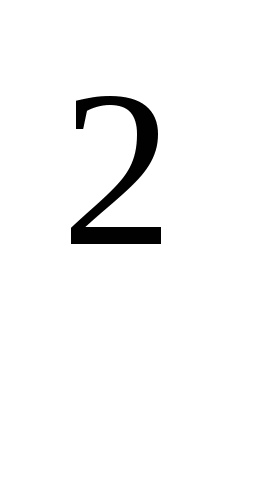D(Х);
-
0
44.Дисперсия случайной величины Х равна 3. Найдите дисперсию случайной величины Z=4Х+3.
1) 48
2 )12;
3) 16;
4) 0.
45.Случайная величина Х задана функцией распределения
F(Х)=
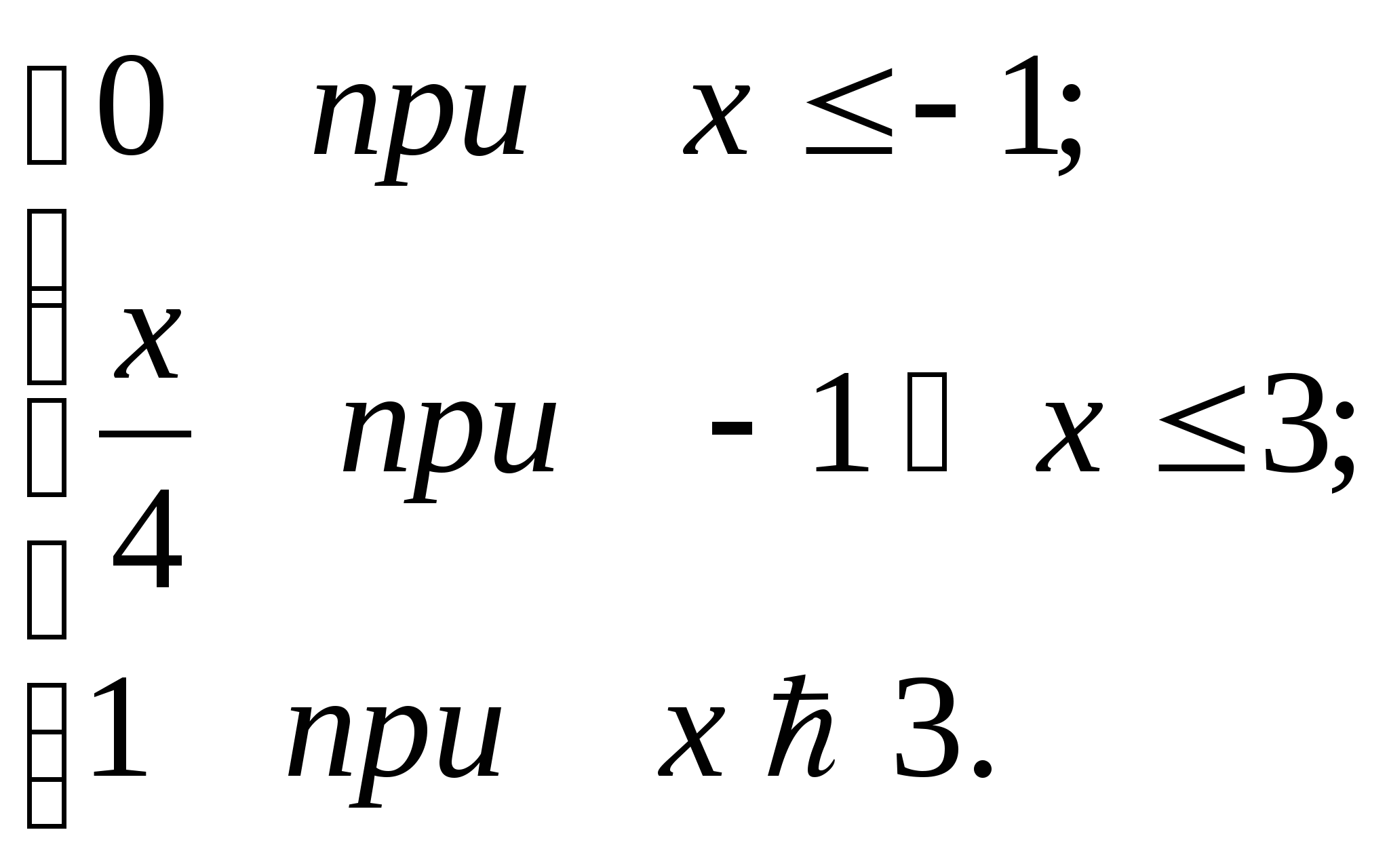
Найти вероятность попадания случайной величины в интервал (0;2)
1)1,25
2)0,5
3)1;
4)0.
46.Задана плотность вероятности случайной величины Х:
f(x)=
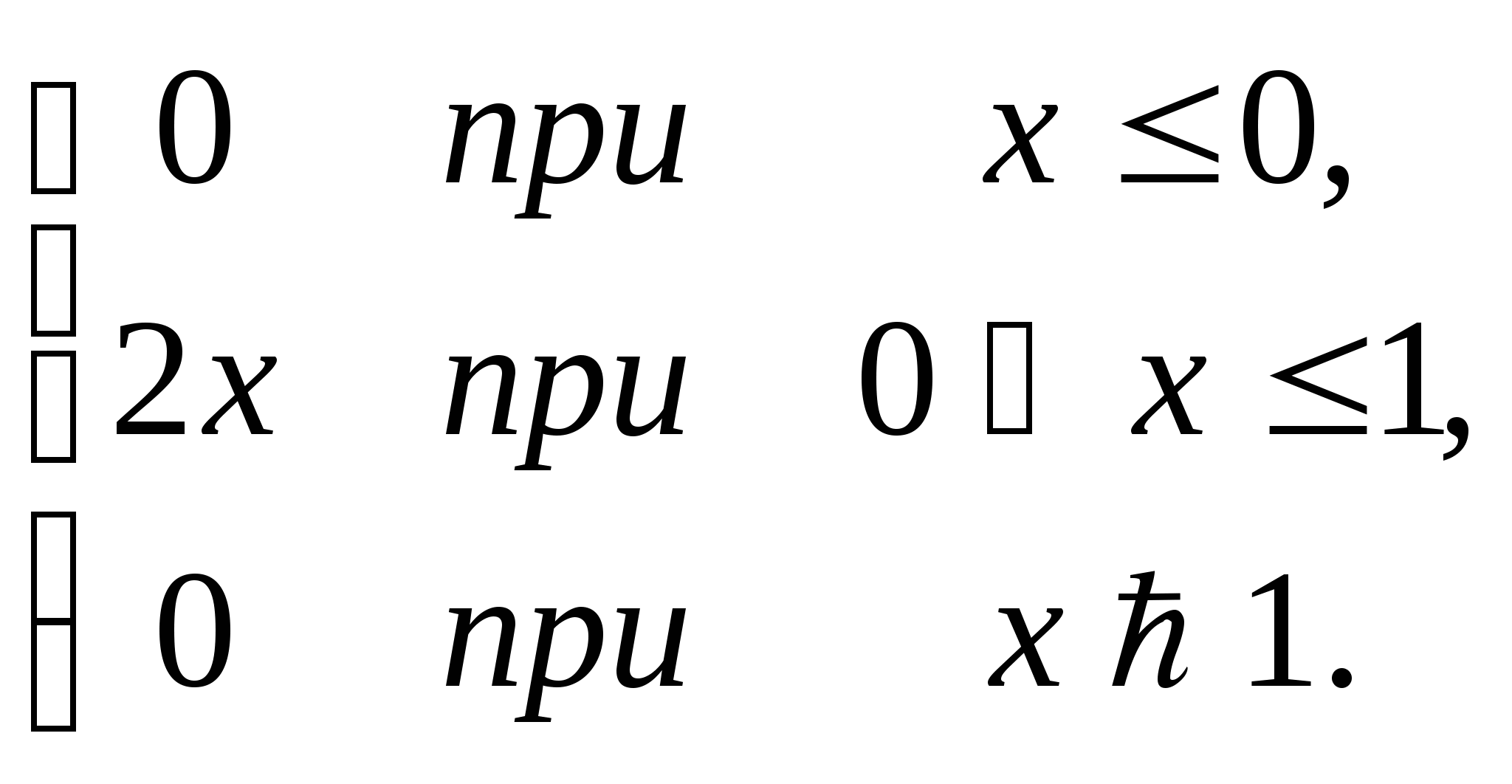
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5;1).
1 )1;
2 )0,75;
3) 0,25;
4) 0.
47.Найти математическое ожидание случайной величины Х, заданной плотностью вероятности:
f(x)=
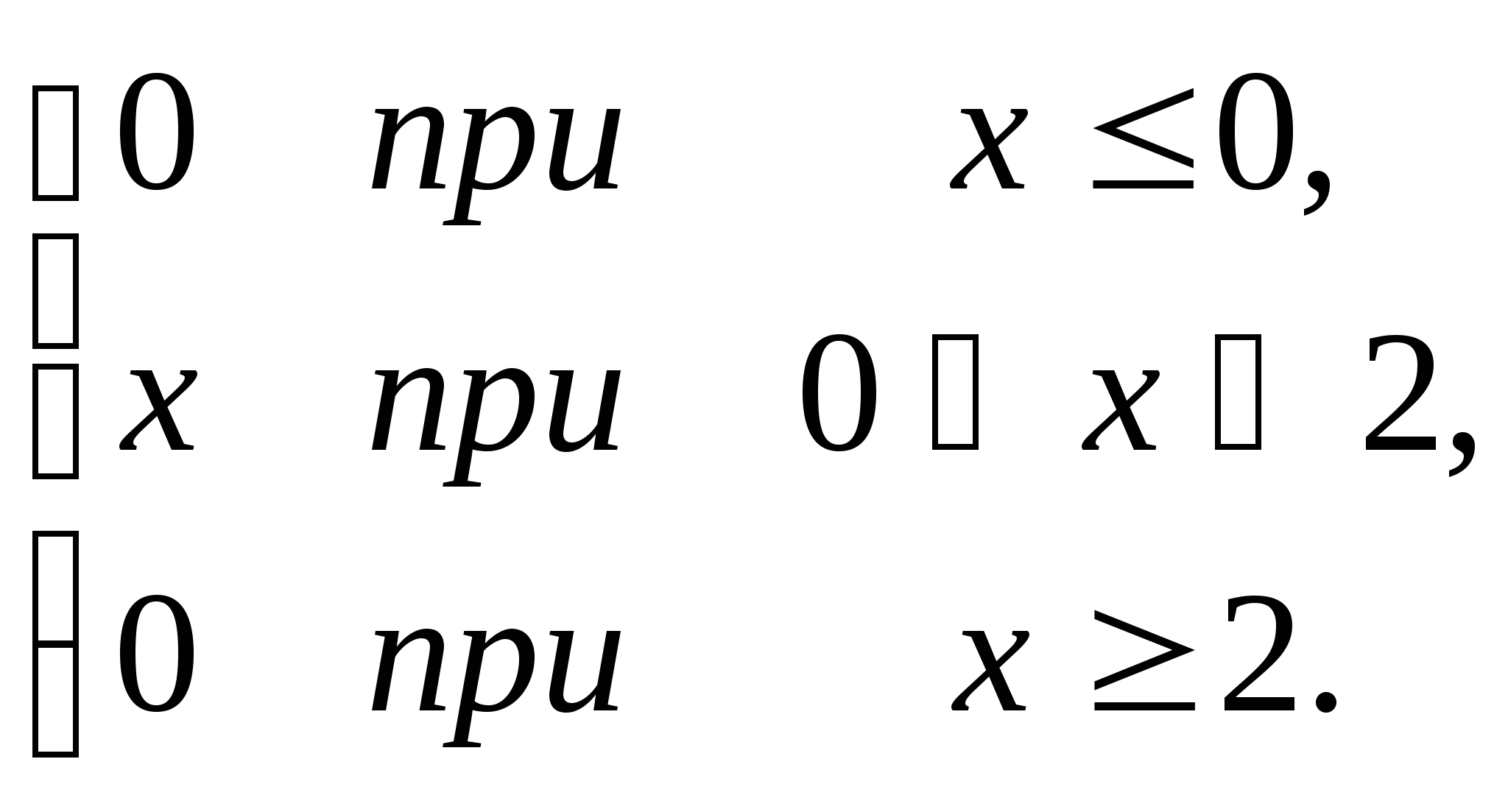
1)
;
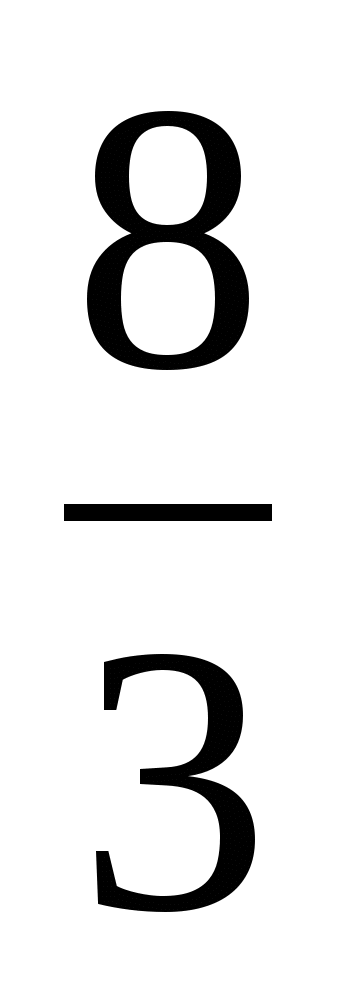2)
;
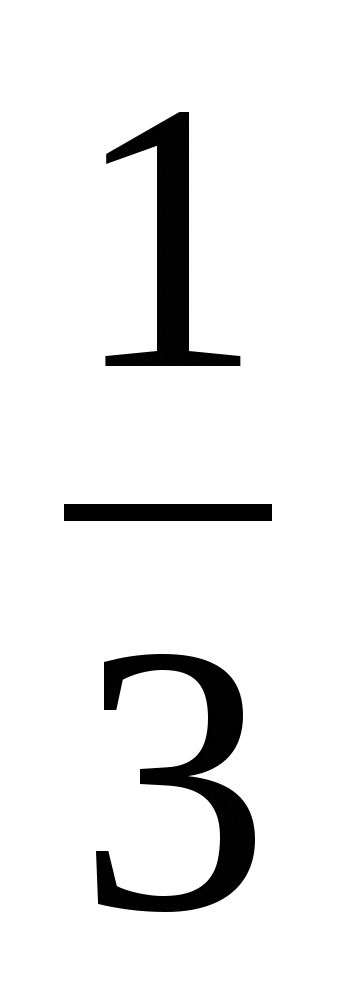3) 1;
4) 0,5.
48.Найти дисперсию случайной величины Х - числа появлений события в 100 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,7
-
70;
-
21;
-
30;
-
1.
49.Случайная величина Х распределена равномерно на отрезке [1;6]. Найти математическое ожидание М(Х).
-
М (Х)=3,5;
-
М (Х)=0,5;
-
М (Х)=1;
-
М(Х)=2,5.
50. Математическое ожидание и среднее квадратичное отклонение нормально распределенной случайной величины Х соответственно равны 12 и 2. Найти вероятность того, что случайная величина примет значение, заключенное в интервале (14;16). Результат выразите через функцию Лапласа Ф(Х)=
-
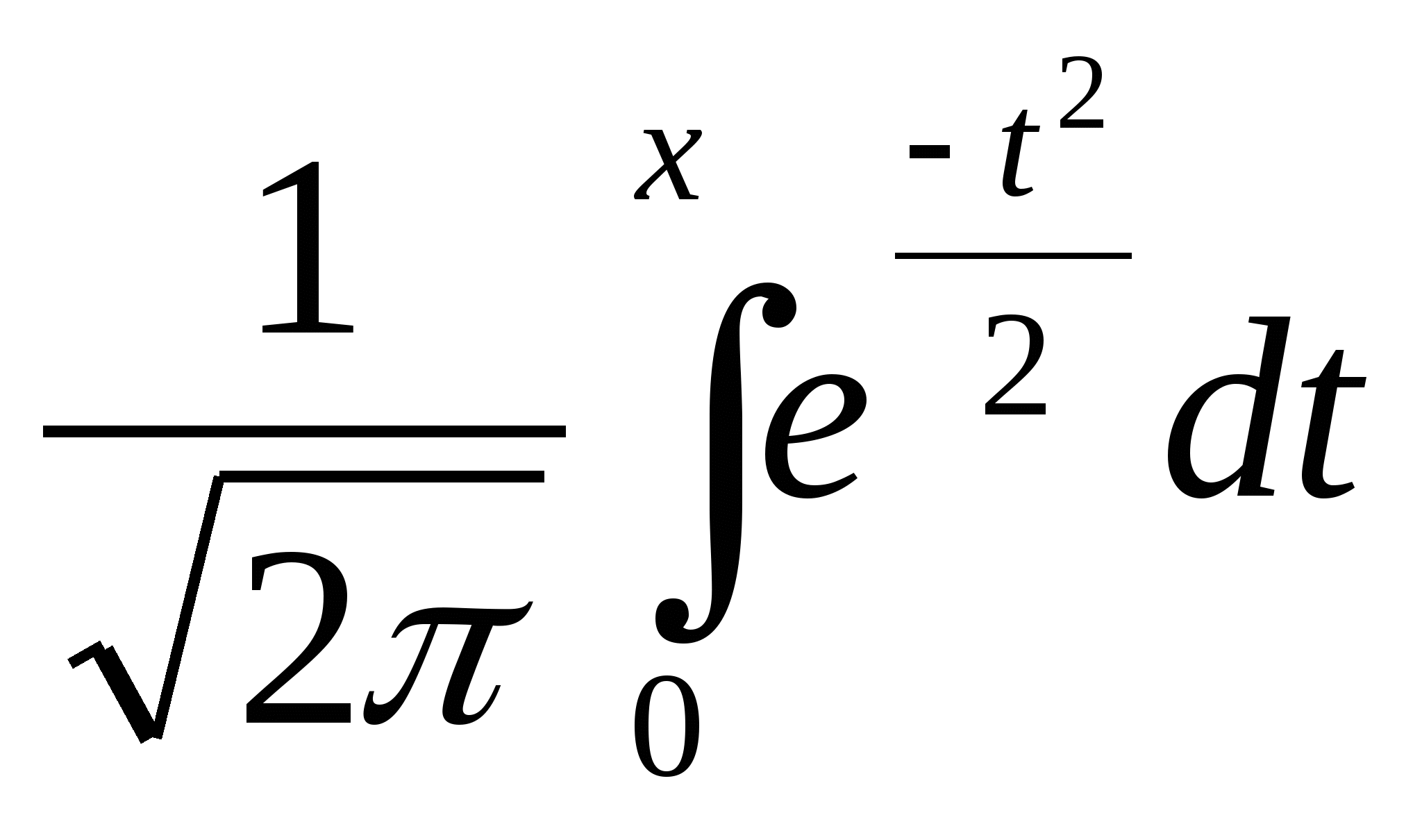
Ф(2)+Ф(1);
-
Ф(2)-Ф(1);
-
Ф(2);
-
Ф(1).
51. Непрерывная случайная величина Х распределена по показательному закону
f(x)=
.
Найти математическое ожидание М(Х), дисперсию D(Х) и среднее квадратичное отклонение
(Х).
-
М(Х)=0,2; D(Х)=0,04;
(Х)=0,04;
-
М(Х)=0,2; D(Х)=0,2;
(Х)=0,04;
-
М(Х)=0,2; D(Х)=0,04;
(Х)=0,2;
-
М(Х)=0,5; D(Х)=0,2;
(Х)=0,5.
52. Статистическая совокупность, из которой отбирают часть объектов - это:
-
Выборка;
-
Генеральная совокупность;
-
Полигон частот;
-
Гистограмма частот.
53. Среднее арифметическое значений признака генеральной совокупности - это:
-
Генеральная средняя;
-
Выборочная средняя;
-
Генеральная дисперсия;
-
Выборочная дисперсия.
54. Среднее арифметическое значений признака выборочной совокупности - это:
-
Генеральная средняя;
-
Выборочная средняя;
-
Генеральная дисперсия;
-
Выборочная дисперсия.
55. Среднее арифметическое квадратов отклонений значений признака генеральной совокупности от генеральной средней - это:
1) Генеральная средняя;
2) Выборочная средняя;
3) Генеральная дисперсия;
4) Выборочная дисперсия.
56. Среднее арифметическое квадратов отклонений наблюдаемых значений признака от выборочной средней - это:
1) Генеральная средняя;
2) Выборочная средняя;
3) Генеральная дисперсия;
4) Выборочная дисперсия.
57. Статистическая оценка, математическое ожидание которой равно оцениваемому параметру, называется:
-
Несмещенной;
-
Смещенной;
-
Состоятельной;
-
Эффективной.
58. Статистическая оценка, математическое ожидание которой не рано оцениваемому параметру, называется:
-
Несмещенной;
-
Смещенной;
-
Состоятельной;
-
Эффективной.
59. Статистическая оценка, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию называется:
-
Несмещенной;
2) Смещенной;
3) Состоятельной;
4)Эффективной.
60. Статистическая оценка, которая при n
стремится по вероятности к оцениваемому параметру, называется:
-
Несмещенной;
2) Смещенной;
3) Состоятельной;
4)Эффективной.
Ответы
вопроса№ правильного ответа
№ вопроса
№ правильного ответа
1
2
31
1
2
3
32
3
3
1
33
1
4
3
34
3
5
2
35
1
6
1
36
3
7
4
37
2
8
1
38
3
9
3
39
3
10
2
40
4
11
2
41
2
12
3
42
2
13
1
43
2
14
4
44
1
15
1
45
2
16
2
46
2
17
3
47
1
18
2
48
2
19
1
49
1
20
4
50
2
21
1
51
3
22
3
52
2
23
2
53
1
24
2
54
2
25
3
55
3
26
1
56
4
27
1
57
1
28
2
58
2
29
2
59
4
30
4
60
3
-