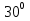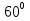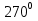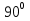- Учителю
- конспект урока алгебры Обобщение темы «Тригонометрические функции», 10 класс
конспект урока алгебры Обобщение темы «Тригонометрические функции», 10 класс
| Четверть II | Неделя 12 | День 19.11.2014 | Предмет: алгебра | Урок 31 | 10 «Б» класс | ||||||
| Тема урока: | Обобщение темы «Тригонометрические функции» | ||||||||||
| Цель:
| Обобщение и систематизация знаний по темам тригонометрические функции и обратные тригонометрические функции | ||||||||||
| Результат обучения для ученика А: | Учащиеся будут знать: - виды тригонометрических функций и обратных тригонометрических функций - свойства тригонометрических функций - значение тригонометрических функций для углов 00, 300,450, 600,900 ; таблицу значений обратных тригонометрических функций | ||||||||||
| Результат обучения для ученика Б: | Учащиеся будут знать: - виды тригонометрических функций и обратных тригонометрических функций - свойства тригонометрических функций - значение тригонометрических функций для углов 00, 300,450, 600,900 ; таблицу значений обратных тригонометрических функций - отличительные свойства графиков тригонометрических функций Учащиеся будут уметь: - строить графики тригонометрических функций | ||||||||||
| Результат обучения для ученика В: | Учащиеся будут знать: - виды тригонометрических функций и обратных тригонометрических функций - свойства тригонометрических функций - значение тригонометрических функций для углов 00, 300,450, 600,900 ; таблицу значений обратных тригонометрических функций - отличительные свойства графиков тригонометрических функций Учащиеся будут уметь: - строить и читать графики тригонометрических функций, обратных тригонометрических функций | ||||||||||
| Основные ключевые идеи:
| Тригонометрические функции: синус, косинус, тангенс и котангенс; обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккатангенс. Свойства, графики функций. Преобразование графиков функции. Алгоритм исследования функций
| ||||||||||
| Вид деятельности | Время | Деятельность учителя | Деятельность ученика | ||||||||
| Вводно-мотивационный этап |
3 мин
| Проводит разминку, в ходе которой формируются 3 группы учащихся. | Организуют рабочее место, выбирают лидера группы | ||||||||
| Этап актуализации знаний. (исторические сведения) | 7 мин
| Организует беседу «Гений состоит из 1% вдохновения и 99% потения».(Эдисон) Я надеюсь, что каждый из вас сложил в подготовку 99% потения.
Ответ: слово «тригонометрия» впервые встречается в 1505 году в заглавии книги немецкого теолога и математика Питискуса. Происхождение этого слова греческое: « trigonon»- треугольник, «metrio» -мера. Иными словами, тригонометрия - наука об измерении треугольников.
Для того чтобы ответить на этот вопрос вы должны заполнить таблицу. Выразить в радианной мере величины углов. |
|
|
|
| |||||
|
|
|
|
|
| |||||||
Ответ: Леонард Эйлер (на экране показан слайд с фотографией и биографией Эйлера).
Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношение сторон в прямоугольном треугольнике, которые по существу и есть тригонометрические функции, встречаются уже в III в.до н.э. в работах Евклида, Архимеда, Аполлония Пергского и др. Имея дело тригонометрическими функциями, мы существенно выходим за рамки задачи «измерения треугольников». Поэтому известный математик Ф. Клейн предлагал учение о «тригонометрических функциях» назвать иначе - гониометрией (лат. «гонио» означает «угол»). Однако это название не прижилось. (приложение 1)
Участвуют в беседе, дают ответы на вопросы, работают на листах - заготовках
Разминка
5 мин
Командам предлагаются графики функции. По которым необходимо определить какие преобразования графика произведены и график какой функции построен. (приложение 2)
Участвуют в обсуждении полученных графиков, выбирают правильный ответ
«Найди ошибку»
5 мин
« У математиков существует свой язык - формулы». (С. Ковалевская)
Командам дают задания и ответ, необходимо найти ошибку.
-
sin π=
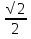 5) arcsin
5) arcsin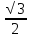 =
= 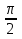 9) arcsin1 = 1
9) arcsin1 = 1 -
cos
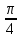 =
= 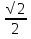 6)arсcos(-
6)arсcos(- 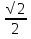 )=
)= 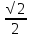 10) cos π = 0
10) cos π = 0 -
tg
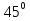 = 1 7) arctg
= 1 7) arctg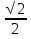 =
= 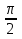 11) sin
11) sin 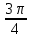 =
= 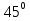
-
ctg
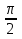 = -1 8) arcctg
= -1 8) arcctg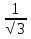 = 0 12) tg
= 0 12) tg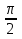 = 0
= 0
Группой находят все допущенные ошибки.
Взаимопроверка по образцу, выставление баллов в лист ответов.
«Байга»
10 мин
Учащимся задаются вопросы, на которые они должны тут же ответить.
«Математику нельзя изучать, наблюдая, как это делает сосед»(А. Нивен )
-
Область определения функции y=sinx, y= cosx.
-
Верно ли, что для любого х справедливо равенство sin(-x)= -sinx ?
-
Наименьший положительный период функции y= sinx, y=cosx равен…
-
Где и когда был введен термин «радиан»? (Англия 1873 г.)
-
Знак синуса во 2-ой четверти.
-
Область значения функции y= sin х, y=cosx.
-
Назовите четвертные тригонометрические функции.
-
Верно ли, что график функции y= sin х симметричен относительно оси ординат?
-
Что означает слово «тригонометрия»? (наука об измерении треугольника)
-
Знак тангенса в 3 четверти.
-
Кто придал современный вид тригонометрии, ввел определение тригонометрических функций, формулы приведения? (Эйлер)
-
Верно ли, что график функции y=cosx- четная?
-
Чему равно
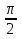 в градусной мере?
в градусной мере? -
Верно ли, что график функцииy=cosx симметричен относительно начала координат?
-
Область значения функции tgx, ctgx.
Устная фронтальная работа
За каждый правильный ответ жетон группе. По окончании подсчет жетонов, занесение результатов в лист ответов
«Великолепная тройка»
10-12 мин
Объясняет условия конкурса, правила его проведения.
«Математика - наука молодых, иначе быть не может, занятие математикой это такая гимнастика для ума, для которой нужны вся гибкость и выносливость молодости». (Винер)
В этом туре вам будут предложены разные вопросы, которые зависят от уровня сложности и темы.
История
«3»
«4»
«5»
Теория
«3»
«4»
«5»
Практика
«3»
«4»
«5»
История:
1)От какого латинского слова произошло слово «радиан»? (radius-спица, луч)
2)Кто из математиков XIIIв., швейцарец по происхождению, долгие годы работал в Росии и являлся членом Петербургской АН? (Эйлер)
3)Какая тригонометрическая функция возникла в результате решения задач на определение длины теней?(тангенс)
Теория:
1)Как переводится с латинского на русский слово «синус»? (изгиб)
2)Что означает асимптоты при построении графиков функции tgx, ctgx.
3)Сколько ходов нужно сделать, чтобы построить график функции f(x) = 1+2 cos (x - 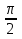 ) (4 шага)
) (4 шага)
Практика:
1)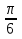 x +
x + 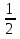 x = (единице)
x = (единице)
2)Найдите числовое значение выражения:
8sin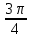 cos
cos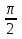 tg
tg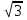 ctg
ctg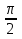 = 4(-
= 4(- 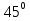 )
)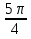 3 (-1) =2
3 (-1) =2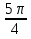 3
3
3)Постройте график функции f(x)=4cos 3x
По очереди выбирают категорию и цену вопроса, на выполнение задания 2-3 минуты. За каждое правильно выполненное задание в лист ответов заносят его цену
Рефлексия
3-5 мин
Учитель проводит беседу по вопросам:
Как мы сегодня поработали?
Узнали ли для себя новое?
Какие виды работ понравились?
Кто сегодня лучше всех работал?
А если такие, которые мы не слышали в течении урока? Какие оценки получили?
Высказывают свое мнение.
Подводят итоги своей работы по оценочному листу, куда заносились в течении урока баллы. Все получили оценки за несколько этапов урока, выводится итоговая.
Ресурсы:
Презентация к уроку. Приложение 1, приложение 2
Домашнее задание:
Глава 3 - повторить
Составить по пять тестовых заданий по обобщенной теме.
Приложение 2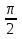
1. График, какой функции изображен на рисунке?
1) y = 1/2 sin x
2) y = 2cos x
3) y = cos 2x
4) y = 2sinx
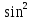
2. График, какой функции изображен на рисунке?
1) y = - sin x
2) y = cos x
3) y = sin x
4) y = - cos x
3. График, какой функции изображен на рисунке?
1) y = - 2cos x
2) y = - 2sin x
3) y = 1/2 cos x
4) y = sin 2x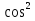
4. График, какой функции изображен на рисунке?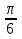
1) y = - cos x
2) y = cos x
3) y = sin x
4) y = - sin x
5. График, какой функции изображен на рисунке?
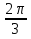
1) y = - cos x
2) y = cos x
3) y = - sin x
4) y = sin x
6. График, какой функции изображен на рисунке?
1) y = - 3 cos x
2) y = - 1/3 sin x
3) y = cos 3x
4) y = 3 sin x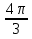
7. График, какой функции изображен на рисунке? 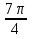
1) y = - cos x
2) y = - sin x
3) y = cos x
4) y = sin x
8. График, какой функции изображен на рисунке?
1) y = - sin 2x
2) y = 1/2 cos x
3) y = 2 sin x
4) y = - 2 cos x
9. График, какой функции изображен на рисунке?
1) y = 3 cos x
2) y = - 3 sin x
3) y = - cos 3x
4) y = 1/3 sin x
10. График, какой функции изображен на рисунке?
1) y = 2 cos x
2) y = - 2 sin x
3) y = - 1/2 cos x
4) y = sin 2x