- Учителю
- Рабочая программа по алгебре , 4ч мордкович
Рабочая программа по алгебре , 4ч мордкович
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №2 с. Новобелокатай муниципального района Белокатайский район Республики Башкортостан
Рабочая программа по алгебре и началам анализа
В 11 классе
химико-биологического и индустриально-технологического профиля
на 2015-2016 учебный год
Учитель: Ртищева И.П.
Рассмотрено и принято Утверждаю:
На заседании педагогического совета Директор МБОУ СОШ №2 с. Новобелокатай
МБОУ СОШ №2 с. Новобелокатай _______________Н.Ф.Минигалина
Протокол «_____»____________2015г.№____ Приказ от «_____» _______________2015г.№_____
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Школьное математическое образование ставит следующие цели обучения:
-
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
-
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
-
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
-
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося и выпускника, виды контроля, а также компьютерное обеспечение урока.
Общая характеристика учебного предмета
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа. В рамках указанных содержательных линий решаются следующие задачи:
1.систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
2.расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
3.развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления.
Программы составлены на основе Государственного стандарта среднего (полного) общего образования по математике. Система уроков условна, но все же выделяются следующие виды:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном так и в компьютерном варианте. Причем в компьютерном варианте всегда с ограничением времени.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются разные виды самостоятельных работ: двухуровневая - уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5»; большой список заданий разного уровня, из которого учащийся решает их по своему выбору.
Урок-контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Применение анимации при создании такого компьютерного продукта позволяет рассматривать вопросы математической теории в движении, обеспечивает другой подход к изучению нового материала, вызывает повышенное внимание и интерес у учащихся.
Изучение многих тем в математике связано с знанием и пониманием свойств элементарных функций. Решение уравнений, неравенств, различных задач предполагает глубокое знание поведения элементарных функций. Научиться распознавать графики таких функций, суметь рассказать об их свойствах помогают компьютерные слайды .
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель - ученик, взаимопроверки, а также в виде тренировочных занятий.
Тренировочные упражнения.
Включают в себя задания с вопросами и наглядными ответами, составленными с помощью анимации. Они позволяют ученику самостоятельно отрабатывать различные вопросы математической теории и практики.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе среднего (полного) общего образования отводится не менее 132 часов из расчета 4 часа в неделю.
Минимальное количество часов преподавания алгебры в 11 классе 2 часа в неделю, оптимальное - 3 часа в неделю .
Учебно - тематический план
Наименование разделов и тем
Всего часов
1
Повторение курса алгебры 10 класса
4
2
Степени и корни. Степенные функции
20
3
Показательная и логарифмическая функция
30
4
Первообразная и интеграл
12
5
Элементы математической статистики, комбинаторики и теории вероятностей
18
6
Уравнения и неравенства. Системы уравнений и неравенств
24
7
Итоговое повторение
24
Итого:
132
ОСНОВНАЯ ЧАСТЬ
Тема 1. «Повторение курса алгебры и начал математического анализа 10 класса» (4 часов)
Раздел математики. Сквозная линия
Числа и вычисления.
Уравнения и неравенства.
Функции.
Обязательный минимум содержания образовательной области математика
-
Числовые и буквенные выражения, преобразования и вычисление их значений.
-
Рациональные уравнения и неравенства и их системы.
-
Функции, их свойства и графики.
-
Производные элементарных функций.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем.
-
Уметь проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы и тригонометрические функции.
Уметь находить производные функций, пользуясь правилами дифференцирования.
Уметь применять производные для исследования функций и построения их графиков в несложных случаях.
Уровень возможной подготовки обучающегося
Освоить технику дифференцирования.
Уметь находить производную сложной функции.
Научиться применять дифференциальное исчисление для исследования элементарных и сложных функций и построения их графиков.
-
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Уровень обязательной подготовки выпускника

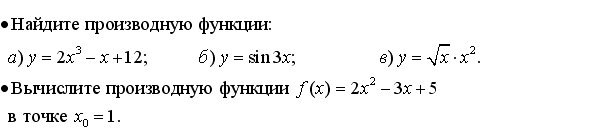
Уровень возможной подготовки выпускника
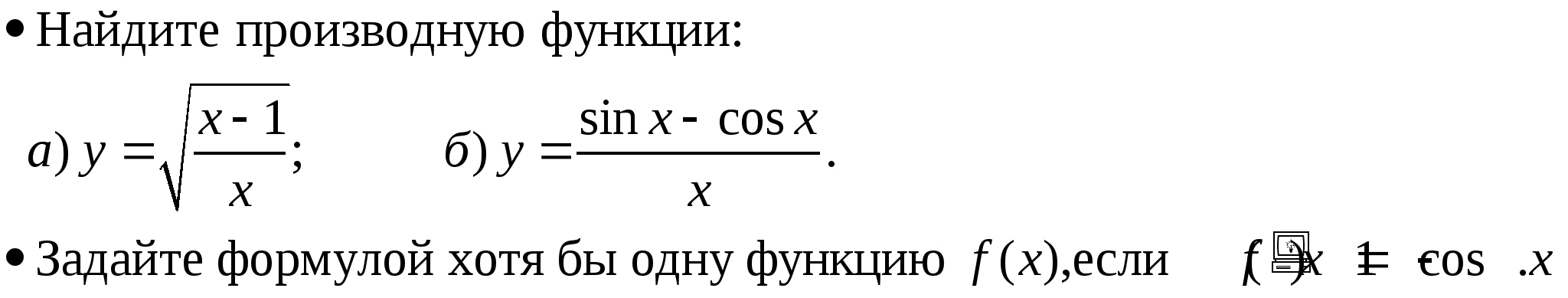
Тема 2. «Степени и корни. Степенная функция» (20 часов)
Раздел математики.
Числа и вычисления
Выражения и преобразования
Уравнения и неравенства
Функции.
Обязательный минимум содержания образовательной области математика
Определение арифметического корня n-й степени, свойства, применение в вычислениях.
Преобразование выражений, содержащих радикалы.
Степенные функции, их свойства и графики.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь выполнять основные действия со степенями с целыми и рациональными показателями.
Уметь применять свойства корня n-й степени для вычисления значений и преобразований числовых выражений, содержащих корни n-й степени.
Знать свойства степенных функций и уметь применять их при решении практических задач.
Уровень возможной подготовки обучающегося
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами.
Уметь выполнять основные действия со степенями с рациональными показателями.
Уметь применять на практике многообразие свойств и графиков степенной функции в зависимости от значений оснований и показателей степени.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Тема 3. «Показательная и логарифмическая функции»
(30 часов)
Раздел математики.
Вычисления и преобразования
Функции
Уравнения и неравенства
Обязательный минимум содержания образовательной области математика
Показательная функция и ее свойства и график.
Показательные уравнения и неравенства и их системы.
Логарифмы.
Свойства логарифмов.
Десятичные и натуральные логарифмы.
Логарифмическая функция ее свойства и график.
Логарифмические уравнения и неравенства и их системы.
Дифференцирование показательной и логарифмической функций.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Иметь наглядное представления об основных свойствах показательных и логарифмических функций.
Уметь изображать графики показательных и логарифмических функций.
Описывать свойства показательных и логарифмических функций, опираясь на график.
Уметь решать показательные и логарифмические уравнения.
Уметь решать показательные и логарифмические неравенства.
Уровень возможной подготовки обучающегося
Иметь наглядное представления об основных свойствах показательных и логарифмических функций, уметь иллюстрировать их с помощью графических изображений.
Уметь изображать графики показательных и логарифмических функций. Описывать свойства этих функций, опираясь на график.
Уметь использовать свойства функции для сравнения и оценки ее значений.
Уметь решать показательные и логарифмические уравнения и неравенства, применяя различные методы их решения.
Уровень обязательной подготовки выпускника
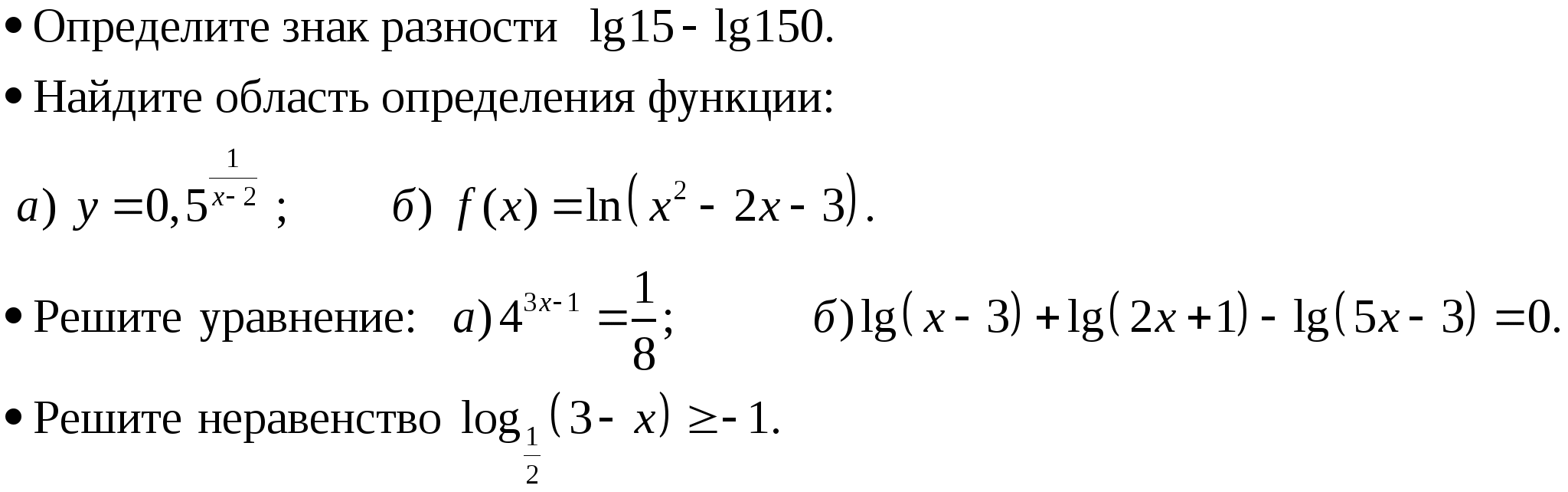
Уровень возможной подготовки выпускника
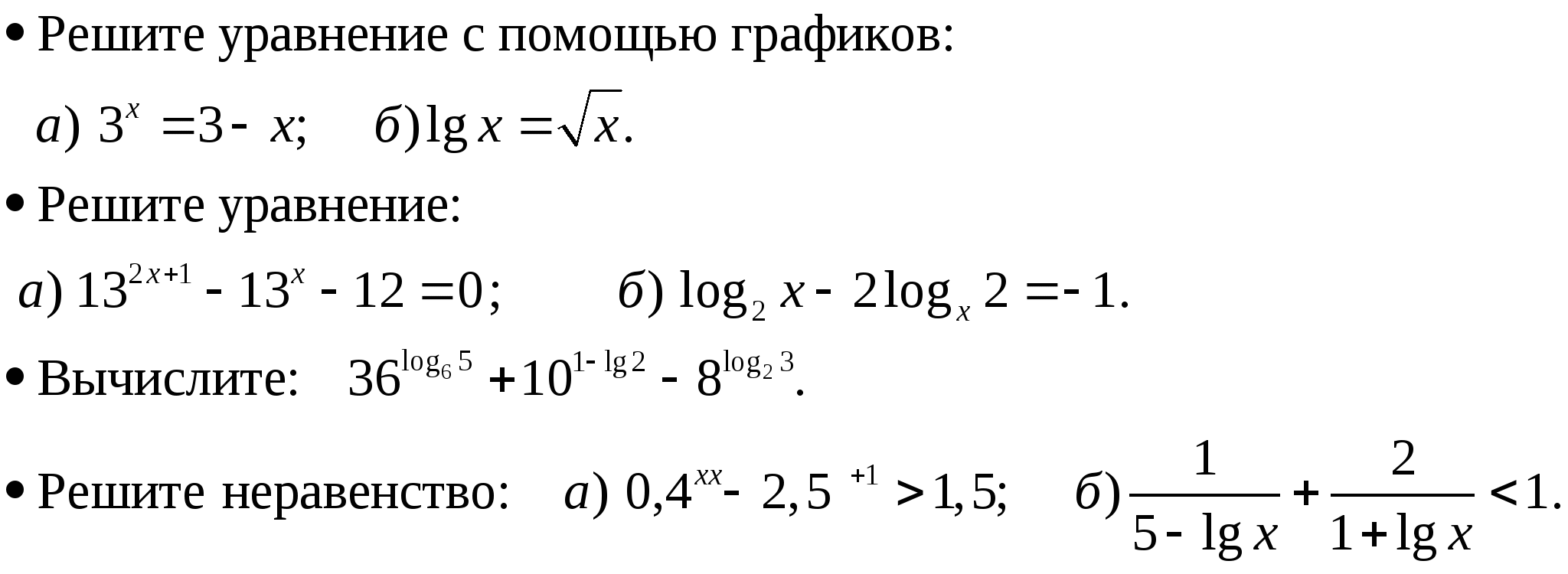
Тема 4. «Первообразная и интеграл» (12 часов)
Раздел математики. Сквозная линия
Функции
Обязательный минимум содержания образовательной области математика
-
Первообразная.
-
Основное свойство первообразной.
-
Правила нахождения первообразных.
-
Площадь криволинейной трапеции.
-
Вычисление интегралов.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь находить первообразные, пользуясь таблицей первообразных.
Знать свойство первообразной.
Знать правила нахождения первообразных.
Уметь вычислять интегралы в простых случаях.
Уметь находить площадь криволинейной трапеции.
Уровень возможной подготовки обучающегося
Освоить технику нахождения первообразных.
Усвоить геометрический смысл интеграла.
Освоить технику вычисления интегралов.
Научиться находить площади фигур в более сложных случаях.
Уровень обязательной подготовки выпускника

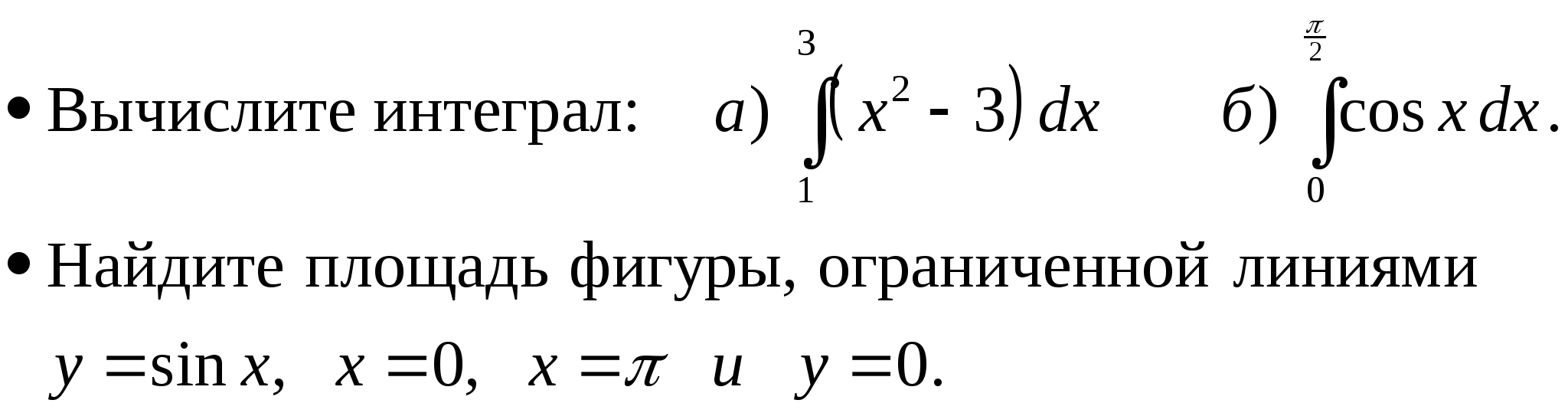
Уровень возможной подготовки выпускника

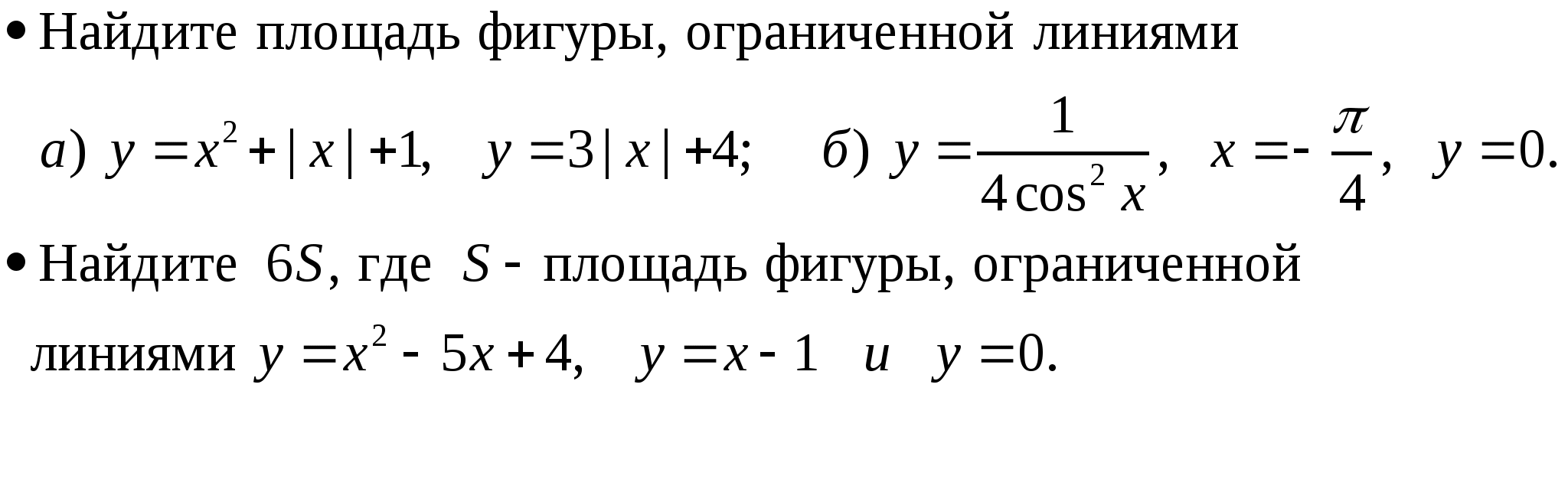
Тема 5 «Элементы математической статистики, комбинаторики и теории вероятностей» (18 часов)
Раздел математики. Сквозная линия
Числа и вычисления.
Множества и комбинаторика.
Статистика.
Вероятность.
Обязательный минимум содержания образовательной области математика
-
Статистическая обработка данных.
-
Сочетания и размещения в комбинаторике.
-
Случайные события и их вероятности.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь решать комбинаторные задачи.
-
Уметь извлекать информацию, представленную в таблицах, на диаграммах, графиках.
-
Уметь составлять таблицы, строить диаграммы, графики.
-
Уметь вычислять средние значения результатов измерений.
-
Уметь находить вероятности случайных событий в простейших случаях.
Уровень возможной подготовки обучающегося
-
Уметь находить частоту события, используя собственные наблюдения и готовые статистические данные.
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения учебных и практических задач, требующих систематического перебора вариантов.
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией.
-
Понимать различные статистические утверждения.
Уровень обязательной подготовки выпускника
-
Сколькими способами могут разместиться 6 человек в салоне автобуса на шести свободных местах?
-
Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 3, 4, 5?
-
Из 12 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать такой выбор?
-
Какова вероятность того, что при бросании игрального кубика выпадет более 4 очков?
-
В таблице показан расход электроэнергии некоторой семьей в течение года:
Месяц
1
2
3
4
5
6
7
8
9
10
11
12
Расход электроэнергии, квтч
85
80
74
62
54
68
58
54
58
64
74
86
Построить столбчатую диаграмму расходов электроэнергии семьи в течение года.
Уровень возможной подготовки выпускника
-
Из 20 вопросов к экзамену Вова 12 вопросов выучил, 5 совсем не смотрел, а в остальных что-то знает, а что-то нет. На экзамене в билете будет три вопроса.
а) Сколько существует вариантов билетов?
б) Сколько из них тех, в которых Вова знает все вопросы?
в) Сколько из них тех, в которых есть вопросы всех трех типов?
г) Сколько из них тех, в которых Вова выучил большинство вопросов?
-
Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что:
а) обе они гласные;
б) среди них есть буква «ь»;
в) среди них нет буквы «а»;
г) одна буква гласная, а другая согласная.
Тема 6. «Уравнения и неравенства. Системы уравнений и неравенств» (24 часа)
Раздел математики.
Уравнения и неравенства
Обязательный минимум содержания образовательной области математика
Уравнения с одной переменной.
Равносильность уравнений.
Общие методы решения уравнений.
Системы уравнений.
Неравенства с одной переменной.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы.
Уметь составлять уравнения и неравенства по условию задачи.
Уровень возможной подготовки обучающегося
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей.
Уметь решать уравнения и неравенства, используя различные методы их решения.
Знать и понимать теоремы о равносильности уравнений, уметь использовать их на практике.
Уровень обязательной подготовки выпускника
● Решите уравнение:
![]()
● Решите неравенство:
![]()
● Решите систему уравнений:
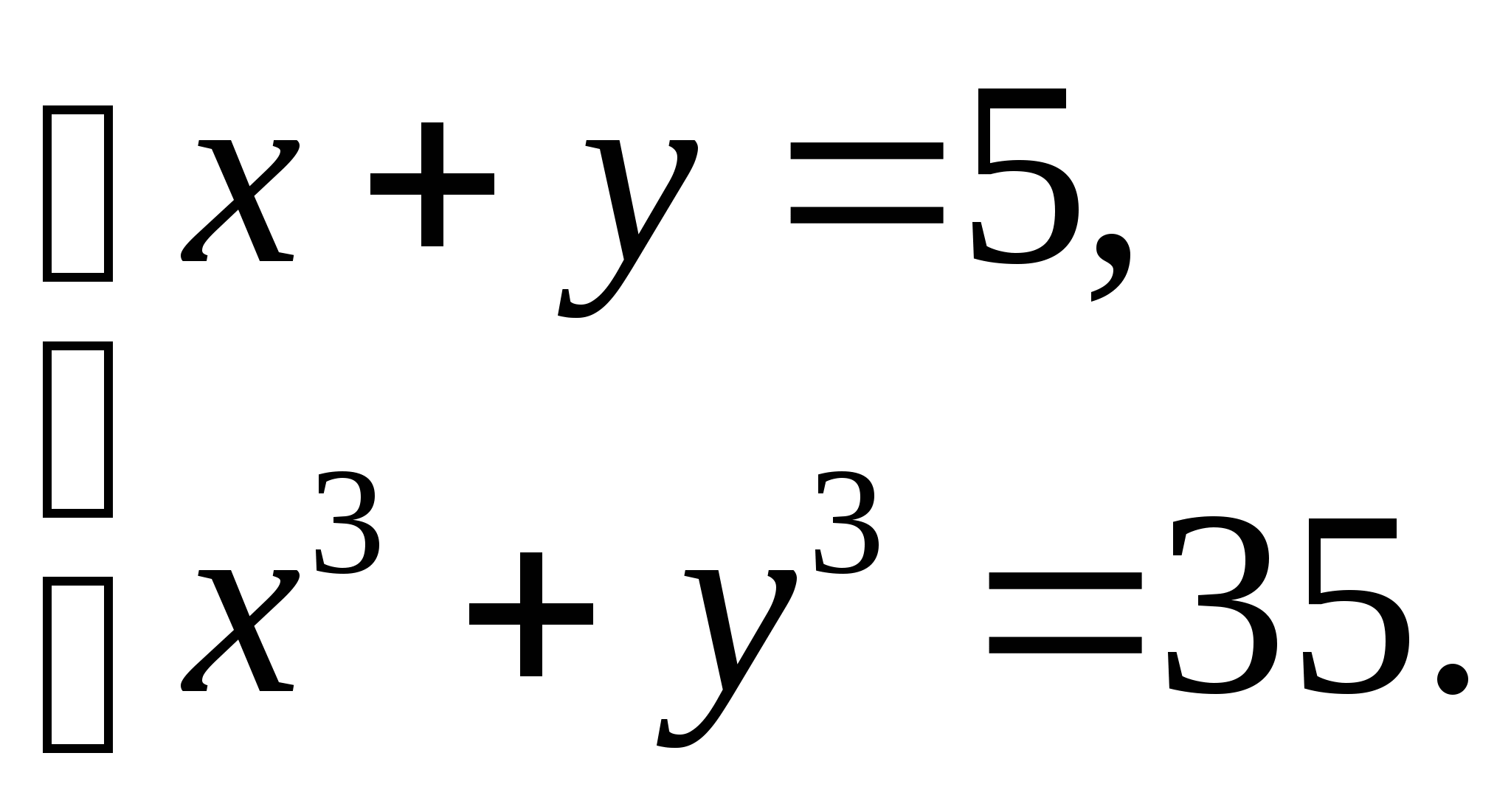
Уровень возможной подготовки выпускника
● Решите уравнение: ![]()
● Решите неравенство: 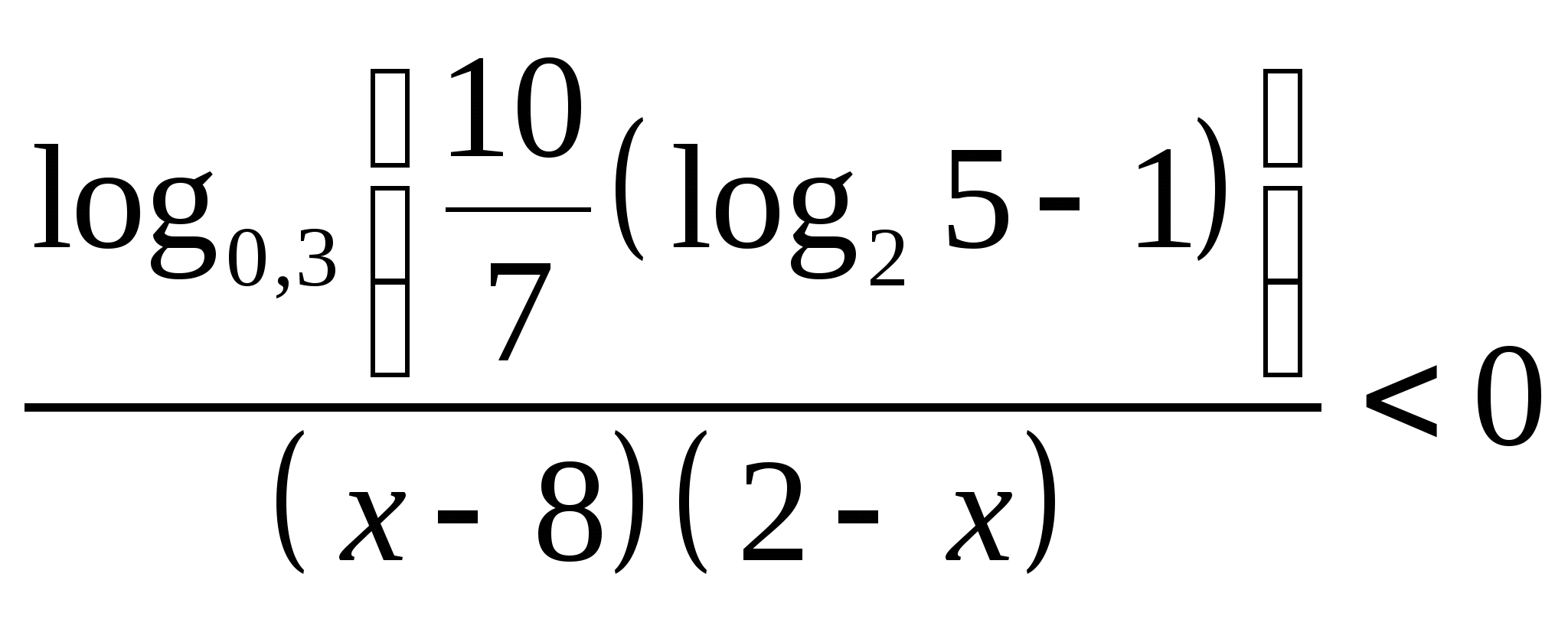
● Решите систему уравнений: 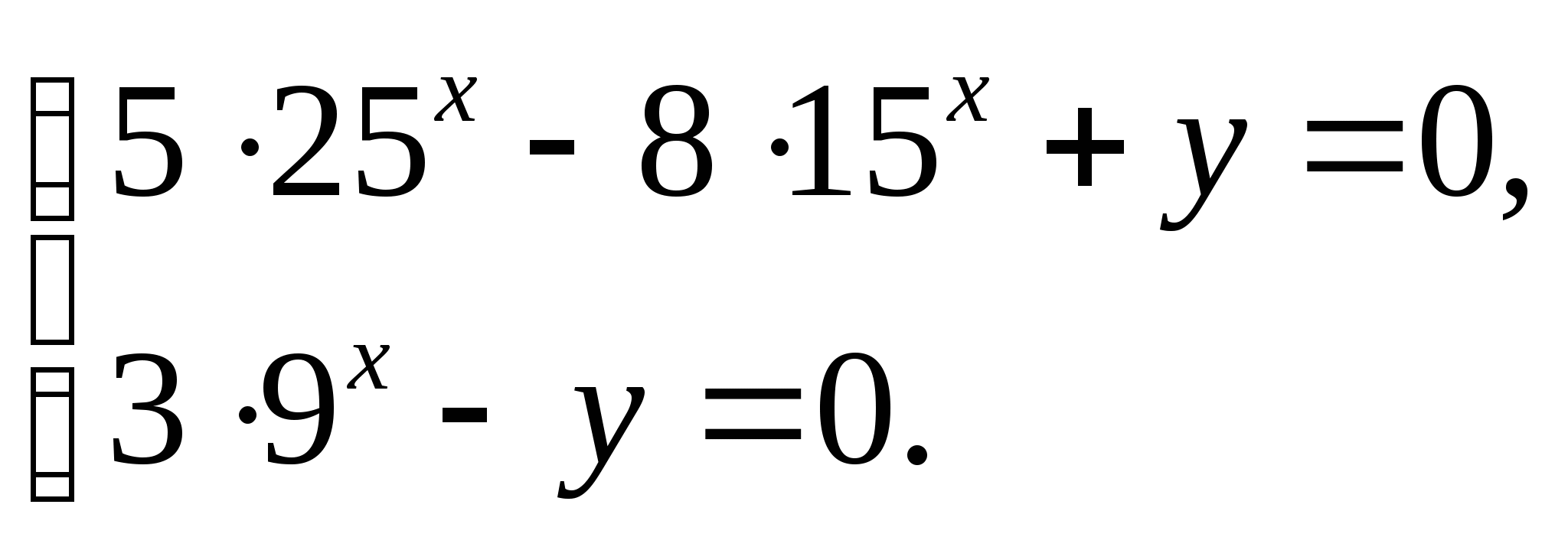
Тема 7. «Итоговое повторение курса
алгебры и начал анализа» (24 часа)
Раздел математики.
-
Вычисления и преобразования
-
Уравнения и неравенства
-
Функции
-
Множества и комбинаторика. Статистика. Вероятность.
Обязательный минимум содержания образовательной области математика
-
Корень степени n.
-
Степень с рациональным показателем.
-
Логарифм.
-
Синус, косинус, тангенс, котангенс. Прогрессии.
-
Общие приемы решения уравнений. Решение уравнений. Системы уравнений с двумя переменными. Неравенства с одной переменной.
-
Область определения функции.
-
Область значений функции.
-
Периодичность. Четность (нечетность). Возрастание (убывание).
-
Экстремумы. Наибольшее (наименьшее) значение.
-
Графики функций.
-
Производная.
-
Исследование функции с помощью производной.
-
Первообразная. Интеграл.
-
Площадь криволинейной трапеции.
-
Статистическая обработка данных.
-
Решение комбинаторных задач.
-
Случайные события и их вероятности.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь:
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций;
-
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
-
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
-
вычислять производные и первообразные элементарных функций, используя справочные материалы;
-
исследовать в простейших случаях функции на монотонность, находить наибольшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
-
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы.
Уровень возможной подготовки обучающегося
-
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
-
вычислять площади с использованием первообразной;
-
использовать для приближенного решения уравнений и неравенств графический метод;
-
изображать на координатной плоскости множества решений простейших уравнений и их систем.
-
строить графики изученных функций;
-
описывать по графику и по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
-
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
-
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
-
построения и исследования простейших математических моделей.
Уровень обязательной подготовки выпускника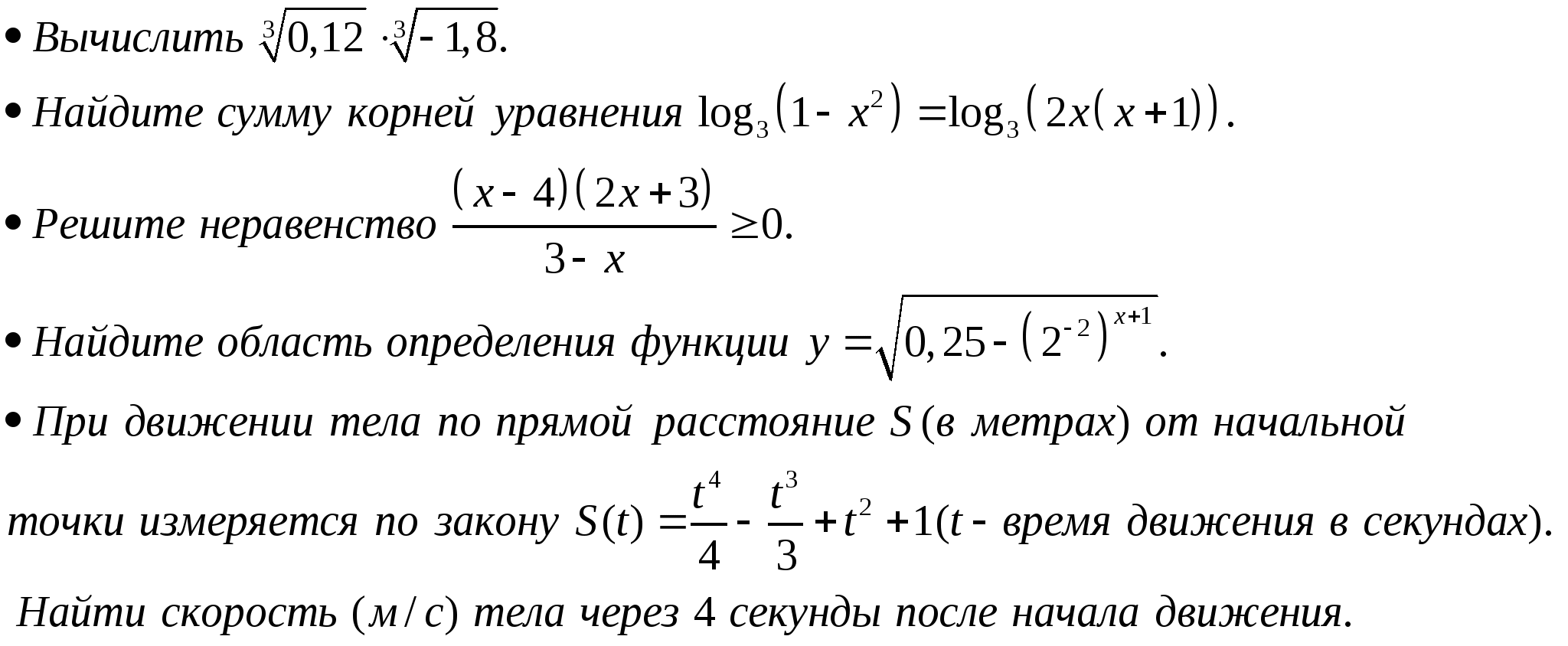
Уровень возможной подготовки выпускника

Литература
-
Бурмистрова Т.А. Алгебра и начала математического анализа. 10 - 11 классы. Программы общеобразовательных учреждений. М., «Просвещение», 2009.
-
Мордкович А.Г. Алгебра и начала математического анализа 10-11 классы. Часть 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень). М.: «Мнемозина», 2009.
-
Мордкович А.Г. и др.Алгебра и начала математического анализа 10-11 классы. Часть 1. Задачник для учащихся общеобразовательных учреждений (базовый уровень). М.: «Мнемозина», 2009.
-
Звавич Л.И. и др. Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы. М.: Дрофа, 1999.
-
Сканави М.И. Сборник задач по математике для поступающих в вузы. Книга 1. Алгебра. М. : ОНИКС 21 век, Мир и образование, 2003.
-
Федеральный компонент государственного стандарта среднего (полного) общего образования по математике //«Вестник образования» -2004 - № 14 - с.107-119.
Интернет-ресурсы
urokimatematiki.ru
intergu.ru/
www.openclass.ru/
festival.1september.ru/articles/subjects/1
www.uchportal.ru/load/23
easyen.ru/
karmanform.ucoz.ru
polyakova.ucoz.ru/
le-savchen.ucoz.ru/</</u>
Электронные учебные пособия
1)Электронный учебник - справочник «Алгебра 7-11 класс»;
2)Математика 5-11 классы. Практикум;
3)Открытая математика.Функции и графики.Версия 2.6.;
4)Уроки алгебры Кирилла и Мефодия. 10-11 кл.;
5)Единый государственный экзамен. Математика.Версия 2.0.
Демонстрационные таблицы
-
Таблицы демонстрационные «Функции и графики».
-
Таблицы демонстрационные «Неравенства. Решение неравенств».
-
Таблицы демонстрационные «Теория вероятностей и математическая статистика».
-
Таблицы демонстрационные «Тригонометрические уравнения, неравенства»
-
Таблицы демонстрационные «Тригонометрические функции»
-
Таблицы демонстрационные «Уравнения. Графическое решение уравнений»
-
Комплект таблиц по алгебре «Алгебра. Формулы. Преобразования выражений»
-
Комплект таблиц по алгебре «Алгебра. Числа. Числовые последовательности»
Календарно- тематическое планирование учебных занятий по алгебре и началам анализа в 11 классе. Ртищевой И.П. 4ч. 132ч в год . РТИЩЕВО
Раздел, название урока
К-во часов
Содержание урока (цель,
основные понятия)
Дата
План
Факт.
Повторение курса алгебры 10 класса- 4 часа
1
Числовые выражения. Преобразования корней
1
формулы сокращенного умножения; правила сокращения дробей, действий с дробями и выражениями, содержащими корни.
доказывать рациональные тождества и упрощать выражения, применяя формулы сокращенного умножения и преобразования корней.
3.09
2
Алгебраические уравнения
1
решения целых алгебраических уравнений, дробно-рациональных уравнений и иррациональных уравнений..
решать целые алгебраические уравнения, дробно-рациональные уравнения и иррациональные уравнений.
5.09
3
Тригонометрические уравнения
1
преобразовывать простые тригонометрические выражения; решать простые тригонометрические уравнения; решать тригонометрические уравнения.
преобразовывать сложные тригонометрические выражения; решать сложные тригонометрические уравнения; вычислять значения выражений, содержащих обратные тригонометрические функциями.
7.09
4
Диагностичес
кая контрольная работа
1
10.09
Глава 6 «Степени и корни. Степенные функции» (20 ч)
5
Понятие корня n-й степени из действительного числа
2
Цель: дать понятие корня n-й степени из действительного числа и корня нечетной степени из отрицательного числа.
-Определение корня n-й степени из действительного числа.
-Определение корня нечетной степени из отрицательного числа.
-Вычислять корень n-й степени из действительного числа.
-Решать уравнения вида xn = a.
11.09
6
Вычисление корня n-й степени из действительного числа
12.09
7
Функции y =![]() ,
,
их свойства и графики
3
Цель: научиться строить и читать графики. Выпуклость вниз и выпуклость вверх.
-Функция
y =![]() , ее свойства
и графики.
, ее свойства
и графики.
-Симметричность графиков
y =![]()
и y = xn
(х > 0) относительно прямой у = х.
-Строить графики, используя основные приемы, и решать с их помощью уравнения и системы уравнений.
14.09
8
Нахождение наибольшего и наименьшего значения функции
17.09
9
Функции y =![]() ,
,
их свойства и графики
18.09
10
Свойства корня n-й степени
3
Цель: научить применять св-ва корня при решении задач
-Теоремы о свойствах корня n-й степени.
-Применять рассмотренные свойства.
19.09
11
Вычисление корней
21.09
12
Возведение в степень
24.09
13
Преобразование выражений, содержащих радикалы
3
Цель: научиться преобразовывать выражения, содержащих радиеалы
-Основные приемы преобразования иррациональных выражений.
-Пользоваться основными приемами для преобразования иррациональных выражений.
25.09
14
Вынесение и внесение множителя под знак корня
26.09
15
Упрощение выражений, содержащих радикалы
28.09
16
Контрольная работа №1 по теме « Степени и корни»
1
Цель: проверить знания и умения по данной теме
1.10
17
Обобщение понятия о показателе степени
3
Цель: понятие степени с дробным показателем.
-Иррациональные уравнения.
-Определение степени с дробным показателем и свойства степени с рациональным показателем.
-Основные приемы решения иррациональных уравнений.
-Выполнять преобразования степени с рациональным показателем.
2.10
18
Вычисление выражений, содержащих степени
3.10
19
Упрощение выражений с показателем степени
5.10
20
Степенные функции, их свойства и
4
Цель: понятие Степенной функции, научиться строить графики и рассмотреть все свойства
-Понятие степенной функции.
-Свойства степенной функции с рациональным показателем.
-Эскизы графиков для любого рационального показателя r.
-Производная степенной функции.
-Строить графики степенных функций.
-Применять изученные свойства для преобразования выражений и решения уравнений.
-Находить производные степенных функций.
12.10
21
Степенные функции и графики
13.10
22
Степенные функции, их свойства и графики
15.10
23
Степенные функции, их свойства и графики
17.10
24
Решение задач
1
Решение тестов
19.10
Глава 7 « Показательная и логарифмическая функции» ( 30 ч)
25
Показательная функция ее свойства и график
3
Цель: Рассмотреть Степень с иррациональным показателем.
-Показательная функция, показательное уравнение, показательное неравенство.
-Понятие показательных функций y=2x и y=(1/2)x, их свойства и графики.
-Определение функции y=ax.
-Теоремы о свойствах показательной функции.
-Графики.
-Строить графики показательной функции.
-Решать простейшие показательные уравнения и неравенства.
-Использовать свойства показательной функции.
20.10
26
Показательная функция ее свойства и график
22.10
27
Показательная функция ее свойства и график
24.10
28
Показательные уравнения.
2
-Понятие показательного уравнения.
-Теорема о показательном уравнении.
-Основные методы решения этих уравнений.
-Решать показательные уравнения, уравнения, сводящиеся к этому виду, и системы показательных уравнений.
26.10
29
Показательные уравнения.
27.10
30
Показательные неравенства
2
-Понятие показательного неравенства.
-Теорема о показательных неравенствах.
-Методы решения этих неравенств.
-Решать показательные неравенства.
29.10
31
Показательные неравенства
31.10
32
Контрольная работа №2 по теме: Показательная функция, уравнения и неравенства»
1
Цель: проверить знания и умения по данной теме.
2.11
33
Понятие логарифма
2
Цель: дать понятие логарифма числа.
-Основание логарифма.
Логарифмирование
-Логарифмические уравнения и неравенства.
-Десятичный логарифм.
-Определение логарифма.
-Формулы, следующие из определения.
-Вычислять логарифмы.
-Решать простейшие уравнения и неравенства.
3.11
34
Понятие логарифма
5.11
35
Логарифмичес
кая функция, ее свойства и график
3
Цель: дать понятие логарифмической функции.
-Понятие логарифмической функции.
-График функции.
-Свойства функции.
-Понятие логарифмической функции.
-График функции.
-Свойства функции.
Применять функционально-графический метод при решении логарифмических уравнений и неравенств.
7.11
36
Логарифмичес
кая функция, ее свойства и график
9.11
37
Логарифмичес
кая функция, ее свойства и график
10.11
38
Свойства логарифмов
3
Цель: вывести и разобрать операции логарифмирования и потенцирования
.
-Основные свойства логарифмов.
-Применять изученные свойства при вычислении логарифмов и решении уравнений.
-Уметь доказывать свойства.
12.11
39
Свойства логарифмов
14.11
40
Свойства логарифмов
23.11
41
Логарифмические уравнения
3
Логарифмическое уравнение
-Понятие логарифмического уравнения.
-Алгоритм решения логарифмических уравнений.
-Три основных метода решения логарифмических уравнений.
-Решать логарифмические уравнения, пользуясь основными приемами и методами.
24.11
42
Логарифмические уравнения
26.11
43
Логарифмические уравнения
28.11
44
Контрольная работа №3 по теме «Решение логарифмических уравнений»
1
Цель: проверить знания и умения по данной теме
30.11
45
Логарифмические неравенства
3
Цель : Ввести и разобрать логарифмическое неравенство
-Понятие логарифмического неравенства.
-Основные приемы и методы решения неравенств этого вида и систем неравенств.
Уметь решать логарифмические неравенства, пользуясь основными приемами и методами.
1.12
46
Логарифмические неравенства
3.12
47
Логарифмические неравенства
5.12
48
Переход к новому основанию логарифма
2
Формула перехода и ее следствия
Применять формулу перехода
7.12
49
Переход к новому основанию логарифма
8.12
50
Дифференцирование показательной и логарифмической функций
3
Цель Ввести понятие числа е и
Натурального логарифма
-Число е.
-Свойства функции y=ex и ее производная.
-Понятие натурального логарифма.
-Свойства функции y=lnx и ее производная.
-Производная показательной и логарифмической функций.
-Уметь вычислять производные рассмотренных функций, применять их в написании уравнения касательной, исследовании изученных функций на монотонность и экстремумы, построения графиков функций, отыскания наибольших и наименьших значений функций на промежутке.
10.12
51
Дифференцирование показательной и логарифмической функций
12.12
52
Дифференцирование показательной и логарифмической функций
14.12
53
Административная контрольная работа №4
по теме : Дифференцирование показательной и логарифмической функции»
1
Цель: проверить знания и умения по данной теме
15.12
54
Решение задач
1
17.12
Глава 8 « Первообразная и интеграл » (12ч)
55
Первообразная
3
Цель: дать определение первообразной
-Понятие первообразной.
-Правила отыскания первообразных.
-Таблица первообразных.
-Уметь находить первообразные известных функций.
19.12
56
Первообразная
21.12
57
Первообразная
22.12
58
Определенный интеграл
6
Цель: дать определение определенного интеграла и
Криволинейной трапеции
-Понятие интеграла.
-Геометрический смысл определенного интеграла.
-Формула Ньютона-Лейбница.
-Свойства определенного интеграла.
-Вычислять определенные интегралы и площади плоских фигур.
24.12
59
Криволинейная трапеция
26.12
60
Формула ньютона-лейбница
28.12
61
Площадь криволинейной трапеции
29.12
62
Решение интеграла
31.12
63
Вычисление интеграла
11.01
64
Контрольная работа №5 по теме « Решение определённого интеграла»
1
Цель: проверить знания и умения по данной теме
12.01
65
Решение задач
2
Анализ контрольной работы. Решение тестовых задач
14.01
66
Решение задач
16.01
Глава 9 «Элементы математической статистики,
комбинаторики и теории вероятностей» (18ч)
67
Статистическая обработка данных.
3
Цель: разобрать теорию по статистике и по вероятности, научиться применять на практике.
-Три графических изображения распределения данных.
-Основные этапы простейшей статистической обработки данных.
-Числовые характеристики измерения (объем, размах, мода и среднее).
-Варианта измерения, ряд данных, сгруппированный ряд данных, медиана измерения.
-Кратность варианты(опрделение).
-Частота варианты (две формулы)..
-Различать и применять рассмотренные понятия на примерах учебника.
.
18.01
68
Статистическая обработка данных.
19.01
69
Статистическая обработка данных.
21.01
70
Простейшие вероятностные задачи.
3
Цель: разобрать теорию по комбинаторике и научиться решать задачи.
-Классическое определение вероятности.
-Алгоритм нахождения вероятности случайного события.
-Правило умножения.
-Уметь находить вероятность случайного события.
-Уметь находить вероятность случайного события.
23.01
71
Простейшие вероятностные задачи.
25.01
72
Простейшие вероятностные задачи.
26.01
73
Сочетания и размещения.
4
Цель дать понятие факториала, размещения, сочетания.
-Факториал.
-Формула числа перестановок.
-Понятие числа сочетаний.
-Теорема о выборе двух элементов без учета их порядка.
-Понятие числа размещений.
-Теоремы о размещениях и сочетаниях.
-Уметь вычислять число сочетаний и размещений по формулам.
-Пользоваться треугольником Паскаля.
28.01
74
Сочетания и размещения.
30.01
75
Сочетания и размещения.
1.02
76
Сочетания и размещения.
2.02
77
Формула бинома Ньютона.
2
Цель: ввести формулу Бинома, биноминальные коэффициенты.
Формула бинома Ньютона.
Пользоваться формулой бинома Ньютона.
4.02
78
Формула бинома Ньютона.
6.02
79
Случайные события и их вероятности.
4
Произведение событий, сумма двух событий, независимость событий, теорема Бернулли и статистическая устойчивость.
Геометрическая вероятность.
Применение комбинаторики в более сложных вероятностных задачах.
Пользоваться введенными понятиями и теоремами для решения задач.
8.02
80
Случайные события и их вероятности.
9.02
81
Случайные события и их вероятности.
11.02
82
Случайные события и их вероятности.
13.02
83
Административная контрольная работа №6 по теме « Формула Бинома-Ньютона, Случайные события»
1
Цель: проверить знания и умения по данной теме
15.02
84
Решение задач
1
Тесты егэ
16.02
Глава 10 Повторение.
Уравнения и неравенства. Системы уравнений и неравенств.(24)
85
Равносиль
ность уравнений.
2
Цель: дать понятие равносильности уравнений.
-Понятие равносильных уравнений.
-Понятие следствия уравнения.
-Теоремы о равносильности уравнений.
-Три этапа в решении уравнений.
-Причины проверки корней.
-Причины потери корней.
-Уметь делать вывод о расширении ОДЗ, о необходимости проверки корней, о вероятности потери корней.
18.02
86
Равносиль ность уравнений.
20.02
87
Общие методы решения уравнений.
3
Общие методы решения уравнений
Общие методы решения уравнений
Уметь пользоваться каждым из 4 методов.
.
29.02
88
Общие методы решения уравнений.
1.03
89
Общие методы решения уравнений.
3.03
90
Решение неравенств с одной переменной.
4
Цель: применять равносильность при решении неравенств с одной переменной, а так же совокупность неравенств и
частные и общие решения.
-Понятия равносильных неравенств и следствия неравенства.
-Теоремы о равносильности неравенств.
Понятия системы и совокупности неравенств, их частными и общими решениями.
-Иррациональные неравенства.
-Уметь решать неравенства и системы с одной переменной.
-В несложных случаях решать иррациональные неравенства и неравенства с модулем.
5.03
91
Решение неравенств с одной переменной.
7.03
92
Решение неравенств с одной переменной.
8.03
93
Решение неравенств с одной переменной.
10.03
94
Уравнения и неравенства с двумя переменными
3
Понятие решения уравнения и неравенства с двумя переменными
Применять графический метод .
-Находить целочисленные решения.
12.03
95
Уравнения и неравенства с двумя переменными
14.03
96
Уравнения и неравенства с двумя переменными
15.03
97
Системы уравнений.
5
Понятие системы уравнений и равносильных систем уравнений.
Пользоваться основными алгоритмическими приемами решения систем уравнений.
17.03
98
Системы уравнений.
19.03
99
Системы уравнений.
21.03
100
Системы уравнений.
22.03
101
Системы уравнений.
24.03
102
Уравнения и неравенства с параметрами.
2
Цель: дать понятие параметра. Научиться решать его в задачах.
Понятие параметра
Дать представление о том, как нужно рассуждать при решении уравнений и неравенств с параметрами.
26.03
103
Уравнения и неравенства с параметрами.
28.03
104- 105
Контрольная работа №7 по теме: Уравнения и неравенства с параметрами»
2
Цель: проверить знания и умения по данной теме
29.03
106
Решение задач
3
Задания из КИМов
Решение задач с параметрами.
31.03
107
Решение задач
2.04
108
Решение задач
Итоговое повторение (24 ч)
109
Функции
4
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Обратная функция. Область определения и область значений обратной функции. График обратной функции. Степенная функция с натуральным показателем, ее свойства и график.Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.Тригонометрические функции, их свойства и графики; периодичность, основной период.Показательная функция (экспонента), ее свойства и график. Логарифмическая функция, ее свойства и график.Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат.
4.04
110
Область определения функции
5.04
111
Область значения функции
7.04
112
Исследование функции
9.04
113
Уравнения
8
Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных уравнений. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
18.04
114
Системы уравнений
19.04
115
Уравнения и системы уравнений
21.04
116
Уравнения и системы уравнений
23.04
117
Уравнения и системы уравнений
25.04
118
Уравнения и системы уравнений
26.04
119
Уравнения и системы уравнений
28.04
120
Уравнения и системы уравнений
30.04
121
Решение неравенств
4
2.05
122
Решение неравенств
3.05
123
Решение неравенств
5.05
124
Решение неравенств
7.05
125
Числа и алгебраические преобразования
3
Корни и степени. Корень степени n > 1 и его свойства. Степень с рациональным показателем и ее свойства. Свойства степени с действительным показателем.
Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень .
10.05
126
Числа и алгебраические преобразования
12.05
127
Числа и алгебраические преобразования
14.05
128
Административная контрольная работа по всему курсу алгебры.
1
Цель: проверить знания и умения в виде тестов.
В тестовой форме.
16.05
129
Решение задач ЕГЭ
4
Задачи по темам «Натуральные и рациональные числа»
17.05
130
Решение задач
19.05
131
Решение задач
21.05
132
Решение задач
23.05