- Учителю
- Разработка урока геометрии на тему: 'Площадь фигур' (8 класс)
Разработка урока геометрии на тему: 'Площадь фигур' (8 класс)

 Тема «Площадь фигур»
Тема «Площадь фигур»
Методическая цель: использование стратегий развития критического мышления, проблемно-развивающей технологии обучения и ИКТ с целью реализации компетентностного подхода.
Тип урока:
Урок применения и совершенствования знаний.
Учебные цели.
1. Повторить теоретический материал: определения, признаки, свойства, формулы для вычисления площадей треугольника, параллелограмма, квадрата, прямоугольника, ромба, трапеции.
2. Рассмотреть задачи прикладного характера на вычисление площадей фигур.
3.Воспитывать умение организовывать себя в процессе интеллектуальной деятельности
Прогнозируемый результат:
-
Знать основные свойства фигур, формулы площадей параллелограмма, треугольника, трапеции.
-
Уметь применять свойства фигур, формулы площадей фигур при решении задач практического содержания.
Оборудование:
-
Чертежные инструменты.
-
Интерактивная доска.
-
Раздаточный материал.
ХОД УРОКА
-
Организационный момент
-
Проверка домашнего задания
-
Целеполагание
Заполнение таблицы ЗХУ.
-
Актуализация знаний
-
Деление на группы (по конфетам 5 видов)
-
Составления постера «Геометрическая фигура»: треугольник, параллелограмм, квадрат, прямоугольник, ромб, трапеция (каждая группа должна отразить на постере определение, признаки, свойства, формулы).
-
Стратегия «Вернисаж». Взаимооценка (формативное оценивание) работы одноклассников.
-
Математическая разминка «Кроссворд»
| Кроссворд «Четырёхугольники»
|
|
|
|
|
|
|
|
| 5 |
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8 |
|
| 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По горизонтали:
-
Четырехугольник, у которого противоположные стороны параллельны.
-
Четырехугольник, у которого только две противоположные стороны параллельны.
-
Параллелограмм, у которого все углы прямые.
-
Точка, из которой выходят две стороны четырехугольника.
По вертикали:
-
Сумма длин всех сторон.
-
Отрезок, соединяющий противоположные вершины четырехугольника.
-
Прямоугольник, у которого все стороны равны.
-
Параллелограмм, у которого все стороны равны.
-
Отрезок, соединяющий соседние вершины.
-
Одна из параллельных сторон трапеции.
-
Практическая работа
Работает класс индивидуально 5 минут (у каждого условие задачи).
После учитель проверяет правильность и разрабатывает вместе с детьми алгоритм решения (форма - беседа).
Задача 1
Оштукатуренная стена длиной 8,25 м и высотой 4,32 м имеет три окна размером 2,2м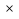 1,2м каждое. Найти площадь стены, покрытой штукатуркой.
1,2м каждое. Найти площадь стены, покрытой штукатуркой.
Решение
1.Найдем площадь стены S = 8,25 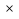 4,32= 35,64 кв.м.
4,32= 35,64 кв.м.
2.Найдём площадь окна S = 2,2 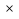 1,2 =2,64 кв. м.
1,2 =2,64 кв. м.
3.Найдём площадь трёх окон S = 2,64 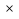 3=7,92 кв.м.
3=7,92 кв.м.
4.Найдём площадь оштукатуренной части стены
S = 35, 64 -7, 92=27, 72 кв. м
Ответ: 27,72 кв. м
Работа в парах. Взаимопроверка «пара на пару». Правильное решение на доске.
Задача 2
Директор разделил стадион на 2 катка. Один квадратной, а второй прямоугольной формы, причем по площади эти катки равны. Площадь всего стадиона 800 м кв. Одна из сторон второго катка равна 40 м. На Новый год для украшения были куплены 2 гирлянды разной длины украшение по периметру). Какой из катков нужно украсить гирляндой наименьшей длины? Чему равна длина гирлянды?
-
Поведение итогов
Заполнение таблицы ЗХУ
Информация о домашнем задании Задача №3
Задача 3
Фронтон имеет форму равнобедренного треугольника АВС. Его ширина АВ равна 9,6м, длина по скату АС равна 6 метрам. Определить сколько досок необходимо для закрытия ими фронтона, если на каждый квадратный метр требуется 2,5 доски.
Решение.
С
6м 6м 6м
А К 9,6м В
1.∆АСВ - равнобедренный. Проведём высоту, она в равнобедренном треугольнике будет медианой. Поэтому разделит основание на две равные части (9,6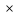 2=4,8).
2=4,8).
Треугольник АКС прямоугольный, по теореме Пифагора найдём высоту СК. СК=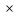 =
=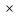 =3,6 м.
=3,6 м.
2.Теперь найдём площадь фронтона. S=(9,6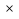 3.6)
3.6)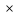 2=17,28кв.м.
2=17,28кв.м.
3.Если на 1кв.м. требуется 2,5 доски, то для закрытия фронтона необходимо 17,28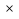 2,5=43,2 доски т.е.44 доски.
2,5=43,2 доски т.е.44 доски.
Ответ:44 доски.
Рефлексия (стратегия «Лестница успеха»)