Зачет по главе Многоугольники

Зачет по главе «Четырехугольники»

Вариант 1

Определите, верны ли утверждения:

1. Сумма противолежащих углов параллелограмма равна 180°.

2. Параллелограмм, диагонали которого взаимно перпендикулярны, является ромбом.

Выбор утверждений:

Укажите номера неверных утверждений:

1. В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

2. Если один из острых углов прямоугольного треугольника равен 18°, то и другой равен 18°.

3. Если диагонали параллелограмма перпендикулярны, то он является ромбом.

Вычисляем:

1. Найдите большую сторону параллелограмма, если его периметр равен 26 и одна сторона на 5 больше другой.

2. Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Найдите длины этих отрезков.

Моделируем:

1. Радиомачта закреплена на растяжках, идущих от середины мачты до точек крепления к земле. Найдите длину растяжек (в метрах), если они расположены под углом 60° к мачте, а ее высота равна 24 метра.

2. Сколько осей симметрии имеет буква Н, изображенная на рисунке?

3. Какой из дорожных знаков, изображенных на рисунке, имеет только одну ось симметрии?

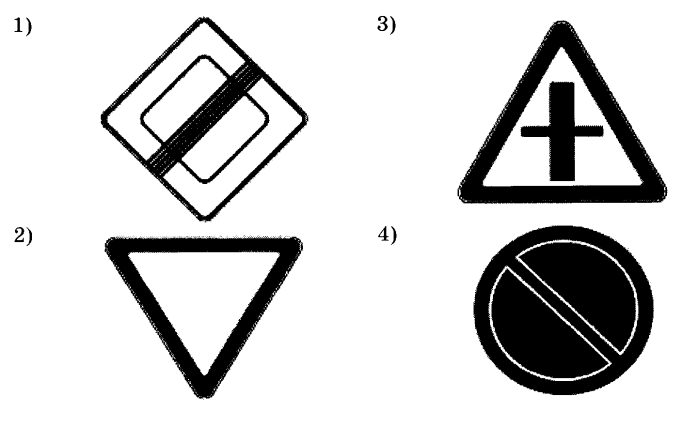
Доказываем:

Докажите, что угол между высотами параллелограмма, проведенными из вершины острого угла, равен большему углу параллелограмма.

Зачет по главе «Четырехугольники»

Вариант 2

Определите, верны ли утверждения:

1. Сумма противолежащих углов равнобедренной трапеции равна 180°.

2. Параллелограмм, диагонали которого равны, является прямоугольником.

Выбор утверждений:

Укажите номера неверных утверждений:

1. В равнобедренном треугольнике медиана является биссектрисой.

2. Если диагонали параллелограмма равны, то он является квадратом.

3. Сумма острых углов прямоугольного треугольника равна 90°.

Вычисляем:

1. Периметр параллелограмма равен 49, одна из его сторон в 6 раз больше другой. Найдите меньшую сторону параллелограмма.

2. Диагональ прямоугольника равна 28, угол между ними равен 60°. Найдите меньшую сторону прямоугольника.

Моделируем:

1. Радиомачта закреплена на растяжках, идущих от середины мачты до точек крепления к земле. Найдите длину растяжек (в метрах), если они расположены под углом 30° к земле, а ее высота равна 26 метров.

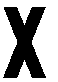
2. Сколько осей симметрии имеет буква Х, изображенная на рисунке?

3. Какой из дорожных знаков, изображенных на рисунке, имеет центр симметрии?

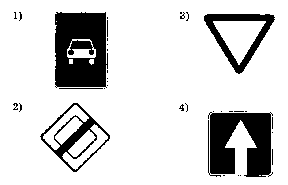
Доказываем:

Точки М и Т делят диагональ АС параллелограмма АВСD на три равных отрезка. Докажите, что четырехугольник ВМDТ - параллелограмм.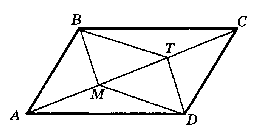

Зачет по главе «Четырехугольники»

Вариант 3

Определите, верны ли утверждения:

1. Сумма углов трапеции, прилежащих к одной стороне, равна 180°.

2. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Выбор утверждений:

Укажите номера верных утверждений:

1. В равнобедренном треугольнике два угла равны.

2. Если диагонали параллелограмма равны, то он является ромбом.

3. Сумма острых углов прямоугольного треугольника равна 180°.

Вычисляем:

1. На продолжении стороны AD параллелограмма ABCD за точку D отмечена точка К так, что DC=DK. Найдите больший угол параллелограмма ABCD, если DKC=48°

2. Диагональ ромба, лежащая против угла в 60°, равна 10. Найдите периметр ромба.

Моделируем:

1. Неогороженный земельный участок имеет форму прямоугольника со сторонами 30 метров и 45 метров. Найдите длину забора, который будет установлен по границе этого участка. Ответ запишите в метрах.

2. Сколько осей симметрии имеет буква п, изображенная на рисунке?

3. Какой из дорожных знаков, изображенных на рисунке, имеет только две оси симметрии?

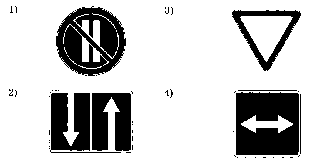
Доказываем:

Докажите, что диагональ параллелограмма разбивает его на два равных треугольника.

Зачет по главе «Четырехугольники»

Вариант 4

Определите, верны ли утверждения:

1. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

2. Четырехугольник, диагонали которого взаимно перпендикулярны, является ромбом.

Выбор утверждений:

Укажите номера неверных утверждений:

1. Диагонали ромба равны.

2. Сумма углов трапеции равна 360°.

3. Если один из смежных углов равен 40°, то и другой угол равен 40°.

Вычисляем:

1. Найдите величину острого угла С параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 38°.

2. Найдите угол АВС равнобедренной трапеции АВСD, если диагональ АС образует с основанием АD и боковой стороной СD углы, равные 30° и 80° соответственно.

Моделируем:

1. Рабочие использовали 122 метра ленты для ограждения котлована прямоугольной формы. Ширина котлована 17 метров. Найдите его длину в метрах.

2. Сколько осей симметрии имеет изображенный на рисунке дорожный знак?

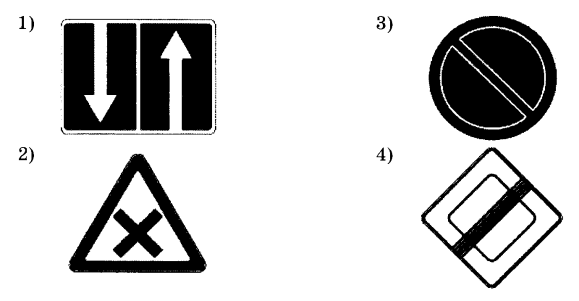
3. Какой из дорожных знаков, изображенных на рисунке, имеет центр симметрии?

Доказываем:

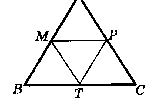
Точки М, Р и Т середины правильного треугольника АВС. Докажите, что четырехугольник АМТР - ромб.

А

Зачет по главе «Четырехугольники»

Вариант 5

Определите, верны ли утверждения:

1. Четырехугольник, две стороны которого параллельны, является параллелограммом.

2. Диагонали равнобедренной трапеции пересекаются и точкой пересечения делятся пополам.

Выбор утверждений:

Укажите номера неверных утверждений:

1. Если при пересечении двух прямых третьей прямой накрест лежащие углы равны 117°, то эти прямые параллельны.

2. Каждая сторона треугольника меньше суммы двух других сторон.

3. Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то эти треугольники равны.

4. Тупоугольным называется треугольник, у которого все углы тупые.

Вычисляем:

1. Диагональ АС параллелограмма АВСDобразует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.

2. Величины углов выпуклого четырехугольника относятся как 1 : 4 : 3 : 2. Найдите больший угол четырехугольника. Ответ дайте в градусах.

Моделируем:

1. Футбольное поле в форме прямоугольника имеет площадь 7140 м². Его длина равна 105 метров. Найдите ширину поля в метрах.

2. Сколько осей симметрии имеет изображенный на рисунке дорожный знак?

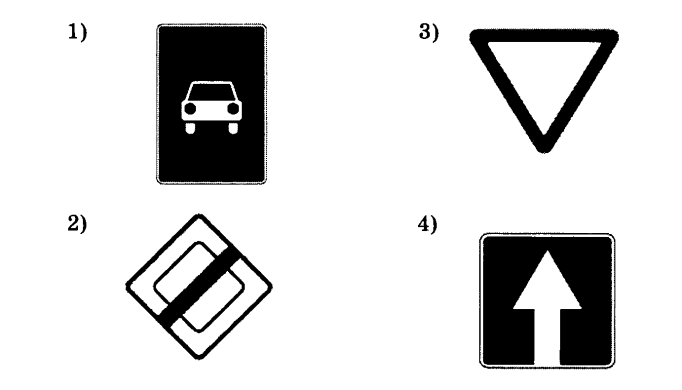
3. Какой из дорожных знаков, изображенных на рисунке, имеет центр симметрии?

Доказываем:

В параллелограмме MKPF проведены высоты КО и КЕ к сторонам МF и РF соответственно, КО=КЕ. Докажите, что МКРF - ромб.

Зачет по главе «Четырехугольники»

Вариант 6

Определите, верны ли утверждения:

1. Четырехугольник, две стороны которого параллельны является параллелограммом или трапецией.

2. Параллелограмм, диагонали которого равны, является ромбом.

Выбор утверждений:

Укажите номера верных утверждений:

1. Сумма углов выпуклого пятиугольника равна 800°.

2. Диагонали прямоугольника лежат на биссектрисах его углов.

3. Две различные прямые, перпендикулярные третьей, параллельны.

4. Треугольник со сторонами 1, 13, 14 не существует.

Вычисляем:

1. Величины углов выпуклого четырехугольника относятся как 3 : 2 : 3 : 4. Найдите меньший угол четырехугольника. Ответ дайте в градусах.

2. Биссектриса угла А параллелограмма АВСD пересекает сторону ВС в точке К так, что ВК : КС= 4 : 3. Найдите большую сторону параллелограмма, если его периметр равен 132.

Моделируем:

1. Радиомачта закреплена на растяжках, идущих от середины мачты до точек крепления к земле. Найдите длину растяжек (в метрах), если они расположены под углом 60° к мачте, а ее высота равна 24 метра.

2. Сколько осей симметрии имеет изображенный на рисунке дорожный знак?

3. Какой из дорожных знаков, изображенных на рисунке, имеет центр симметрии?

Доказываем:

Точки М середина стороны АВ параллелограмма АВСD, СМ=МD. Докажите, что данный параллелограмм - прямоугольник.

Зачет по главе «Четырехугольники»

Вариант 7

Определите, верны ли утверждения:

1. Четырехугольник, две стороны которого параллельны и две стороны равны, является параллелограммом.

2. Диагонали прямоугольника равны.

Выбор утверждений:

Укажите номера неверных утверждений:

1. Если один из углов при боковой стороне трапеции равен 102°, то другой угол равен 78°.

2. Если два угла четырехугольника равны 120°, а два других 60°, то он является параллелограммом.

3. Диагонали ромба равны.

Вычисляем:

1. На продолжении стороны AD параллелограмма ABCD за точку D отмечена точка К так, что DC=DK. Найдите больший угол параллелограмма ABCD, если DKC=48°.

2. Диагональ прямоугольника равна 28, угол между ними равен 60°. Найдите меньшую сторону прямоугольника.

Моделируем:

1. Радиомачта закреплена на растяжках, идущих от середины мачты до точек крепления к земле. Найдите длину растяжек (в метрах), если они расположены под углом 30° к земле, а ее высота равна 26 метров.

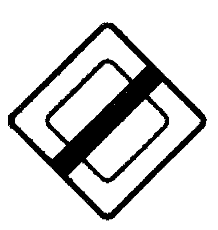
2. Сколько осей симметрии имеет изображенный на рисунке дорожный знак?

3. Какой из дорожных знаков, изображенных на рисунке, имеет только две оси симметрии?

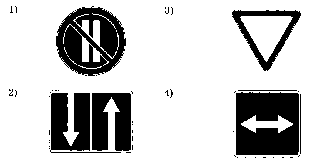
Доказываем:

В параллелограмме АВСD точка Р - середина стороны АD, РВ=РС. Докажите, что АВСD - прямоугольник.

Зачет по главе «Четырехугольники»

Вариант 8

Определите, верны ли утверждения:

1. Противоположные стороны трапеции попарно параллельны.

2. Диагонали равнобедренной трапеции равны.

Выбор утверждений:

Укажите номера верных утверждений:

1. Если диагонали параллелограмма перпендикулярны, то он является ромбом.

2. Сумма углов трапеции равна 360°.

3. Сумма двух соседних углов параллелограмма равна 180°.

</

Вычисляем:

1. Найдите периметр параллелограмма АВСD, если ВС=8, угол В равен 30°, а высота проведенная из вершины А, равна 7.

2. Найдите угол АВС равнобедренной трапеции АВСD, если диагональ АС образует с основанием АD и боковой стороной СD углы, равные 30° и 80° соответственно.

Моделируем:

1. Неогороженный земельный участок имеет форму прямоугольника со сторонами 30 метров и 45 метров. Найдите длину забора, который будет установлен по границе этого участка. Ответ запишите в метрах.

2. Сколько осей симметрии имеет изображенный на рисунке дорожный знак?

3. Какой из дорожных знаков, изображенных на рисунке, имеет только одну ось симметрии?

Доказываем:

Точка М - середина АВ ромба АВСD, СМ=МD. Докажите, что данный ромб - квадрат.

Зачет по главе «Четырехугольники»

Вариант 9

Определите, верны ли утверждения:

1. Сумма углов выпуклого четырехугольника равна 180°.

2. Противоположные стороны параллелограмма попарно равны.

Выбор утверждений:

Укажите номера неверных утверждений:

1. Диагонали прямоугольника лежат на биссектрисах его углов.

2. Тупоугольным называется треугольник, у которого все углы тупые.

3. Если один из углов трапеции равен 90°, то и остальные равны 90°.

Вычисляем:

1. Периметр ромба равен 64, один из его углов 120°. Найдите меньшую диагональ ромба.

2. Найдите величину острого угла С параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 38°.

Моделируем:

1. Рабочие использовали 122 метра ленты для ограждения котлована прямоугольной формы. Ширина котлована 17 метров. Найдите его длину в метрах.

2. Сколько осей симметрии имеет изображенный на рисунке дорожный знак?

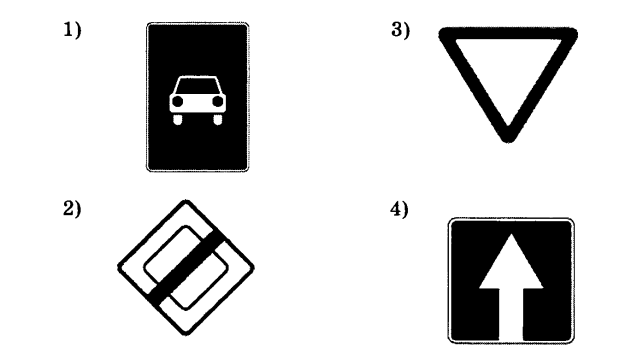
3. Какой из дорожных знаков, изображенных на рисунке, имеет центр симметрии?

Доказываем:

Докажите, что при пересечении биссектрис углов, прилежащих к боковой стороне трапеции, образуются прямые углы.