- Учителю
- Конспект по математике на тему 'Первообразная и интеграл' (10-11 классы)
Конспект по математике на тему 'Первообразная и интеграл' (10-11 классы)
Методическая разработка урока алгебры по теме: «Первообразная и интеграл»
Алгебра и начала анализа, 11 класс. Тема: Интеграл
Автор: Жилякова Любовь Николаевна, преподаватель математики ГБОУ СПО «Слободотуринский аграрно-экономический техникум»
Описание материала: предлагаю вам конспект урока для учащихся по теме: «Первообразная и Интеграл». Данный материал будет полезен педагогам, при обобщении и систематизации знаний, полученных при изучении данного раздела и поможет расширить представления учащихся о практическом значении данной темы.
Тема: «Первообразная и интеграл»
Тип: урок обобщения и систематизации знаний.
Форма: игра
Цели:
дидактические:
-
формирование учебно-познавательной и информационной компетенций, посредством обобщения, систематизации знаний по теме «Первообразная. Интеграл», формирования навыков нахождения площади криволинейной трапеции несколькими способами.
развивающие:
-
формирование информационной, общекультурной компетенций через развитие познавательной активности, интереса к предмету, творческих способностей учащихся, расширение кругозора, развитие математической речи.
воспитательные:
-
формирование коммуникативной компетенции и компетенции личностного самосовершенствования, посредством работы над коммуникативными навыками, умением работать в сотрудничестве, над воспитанием таких личностных качеств, как организованность, дисциплинированность.
Средства обучения:
Технические: ПК, проектор, экран.
Ход урока
Подготовительный этап: группа заранее делится на две команды.
I. Организационный момент
Здравствуйте, ребята! Я рада приветствовать вас на уроке. Цель нашего урока - обобщить, систематизировать знания по теме « Первообразная и интеграл», подготовиться к предстоящему зачету.
Девиз нашей работы: «Исследуй всё, пусть для тебя на первом месте будет разум» - эти слова принадлежат древнегреческому ученому Пифагору. (слайд )
Мы совершим необычное восхождение на вершину «Пика знаний».
Первенство будут оспаривать две группы. У каждой группы свой инструктор, который оценивает коэффициент участия каждого «туриста» в нашем восхождении.
Группа, которая первой достигнет вершины «Пика знаний», станет победителем.
II. Проверка домашнего задания: «Проверим рюкзаки»
Перед дальней дорогой нужно проверить насколько хорошо вы подготовились к восхождению. Проверим домашнее задание, которое было задано на предыдущем уроке:
Найти площадь фигуры ограниченной линиями:
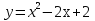 ,
, 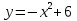
два человека по очереди выходят к доске кратко объясняют решение, которое
они заранее заготовили на слайдах. Остальные в это время проверяют.
III. Разминка.
Принято, что человек, готовясь к соревнованию, свой день обычно начинает с зарядки, то есть с разминки.
Проведем разминку и мы.
Предлагается 9 тестовых заданий. Каждая команда по очереди выбирает вопрос, за правильные ответы получают жетоны (слайд)
-
Множество всех первообразных функции
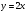 имеет вид …
имеет вид …
-
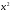 ;
; -
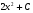 ;
; -
2;
-
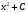 ;
; -
2+
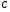 .
.
-
Операция нахождения неопределённого интеграла от некоторой функции называется…
-
интегрированием;
-
дифференцированием;
-
логарифмированием;
-
возведением в степень;
-
извлечением корня.
-
Множество всех первообразных функции
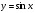 имеет вид …
имеет вид …
-
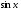 ;
; -
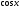 ;
; -
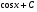 ;
; -
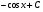 ;
; -
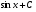 .
.
-
Закончите определение:
Неопределённым интегралом от функции y = f(x) называется:
-
производная функции F(x);
-
совокупность всех первообразных функции y = f(x);
-
совокупность всех производных функции y = f(x);
-
знак вида .
-
Множество всех первообразных функции
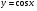 имеет вид …
имеет вид …
-
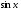 ;
; -
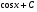 ;
; -
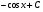 ;
; -
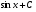 .
.
-
Выберите правильный вариант ответа:
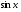 …
…
-
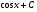 ;
; -
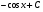 ;
; -
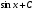 ;
; -
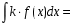 .
.
-
Формула Ньютона-Лейбница:
-
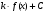 ;
; -
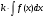 ;
; -
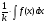 ;
; -
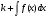 .
.
-
Выберите правильный вариант ответа:
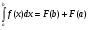
-
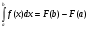 ;
; -
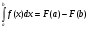 ;
; -
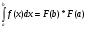 ;
; -
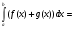 .
.
IV. Математическая эстафета.
Теперь в путь! Подъем к «Пику знаний» будет нелегким, могут быть и завалы, и обвалы, и заносы. Но есть и привалы, где вас ждут не только задания. Чтобы продвинуться вперед, надо показать знания.
Работа в командах. На последней парте каждого ряда находится листок с 8 заданиями (по два вопроса на каждую парту). Первая пара учащихся, выполнив любые два задания, передает листок впереди сидящим. Работа считается оконченной, когда учитель получается листок с правильно выполненными 8 заданиями. Те же задания представлены на слайде. Вы можете решить не только свои задания, что проверить правильность решения членов своей команды.
Побеждает та команда, которая раньше всех решит все задания. Проверка работ осуществляется с помощью слайда. Заработанные баллы суммируются.
-
Найдите неопределенный интеграл и сделайте проверку:
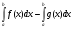 .
. -
Вычислите определенный интеграл:
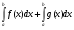 .
. -
Найдите неопределенный интеграл и сделайте проверку:
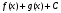 .
. -
Вычислите определенный интеграл:
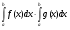 .
. -
Вычислите определенный интеграл:
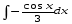 .
. -
Вычислите определенный интеграл:
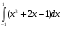 .
. -
Вычислите определенный интеграл:
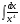 .
. -
Найдите неопределенный интеграл и сделайте проверку:
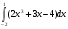 .
.
А теперь привал.
V. Привал.
«Счастливая случайность выпадает лишь на долю подготовленных умов» (Луи Пастер) (слайд)
Зачитываются сведения из истории интегрального исчисления (слайд).
(Сведения из истории интегрального исчисления заранее готовятся учащимися и для выступления выбирается лучшее)
VI. Самое трудное восхождение.
Следующее задание предполагается выполнять в письменной форме, поэтому учащиеся работают в тетрадях.
Задача. Сколькими способами можно найти площадь фигуры, ограниченной линиями (слайд)
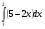 ,
, 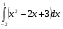 ,
, 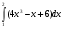 ,
, 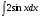
У кого есть предложения? (фигура состоит из двух криволинейных трапеций и прямоугольника) (выбирайте способ решения слайд)
После обсуждения данной проблемы на слайде появляется запись:
1 способ: S=S1+S2+S3
2 способ: S=S1+SABCD-SOCD
Двое учащихся решают у доски с последующим объяснением решения, остальные учащиеся работают в тетрадях, выбрав один из способов решения (по одному человеку от команды)
Вывод (делают учащиеся): мы нашли два способа решения данной задачи, получив один и тот же результат. Обсудить какой способ проще.
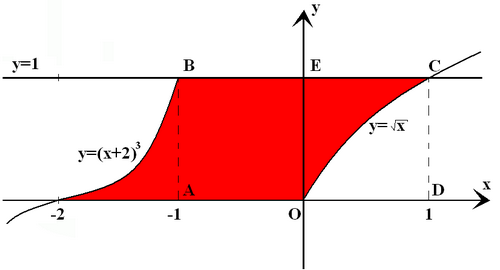
VII. Последний подъем. Кроссворд (слайд)
-
Графиком функции у=kх+b является…
-
Самая низкая школьная оценка.
-
Какой урок контроля знаний проходит обычно перед зачетом?
-
Синоним слова «дюжина».
-
Есть в каждом слове, у растения и может быть у уравнения.
-
Что можно вычислить при помощи интеграла?
-
Одно из важнейших математических понятий.
-
Форма урока, на котором проводится проверка знаний.
-
Немецкий ученый, в честь которого названа формула, связывающая площадь криволинейной трапеции и интеграл.
-
конь - лошадь - жеребенок, бык-корова-теленок, король-королева-принц, граф-графиня - …?
-
Зависимость между множествами х и у, при которой каждому значению из множества х соответствует единственное значение из множества у называется …
Все очень устали, но чем ближе к цели, тем задания становятся все легче и легче.
Последний подъем. На слайде кроссворд. Ваша задача - решить его. По очереди каждая команда отгадывает понравившееся слово, записывает ответ.
VШ. Итог урока (слайд)
Команды подсчитывают количество, заработанных жетонов.
«Мышление начинается с удивления», - заметил 2 500 лет назад Аристотель. Наш соотечественник Сухомлинский считал, что «чувство удивления - могучий источник желания знать; от удивления к знаниям - один шаг». А математика замечательный предмет для удивления.
А знаете ли вы?
Что интегралы используются при:
-
решении задач из области физики;
-
решении экономических задач (на оптимизацию работы фирмы в условиях конкуренции, расчет о доходности потребительского кредита);
-
решении социально - демографических задач (математическая модель народонаселения Земли и др.).
IX. Домашнее задание на выбор(слайд)
-
Придумать еще один способ нахождения площади фигуры, рассмотренной на уроке.
2. Составить и решить 2 задания по типу:
а) Вычислить F(x) для f(x),
б) вычислить интеграл.
X. Выставление отметок.
Домашнее задание
S = S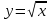 - S
- S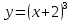 =
= 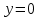 dx -
dx - 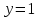 dx =
dx = 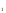 =
=
= dx S=
dx S= dx =
dx =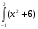 dx = (-
dx = (-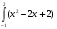 |
|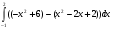 =-
=- 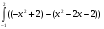 (кв. ед.)
(кв. ед.)
y
O
6
2
-2
2
x
y=x2-2x+2
y=-x2+6
-1
1
Задача.
Сколькими способами можно найти площадь фигуры, ограниченной линиями
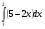 ,
, 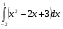 ,
, 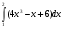 ,
, 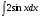
Кроссворд
8