- Учителю
- конспект урока алгебры для 8 класса
конспект урока алгебры для 8 класса
Сценарий урока алгебры в 8 классе по теме «Определение квадратного уравнения. Неполные квадратные уравнения».
Преподавание ведется по программе : «Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала анализа. 10-11 классы»/ авт.-сост. И.И. Зубарева, А.Г. Мордкович. - М.: Мнемозина, 2010. - 64с. (102 часа в год, 3 часа в неделю)
Учебник: «Алгебра. 8 класс»/ А.Г. Мордкович и др. - М.: Мнемозина, 2010.Данный урок относится к разделу «Квадратные уравнения», всего на тему программой отводится 21 урок, данный урок является первым в данной теме.
Это урок изучения нового материала, на котором учитель отдает предпочтение самостоятельной работе обучающихся на всех этапах урока, так как в своей работе использует технологию индивидуального обучения Ю.А. Макарова, курсовую подготовку по которой прошла в 1998 году. Одним из основных принципов в этой технологии является первоначальное самостоятельное изучение нового материала, усвоение которого проверяет учитель в беседе с классом. При закреплении материала, отработке умений и навыков ученик вновь работает индивидуально, сам выбирая уровень сложности и темп своей работы. Правила работы с дидактическим материалом (карточки с задачами или задачи из учебника): все теоретические вопросы должны быть пропущены через самостоятельную работу и рассмотрены всесторонне; повторение ранее изученного «вклинивается» в новый материал; соблюдение принципа первоначального успеха - первые задания должны быть заведомо выполнимыми, чтобы ребенок получил стимул для дальнейшей деятельности (именно такие задачи и предлагаются обучающимся на данном уроке.) Учитель выполняет на уроке роль консультанта и организатора деятельности детей, что способствует увеличению времени активной работы учащихся на уроке и его эффективности.
Урок алгебры в 8 классе по теме :
«Определение квадратного уравнения. Неполные квадратные уравнения»
Цель.
В конце занятия обучающиеся должны знать определение квадратного уравнения и уметь пользоваться терминологией, связанной с ним, овладеть умением различать неполные квадратные уравнения и решать неполные квадратные уравнения трех видов.
Развивать умения: работать самостоятельно с учебной литературой, анализировать свою работу, умение классифицировать, сравнивать, сопоставлять; развивать математическую речь, познавательную активность.
Воспитывать интерес к математике, культуру поведения.
Оборудование: карточки для устного счета, карточки-инструкции, портрет Аль-Хорезми, проектор.
Ход урока.
І. Организация начала урока: приветствие, постановка целей урока.
ІІ. Актуализация опорных знаний.
Прежде чем приступить к изучению новой темы, учитель предлагает обучающимся вспомнить известные им свойства арифметического квадратного корня, решив примеры, представленные на экране. Особо отмечается то, что дети не просто решат примеры, а расшифруют имя узбекского математика и астронома IX века, который внес существенный вклад в развитие математической науки. Каждый ответ в примере соответствует номеру буквы на карточке, и, записав найденные буквы, можно прочесть имя. Карточки с расшифровкой букв раздаются каждому ученику, дети работают индивидуально, присутствует элемент состязательности.
Примеры:
1. 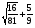 ; 6.
; 6. 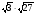 ;
;
2.  ; 7.
; 7.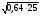 ;
;
3. 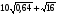 ; 8.
; 8. 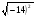 ;
;
4. 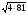 ; 9.
; 9. 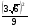 ;
;
5. 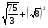 ; 10.
; 10. 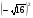 .
.
Образец карточки.
1
2
3
4
5
6
7
8
9
А
Д
Д
Е
К
М
Н
П
Р
10
11
12
13
14
15
16
17
18
Т
Л
Ь
О
З
Ф
И
Я
Х
Решение: Аль-Хорезми.
ІІІ. Историческая справка: рассказ, заранее подготовленный одним из учеников. На экране перед классом - портрет Аль-Хорезми.
Аль-Хорезми известен тем, что написал основополагающий трактат по алгебре. Трактат был посвящен решению уравнений, иученый рассматривал этот вопрос как самостоятельную науку. В книге Аль-Хорезми речь шла о двух важнейших операциях, необходимых при решении уравнений: переносе членов уравнения с одной стороны знака равенства в другую и о приведении подобных членов уравнения. Собственно, от названия трактата произошло слово «Алгебра». В книге содержались решения уравнений первой и второй степени таких видов: 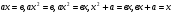 .(уравнения представлены на экране).
.(уравнения представлены на экране).
Хорезми приводил и геометрические способы решения таких уравнений. Его книга пользовалась большой популярностью, а в математике осталось и имя автора в латинизированном виде: алгоритм. Теперь это слово обозначает всякую систему вычислений , производимых по строго определенным правилам и заведомо приводящих к решению поставленной задачи. Хорезми не высказывал мысли о своем приоритете в алгебре. Видимо, оба приема - перенос членов уравнения и приведение подобных - были уже широко известны в его время.
А теперь ваша очередь познакомиться с тем, что такое квадратное уравнение и выяснить, как решаются некоторые виды квадратных уравнений.
ІV. Изучение нового материала.
Теоретические положения темы изучаются самостоятельно при помощи карточек-инструкций. На одной стороне карточки записаны вопросы, на которые должен ответить ученик (можно письменно, но кратко), а на другой для самоконтроля даны ответы на эти вопросы.
Образец карточки
Вопросы.
Использую учебник («Алгебра. 8 класс»/ А.Г. Мордкович), ответьте на следующие вопросы.
-
Какое уравнение называется квадратным?
-
Придумайте и запишите квадратное уравнение.
-
Как называются числа а, в и с?
-
Какие квадратные уравнения называются неполными?
-
Какие встречаются виды неполных квадратных уравнений?
-
Придумайте и запишите неполное квадратное уравнение каждого вида.
В СЛУЧАЕ ЗАТРУДНЕНИЙ, ИЛИ ЕСЛИ ВАШИ ОТВЕТЫ НЕ СОВПАДУТ С ОТВЕТАМИ НА ОБРАТНОЙ СТОРОНЕ КРТОЧКИ, - ПОДНИМИТЕ РУКУ.
Ответы.
-
Уравнение вида
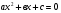 , где х - переменная,
, где х - переменная, 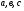 - некоторые числа, причем а≠0.
- некоторые числа, причем а≠0. -
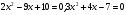 и т.д.
и т.д. -
а -первый коэффициент, в - второй коэффициент, с -свободный член уравнения.
-
Уравнения, в которых хотя бы один из коэффициентов в или с равен 0.
-
ах2=0, ах2 + вх = 0 (в≠0), ах2 + с = 0 (с≠0).
-
4х2=0, 4х2 + 8х =0, 4х2 - 12 =0.
V. Проверка уровня усвоения теоретического материала. (фронтальная работа с классом)
1. Укажите среди представленных на экране уравнения первой степени и квадратные.
5х - 2 = 0, 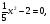
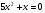 ,
,
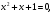
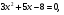
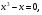
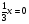 .
.
2. Чему равен первый и второй коэффициенты уравнения, его свободный член?
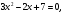
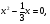
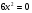 ,
,
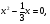
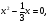
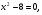 .
.
Назовите среди данных уравнений неполные.
VІ. Составление алгоритма решения неполных квадратных уравнений
В ходе беседы с учениками, путем рассуждений, опираясь на имеющиеся знания и опыт решения уравнений первой степени, не используя учебник, учитель вместе с классом выводит алгоритм решения неполных квадратных уравнений на конкретных примерах. В ходе этой работы в тетрадях учеников появляется следующая запись, которой они будут пользоваться, как опорой.
ах2= 0
ах2 +вх = 0
ах2 +с = 0
6х2=0,
х2=0,
х = 0.
Ответ: 0.
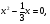
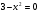
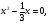 или
или 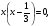 =0,
=0,
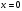 .
.
Ответ: 0, 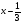
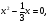
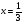
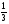 ,
,
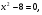 .
.
Ответ: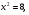 .
.
VІІ. Первичное закрепление нового материала в форме обучающей самостоятельной работы.
Используя образцы решения, дети самостоятельно решают задачи из учебника: § 24.
Учитель играет роль консультанта, проверяя задачи и помогая тем, кто затрудняется решить.
VІІІ. Итог урока: обсуждение результатов сделанного на уроке, домашнее задание.