- Учителю
- Урок математики по теме 'Прямая и обратная пропорциональные зависимости' (6 класс)
Урок математики по теме 'Прямая и обратная пропорциональные зависимости' (6 класс)
Тема урока: «Прямая и обратная пропорциональные зависимости».
6 класс
Учитель: Суслова Т.В.
Всего на изучение темы отводится 4 часа, этот урок 3.
Цели урока:
-
Дидактическая: закрепление знания понятий прямо и обратно пропорциональных величин; закрепление навыков решения задач, связанных с прямо и обратно пропорциональными величинами; закрепление навыков и умений решения пропорций.
-
Развивающая: развитие мыслительной деятельности обучающихся, фантазии детей и их способности рассуждать, ставить вопросы и отвечать на них, т.е. развитие математической речи, умения говорить красиво, грамотно, чётко, в нужном темпе.
-
Воспитательная: воспитание аккуратности выполнения записей на доске и в тетрадях, формирование любознательности, пробуждение интереса ко всему, что нас окружает, расширение кругозора при решении старинных практических (или правдоподобных) задач.
Ход урока:
-
Организационный момент.
-
приветствие учащихся; проверка их готовности к уроку;
-
сообщение темы, цели - повторим то, что необходимо знать при решении задач на прямую и обратную пропорциональные зависимости, проверим свои умения решать такие задачи в с/р;
-
Д/з на следующий урок: решить задачи (текст на карточках), составить кроссворд по вопросам к п. 20-22.
-
Проверка Д/з.
Дома надо было составить две задачи на прямую и обратную пропорциональные зависимости. 2 человека к доске по 1 задаче (показать решение).
Отвечающим вопросы по теме урока (задают учащиеся).
-
Во время устной работы задания на карточках:
карточка № 1. Решите уравнения:
1) ![]() Ответ. 6. 3)
Ответ. 6. 3) ![]() Ответ.
Ответ. ![]() .
.
2) ![]() Ответ.
Ответ. ![]() . 4)
. 4) ![]() Ответ. 0,5.
Ответ. 0,5.
карточка № 2. Решите уравнения:
1) ![]() Ответ. 8. 3)
Ответ. 8. 3) ![]() Ответ.
Ответ. ![]() .
.
2) ![]() Ответ.
Ответ. ![]() . 4)
. 4) ![]() Ответ.
Ответ. ![]() .
.
-
Устно.
На доске записаны равенства:
-
3 : 7 = 6 : 14 В 4)
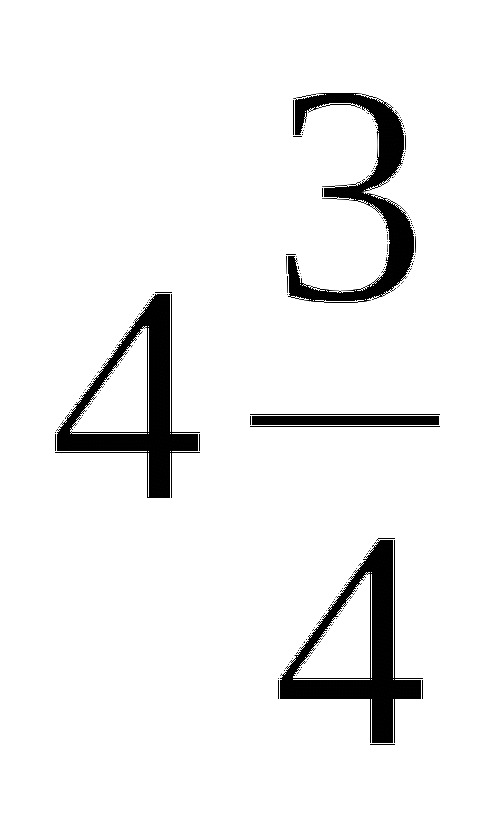
-
3 : 12 = 1 4 5)
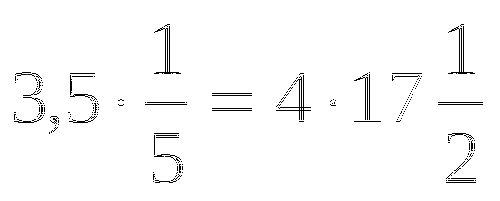 В
В -
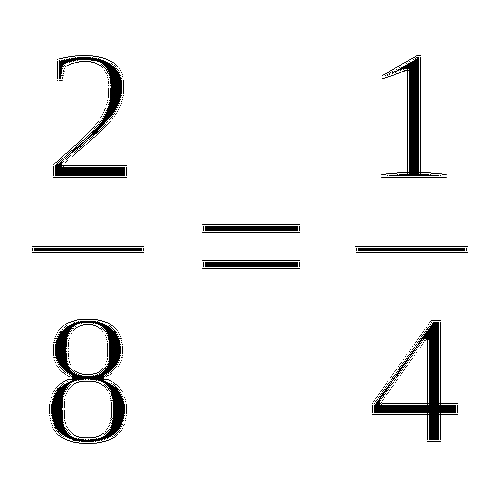 В 6)
В 6) 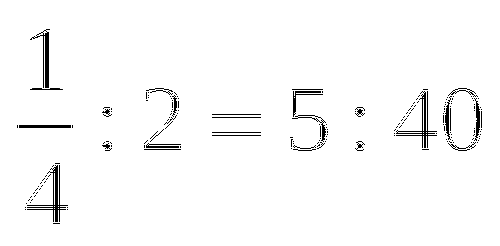
Вопросы:
-
Какие из данных равенств являются пропорциями? Что такое пропорция? Назовите крайние и средние члены в данных пропорциях.
-
Какие из данных пропорций являются верными? Как проверить верность пропорции? Сформулируйте основное свойство пропорции.
-
Как найти неизвестный крайний член пропорции? неизвестный средний?
-
Какие величины называют прямо пропорциональными? обратно пропорциональными?
-
Определите, является ли прямо пропорциональной, обратно пропорциональной или не является пропорциональной зависимость между величинами:
- путь, пройденный а/м с постоянной скоростью, и время ее движения;()
- скорость и время движения а/м;()
- стоимость товара, купленного по одной цене и его количеством;()
- цена товара и его количество, купленное на одну и туже сумму денег;()
- число рабочих, выполняющих с одинаковой производительностью труда некоторую работу, и временем выполнения этой работы;()
- возраст дерева и его высота;(-)
- возраст человека и его размер обуви;(-)
- число прочитанных страниц в книге и число страниц, которые осталось прочитать (Вася прочитал 10 страниц, ему осталось прочитать 90 страниц. Сколько ему останется прочитать страниц, когда он прочитает 30 страниц?);(-)
- За 2 часа поймали 12 карасей. Сколько карасей поймают за 3 часа?
- Три петуха разбудили 6 человек. Сколько человек разбудят 5 петухов?
-
С/р (тест). Ответы пишутся на листках с заданиями. По окончанию работы взаимопроверка с выставлением отметки.
I вариант.
1. Вставьте пропущенные слова. Чтобы найти неизвестный крайний член пропорции, надо произведение ______________ членов пропорции разделить на известный ______________ член.
2. Составьте пропорцию для решения задачи.
1) Принтер распечатывает 27 страниц за 4,5 мин. За сколько времени он распечатает 300 страниц?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2) Определенную работу 8 человек выполняли за 25 дней. За сколько дней эту же работу выполнят 10 человек, работая с той же производительностью.
а) 8 : 10 = 25 : х; б) 8 : 10 = х : 25; в) 8 : 25 = 10 : х.
3. Дополнительно. Решите задачу.
Четыре класса построили снежную горку за 5 дней. За сколько дней выполнят ту же работу 10 классов, если будут работать с такой же производительностью?
II вариант.
1. Вставьте пропущенные слова. Чтобы найти неизвестный средний член пропорции, надо произведение ______________ членов пропорции разделить на известный ______________ член.
2. Составьте пропорцию для решения задачи.
1) В двух литрах раствора содержится 10гр. соли. Сколько соли в 7 литрах этого раствора?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2) В коробке 48 пачек чая по 250 г в каждой. Сколько получится из этого чая пачек по 150г?
а) 48 : х = 150 : 250; б) 48 : х = 250 : 150; в) х : 48 = 150 : 250.
3. Дополнительно. Решите задачу.
Для приготовления вишневого варенья на 3 стакана вишни берут 2 стакана сахара. Сколько надо взять сахара, чтобы сварить варенье из двух стаканов вишни?
Ответы: I вариант. 1. средних, крайний. 2. 1) - б); 2) - б). 3. 2 дня.
II вариант. 1. крайних, средний. 2. 1) - а); 2) - а). 3. ![]() .
.
-
На доске решить задачи.
1) Взяли 560 человек солдат корма на 7 месяцев, а приказано им на службе быть 10 месяцев, и захотели людей от себя убавить, чтобы корма хватило на 10 месяцев. Спрашивается, сколько человек надо убавить? (168 солдат надо убавить)
2) 8 аршин сукна стоит 30 рублей. Сколько стоит 15 аршин этого сукна? (56,25 р.)
-
С/р по вариантам. Решение в тетради.
I вариант.
1. Автомобиль проехал 3 часа со скоростью 60 км/ч. За сколько часов он проедет то же расстояние, если будет ехать со скоростью 45 км/ч? Ответ: 4 часа.
2. Зная, что величины, указанные в краткой записи задачи обратно пропорциональные, составьте пропорцию и решите задачу.
6 машин - 12тыс. руб.
x машин - 18 тыс. руб. Ответ: 4 машины.
II вариант.
1.Горнорудному предприятию требуется закупить на определённую сумму денег 5 новых машин по цене 12 тыс. руб. за одну. Сколько таких машин сможет купить предприятие, если цена за одну машину станет 15 тыс. рублей? Ответ: 4 машины.
2. Зная, что величины, указанные в краткой записи задачи, обратно пропорциональны, составьте пропорцию и решите задачу.
180 дней - по 0,6т угля в день
x дней - по 0,5т угля в день Ответ: 216 дней.
III вариант.
1. Зная, что величины, указанные в краткой записи задачи, прямо пропорциональны, составьте пропорцию и решите задачу.
5 дет. - 12 дней
4 дет. - х дней Ответ: ![]() дней.
дней.
2. Зная, что величины, указанные в краткой записи задачи, обратно пропорциональны, составьте пропорцию и решите задачу.
4 часа - 3км/ч
х часов - 2км/ч Ответ: 6 часов.
-
Задачи на смекалку и внимание. (Для тех, кто раньше остальных справится с с/р). Каждому верному ответу соответствует буква. Какое слово получилось?
7 - В, 10 - У, 90 - К, 6 - Р, 4 - Е, 9 - Н, 11 - Л, 5 - А. Ответ: ВАНКУВЕР.
1) Определите, сколько треугольников вы видите на рис.1 и квадратов на рис.2а,б?
2) . 22=4, 32=9, а угол в квадрате? (900).
3) На угол в 10 смотрят в увеличительное стекло с пятикратным увеличением. Чему равен угол в увеличительном стекле? (10).
4) Петух на одной ноге весит 4 кг. А на двух? (4 кг)
5) В семье 5 сыновей и у каждого есть сестра. Сколько детей в семье? (6 чел.)
6) Бревно распилили на 8 частей. Сколько распилов сделали? (7 распилов)
IX. Итоги урока.
- Что нового вы узнали на уроке?
- Что повторили?
- Каков алгоритм решения задач на пропорцию?
- Мы достигли поставленной цели?
- Как оцениваете свою работу?
Д/з на следующий урок: тем, кто имеет оценку «4 и 5» решить задачи 2 и 3, остальным - решить задачи 1 и 2; всем составить кроссворд.
1) При сжигании 1кг горючего в воздух автомобилем выбрасывается 0,8кг угарного газа. Сколько угарного газа будет выброшено автомобилем при сжигании 50кг горючего? (Ответ: 40 кг)
2) Нормальное содержание гемоглобина в крови у взрослого человека составляет примерно 130 грамм на 1 литр. На сколько процентов понизился гемоглобин, если он составляет 78 грамм на 1 литр? (Ответ: на 40%)
3) Некий господин позвал плотника и велел двор построить. Дал ему 20 человек работников и спросил, во сколько дней построят они ему двор. Плотник ответил: в 30 дней. А господину надобно в 5 дней построить, и ради того спросил он плотника: сколько человек тебе надо иметь, дабы с ними ты построил двор в 5 дней; и плотник, недоумевая, спрашивает тебя, арифметик: сколько человек ему надо нанять, чтобы построить двор в 5 дней?
(Ответ: 120 работников)
6