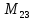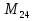- Учителю
- Творческая работа ученика 8 класса по теме'Числа Мерсенна'
Творческая работа ученика 8 класса по теме'Числа Мерсенна'
Министерство образования и науки, молодежи и спорта Автономной Республики Крым
Гпавное управление образования и науки Сакской райгосадминистрации
Сакское территориальное отделение МАН Украины
Секция математики
Сакский районный филиал
ЧИСЛА МЕРСЕННА
Работу выполнил
Айсинов Иван, учащийся 8 класса, кдч
(Сакский район, Митяевская ОШ)
Научный руководитель
Будякова Л.В. учитель математики
Митяевской ОШ
с. Митяево-2012г.
Математика, как и большинство современных наук, в настоящее время развивается со все возрастающей скоростью. В мире выходят сотни математических журналов, в которых публикуется много научных работ. А более трехсот семидесяти лет назад никаких математических журналов, а тем более Интернета, еще не было, и ученые обменивались результатами своих исследований в личных письмах. Правда, был один человек- французский монах Марен Мерсенн, живший в 1588-1648 годах, который получал таких писем больше других. Написать об открытии новой теоремы Мерсенну означало установить свой приоритет, поскольку Мерсенн, как правило сообщал об этом остальным своим корреспондентам, в числе которых были Р. Декарт, Б. Паскаль, П. Ферма, Х. Гюйгенс и многие другие ученые того времен.
Я нашел в книге »История математики» упоминание о простых числах, совершенных числах. Заинтересовался этим вопросом, прочитал еще некоторые книги и журналы, где содержалось упоминание о числах Мерсенна.
Изучил геометрическую прогрессию из курса 9 класса.
Вычислил некоторые из чисел Мерсенна и обнаружил закономерность, затем доказал, что числа вида 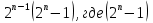 - простое число Мерсенна, -это совершенные числа. Это такие замечательные числа.
- простое число Мерсенна, -это совершенные числа. Это такие замечательные числа.
Марен Мерсенн родился в крестьянской семье 8.09.1588году, в посёлке Уазе; в наши дни это департамент Сарта. Учился в иезуитском коллеже в Ла-Флеш, вместе с Декартом, тесную дружбу с которым Мерсенн пронёс через всю жизнь.
В 1611 году Мерсенн присоединился к францисканскому ордену «минимов». Далее он продолжил обучение в Париже. В 1613 году был рукоположен в священники, но не прекратил обучения, занявшись математикой, музыкой и философией. Совершил несколько путешествий по Европе, побывал в Италии, Германии, Голландии и других странах. Во время поездок приобретал новые знакомства, завязывал переписку, слушал лекции в местных университетах. Затем Мерсенн вернулся в Париж, поселился в монастыре и последующие десятилетия отдал науке и преподаванию философии.
Став до некоторой степени центральной фигурой, объединяющей учёных разных стран в области физико-математических наук, своей деятельностью Мерсенн выполнял, в ограниченных, конечно, размерах, функции не существовавшей ещё в его время Парижской Академии наук. В течение его продолжительного пребывания в Париже у него еженедельно происходили собрания математиков и физиков, с целью взаимного обмена идеями и мыслями, а также информирования о результатах предпринятых исследований (четверги Мерсенна). Позднее из этого кружка образовалась, при содействии Кольбера, Парижская Академия наук (1666).
На протяжении первой половины XVII века Марен Мерсенн был по существу координатором научной жизни Европы, ведя активную переписку практически со всеми видными учёными того времени. Эта переписка имеет огромную научную и историческую ценность. Имеет также серьёзные личные научные заслуги в области математики, акустики и теории музыки.
Мерсенн вёл чрезвычайно оживлённую переписку (на латинском языке), представляющую громадный исторический интерес. В числе его 78 корреспондентов, кроме Декарта, были Галилей, Кавальери, Паскаль, Роберваль, Торричелли, Ферма, Гюйгенс, Гассенди, Дж. Б. Дони и многие другие. Научная периодика тогда не существовала, и деятельность Мерсенна значительно способствовала быстрому прогрессу физико-математических наук. 17-томное собрание переписки Мерсенна было издано в Париже в 1932-1988 годах. Умер 1.09.1648году, не дожил до 60-летия семи дней.
Эта деятельность Марена Мерсенна способствовала созданию в Париже Академии наук.
Я заинтересовался деятельностью Марена Мерсенна, решил заняться этим вопросом и обнаружил в его работе необыкновенные числа, которые впоследствии стали называться числами Мерсенна.
Из собственных математических достижений Мерсенна наибольшей популярностью пользуются изученные им числа вида 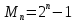 .
.
Тот, кто знает, что такое геометрическая прогрессия, сразу заметит, что 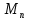 равняется сумме первых n членов геометрической прогрессии с первым членом
равняется сумме первых n членов геометрической прогрессии с первым членом 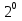 = 1 и знаменателем 2:
= 1 и знаменателем 2:
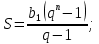
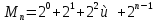
Мерсенна интересовало, какие из чисел 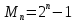 являются простыми, то есть такие натуральные числа, которые имеют два натуральных делителя.
являются простыми, то есть такие натуральные числа, которые имеют два натуральных делителя.
Вопрос этот возник в задаче, поставленной еще древними грекам. Они занимались совершенными числами- числами, равными сумме всех своих натуральных делителей, отличных, конечно же, от самого числа. Например, 6=1+2+3, 28=1+2+4+7+14, 496=1+2+4+8+16+31+62+124+248 - первые три совершенных числа.
Простые числа, получающиеся по формуле 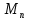 =
=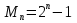 , и называются числами Мерсенна.
, и называются числами Мерсенна.
Попробовал и я коснуться проблемы поиска чисел Мерсенна. Вычислил несколько первых чисел по формуле и записал их по порядку в таблицу из четырех столбиков.
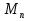 = 1
= 1
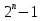 = 31
= 31
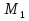 = 511
= 511
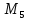 = 8.191
= 8.191
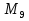 = 131.071
= 131.071
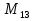 = 2.997.151
= 2.997.151
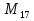 = 33.554.431
= 33.554.431
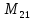 = 536.870.911
= 536.870.911
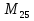
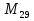
 = 3
= 3
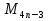 = 63
= 63
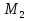 = 1.023
= 1.023
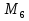 = 16.383
= 16.383
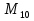 = 262.143
= 262.143
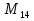 = 4.194.303
= 4.194.303
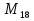 = 67.108.863
= 67.108.863
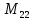 = 1.073.741.823
= 1.073.741.823
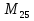
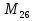
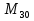 = 7
= 7
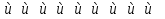 = 127
= 127
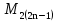 = 2.047
= 2.047
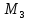 = 32.767
= 32.767
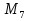 = 524.287
= 524.287
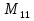 = 8.388.607
= 8.388.607
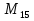 = 134.217.727
= 134.217.727
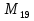 = 2.147.483.647
= 2.147.483.647
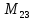
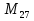
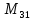 = 15
= 15
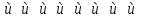 = 255
= 255
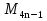 = 4.095
= 4.095
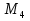 = 65.535
= 65.535
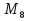 = 1.048.575
= 1.048.575
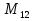 = 16.777.215
= 16.777.215
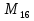 = 268.435.455
= 268.435.455
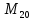 =4.294.967.295
=4.294.967.295
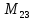
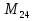
Первое наблюдение: числа, попадающие в один и тот же столбец, оканчиваются на одну и ту же цифру. А именно, числа, попадающие в первый столбец, оканчиваются на 1, во второй столбец - на 3, в третий столбец - на 7, а в третий - на 5. Это обусловлено тем, что первая степень числа 2 оканчивается цифрой 2, вторая - цифрой 4, третья - цифрой 8, четвертая - цифрой 6, а дальше идет повторение 2, 4, 8, 6, ровно через 4, а если вычесть 1, то и получатся цифры 1, 3, 7, 5. Значит, числа 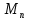 , попадающие в четвертый столбец делятся на 5, и среди них не может быть чисел Мерсенна.
, попадающие в четвертый столбец делятся на 5, и среди них не может быть чисел Мерсенна.
Несложно доказать и второе наблюдение: числа, попадающие во второй столбец делятся на 3. В самом деле, числа 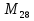 при k=1равно 3 и делится на 3, допустим, что
при k=1равно 3 и делится на 3, допустим, что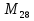 делится на 3, докажем, что и
делится на 3, докажем, что и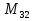 делится на3. Составим разность
делится на3. Составим разность 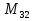 и
и 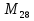 :
:
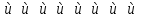
Разность и одно из чисел делится на3, значит, и второе число тоже делится на 3. Поэтому, если число 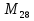 делится на 3, то и число
делится на 3, то и число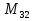 делится на 3 по принципу математической индукции.
делится на 3 по принципу математической индукции.
Поэтому числа Мерсенна (за исключением 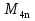 =3) имеет смысл искать в первом и третьем столбцах.
=3) имеет смысл искать в первом и третьем столбцах.
Более пристальное изучение чисел 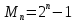 приводит к третьему наблюдению: если n - составное число,
приводит к третьему наблюдению: если n - составное число, 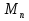 , то
, то 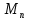 делится на
делится на 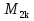 и на
и на 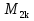 . Это следует из того, что
. Это следует из того, что 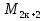 , а
, а 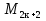 . Кстати, из третьего наблюдения вытекают и первые два, поскольку все числа из второго столбца делятся на 3, а в четвертом делятся на 5.
. Кстати, из третьего наблюдения вытекают и первые два, поскольку все числа из второго столбца делятся на 3, а в четвертом делятся на 5.
Итак, число 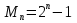 будет простым только при условии, что n - простое.
будет простым только при условии, что n - простое.
Но для любого ли простого р число 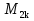 , будет простым? Надежда на положительный ответ рушится очень быстро: уже число
, будет простым? Надежда на положительный ответ рушится очень быстро: уже число 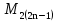 =2047=23
=2047=23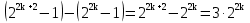 89 является составным.
89 является составным.
Сам Мерсенн указал все простые значения n, не превосходящие 257, для которых, по его мнению, числа 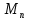 =
=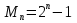 будут простыми. Однако Мерсенн не дал доказательства; впоследствии выяснилось, что его предположение оказалось частично ошибочным.
будут простыми. Однако Мерсенн не дал доказательства; впоследствии выяснилось, что его предположение оказалось частично ошибочным.
И снова вернемся к так называемым совершенным числам. Еще Евклид доказал, что ели число 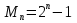 простое, то число
простое, то число 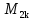 - совершенное. Леонард Эйлер доказал, что все четные совершенные числа имеют вид
- совершенное. Леонард Эйлер доказал, что все четные совершенные числа имеют вид 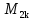 , где
, где 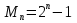 - число Мерсенна.
- число Мерсенна.
Я докажу это. Выпишу все делители этого числа: 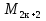 .
.
Найду их сумму: 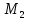 )
)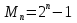 Значит,
Значит, 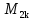 - число совершенное.
- число совершенное.
Поисками чисел Мерсенна занимался и Леонард Эйлер, член Петербургской Академии наук, один из величайших математиков Нового времени. В 1750 году он обнаружил десятое по счету число Мерсенна; это 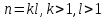
Если раньше поиск чисел Мерсенна велся "кустарным и" методами, то в 20 и21 веках в работу включилась ЭВМ, считающие с огромной скоростью. В 1952 сразу было найдено пять новых чисел Мерсенна: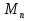 ; они являются соответственно тринадцатым- семнадцатым числами Мерсенна. Следующие числа были найдены в период с 1957 года по 1963 год. Наконец, в 1971 году найдено 24-е число
; они являются соответственно тринадцатым- семнадцатым числами Мерсенна. Следующие числа были найдены в период с 1957 года по 1963 год. Наконец, в 1971 году найдено 24-е число 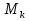 . В 1978 году - 25-е число
. В 1978 году - 25-е число 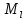 , в 1979году - 26-е и 27-е числа
, в 1979году - 26-е и 27-е числа 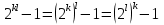 . До настоящего времени были известны только 44 числа Мерсенна, последнее из которых 232582657 - 1 было найдено еще в 2006 г. тоже участниками Great Internet Mersenne Prime Search. Независимые эксперты подтвердили нахождение 45-го и 46-го по счету известных человечеству чисел Мерсенна в 2008 году.
. До настоящего времени были известны только 44 числа Мерсенна, последнее из которых 232582657 - 1 было найдено еще в 2006 г. тоже участниками Great Internet Mersenne Prime Search. Независимые эксперты подтвердили нахождение 45-го и 46-го по счету известных человечеству чисел Мерсенна в 2008 году.
В наши дни Мерсенн известен более всего как исследователь «чисел Мерсенна», играющих важную роль в теории чисел, криптографии и генераторах псевдослучайных чисел. Большие простые числа используются в криптографии с открытым ключом. Простые числа также используются в хеш-таблицах и для генерации псевдослучайных чисел Атака «человек посередине»- термин в криптографии, обозначающий ситуацию, когда атакующий способен читать и видоизменять по своей воле сообщения, которыми обмениваются корреспонденты, причём ни один из последних не может догадаться о его присутствии в канале.
В криптографии, протокол поиска информации (PIR) позволяет потребителю (или игроку) получить интересующую его частную информацию с сервера. Причём сервер не сможет распознать какая именно часть его информации стала известна игроку. Задача : Есть база данных состоящая из битов. Есть игрок, который хочет достать бит номер так, чтобы база данных содержащая все битов не смогла узнать никакой информации какой именно бит достал игрок. Тривиальное (но не эффективное) решение состоит в посылке всех битов игроку, включая искомый им бит. Другой путь - использование PIR-протокола где игрок задаёт вопрос (функцию) базе данных. Последняя берёт эту функцию, прилагает её ко всей совокупности базы данных и получает ответ, который высылается обратно игроку. Условия этой игры следующие:
1) Длина суммы вопроса (функции) и ответа должна быть много меньше чем n.
2) игрок должен для любого бита послать такой вопрос, чтобы ответ был правильный, то есть бит был верно получен.
3) База данных не может ничего узнать по поводу этого игрока.
Литература.
-
И.Н.Виноградов И.Н.Математическая энциклопедия.- М.: Советская энциклопедия. 1977.- с.123.
-
Глейзер Г.И. История математики в школе 7-9кл.-М.: Просвещение,1983.
-
О.М.Мамедов. Числа Мерсенна. //Журнал «Квант» №10, 1986г.-с.24-25.
-
П.П.Орлов. Новые методики решения задач о числах. -М.: изд-во Либроком,2011.-с. 34-37.
-
Яковлев. А. Я. Леонард Эйлер.-М.: Изд-во «Просвещение»,1983.-с.41-42.
-
Ю.В.Королев.: Совершенные числа. //Журнал «Квант» №6, 1972г.- с.27-28.

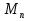 = 1
= 1
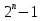 = 31
= 31
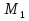 = 511
= 511
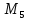 = 8.191
= 8.191
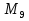 = 131.071
= 131.071
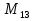 = 2.997.151
= 2.997.151
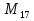 = 33.554.431
= 33.554.431
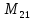 = 536.870.911
= 536.870.911
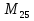
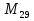
 = 3
= 3
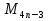 = 63
= 63
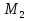 = 1.023
= 1.023
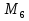 = 16.383
= 16.383
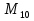 = 262.143
= 262.143
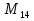 = 4.194.303
= 4.194.303
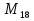 = 67.108.863
= 67.108.863
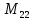 = 1.073.741.823
= 1.073.741.823
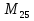
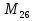
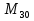 = 7
= 7
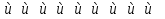 = 127
= 127
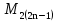 = 2.047
= 2.047
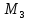 = 32.767
= 32.767
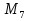 = 524.287
= 524.287
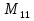 = 8.388.607
= 8.388.607
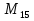 = 134.217.727
= 134.217.727
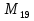 =2.147.483.647
=2.147.483.647
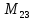
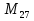
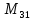 = 15
= 15
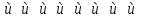 = 255
= 255
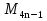 = 4.095
= 4.095
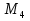 = 65.535
= 65.535
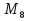 = 1.048.575
= 1.048.575
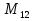 = 16.777.215
= 16.777.215
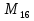 = 268.435.455
= 268.435.455
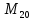 =4.294.967.295
=4.294.967.295