- Учителю
- Рабочая программа по математике 5-9 классы по ФГОС
Рабочая программа по математике 5-9 классы по ФГОС
Муниципальное бюджетное общеобразовательное учреждение
«Большечурашевская средняя общеобразовательная школа»
Ядринского района Чувашской Республики«Рассмотрено»
руководитель ШМО
________ Андреева Р.П.
Протокол № ___ от
«___»____________2016 г
«Согласовано»
Заместитель директора школы по УВР МБОУ «Большечурашевская СОШ»
____________Сергеева В.Ю
«____»____________2016 г.
«Утверждено»
Директор МБОУ
«Большечурашевская СОШ»
__________ Викторов В.Г.
Приказ № _____ от «___» августа 2016 г.
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
курса «математика»
на 2016-2017 учебный год
Учитель математики
первой категории
Архипова Ирина Валериановна
с. Большое Чурашево - 2016
Пояснительная записка.
Рабочая программа основного общего образования по математике для 5-9 классов составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. А также Примерной основной образовательной программы основного общего образования, Сборника рабочих программ. 5-6 классы. Математика: пособие для учителей общеобразоват. организаций / [сост. Т. А. Бурмистрова]. - 3-е изд. - М.: Просвещение, 2014. - 80 с., Сборника рабочих программ. 7-9 классы Алгебра : пособие для учителей общеобразоват. организаций / [составитель Т. А. Бурмистрова]. - 2-е изд., доп. - М.: Просвещение, 2014. - 96 с, Сборника рабочих программ. 7-9 классы. Геометрия: пособие для учителей общеобразоват. организаций / [сост. Т. А. Бурмистрова]. - 2-е изд., дораб. - М.: Просвещение, 2014. - 95 с.
Согласно Федеральному базисному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится не менее 870 часов из расчёта 5 учебных часов в неделю в 5-9 классах.
В соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования предмет «Математика» изучается с 5-го по 9-й класс в виде следующих учебных курсов: 5-6 класс - «Математика» (интегрированный предмет), 7-9 классах предмет «Математика» (Алгебра и Геометрия). Базовый уровень.
Планируемые результаты освоения учебного предмета, курса
Выпускник научится в 5-6 классах (для использования в повседневной жизни и обеспечения возможности успешного продолжения образования на базовом уровне)
-
Оперировать на базовом уровне1 понятиями: множество, элемент множества, подмножество, принадлежность;
-
задавать множества перечислением их элементов;
-
находить пересечение, объединение, подмножество в простейших ситуациях.
В повседневной жизни и при изучении других предметов:
-
распознавать логически некорректные высказывания.
Числа
-
Оперировать на базовом уровне понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число;
-
использовать свойства чисел и правила действий с рациональными числами при выполнении вычислений;
-
использовать признаки делимости на 2, 5, 3, 9, 10 при выполнении вычислений и решении несложных задач;
-
выполнять округление рациональных чисел в соответствии с правилами;
-
сравнивать рациональные числа.
В повседневной жизни и при изучении других предметов:
-
оценивать результаты вычислений при решении практических задач;
-
выполнять сравнение чисел в реальных ситуациях;
-
составлять числовые выражения при решении практических задач и задач из других учебных предметов.
Статистика и теория вероятностей
-
Представлять данные в виде таблиц, диаграмм,
-
читать информацию, представленную в виде таблицы, диаграммы.
Текстовые задачи
-
Решать несложные сюжетные задачи разных типов на все арифметические действия;
-
строить модель условия задачи (в виде таблицы, схемы, рисунка), в которой даны значения двух из трех взаимосвязанных величин, с целью поиска решения задачи;
-
осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию;
-
составлять план решения задачи;
-
выделять этапы решения задачи;
-
интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;
-
знать различие скоростей объекта в стоячей воде, против течения и по течению реки;
-
решать задачи на нахождение части числа и числа по его части;
-
решать задачи разных типов (на работу, на покупки, на движение), связывающих три величины, выделять эти величины и отношения между ними;
-
находить процент от числа, число по проценту от него, находить процентное отношение двух чисел, находить процентное снижение или процентное повышение величины;
-
решать несложные логические задачи методом рассуждений.
В повседневной жизни и при изучении других предметов:
-
выдвигать гипотезы о возможных предельных значениях искомых величин в задаче (делать прикидку)
Наглядная геометрия
Геометрические фигуры
-
Оперировать на базовом уровне понятиями: фигура, точка, отрезок, прямая, луч, ломаная, угол, многоугольник, треугольник и четырехугольник, прямоугольник и квадрат, окружность и круг, прямоугольный параллелепипед, куб, шар. Изображать изучаемые фигуры от руки и с помощью линейки и циркуля.
В повседневной жизни и при изучении других предметов:
-
решать практические задачи с применением простейших свойств фигур.
Измерения и вычисления
-
выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;
-
вычислять площади прямоугольников.
В повседневной жизни и при изучении других предметов:
-
вычислять расстояния на местности в стандартных ситуациях, площади прямоугольников;
-
выполнять простейшие построения и измерения на местности, необходимые в реальной жизни.
История математики
-
описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;
-
знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей.
Выпускник получит возможность научиться в 5-6 классах (для обеспечения возможности успешного продолжения образования на базовом и углубленном уровнях)
Элементы теории множеств и математической логики
-
Оперировать2 понятиями: множество, характеристики множества, элемент множества, пустое, конечное и бесконечное множество, подмножество, принадлежность,
-
определять принадлежность элемента множеству, объединению и пересечению множеств; задавать множество с помощью перечисления элементов, словесного описания.
В повседневной жизни и при изучении других предметов:
-
распознавать логически некорректные высказывания;
-
строить цепочки умозаключений на основе использования правил логики.
Числа
-
Оперировать понятиями: натуральное число, множество натуральных чисел, целое число, множество целых чисел, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число, множество рациональных чисел, геометрическая интерпретация натуральных, целых, рациональных;
-
понимать и объяснять смысл позиционной записи натурального числа;
-
выполнять вычисления, в том числе с использованием приемов рациональных вычислений, обосновывать алгоритмы выполнения действий;
-
использовать признаки делимости на 2, 4, 8, 5, 3, 6, 9, 10, 11, суммы и произведения чисел при выполнении вычислений и решении задач, обосновывать признаки делимости;
-
выполнять округление рациональных чисел с заданной точностью;
-
упорядочивать числа, записанные в виде обыкновенных и десятичных дробей;
-
находить НОД и НОК чисел и использовать их при решении зада;.
-
оперировать понятием модуль числа, геометрическая интерпретация модуля числа.
В повседневной жизни и при изучении других предметов:
-
применять правила приближенных вычислений при решении практических задач и решении задач других учебных предметов;
-
выполнять сравнение результатов вычислений при решении практических задач, в том числе приближенных вычислений;
-
составлять числовые выражения и оценивать их значения при решении практических задач и задач из других учебных предметов.
Уравнения и неравенства
-
Оперировать понятиями: равенство, числовое равенство, уравнение, корень уравнения, решение уравнения, числовое неравенство.
Статистика и теория вероятностей
-
Оперировать понятиями: столбчатые и круговые диаграммы, таблицы данных, среднее арифметическое,
-
извлекать, информацию, представленную в таблицах, на диаграммах;
-
составлять таблицы, строить диаграммы на основе данных.
В повседневной жизни и при изучении других предметов:
-
извлекать, интерпретировать и преобразовывать информацию, представленную в таблицах и на диаграммах, отражающую свойства и характеристики реальных процессов и явлений.
Текстовые задачи
-
Решать простые и сложные задачи разных типов, а также задачи повышенной трудности;
-
использовать разные краткие записи как модели текстов сложных задач для построения поисковой схемы и решения задач;
-
знать и применять оба способа поиска решения задач (от требования к условию и от условия к требованию);
-
моделировать рассуждения при поиске решения задач с помощью граф-схемы;
-
выделять этапы решения задачи и содержание каждого этапа;
-
интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;
-
анализировать всевозможные ситуации взаимного расположения двух объектов и изменение их характеристик при совместном движении (скорость, время, расстояние) при решении задач на движение двух объектов как в одном, так и в противоположных направлениях;
-
исследовать всевозможные ситуации при решении задач на движение по реке, рассматривать разные системы отсчета;
-
решать разнообразные задачи «на части»,
-
решать и обосновывать свое решение задач (выделять математическую основу) на нахождение части числа и числа по его части на основе конкретного смысла дроби;
-
осознавать и объяснять идентичность задач разных типов, связывающих три величины (на работу, на покупки, на движение); выделять эти величины и отношения между ними, применять их при решении задач, конструировать собственные задачи указанных типов.
В повседневной жизни и при изучении других предметов:
-
выделять при решении задач характеристики рассматриваемой в задаче ситуации, отличные от реальных (те, от которых абстрагировались), конструировать новые ситуации с учетом этих характеристик, в частности, при решении задач на концентрации, учитывать плотность вещества;
-
решать и конструировать задачи на основе рассмотрения реальных ситуаций, в которых не требуется точный вычислительный результат;
-
решать задачи на движение по реке, рассматривая разные системы отсчета.
Наглядная геометрия
Геометрические фигуры
-
Извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;
-
изображать изучаемые фигуры от руки и с помощью компьютерных инструментов.
Измерения и вычисления
-
выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;
-
вычислять площади прямоугольников, квадратов, объемы прямоугольных параллелепипедов, кубов.
В повседневной жизни и при изучении других предметов:
-
вычислять расстояния на местности в стандартных ситуациях, площади участков прямоугольной формы, объемы комнат;
-
выполнять простейшие построения на местности, необходимые в реальной жизни;
-
оценивать размеры реальных объектов окружающего мира.
История математики
-
Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей.
Выпускник научится в 7-9 классах (для использования в повседневной жизни и обеспечения возможности успешного продолжения образования на базовом уровне)
Элементы теории множеств и математической логики
-
Оперировать на базовом уровне3 понятиями: множество, элемент множества, подмножество, принадлежность;
-
задавать множества перечислением их элементов;
-
находить пересечение, объединение, подмножество в простейших ситуациях;
-
оперировать на базовом уровне понятиями: определение, аксиома, теорема, доказательство;
-
приводить примеры и контрпримеры для подтверждения своих высказываний.
В повседневной жизни и при изучении других предметов:
-
использовать графическое представление множеств для описания реальных процессов и явлений, при решении задач других учебных предметов.
Числа
-
Оперировать на базовом уровне понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанная дробь, рациональное число, арифметический квадратный корень;
-
использовать свойства чисел и правила действий при выполнении вычислений;
-
использовать признаки делимости на 2, 5, 3, 9, 10 при выполнении вычислений и решении несложных задач;
-
выполнять округление рациональных чисел в соответствии с правилами;
-
оценивать значение квадратного корня из положительного целого числа;
-
распознавать рациональные и иррациональные числа;
-
сравнивать числа.
В повседневной жизни и при изучении других предметов:
-
оценивать результаты вычислений при решении практических задач;
-
выполнять сравнение чисел в реальных ситуациях;
-
составлять числовые выражения при решении практических задач и задач из других учебных предметов.
Тождественные преобразования
-
Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем, степени с целым отрицательным показателем;
-
выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые;
-
использовать формулы сокращенного умножения (квадрат суммы, квадрат разности, разность квадратов) для упрощения вычислений значений выражений;
-
выполнять несложные преобразования дробно-линейных выражений и выражений с квадратными корнями.
В повседневной жизни и при изучении других предметов:
-
понимать смысл записи числа в стандартном виде;
-
оперировать на базовом уровне понятием «стандартная запись числа».
Уравнения и неравенства
-
Оперировать на базовом уровне понятиями: равенство, числовое равенство, уравнение, корень уравнения, решение уравнения, числовое неравенство, неравенство, решение неравенства;
-
проверять справедливость числовых равенств и неравенств;
-
решать линейные неравенства и несложные неравенства, сводящиеся к линейным;
-
решать системы несложных линейных уравнений, неравенств;
-
проверять, является ли данное число решением уравнения (неравенства);
-
решать квадратные уравнения по формуле корней квадратного уравнения;
-
изображать решения неравенств и их систем на числовой прямой.
В повседневной жизни и при изучении других предметов:
-
составлять и решать линейные уравнения при решении задач, возникающих в других учебных предметах.
Функции
-
Находить значение функции по заданному значению аргумента;
-
находить значение аргумента по заданному значению функции в несложных ситуациях;
-
определять положение точки по ее координатам, координаты точки по ее положению на координатной плоскости;
-
по графику находить область определения, множество значений, нули функции, промежутки знакопостоянства, промежутки возрастания и убывания, наибольшее и наименьшее значения функции;
-
строить график линейной функции;
-
проверять, является ли данный график графиком заданной функции (линейной, квадратичной, обратной пропорциональности);
-
определять приближенные значения координат точки пересечения графиков функций;
-
оперировать на базовом уровне понятиями: последовательность, арифметическая прогрессия, геометрическая прогрессия;
-
решать задачи на прогрессии, в которых ответ может быть получен непосредственным подсчетом без применения формул.
В повседневной жизни и при изучении других предметов:
-
использовать графики реальных процессов и зависимостей для определения их свойств (наибольшие и наименьшие значения, промежутки возрастания и убывания, области положительных и отрицательных значений и т.п.);
-
использовать свойства линейной функции и ее график при решении задач из других учебных предметов.
Статистика и теория вероятностей
-
Иметь представление о статистических характеристиках, вероятности случайного события, комбинаторных задачах;
-
решать простейшие комбинаторные задачи методом прямого и организованного перебора;
-
представлять данные в виде таблиц, диаграмм, графиков;
-
читать информацию, представленную в виде таблицы, диаграммы, графика;
-
определять основные статистические характеристики числовых наборов;
-
оценивать вероятность события в простейших случаях;
-
иметь представление о роли закона больших чисел в массовых явлениях.
В повседневной жизни и при изучении других предметов:
-
оценивать количество возможных вариантов методом перебора;
-
иметь представление о роли практически достоверных и маловероятных событий;
-
сравнивать основные статистические характеристики, полученные в процессе решения прикладной задачи, изучения реального явления;
-
оценивать вероятность реальных событий и явлений в несложных ситуациях.
Текстовые задачи
-
Решать несложные сюжетные задачи разных типов на все арифметические действия;
-
строить модель условия задачи (в виде таблицы, схемы, рисунка или уравнения), в которой даны значения двух из трех взаимосвязанных величин, с целью поиска решения задачи;
-
осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию;
-
составлять план решения задачи;
-
выделять этапы решения задачи;
-
интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;
-
знать различие скоростей объекта в стоячей воде, против течения и по течению реки;
-
решать задачи на нахождение части числа и числа по его части;
-
решать задачи разных типов (на работу, на покупки, на движение), связывающих три величины, выделять эти величины и отношения между ними;
-
находить процент от числа, число по проценту от него, находить процентное снижение или процентное повышение величины;
-
решать несложные логические задачи методом рассуждений.
В повседневной жизни и при изучении других предметов:
-
выдвигать гипотезы о возможных предельных значениях искомых в задаче величин (делать прикидку).
Геометрические фигуры
-
Оперировать на базовом уровне понятиями геометрических фигур;
-
извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;
-
применять для решения задач геометрические факты, если условия их применения заданы в явной форме;
-
решать задачи на нахождение геометрических величин по образцам или алгоритмам.
В повседневной жизни и при изучении других предметов:
-
использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания.
Отношения
-
Оперировать на базовом уровне понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция.
В повседневной жизни и при изучении других предметов:
-
использовать отношения для решения простейших задач, возникающих в реальной жизни.
Измерения и вычисления
-
Выполнять измерение длин, расстояний, величин углов, с помощью инструментов для измерений длин и углов;
-
применять формулы периметра, площади и объема, площади поверхности отдельных многогранников при вычислениях, когда все данные имеются в условии;
-
применять теорему Пифагора, базовые тригонометрические соотношения для вычисления длин, расстояний, площадей в простейших случаях.
В повседневной жизни и при изучении других предметов:
-
вычислять расстояния на местности в стандартных ситуациях, площади в простейших случаях, применять формулы в простейших ситуациях в повседневной жизни.
Геометрические построения
-
Изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.
В повседневной жизни и при изучении других предметов:
-
выполнять простейшие построения на местности, необходимые в реальной жизни.
Геометрические преобразования
-
Строить фигуру, симметричную данной фигуре относительно оси и точки.
В повседневной жизни и при изучении других предметов:
-
распознавать движение объектов в окружающем мире;
-
распознавать симметричные фигуры в окружающем мире.
Векторы и координаты на плоскости
-
Оперировать на базовом уровне понятиями вектор, сумма векторов, произведение вектора на число, координаты на плоскости;
-
определять приближенно координаты точки по ее изображению на координатной плоскости.
В повседневной жизни и при изучении других предметов:
-
использовать векторы для решения простейших задач на определение скорости относительного движения.
История математики
-
Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;
-
знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;
-
понимать роль математики в развитии России.
Методы математики
-
Выбирать подходящий изученный метод для решения изученных типов математических задач;
-
Приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.
Выпускник получит возможность научиться в 7-9 классах для обеспечения возможности успешного продолжения образования на базовом и углубленном уровнях
Элементы теории множеств и математической логики
-
Оперировать4 понятиями: определение, теорема, аксиома, множество, характеристики множества, элемент множества, пустое, конечное и бесконечное множество, подмножество, принадлежность, включение, равенство множеств;
-
изображать множества и отношение множеств с помощью кругов Эйлера;
-
определять принадлежность элемента множеству, объединению и пересечению множеств;
-
задавать множество с помощью перечисления элементов, словесного описания;
-
оперировать понятиями: высказывание, истинность и ложность высказывания, отрицание высказываний, операции над высказываниями: и, или, не, условные высказывания (импликации);
-
строить высказывания, отрицания высказываний.
В повседневной жизни и при изучении других предметов:
-
строить цепочки умозаключений на основе использования правил логики;
-
использовать множества, операции с множествами, их графическое представление для описания реальных процессов и явлений.
Числа
-
Оперировать понятиями: множество натуральных чисел, множество целых чисел, множество рациональных чисел, иррациональное число, квадратный корень, множество действительных чисел, геометрическая интерпретация натуральных, целых, рациональных, действительных чисел;
-
понимать и объяснять смысл позиционной записи натурального числа;
-
выполнять вычисления, в том числе с использованием приемов рациональных вычислений;
-
выполнять округление рациональных чисел с заданной точностью;
-
сравнивать рациональные и иррациональные числа;
-
представлять рациональное число в виде десятичной дроби
-
упорядочивать числа, записанные в виде обыкновенной и десятичной дроби;
-
находить НОД и НОК чисел и использовать их при решении задач.
В повседневной жизни и при изучении других предметов:
-
применять правила приближенных вычислений при решении практических задач и решении задач других учебных предметов;
-
выполнять сравнение результатов вычислений при решении практических задач, в том числе приближенных вычислений;
-
составлять и оценивать числовые выражения при решении практических задач и задач из других учебных предметов;
-
записывать и округлять числовые значения реальных величин с использованием разных систем измерения.
Тождественные преобразования
-
Оперировать понятиями степени с натуральным показателем, степени с целым отрицательным показателем;
-
выполнять преобразования целых выражений: действия с одночленами (сложение, вычитание, умножение), действия с многочленами (сложение, вычитание, умножение);
-
выполнять разложение многочленов на множители одним из способов: вынесение за скобку, группировка, использование формул сокращенного умножения;
-
выделять квадрат суммы и разности одночленов;
-
раскладывать на множители квадратный трехчлен;
-
выполнять преобразования выражений, содержащих степени с целыми отрицательными показателями, переходить от записи в виде степени с целым отрицательным показателем к записи в виде дроби;
-
выполнять преобразования дробно-рациональных выражений: сокращение дробей, приведение алгебраических дробей к общему знаменателю, сложение, умножение, деление алгебраических дробей, возведение алгебраической дроби в натуральную и целую отрицательную степень;
-
выполнять преобразования выражений, содержащих квадратные корни;
-
выделять квадрат суммы или разности двучлена в выражениях, содержащих квадратные корни;
-
выполнять преобразования выражений, содержащих модуль.
В повседневной жизни и при изучении других предметов:
-
выполнять преобразования и действия с числами, записанными в стандартном виде;
-
выполнять преобразования алгебраических выражений при решении задач других учебных предметов.
Уравнения и неравенства
-
Оперировать понятиями: уравнение, неравенство, корень уравнения, решение неравенства, равносильные уравнения, область определения уравнения (неравенства, системы уравнений или неравенств);
-
решать линейные уравнения и уравнения, сводимые к линейным с помощью тождественных преобразований;
-
решать квадратные уравнения и уравнения, сводимые к квадратным с помощью тождественных преобразований;
-
решать дробно-линейные уравнения;
-
решать простейшие иррациональные уравнения вида
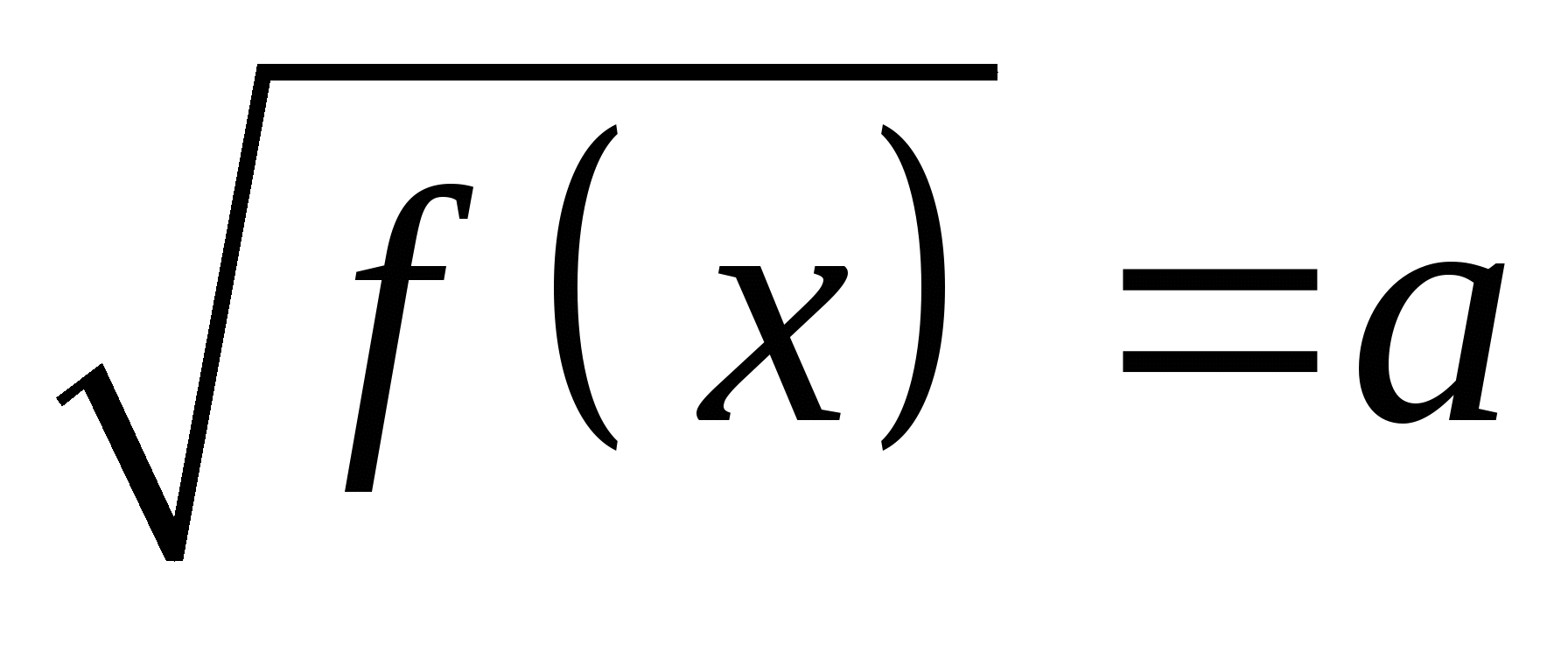 ,
,
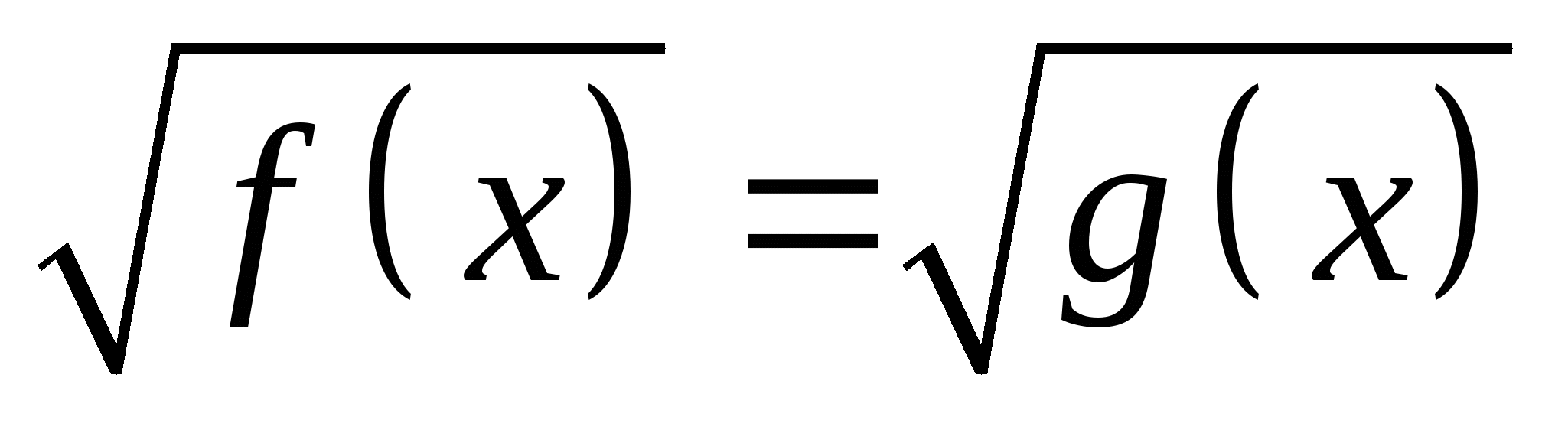 ;
;
-
решать уравнения вида
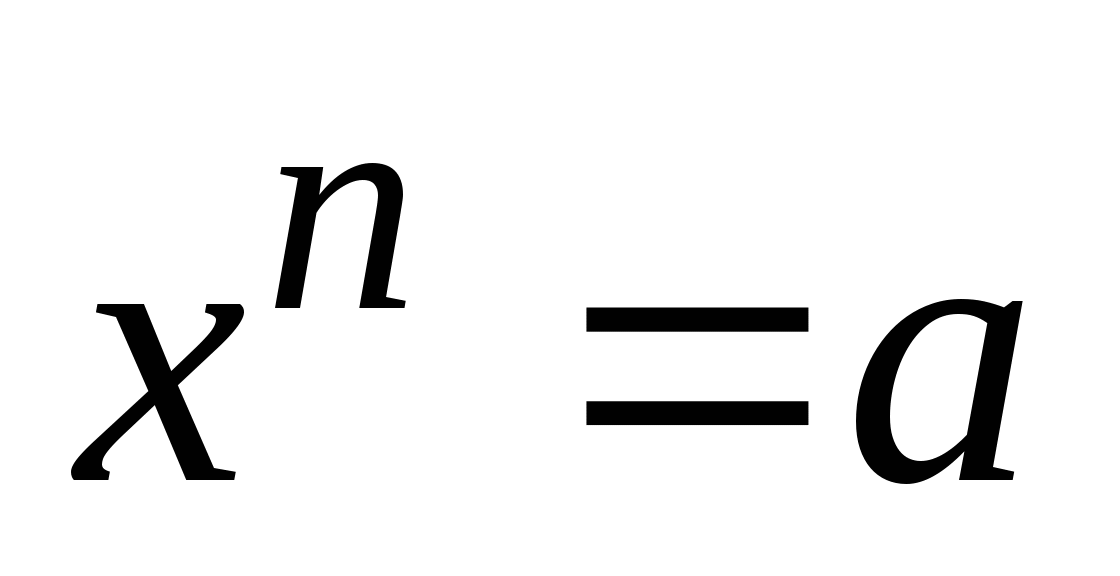 ;
;
-
решать уравнения способом разложения на множители и замены переменной;
-
использовать метод интервалов для решения целых и дробно-рациональных неравенств;
-
решать линейные уравнения и неравенства с параметрами;
-
решать несложные квадратные уравнения с параметром;
-
решать несложные системы линейных уравнений с параметрами;
-
решать несложные уравнения в целых числах.
В повседневной жизни и при изучении других предметов:
-
составлять и решать линейные и квадратные уравнения, уравнения, к ним сводящиеся, системы линейных уравнений, неравенств при решении задач других учебных предметов;
-
выполнять оценку правдоподобия результатов, получаемых при решении линейных и квадратных уравнений и систем линейных уравнений и неравенств при решении задач других учебных предметов;
-
выбирать соответствующие уравнения, неравенства или их системы для составления математической модели заданной реальной ситуации или прикладной задачи;
-
уметь интерпретировать полученный при решении уравнения, неравенства или системы результат в контексте заданной реальной ситуации или прикладной задачи.
Функции
-
Оперировать понятиями: функциональная зависимость, функция, график функции, способы задания функции, аргумент и значение функции, область определения и множество значений функции, нули функции, промежутки знакопостоянства, монотонность функции, четность/нечетность функции;
-
строить графики линейной, квадратичной функций, обратной пропорциональности, функции вида:
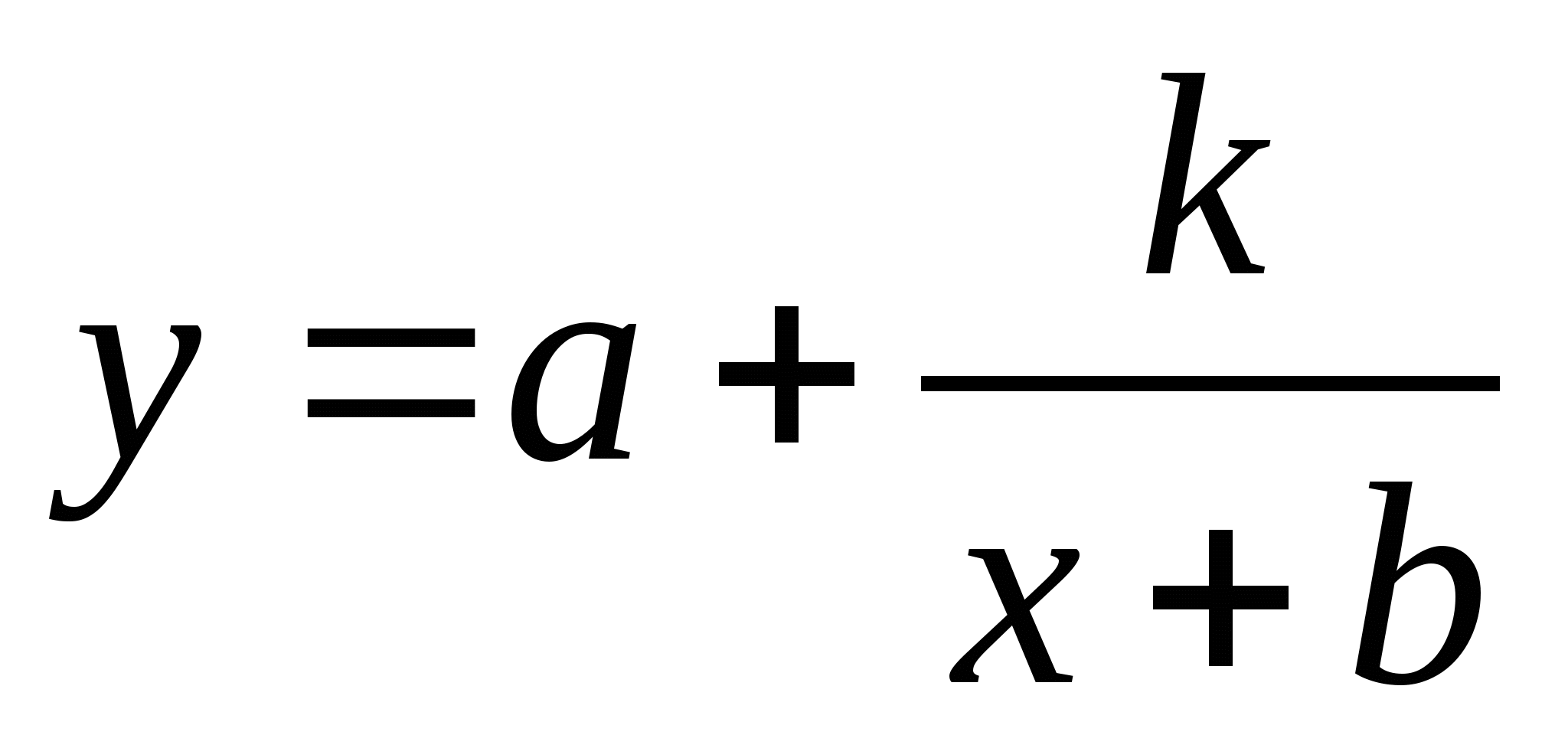 ,
,
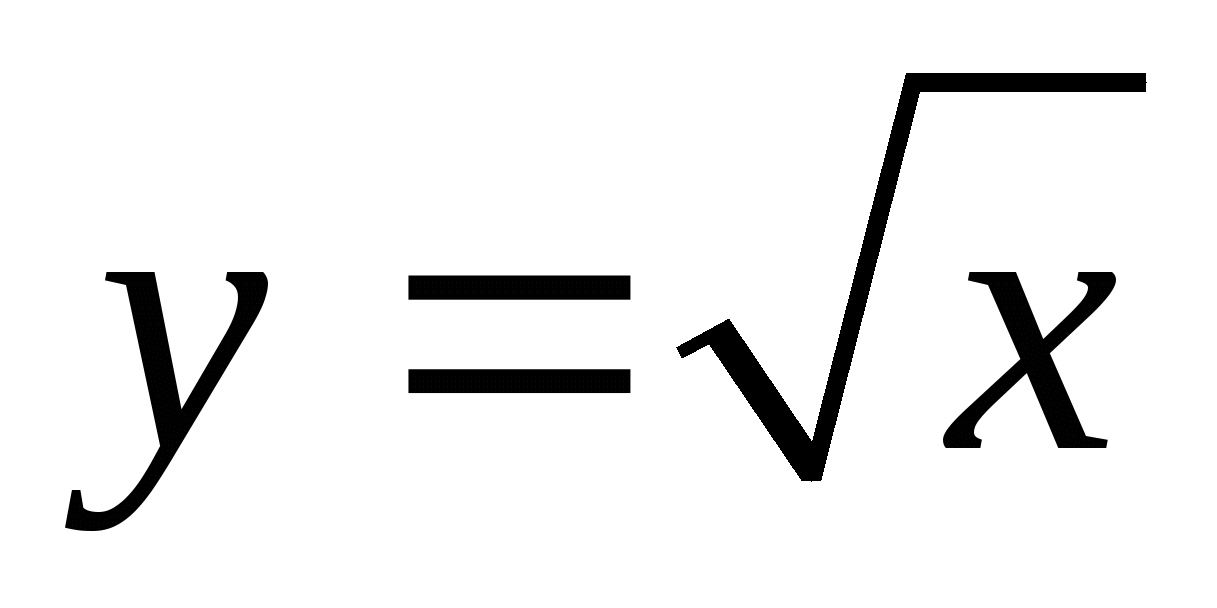 ,
,
 ,
,
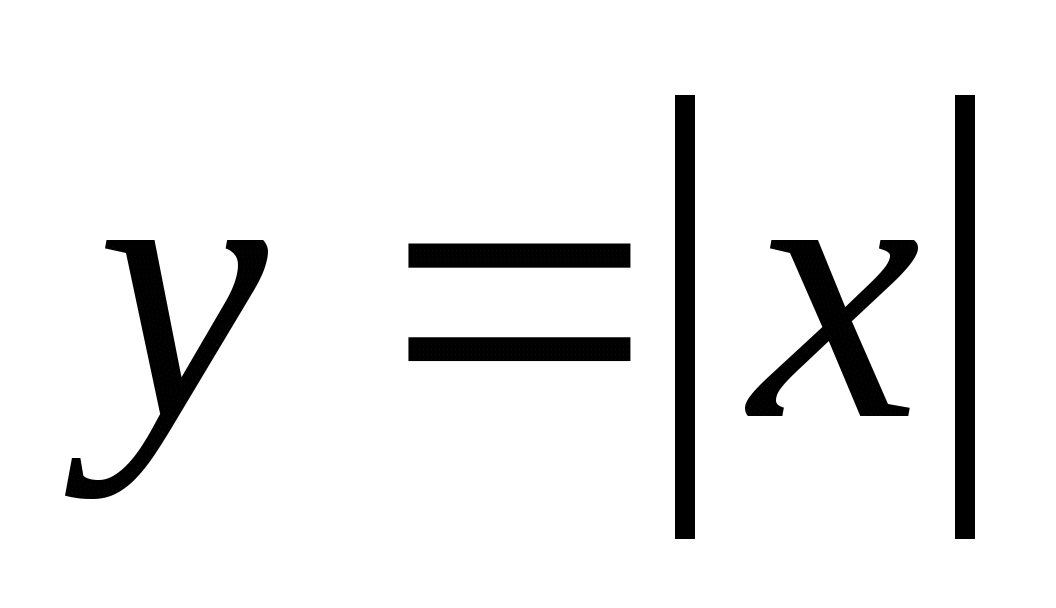 ;
;
-
на примере квадратичной функции, использовать преобразования графика функции y=f(x) для построения графиков функций
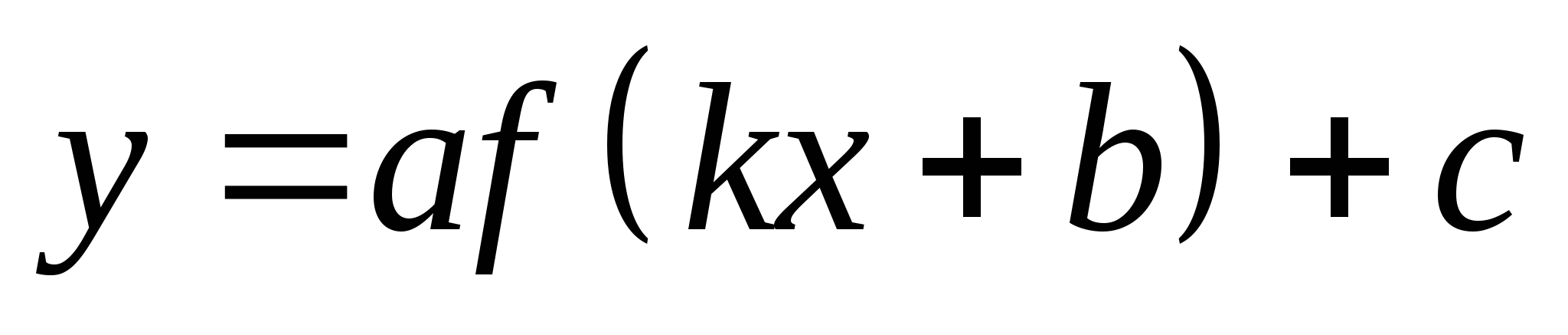 ;
;
-
составлять уравнения прямой по заданным условиям: проходящей через две точки с заданными координатами, проходящей через данную точку и параллельной данной прямой;
-
исследовать функцию по ее графику;
-
находить множество значений, нули, промежутки знакопостоянства, монотонности квадратичной функции;
-
оперировать понятиями: последовательность, арифметическая прогрессия, геометрическая прогрессия;
-
решать задачи на арифметическую и геометрическую прогрессию.
В повседневной жизни и при изучении других предметов:
-
иллюстрировать с помощью графика реальную зависимость или процесс по их характеристикам;
-
использовать свойства и график квадратичной функции при решении задач из других учебных предметов.
Текстовые задачи
-
Решать простые и сложные задачи разных типов, а также задачи повышенной трудности;
-
использовать разные краткие записи как модели текстов сложных задач для построения поисковой схемы и решения задач;
-
различать модель текста и модель решения задачи, конструировать к одной модели решения несложной задачи разные модели текста задачи;
-
знать и применять оба способа поиска решения задач (от требования к условию и от условия к требованию);
-
моделировать рассуждения при поиске решения задач с помощью граф-схемы;
-
выделять этапы решения задачи и содержание каждого этапа;
-
уметь выбирать оптимальный метод решения задачи и осознавать выбор метода, рассматривать различные методы, находить разные решения задачи, если возможно;
-
анализировать затруднения при решении задач;
-
выполнять различные преобразования предложенной задачи, конструировать новые задачи из данной, в том числе обратные;
-
интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;
-
анализировать всевозможные ситуации взаимного расположения двух объектов и изменение их характеристик при совместном движении (скорость, время, расстояние) при решении задач на движение двух объектов как в одном, так и в противоположных направлениях;
-
исследовать всевозможные ситуации при решении задач на движение по реке, рассматривать разные системы отсчета;
-
решать разнообразные задачи «на части»,
-
решать и обосновывать свое решение задач (выделять математическую основу) на нахождение части числа и числа по его части на основе конкретного смысла дроби;
-
осознавать и объяснять идентичность задач разных типов, связывающих три величины (на работу, на покупки, на движение), выделять эти величины и отношения между ними, применять их при решении задач, конструировать собственные задач указанных типов;
-
владеть основными методами решения задач на смеси, сплавы, концентрации;
-
решать задачи на проценты, в том числе, сложные проценты с обоснованием, используя разные способы;
-
решать логические задачи разными способами, в том числе, с двумя блоками и с тремя блоками данных с помощью таблиц;
-
решать задачи по комбинаторике и теории вероятностей на основе использования изученных методов и обосновывать решение;
-
решать несложные задачи по математической статистике;
-
овладеть основными методами решения сюжетных задач: арифметический, алгебраический, перебор вариантов, геометрический, графический, применять их в новых по сравнению с изученными ситуациях.
В повседневной жизни и при изучении других предметов:
-
выделять при решении задач характеристики рассматриваемой в задаче ситуации, отличные от реальных (те, от которых абстрагировались), конструировать новые ситуации с учетом этих характеристик, в частности, при решении задач на концентрации, учитывать плотность вещества;
-
решать и конструировать задачи на основе рассмотрения реальных ситуаций, в которых не требуется точный вычислительный результат;
-
решать задачи на движение по реке, рассматривая разные системы отсчета.
Статистика и теория вероятностей
-
Оперировать понятиями: столбчатые и круговые диаграммы, таблицы данных, среднее арифметическое, медиана, наибольшее и наименьшее значения выборки, размах выборки, дисперсия и стандартное отклонение, случайная изменчивость;
-
извлекать информацию, представленную в таблицах, на диаграммах, графиках;
-
составлять таблицы, строить диаграммы и графики на основе данных;
-
оперировать понятиями: факториал числа, перестановки и сочетания, треугольник Паскаля;
-
применять правило произведения при решении комбинаторных задач;
-
оперировать понятиями: случайный опыт, случайный выбор, испытание, элементарное случайное событие (исход), классическое определение вероятности случайного события, операции над случайными событиями;
-
представлять информацию с помощью кругов Эйлера;
-
решать задачи на вычисление вероятности с подсчетом количества вариантов с помощью комбинаторики.
В повседневной жизни и при изучении других предметов:
-
извлекать, интерпретировать и преобразовывать информацию, представленную в таблицах, на диаграммах, графиках, отражающую свойства и характеристики реальных процессов и явлений;
-
определять статистические характеристики выборок по таблицам, диаграммам, графикам, выполнять сравнение в зависимости от цели решения задачи;
-
оценивать вероятность реальных событий и явлений.
Геометрические фигуры
-
Оперировать понятиями геометрических фигур;
-
извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;
-
применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения;
-
формулировать в простейших случаях свойства и признаки фигур;
-
доказывать геометрические утверждения;
-
владеть стандартной классификацией плоских фигур (треугольников и четырехугольников).
В повседневной жизни и при изучении других предметов:
-
использовать свойства геометрических фигур для решения задач практического характера и задач из смежных дисциплин.
Отношения
-
Оперировать понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция, подобие фигур, подобные фигуры, подобные треугольники;
-
применять теорему Фалеса и теорему о пропорциональных отрезках при решении задач;
-
характеризовать взаимное расположение прямой и окружности, двух окружностей.
В повседневной жизни и при изучении других предметов:
-
использовать отношения для решения задач, возникающих в реальной жизни.
Измерения и вычисления
-
Оперировать представлениями о длине, площади, объеме как величинами. Применять теорему Пифагора, формулы площади, объема при решении многошаговых задач, в которых не все данные представлены явно, а требуют вычислений, оперировать более широким количеством формул длины, площади, объема, вычислять характеристики комбинаций фигур (окружностей и многоугольников) вычислять расстояния между фигурами, применять тригонометрические формулы для вычислений в более сложных случаях, проводить вычисления на основе равновеликости и равносоставленности;
-
проводить простые вычисления на объемных телах;
-
формулировать задачи на вычисление длин, площадей и объемов и решать их.
В повседневной жизни и при изучении других предметов:
-
проводить вычисления на местности;
-
применять формулы при вычислениях в смежных учебных предметах, в окружающей действительности.
Геометрические построения
-
Изображать геометрические фигуры по текстовому и символьному описанию;
-
свободно оперировать чертежными инструментами в несложных случаях,
-
выполнять построения треугольников, применять отдельные методы построений циркулем и линейкой и проводить простейшие исследования числа решений;
-
изображать типовые плоские фигуры и объемные тела с помощью простейших компьютерных инструментов.
В повседневной жизни и при изучении других предметов:
-
выполнять простейшие построения на местности, необходимые в реальной жизни;
-
оценивать размеры реальных объектов окружающего мира.
Преобразования
-
Оперировать понятием движения и преобразования подобия, владеть приемами построения фигур с использованием движений и преобразований подобия, применять полученные знания и опыт построений в смежных предметах и в реальных ситуациях окружающего мира;
-
строить фигуру, подобную данной, пользоваться свойствами подобия для обоснования свойств фигур;
-
применять свойства движений для проведения простейших обоснований свойств фигур.
В повседневной жизни и при изучении других предметов:
-
применять свойства движений и применять подобие для построений и вычислений.
Векторы и координаты на плоскости
-
Оперировать понятиями вектор, сумма, разность векторов, произведение вектора на число, угол между векторами, скалярное произведение векторов, координаты на плоскости, координаты вектора;
-
выполнять действия над векторами (сложение, вычитание, умножение на число), вычислять скалярное произведение, определять в простейших случаях угол между векторами, выполнять разложение вектора на составляющие, применять полученные знания в физике, пользоваться формулой вычисления расстояния между точками по известным координатам, использовать уравнения фигур для решения задач;
-
применять векторы и координаты для решения геометрических задач на вычисление длин, углов.
В повседневной жизни и при изучении других предметов:
-
использовать понятия векторов и координат для решения задач по физике, географии и другим учебным предметам.
История математики
-
Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;
-
понимать роль математики в развитии России.
Методы математики
-
Используя изученные методы, проводить доказательство, выполнять опровержение;
-
выбирать изученные методы и их комбинации для решения математических задач;
-
использовать математические знания для описания закономерностей в окружающей действительности и произведениях искусства;
-
применять простейшие программные средства и электронно-коммуникационные системы при решении математических задач.
Выпускник получит возможность научиться в 7-9 классах для успешного продолжения образования на углубленном уровне
Элементы теории множеств и математической логики
-
Свободно оперировать5 понятиями: множество, характеристики множества, элемент множества, пустое, конечное и бесконечное множество, подмножество, принадлежность, включение, равенство множеств, способы задание множества;
-
задавать множества разными способами;
-
проверять выполнение характеристического свойства множества;
-
свободно оперировать понятиями: высказывание, истинность и ложность высказывания, сложные и простые высказывания, отрицание высказываний; истинность и ложность утверждения и его отрицания, операции над высказываниями: и, или, не; условные высказывания (импликации);
-
строить высказывания с использованием законов алгебры высказываний.
В повседневной жизни и при изучении других предметов:
-
строить рассуждения на основе использования правил логики;
-
использовать множества, операции с множествами, их графическое представление для описания реальных процессов и явлений, при решении задач других учебных предметов.
Числа
-
Свободно оперировать понятиями: натуральное число, множество натуральных чисел, целое число, множество целых чисел, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число, множество рациональных чисел, иррациональное число, корень степени n, действительное число, множество действительных чисел, геометрическая интерпретация натуральных, целых, рациональных, действительных чисел;
-
понимать и объяснять разницу между позиционной и непозиционной системами записи чисел;
-
переводить числа из одной системы записи (системы счисления) в другую;
-
доказывать и использовать признаки делимости на 2, 4, 8, 5, 3, 6, 9, 10, 11 суммы и произведения чисел при выполнении вычислений и решении задач;
-
выполнять округление рациональных и иррациональных чисел с заданной точностью;
-
сравнивать действительные числа разными способами;
-
упорядочивать числа, записанные в виде обыкновенной и десятичной дроби, числа, записанные с использованием арифметического квадратного корня, корней степени больше 2;
-
находить НОД и НОК чисел разными способами и использовать их при решении задач;
-
выполнять вычисления и преобразования выражений, содержащих действительные числа, в том числе корни натуральных степеней.
В повседневной жизни и при изучении других предметов:
-
выполнять и объяснять результаты сравнения результатов вычислений при решении практических задач, в том числе приближенных вычислений, используя разные способы сравнений;
-
записывать, сравнивать, округлять числовые данные реальных величин с использованием разных систем измерения;
-
составлять и оценивать разными способами числовые выражения при решении практических задач и задач из других учебных предметов.
Тождественные преобразования
-
Свободно оперировать понятиями степени с целым и дробным показателем;
-
выполнять доказательство свойств степени с целыми и дробными показателями;
-
оперировать понятиями «одночлен», «многочлен», «многочлен с одной переменной», «многочлен с несколькими переменными», коэффициенты многочлена, «стандартная запись многочлена», степень одночлена и многочлена;
-
свободно владеть приемами преобразования целых и дробно-рациональных выражений;
-
выполнять разложение многочленов на множители разными способами, с использованием комбинаций различных приемов;
-
использовать теорему Виета и теорему, обратную теореме Виета, для поиска корней квадратного трехчлена и для решения задач, в том числе задач с параметрами на основе квадратного трехчлена;
-
выполнять деление многочлена на многочлен с остатком;
-
доказывать свойства квадратных корней и корней степени n;
-
выполнять преобразования выражений, содержащих квадратные корни, корни степени n;
-
свободно оперировать понятиями «тождество», «тождество на множестве», «тождественное преобразование»;
-
выполнять различные преобразования выражений, содержащих модули.
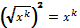
В повседневной жизни и при изучении других предметов:
-
выполнять преобразования и действия с буквенными выражениями, числовые коэффициенты которых записаны в стандартном виде;
-
выполнять преобразования рациональных выражений при решении задач других учебных предметов;
-
выполнять проверку правдоподобия физических и химических формул на основе сравнения размерностей и валентностей.
Уравнения и неравенства
-
Свободно оперировать понятиями: уравнение, неравенство, равносильные уравнения и неравенства, уравнение, являющееся следствием другого уравнения, уравнения, равносильные на множестве, равносильные преобразования уравнений;
-
решать разные виды уравнений и неравенств и их систем, в том числе некоторые уравнения 3 и 4 степеней, дробно-рациональные и иррациональные;
-
знать теорему Виета для уравнений степени выше второй;
-
понимать смысл теорем о равносильных и неравносильных преобразованиях уравнений и уметь их доказывать;
-
владеть разными методами решения уравнений, неравенств и их систем, уметь выбирать метод решения и обосновывать свой выбор;
-
использовать метод интервалов для решения неравенств, в том числе дробно-рациональных и включающих в себя иррациональные выражения;
-
решать алгебраические уравнения и неравенства и их системы с параметрами алгебраическим и графическим методами;
-
владеть разными методами доказательства неравенств;
-
решать уравнения в целых числах;
-
изображать множества на плоскости, задаваемые уравнениями, неравенствами и их системами.
В повседневной жизни и при изучении других предметов:
-
составлять и решать уравнения, неравенства, их системы при решении задач других учебных предметов;
-
выполнять оценку правдоподобия результатов, получаемых при решении различных уравнений, неравенств и их систем при решении задач других учебных предметов;
-
составлять и решать уравнения и неравенства с параметрами при решении задач других учебных предметов;
-
составлять уравнение, неравенство или их систему, описывающие реальную ситуацию или прикладную задачу, интерпретировать полученные результаты.
Функции
-
Свободно оперировать понятиями: зависимость, функциональная зависимость, зависимая и независимая переменные, функция, способы задания функции, аргумент и значение функции, область определения и множество значения функции, нули функции, промежутки знакопостоянства, монотонность функции, наибольшее и наименьшее значения, четность/нечетность функции, периодичность функции, график функции, вертикальная, горизонтальная, наклонная асимптоты; график зависимости, не являющейся функцией,
-
строить графики функций: линейной, квадратичной, дробно-линейной, степенной при разных значениях показателя степени,
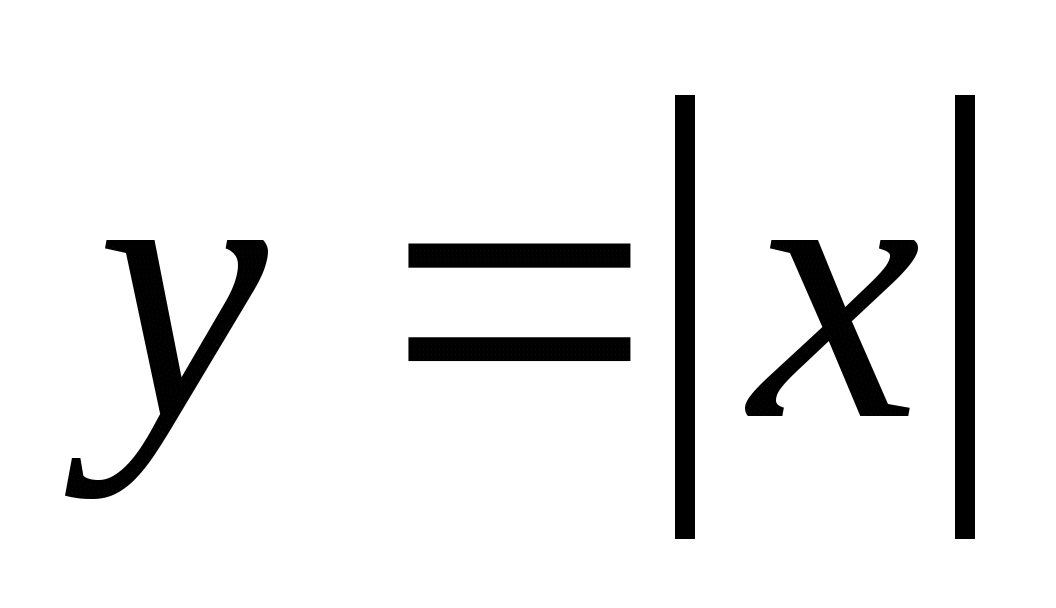 ;
;
-
использовать преобразования графика функции
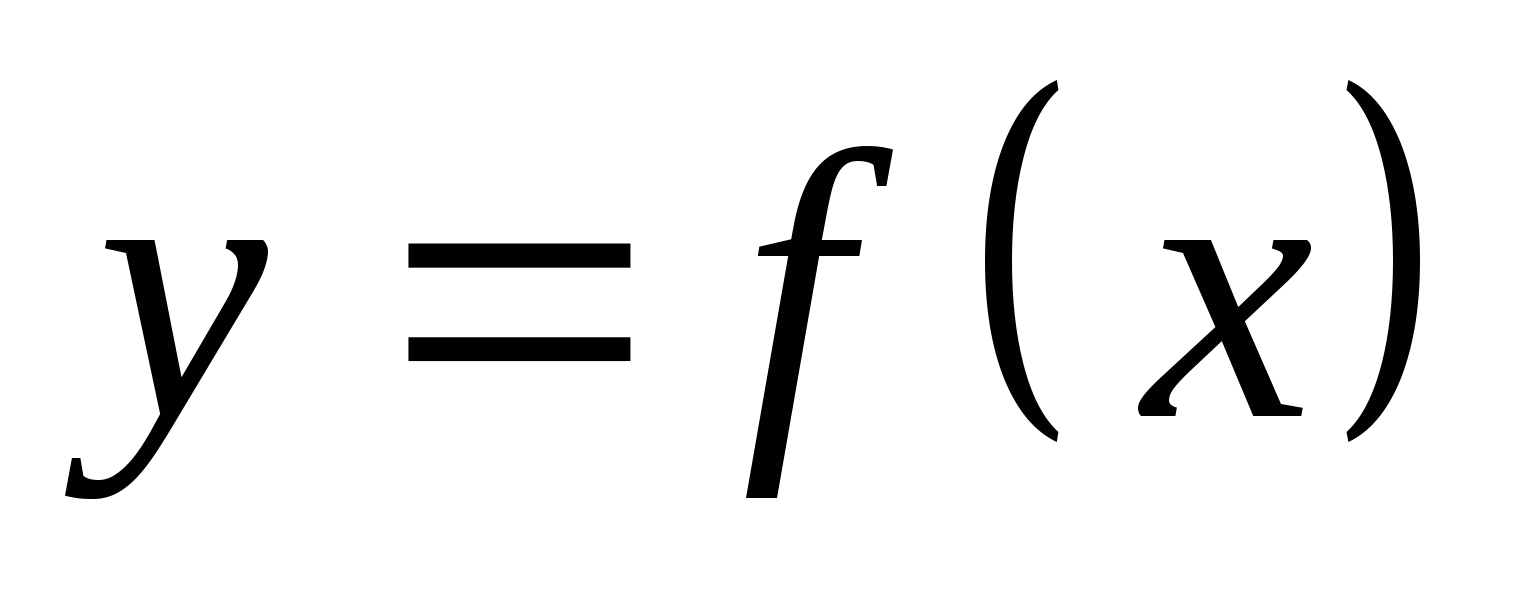 для
построения графиков функций
для
построения графиков функций 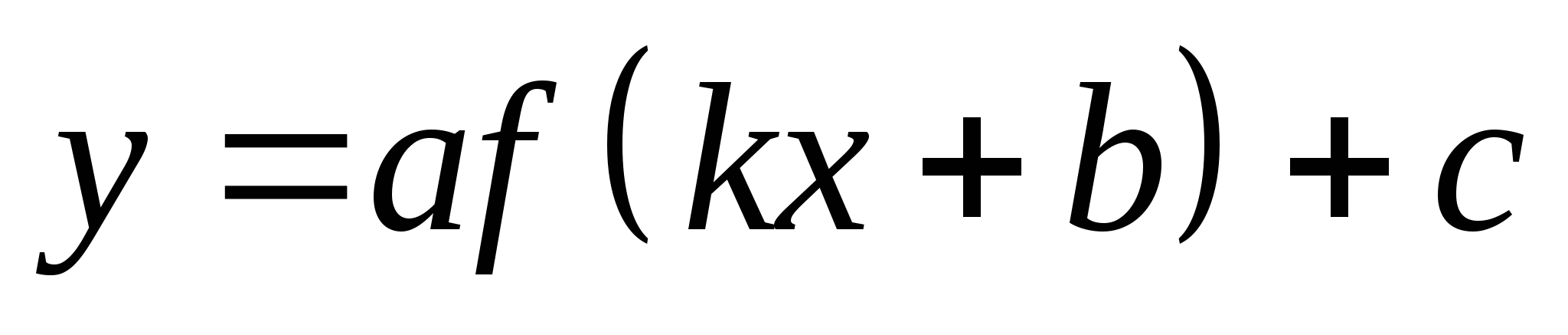 ;
;
-
анализировать свойства функций и вид графика в зависимости от параметров;
-
свободно оперировать понятиями: последовательность, ограниченная последовательность, монотонно возрастающая (убывающая) последовательность, предел последовательности, арифметическая прогрессия, геометрическая прогрессия, характеристическое свойство арифметической (геометрической) прогрессии;
-
использовать метод математической индукции для вывода формул, доказательства равенств и неравенств, решения задач на делимость;
-
исследовать последовательности, заданные рекуррентно;
-
решать комбинированные задачи на арифметическую и геометрическую прогрессии.
В повседневной жизни и при изучении других предметов:
-
конструировать и исследовать функции, соответствующие реальным процессам и явлениям, интерпретировать полученные результаты в соответствии со спецификой исследуемого процесса или явления;
-
использовать графики зависимостей для исследования реальных процессов и явлений;
-
конструировать и исследовать функции при решении задач других учебных предметов, интерпретировать полученные результаты в соответствии со спецификой учебного предмета.
Статистика и теория вероятностей
-
Свободно оперировать понятиями: столбчатые и круговые диаграммы, таблицы данных, среднее арифметическое, медиана, наибольшее и наименьшее значения выборки, размах выборки, дисперсия и стандартное отклонение, случайная изменчивость;
-
выбирать наиболее удобный способ представления информации, адекватный ее свойствам и целям анализа;
-
вычислять числовые характеристики выборки;
-
свободно оперировать понятиями: факториал числа, перестановки, сочетания и размещения, треугольник Паскаля;
-
свободно оперировать понятиями: случайный опыт, случайный выбор, испытание, элементарное случайное событие (исход), классическое определение вероятности случайного события, операции над случайными событиями, основные комбинаторные формулы;
-
свободно оперировать понятиями: случайный опыт, случайный выбор, испытание, элементарное случайное событие (исход), классическое определение вероятности случайного события, операции над случайными событиями, основные комбинаторные формулы;
-
знать примеры случайных величин, и вычислять их статистические характеристики;
-
использовать формулы комбинаторики при решении комбинаторных задач;
-
решать задачи на вычисление вероятности в том числе с использованием формул.
В повседневной жизни и при изучении других предметов:
-
представлять информацию о реальных процессах и явлениях способом, адекватным ее свойствам и цели исследования;
-
анализировать и сравнивать статистические характеристики выборок, полученных в процессе решения прикладной задачи, изучения реального явления, решения задачи из других учебных предметов;
-
оценивать вероятность реальных событий и явлений в различных ситуациях.
Текстовые задачи
-
Решать простые и сложные задачи, а также задачи повышенной трудности и выделять их математическую основу;
-
распознавать разные виды и типы задач;
-
использовать разные краткие записи как модели текстов сложных задач и задач повышенной сложности для построения поисковой схемы и решения задач, выбирать оптимальную для рассматриваемой в задаче ситуации модель текста задачи;
-
различать модель текста и модель решения задачи, конструировать к одной модели решения сложных задач разные модели текста задачи;
-
знать и применять три способа поиска решения задач (от требования к условию и от условия к требованию, комбинированный);
-
моделировать рассуждения при поиске решения задач с помощью граф-схемы;
-
выделять этапы решения задачи и содержание каждого этапа;
-
уметь выбирать оптимальный метод решения задачи и осознавать выбор метода, рассматривать различные методы, находить разные решения задачи, если возможно;
-
анализировать затруднения при решении задач;
-
выполнять различные преобразования предложенной задачи, конструировать новые задачи из данной, в том числе обратные;
-
интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;
-
изменять условие задач (количественные или качественные данные), исследовать измененное преобразованное;
-
анализировать всевозможные ситуации взаимного расположения двух объектов и изменение их характеристик при совместном движении (скорость, время, расстояние) при решении задач на движение двух объектов как в одном, так и в противоположных направлениях, конструировать новые ситуации на основе изменения условий задачи при движении по реке;
-
исследовать всевозможные ситуации при решении задач на движение по реке, рассматривать разные системы отсчета;
-
решать разнообразные задачи «на части»;
-
решать и обосновывать свое решение задач (выделять математическую основу) на нахождение части числа и числа по его части на основе конкретного смысла дроби;
-
объяснять идентичность задач разных типов, связывающих три величины (на работу, на покупки, на движение), выделять эти величины и отношения между ними, применять их при решении задач, конструировать собственные задач указанных типов;
-
владеть основными методами решения задач на смеси, сплавы, концентрации, использовать их в новых ситуациях по отношению к изученным в процессе обучения;
-
решать задачи на проценты, в том числе, сложные проценты с обоснованием, используя разные способы;
-
решать логические задачи разными способами, в том числе, с двумя блоками и с тремя блоками данных с помощью таблиц;
-
решать задачи по комбинаторике и теории вероятностей на основе использования изученных методов и обосновывать решение;
-
решать несложные задачи по математической статистике;
-
овладеть основными методами решения сюжетных задач: арифметический, алгебраический, перебор вариантов, геометрический, графический, применять их в новых по сравнению с изученными ситуациях.
В повседневной жизни и при изучении других предметов:
-
конструировать новые для данной задачи задачные ситуации с учетом реальных характеристик, в частности, при решении задач на концентрации, учитывать плотность вещества; решать и конструировать задачи на основе рассмотрения реальных ситуаций, в которых не требуется точный вычислительный результат;
-
решать задачи на движение по реке, рассматривая разные системы отсчета;
-
конструировать задачные ситуации, приближенные к реальной действительности.
Геометрические фигуры
-
Свободно оперировать геометрическими понятиями при решении задач и проведении математических рассуждений;
-
самостоятельно формулировать определения геометрических фигур, выдвигать гипотезы о новых свойствах и признаках геометрических фигур и обосновывать или опровергать их, обобщать или конкретизировать результаты на новые классы фигур, проводить в несложных случаях классификацию фигур по различным основаниям;
-
исследовать чертежи, включая комбинации фигур, извлекать, интерпретировать и преобразовывать информацию, представленную на чертежах;
-
решать задачи геометрического содержания, в том числе в ситуациях, когда алгоритм решения не следует явно из условия, выполнять необходимые для решения задачи дополнительные построения, исследовать возможность применения теорем и формул для решения задач;
-
формулировать и доказывать геометрические утверждения.
В повседневной жизни и при изучении других предметов:
-
составлять с использованием свойств геометрических фигур математические модели для решения задач практического характера и задач из смежных дисциплин, исследовать полученные модели и интерпретировать результат.
Отношения
-
Владеть понятием отношения как метапредметным;
-
свободно оперировать понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция, подобие фигур, подобные фигуры, подобные треугольники;
-
использовать свойства подобия и равенства фигур при решении задач.
В повседневной жизни и при изучении других предметов:
-
использовать отношения для построения и исследования математических моделей объектов реальной жизни.
Измерения и вычисления
-
Свободно оперировать понятиями длина, площадь, объем, величина угла как величинами, использовать равновеликость и равносоставленность при решении задач на вычисление, самостоятельно получать и использовать формулы для вычислений площадей и объемов фигур, свободно оперировать широким набором формул на вычисление при решении сложных задач, в том числе и задач на вычисление в комбинациях окружности и треугольника, окружности и четырехугольника, а также с применением тригонометрии;
-
самостоятельно формулировать гипотезы и проверять их достоверность.
В повседневной жизни и при изучении других предметов:
-
свободно оперировать формулами при решении задач в других учебных предметах и при проведении необходимых вычислений в реальной жизни.
Геометрические построения
-
Оперировать понятием набора элементов, определяющих геометрическую фигуру,
-
владеть набором методов построений циркулем и линейкой;
-
проводить анализ и реализовывать этапы решения задач на построение.
В повседневной жизни и при изучении других предметов:
-
выполнять построения на местности;
-
оценивать размеры реальных объектов окружающего мира.
Преобразования
-
Оперировать движениями и преобразованиями как метапредметными понятиями;
-
оперировать понятием движения и преобразования подобия для обоснований, свободно владеть приемами построения фигур с помощью движений и преобразования подобия, а также комбинациями движений, движений и преобразований;
-
использовать свойства движений и преобразований для проведения обоснования и доказательства утверждений в геометрии и других учебных предметах;
-
пользоваться свойствами движений и преобразований при решении задач.
В повседневной жизни и при изучении других предметов:
-
применять свойства движений и применять подобие для построений и вычислений.
Векторы и координаты на плоскости
-
Свободно оперировать понятиями вектор, сумма, разность векторов, произведение вектора на число, скалярное произведение векторов, координаты на плоскости, координаты вектора;
-
владеть векторным и координатным методом на плоскости для решения задач на вычисление и доказательства;
-
выполнять с помощью векторов и координат доказательство известных ему геометрических фактов (свойства средних линий, теорем о замечательных точках и т.п.) и получать новые свойства известных фигур;
-
использовать уравнения фигур для решения задач и самостоятельно составлять уравнения отдельных плоских фигур.
В повседневной жизни и при изучении других предметов:
-
использовать понятия векторов и координат для решения задач по физике, географии и другим учебным предметам.
История математики
-
Понимать математику как строго организованную систему научных знаний, в частности владеть представлениями об аксиоматическом построении геометрии и первичными представлениями о неевклидовых геометриях;
-
рассматривать математику в контексте истории развития цивилизации и истории развития науки, понимать роль математики в развитии России.
Методы математики
-
Владеть знаниями о различных методах обоснования и опровержения математических утверждений и самостоятельно применять их;
-
владеть навыками анализа условия задачи и определения подходящих для решения задач изученных методов или их комбинаций;
-
характеризовать произведения искусства с учетом математических закономерностей в природе, использовать математические закономерности в самостоятельном творчестве.
ӀӀ. Содержание учебного предмета, курса
Содержание курса математики в 5-6 классах
Арифметика
Натуральные числа
Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий. Понятие о степени с натуральным показателем. Квадрат и куб числа. Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическими способами. Делители и кратные. Наибольший общий делитель; наименьшее общее кратное. Свойства делимости. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком.
Дроби
Обыкновенные дроби. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части. Десятичные дроби. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной. Отношение. Пропорция; основное свойство пропорции. Проценты; нахождение процентов от величины и величины по её процентам; выражение отношения в процентах. Решение текстовых задач арифметическими способами.
Рациональные числа
Положительные и отрицательные числа, модуль числа. Изображение чисел точками координатной прямой; геометрическая интерпретация модуля числа. Множество целых чисел. Множество рациональных чисел. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий.
Измерения, приближения, оценки. Зависимости между величинами
Единицы измерения длины, площади, объёма, массы, времени, скорости. Примеры зависимостей между величинами скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость и др. Представление зависимостей в виде формул. Вычисления по формулам. Решение текстовых задач арифметическими способами.
Элементы алгебры
Использование букв для обозначения чисел; для записи свойств арифметических действий. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Уравнение, корень уравнения. Нахождение неизвестных компонентов арифметических действий. Декартовы координаты на плоскости. Построение точки по её координатам, определение координат точки на плоскости.
Описательная статистика. Комбинаторика. Множества
Представление данных в виде таблиц, диаграмм. Решение комбинаторных задач перебором вариантов. Множество, элемент множества.
Наглядная геометрия
Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, правильный многоугольник, окружность, круг. Четырёхугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Изображение геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины. Угол. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Равновеликие фигуры. Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники, правильные многогранники. Примеры развёрток многогранников, цилиндра и конуса. Понятие объёма; единицы объёма. Объём прямоугольного параллелепипеда, куба. Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.
История математики
История формирования понятия числа: натуральные числа, дроби, недостаточность рациональных чисел для геометрических измерений, иррациональные числа. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Появление отрицательных чисел и нуля. Л. Магницкий. Л. Эйлер.
Содержание курса математики в 7-9 классах
Арифметика
Рациональные числа
Расширение множества натуральных чисел до множества целых.
Множества целых чисел до множества рациональных. Рациональное число
как отношение ![]() , где m -
целое число, n - натуральное. Степень с целым показателем.
, где m -
целое число, n - натуральное. Степень с целым показателем.
Действительные числа
Квадратный корень из числа. Корень третьей степени. Запись корней с помощью степени с дробным показателем. Понятие об иррациональном числе. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел. Множество действительных чисел; представление действительных чисел бесконечными десятичными дробями. Сравнение действительных чисел. Координатная прямая. Изображение чисел точками координатной прямой. Числовые промежутки.
Измерения, приближения, оценки
Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя - степени десяти в записи числа. Приближённое значение величины, точность приближения. Прикидка и оценка результатов вычислений.
Алгебра
Алгебраические выражения
Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество.
Степень с натуральным показателем и её свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращённого умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Квадратный трёхчлен; разложение квадратного трёхчлена на множители.
Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и её свойства.
Рациональные выражения и их преобразования. Доказательство тождеств.
Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям.
Уравнения
Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений.
Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к линейным и квадратным. Примеры решения уравнений третьей и четвёртой степеней. Решение дробно-рациональных уравнений.
Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах.
Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Примеры решения систем нелинейных уравнений с двумя переменными.
Решение текстовых задач алгебраическим способом.
Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными; угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными.
Неравенства
Числовые неравенства и их свойства.
Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы неравенств с одной переменной.
Функции
Основные понятия
Зависимости между величинами. Понятие функции. Область определения и множество значений функции. Способы задания функции. График функции. Свойства функций, их отображение на графике. Примеры графиков зависимостей, отражающих реальные процессы.
Числовые функции
Функции, описывающие прямую и обратную пропорциональные
зависимости, их графики и свойства. Линейная функция, её график и
свойства. Квадратичная функция, её график и свойства. Степенные
функции с натуральными показателями 2 и 3, их графики и свойства.
Графики функций y=![]() , y=
, y=![]() , у =| x|.
, у =| x|.
Числовые последовательности
Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена.
Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых n-х членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
Вероятность и статистика.
Описательная статистика
Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании.
Случайные события и вероятность
Понятие о случайном опыте и случайном событии. Частота случайного события. Статистический подход к понятию вероятности. Вероятности противоположных событий. Независимые события. Умножение вероятностей. Достоверные и невозможные события. Равновозможные события. Классическое определение вероятности.
Комбинаторика
Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал.
Логика и множества
Теоретико-множественные понятия
Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств, разность множеств.
Иллюстрация отношений между множествами с помощью диаграмм Эйлера - Венна.
Элементы логики
Понятие о равносильности, следовании, употребление логических связок если ..., то ..., в том и толь-ко в том случае, логические связки и, или.
История математики
История формирования понятия числа: натуральные числа, дроби, недостаточность рациональных чисел для геометрических измерений, иррациональные числа. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Появление отрицательных чисел и нуля. Л. Магницкий. Л. Эйлер.
Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рождение буквенной символики. П. Ферма, Ф. Виет, Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений, неразрешимость в радикалах уравнений степени, большей четырёх. Н. Тарталья, Дж. Кардано, Н. X. Абель, Э. Галуа.
Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Ферма. Примеры различных систем координат на плоскости.
Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске.
Истоки теории вероятностей: страховое дело, азартные игры. П. Ферма и Б. Паскаль. Я. Бернулли. А. Н. Колмогоров.
Геометрия
Наглядная геометрия
Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примеры развёрток многогранников, цилиндра и конуса.
Понятие объёма; единицы объёма. Объём прямоугольного параллелепипеда, куба.
Геометрические фигуры
Прямые и углы. Точка, прямая, плоскость. Отрезок, луч. Угол. Виды углов. Вертикальные и смежные углы. Биссектриса угла.
Параллельные и пересекающиеся прямые. Перпендикулярные прямые. Теоремы о параллельности и перпендикулярности прямых. Перпендикуляр и наклонная к прямой. Серединный перпендикуляр к отрезку.
Геометрическое место точек. Свойства биссектрисы угла и серединного перпендикуляра к отрезку.
Треугольник. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Неравенство треугольника. Соотношения между сторонами и углами треугольника.
Сумма углов треугольника. Внешние углы треугольника. Теорема Фалеса. Подобие треугольников. Признаки подобия треугольников. Теорема Пифагора. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0 до 180°; приведение к острому углу. Решение прямоугольных треугольников. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Решение треугольников: теорема косинусов и теорема синусов. Замечательные точки треугольника.
Четырёхугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции.
Многоугольник. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники.
Окружность и круг. Дуга, хорда. Сектор, сегмент. Центральный угол, вписанный угол, величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, их свойства. Вписанные и описанные многоугольники. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные окружности правильного многоугольника.
Геометрические преобразования. Понятие о равенстве фигур. Понятие о движении: осевая и центральная симметрии, параллельный перенос, поворот. Понятие о подобии фигур и гомотетии.
Построения с помощью циркуля и линейки. Основные за-дачи на построение: деление отрезка пополам; построение угла, равного данному; построение треугольника по трём сторонам; построение перпендикуляра к прямой; построение биссектрисы угла; деление отрезка на n равных частей.
Решение задач на вычисление, доказательство и построение с использованием свойств изученных фигур.
Измерение геометрических величин
Длина отрезка. Рас-стояние от точки до прямой. Расстояние между параллельными прямыми.
Периметр многоугольника.
Длина окружности, число π; длина дуги окружности.
Градусная мера угла, соответствие между величиной центрального угла и длиной дуги окружности.
Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции. Площадь многоугольника. Площадь круга и площадь сектора. Соотношение между площадями подобных фигур.
Решение задач на вычисление и доказательство с использованием изученных формул.
Координаты
Уравнение прямой. Координаты середины отрезка. Формула расстояния между двумя точками плоскости. Уравнение окружности.
Векторы
Длина (модуль) вектора. Равенство векторов. Коллинеарные векторы. Координаты вектора. Умножение вектора на число, сумма векторов, разложение вектора по двум неколлинеарным векторам. Скалярное произведение векторов.
Теоретико-множественные понятия
Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Подмножество. Объединение и пересечение множеств.
Элементы логики
Определение. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример.
Понятие о равносильности, следовании, употребление логических связок если ...,то ..., в том и только в том случае, логические связки и, или.
Геометрия в историческом развитии
От землемерия к геометрии. Пифагор и его школа. Фалес. Архимед. Построение правильных многоугольников. Трисекция угла. Квадратура круга. Удвоение куба. История числа π. Золотое сечение. «Начала» Евклида. Л. Эйлер. Н. И. Лобачевский. История пятого постулата.
Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Ферма. Примеры различных систем координат на плоскости.
ӀӀӀ. Тематическое планирование
Математика, 5 класс
(к УМК Математика, 5 кл.: учебник для общеобразовательных учреждений/ Н.В. Виленкин, В.И.Жохов, А.С.Чесноков, С.И. Шварцбурд, - М.: Мнемозина, 2014.)
№ урока
Тема урока
Кол-во часов
§ 1. Натуральные числа и шкалы
16
1
Повторение
1
2-3
Обозначение натуральных чисел
2
4
Обозначение натуральных чисел. Классы и разряды
1
5
Отрезок
1
6
Отрезок. Длина отрезка
1
7
Треугольник
1
8
Плоскость. Прямая.
1
9
Плоскость. Прямая. Луч
1
10
Шкалы и координаты
1
11
Шкалы и координаты. Единицы массы
1
12
Координатный луч
1
13
Меньше или больше
1
14
Меньше или больше. Двойные неравенства
1
15
Меньше или больше. Сравнение отрезков
1
16
Контрольная работа №1 по теме «Натуральные числа и шкалы»
1
§ 2. Сложение и вычитание натуральных чисел
10
17
Сложение натуральных чисел
1
18
Сложение натуральных чисел и его свойства
1
19
Сложение натуральных чисел. Разложение числа по разрядам
1
20
Сложение натуральных чисел. Периметр многоугольника
1
21
Сложение натуральных чисел и его свойства
1
22
Вычитание
1
23
Вычитание. Свойства вычитания
1
24-25
Вычитание. Решение текстовых задач
2
26
Контрольная работа №2 по теме «Сложение и вычитание натуральных чисел»
1
§ 3. Числовые и буквенные выражения
11
27
Числовое выражение
1
28-29
Буквенное выражение и его числовое значение
2
30
Буквенное выражение. Буквенная запись свойств сложения
1
31-32
Буквенное выражение. Буквенная запись свойств сложения и вычитания
2
33-34
Уравнение
2
35-36
Уравнение. Решение текстовых задач с помощью уравнений
2
37
Контрольная работа №3 по теме «Числовые и буквенные выражения»
1
§ 4. Умножение и деление натуральных чисел
16
38-39
Умножение натуральных чисел и его свойства
2
40-42
Умножение натуральных чисел. Решение текстовых задач, уравнений
3
43-44
Деление натуральных чисел
2
45-49
Деление натуральных чисел. Решение текстовых задач, уравнений
5
50-52
Деление с остатком
3
53
Контрольная работа №4 по теме «Умножение и деление натуральных чисел»
1
§ 5. Упрощение выражений
11
54-58
Упрощение выражений
5
59-61
Порядок выполнения действий
3
62-63
Степень числа. Квадрат и куб числа
2
64
Контрольная работа №5 по теме «Упрощение выражений»
1
§ 6. Площади и объемы
12
65-66
Формулы
2
67-68
Площадь. Формула площади прямоугольника
2
69-71
Единицы измерения площадей
3
72
Прямоугольный параллелепипед
1
73-75
Объемы. Объем прямоугольного параллелепипеда
3
76
Контрольная работа №6 по теме «Площади и объемы»
1
§ 7. Обыкновенные дроби
23
77-78
Окружность и круг
2
79-81
Доли, обыкновенные дроби
3
82
Основные задачи на дроби
1
83-85
Сравнение дробей
3
86-87
Правильные и неправильные дроби
2
88
Контрольная работа №7 по теме «Обыкновенные дроби»
1
89-91
Сложение и вычитание дробей с одинаковыми знаменателями
3
92-93
Деление и дроби
2
94-95
Смешанные числа
2
96-98
Сложение и вычитание смешанных чисел
3
99
Контрольная работа №8 по теме «Смешанные числа»
1
§ 8. Сложение и вычитание десятичных дробей
13
100-101
Десятичная запись дробных чисел
2
102-104
Сравнение десятичных дробей
3
105-109
Сложение и вычитание десятичных дробей
5
110-111
Приближенные значения чисел. Округление чисел
2
112
Контрольная работа №9 по теме «Сложение и вычитание десятичных дробей»
1
§ 9. Умножение и деление десятичных дробей
26
113
Умножение десятичных дробей на натуральные числа
1
114
Умножение десятичных дробей на натуральные числа. Упрощение выражений
1
115
Умножение десятичных дробей на натуральные числа. Решение текстовых задач, уравнений
1
116
Деление десятичных дробей на натуральные числа
1
117
Деление десятичных дробей на натуральные числа. Упрощение числовых и буквенных выражений
1
118-119
Деление десятичных дробей на натуральные числа. Решение текстовых задач, уравнений
2
120
Умножение и деление десятичных дробей на натуральные числа
1
121
Контрольная работа №10 по теме «Умножение и деление десятичной дроби на натуральное число»
1
122-126
Умножение десятичных дробей
5
127-130
Деление на десятичную дробь
4
131
Итоговое занятие III четверти.
1
132-133
Деление на десятичную дробь
2
134-137
Среднее арифметическое
4
138
Контрольная работа №11 по теме «Умножение и деление десятичных дробей»
1
§ 10. Инструменты для вычислений и измерений
17
139-140
Микрокалькулятор
2
141-142
Проценты
2
143-145
Основные задачи на проценты
3
146
Контрольная работа №12 по теме «Проценты»
1
147-149
Угол. Прямой и развернутый угол. Чертежный треугольник
3
150-152
Измерение углов. Транспортир
3
153-154
Круговые диаграммы
2
155
Контрольная работа №13 по теме «Угол. Транспортир»
1
Итоговое повторение
20
156-157
Повторение. Натуральные числа
2
158-159
Повторение. Площади и объемы
2
160-162
Повторение. Обыкновенные дроби
3
163-165
Повторение. Десятичные дроби
3
166-167
Повторение. Проценты
2
168-169
Повторение. Углы
2
170
Контрольная работа №14 «Итоговая контрольная работа за курс математики 5-го класса»
1
171-175
Итоговое повторение
5
Математика, 6 класс
(к УМК Математика, 6 кл.: учебник для общеобразовательных учреждений/ Н.В. Виленкин, В.И.Жохов, А.С.Чесноков, С.И. Шварцбурд, - М.: Мнемозина, 2014.)
1-3
Делители и кратные
3
4-6
Признаки делимости на 10, на 5 и на 2
3
7-8
Признаки делимости на 9 и на 3
2
9-10
Простые и составные числа
2
11-12
Разложение на простые множители
2
13-15
Наибольший общий делитель. Взаимно простые числа
3
16-19
Наименьшее общее кратное
4
20
Контрольная работа №1
1
§ 2. Сложение и вычитание дробей с разными знаменателями
22
21-22
Основное свойство дроби
2
23-25
Сокращение дробей
3
26-28
Приведение дробей к общему знаменателю
3
29-34
Сравнение, сложение и вычитание дробей с разными знаменателями
6
35
Контрольная работа № 2
1
36-41
Сложение и вычитание смешанных чисел
6
42
Контрольная работа № 3
1
§ 3. Умножение и деление обыкновенных дробей
32
43-46
Умножение дробей
4
47
Итоговый урок по материалу I четверти
1
48-51
Нахождение дроби от числа
4
52-56
Применение распределительного свойства умножения
5
57
Контрольная работа № 4
1
58-59
Взаимно обратные числа
2
60-64
Деление
5
65
Контрольная работа № 5
1
66-70
Нахождение числа по его дроби
5
71-73
Дробные выражения
3
74
Контрольная работа № 6
1
§ 4. Отношения и пропорции
19
75-79
Отношения
5
80-81
Пропорции
2
82
Повторение. Решение задач. Обобщение материала II четверти
1
83-85
Прямая и обратная пропорциональные зависимости
3
86
Контрольная работа № 7
1
87-88
Масштаб
2
89-90
Длина окружности и площадь круга
2
91-92
Шар
2
93
Контрольная работа № 8
1
§ 5. Положительные и отрицательные числа
13
94-96
Координаты на прямой
3
97-98
Противоположные числа
2
99-100
Модуль числа
2
101-103
Сравнение чисел
3
104
Изменение величин
2
106
Контрольная работа № 9
1
§ 6. Сложение и вычитание положительных и отрицательных чисел
11
107-108
Сложение чисел с помощью координатной прямой
2
109-110
Сложение отрицательных чисел
2
111-113
Сложение чисел с разными знаками
3
114-116
Вычитание
3
117
Контрольная работа № 10
1
§ 7. Умножение и деление положительных и отрицательных чисел
12
118-120
Умножение
3
121-123
Деление
3
124-125
Рациональные числа
2
126
Контрольная работа № 11
1
127-129
Свойства действий с рациональными числами
3
§ 8. Решение уравнений
15
130-131
Раскрытие скобок
2
132-133
Урок повторения и обобщения по материалу III четверти
2
134-135
Коэффициент
2
136-138
Подобные слагаемые
3
139
Контрольная работа № 12
1
140-143
Решение уравнений
4
144
Контрольная работа № 13
1
§ 9. Координаты на плоскости
13
145-146
Перпендикулярные прямые
2
147-148
Параллельные прямые
2
149-151
Координатная плоскость
3
152-153
Столбчатые диаграммы
2
154-156
Графики
3
157
Контрольная работа № 14
1
Повторение
18
158-159
Повторение. Признаки делимости
2
160-161
Повторение. Сложение и вычитание дробей
2
162-163
Повторение. Умножение и деление обыкновенных дробей
2
164-165
Повторение. Отношения и пропорции
2
166-167
Повторение. Положительные и отрицательные числа
2
168-169
Повторение. Решение уравнений
2
170
Итоговая контрольная работа
1
171-175
Обобщающие уроки
5
Алгебра, 7 класс
(к УМК Макарычев Ю. Н. Алгебра, 7 кл.: учебник для общеобразовательных организаций / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под редакцией С. А. Теляковского. - М.: Просвещение, 2014.)
Глава I. Выражения, тождества, уравнения
22
1-5
Выражения
5
6-9
Преобразование выражений
4
10
Контрольная работа № 1
1
11-17
Уравнения с одной переменной
7
18-21
Статистические характеристики
4
22
Контрольная работа № 2
1
Глава II. Функции
11
23-27
Функции и их графики
5
28-32
Линейная функция
5
33
Контрольная работа № 3
1
Глава III. Степень с натуральным показателем
11
34-38
Степень и её свойства
5
39-43
Одночлены
5
44
Контрольная работа № 3
1
Глава IV. Многочлены
17
45-47
Сумма и разность многочленов
3
48-53
Произведение одночлена и многочлена
6
54
Контрольная работа № 5
1
55-60
Произведение многочленов
6
61
Контрольная работа № 6
1
Глава V. Формулы сокращённого умножения
19
62-66
Квадрат суммы и квадрат разности
5
67-72
Разность квадратов. Сумма и разность кубов
6
73
Контрольная работа № 7
1
74-79
Преобразование целых выражений
6
80
Контрольная работа № 8
1
Глава VI. Системы линейных уравнений
16
81-85
Линейные уравнения с двумя переменными и их системы
5
86-95
Решение систем линейных уравнений
10
96
Контрольная работа № 9
1
97-101
Повторение
5
102
Итоговая контрольная работа
1
103-105
Итоговые уроки
3
Геометрия, 7 класс
(к УМК Геометрия: 7-9 кл. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. - М.: Просвещение, 2011.)
Глава I . Начальные геометрические сведения
11
1
Прямая и отрезок
1
2
Луч и угол
1
3
Сравнение отрезков и углов
1
4-5
Измерение отрезков
2
6
Измерение углов
1
7
Смежные и вертикальные углы
1
8
Перпендикулярные прямые
1
9
Решение задач
1
10
Контрольная работа № 1 по теме «Измерение отрезков и углов»
1
11
Анализ контрольной работы. Работа над ошибками
1
Глава II. Треугольники
18
12
Треугольники
1
13-14
Первый признак равенства треугольников
2
15
Перпендикуляр к прямой
1
16
Медианы, биссектрисы и высоты треугольника
1
17-18
Свойства равнобедренного треугольника
2
19-20
Второй признак равенства треугольников
2
21
Третий признак равенства треугольников
1
22
Решение задач на применение признаков равенства треугольников
1
23
Окружность
1
24-25
Задачи на построение
2
26-27
Решение задач на применение признаков равенства треугольников
2
28
Контрольная работа № 2 по теме «Треугольники»
1
29
Анализ контрольной работы. Работа над ошибками
1
Глава III. Параллельные прямые
13
30-31
Признаки параллельности двух прямых
2
32
Практические способы построения параллельных прямых
1
33
Решение задач по теме «Признаки параллельности прямых»
1
34
Аксиома параллельных прямых
1
35-36
Свойства параллельных прямых
2
37-40
Решение задач по теме «Параллельные прямые»
4
41
Контрольная работа № 3 по теме «Параллельные прямые»
1
42
Анализ контрольной работы. Работа над ошибками
1
Глава IV. Соотношения между сторонами и углами треугольника
20
43-44
Сумма углов треугольника
2
45-46
Соотношения между сторонами и углами треугольника
2
47
Неравенство треугольника
1
48
Решение задач
1
49
Контрольная работа №4 по теме «Соотношения между сторонами и углами треугольника»
1
50
Анализ контрольной работы. Работа над ошибками
1
51-52
Прямоугольные треугольники и некоторые их свойства
2
53-54
Признаки равенства прямоугольных треугольников
2
55
Расстояние от точки до прямой. Расстояние между параллельными прямыми
1
56-58
Построение треугольника по трём элементам
3
59-60
Решение задач
2
61
Контрольная работа № 5 по теме «Прямоугольный треугольник. Построение треугольника по трём элементам»
1
62
Анализ контрольной работы. Работа над ошибками
1
Повторение. Решение задач
6
63
Повторение темы «Начальные геометрические сведения»
1
64
Повторение темы «Признаки равенства треугольников. Равнобедренный треугольник»
1
65
Повторение темы «Параллельные прямые»
1
66
Повторение темы «Соотношения между сторонами и углами треугольника»
1
67
Контрольная работа № 6 (итоговая)
1
68
Решение задач
1
Алгебра, 8 класс
(к УМК Макарычев Ю. Н. Алгебра, 8 кл.: учебник для общеобразовательных организаций / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Не-шков, С. Б. Суворова; под редакцией С. А. Теляковского. - М.: Просвещение, 2014.)
Глава I. Рациональные дроби
23
1-5
Рациональные дроби и их свойства
5
6-11
Сумма и разность дробей
6
12
Контрольная работа № 1
1
13-22
Произведение и частное дробей
10
23
Контрольная работа № 2
1
Глава II. Квадратные корни
19
24-25
Действительные числа
2
26-30
Арифметический квадратный корень
5
31-33
Свойства арифметического квадратного корня
3
34
Контрольная работа № 3
1
35-41
Применение свойств арифметического квадратного корня
7
42
Контрольная работа № 4
1
Глава III. Квадратные уравнения
21
43-52
Квадратное уравнение и его корни
10
53
Контрольная работа № 5
1
54-62
Дробные рациональные уравнения
9
63
Контрольная работа № 6
1
Глава IV. Неравенства
20
64-71
Числовые неравенства и их свойства
8
72
Контрольная работа № 7
1
73-82
Неравенства с одной переменной и их системы
10
83
Контрольная работа № 8
1
Глава V. Степень с целым показателем. Элементы статистики
11
84-89
Степень с целым показателем и её свойства
6
90
Контрольная работа № 9
1
91-94
Элементы статистики
4
95-101
Повторение
7
102
Итоговая контрольная работа
1
103
Итоговый зачёт
1
104-105
Итоговые уроки
2
Геометрия, 8 класс
(к УМК Геометрия: 7-9 кл. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. - М.: Просвещение, 2011.)
Глава I. Четырёхугольники
14
1-2
Многоугольники
2
3-8
Параллелограмм и трапеция
6
9-12
Прямоугольник, ромб, квадрат
4
13
Решение задач
1
14
Контрольная работа № 1
1
Глава II. Площадь
14
15-16
Площадь многоугольника
2
17-22
Площади параллелограмма, треугольника и трапеции
6
23-25
Теорема Пифагора
3
26-27
Решение задач
2
28
Контрольная работа № 2
1
Глава III. Подобные треугольники
19
29-30
Определение подобных треугольников
2
31-35
Признаки подобия треугольников
5
36
Контрольная работа № 3
1
37-43
Применение подобия к доказательству теорем и решению задач
7
44-46
Соотношения между сторонами и углами прямоугольного треугольника
3
47
Контрольная работа № 4
1
Глава IV. Окружность
17
48-50
Касательная к окружности
3
51-54
Центральные и вписанные углы
4
55-57
Четыре замечательные точки треугольника
3
58-61
Вписанная и описанная окружности
4
62-63
Решение задач
2
64
Контрольная работа № 5
1
65-68
Повторение. Решение задач
4
Алгебра, 9 класс
(к УМК Макарычев Ю. Н. Алгебра, 9 кл.: учебник для общеобразовательных организаций / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под редакцией С. А. Теляковского. - М.: Просвещение, 2014.)
Глава I. Квадратичная функция
22
1-5
Функции и их свойства
5
6-9
Квадратный трёхчлен
4
10
Контрольная работа № 1
1
11-18
Квадратичная функция и её график
8
19-21
Степенная функция. Корень n-й степени
3
22
Контрольная работа № 2
1
Глава II. Уравнения и неравенства с одной переменной
14
23-30
Уравнения с одной переменной
8
31-35
Неравенства с одной переменной
5
36
Контрольная работа № 3
1
Глава III. Уравнения и неравенства с двумя переменными
17
37-46
Уравнения с двумя переменными и их системы
10
47-52
Неравенства с двумя переменными и их системы
6
53
Контрольная работа № 4
1
Глава IV. Арифметическая и геометрическая прогрессии
15
54-60
Арифметическая прогрессия
7
61
Контрольная работа № 5
1
62-67
Геометрическая прогрессия
6
68
Контрольная работа № 6
1
Глава V. Элементы комбинаторики и теории вероятностей
13
69-77
Элементы комбинаторики
9
78-80
Начальные сведения из теории вероятностей
3
81
Контрольная работа № 7
1
82-102
Повторение
21
103-104
Итоговая контрольная работа
2
Геометрия, 9 класс
(к УМК Геометрия: 7-9 кл. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. - М.: Просвещение, 2011.)
Глава I. Векторы
8
1-2
Понятие вектора
2
3-5
Сложение и вычитание векторов
3
6-8
Умножение вектора на число. Применение векторов к решению задач
3
Глава II. Метод координат
10
9-10
Координаты вектора
2
11-12
Простейшие задачи в координатах
2
13-15
Уравнения окружности и прямой
3
16-17
Решение задач
2
18
Контрольная работа № 1
1
Глава III. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
11
19-21
Синус, косинус, тангенс, котангенс угла
3
22-25
Соотношения между сторонами и углами треугольника
4
26-27
Скалярное произведение векторов
2
28
Решение задач
1
29
Контрольная работа № 2
1
Глава IV. Длина окружности и площадь круга
12
30-33
Правильные многоугольники
4
34-37
Длина окружности и площадь круга
4
38-40
Решение задач
3
41
Контрольная работа № 3
1
Глава V. Движения
8
42-44
Понятие движения
3
45-47
Параллельный перенос и поворот
3
48
Решение задач
1
49
Контрольная работа № 4
1
Глава VI. Начальные сведения из стереометрии
8
50-53
Многогранники
4
54-57
Тела и поверхности вращения
4
58-59
Об аксиомах планиметрии
2
60-68
Повторение. Решение задач
9
1 Здесь и далее - распознавать конкретные примеры общих понятий по характерным признакам, выполнять действия в соответствии с определением и простейшими свойствами понятий, конкретизировать примерами общие понятия.
2 Здесь и далее - знать определение понятия, уметь пояснять его смысл, уметь использовать понятие и его свойства при проведении рассуждений, доказательств, решении задач.
3 Здесь и далее - распознавать конкретные примеры общих понятий по характерным признакам, выполнять действия в соответствии с определением и простейшими свойствами понятий, конкретизировать примерами общие понятия.
4 Здесь и далее - знать определение понятия, уметь пояснять его смысл, уметь использовать понятие и его свойства при проведении рассуждений, доказательств, решении задач.
5</ Здесь и далее - знать определение понятия, знать и уметь доказывать свойства (признаки, если они есть) понятия, характеризовать связи с другими понятиями, представляя одно понятие как часть целостного комплекса, использовать понятие и его свойства при проведении рассуждений, доказательств, решении задач.