Методическая разработка урока геометрии в 8 классе по теме 'Ромб и его свойства'

МБОУ СОШ № 12 ст. Кавказская

Методическая разработка урока геометрии в 8 классе по теме

"Ромб и его свойства"

Учитель математики

Юдт Татьяна Владимировна

Тип урока - комбинированный

Цели урока

- введение понятия ромба и изучение его свойств;

- формирование навыков решения задач на применение нового и ранее изученного материала.

Задачи урока

Образовательные:

- повторить материал и углубить знания по теме «Параллелограмм»;

- ввести понятие ромба, ;

- сформулировать и доказать свойства и признаки ромба;

- отрабатывать навык решения задач по данной теме.

Развивающие:

- развивать навыки анализа, сравнения материала, проведения аналогии;

- развивать навык выдвигать гипотезы и доказывать их;

- содействовать развитию умений осуществлять самооценку учебной деятельности.

Воспитательный аспект:

- создать у учащихся положительную мотивацию к уроку геометрии путем вовлечения каждого ученика в активную деятельность;

- воспитывать потребность оценивать свою деятельность и работу товарищей;

- помочь осознать ценность совместной деятельности;

- воспитывать культуру речи, внимание к точности формулировок.

Оборудование: мультимедийный проектор, экран, карточки заданий.

Ход урока:

1. Организационный момент.

Приветствие учащихся. Сообщение темы, целей и задач урока.

2.Актуализация знаний учащихся (дифференцированный подход). Повторим свойства и признаки параллелограмма:

1 группа учащихся( «3» )

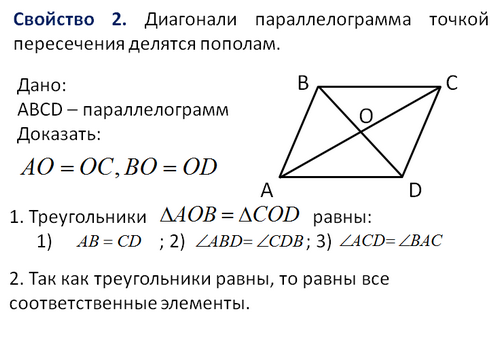
Назовиете признаки параллелограмма

2 группа учащихся ( «4» ) устно решает задачу

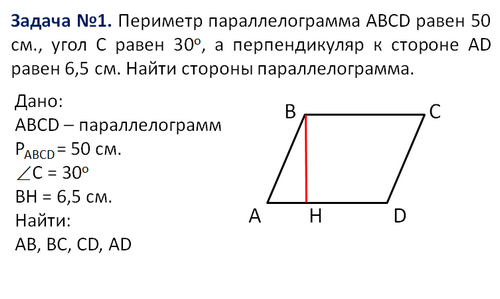
3 группа учащихся ( «5» )

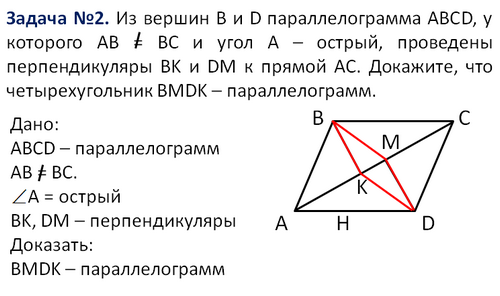
2.Изложение нового материала

По определению, ромб - это параллелограмм, все стороны которого равны.

Следовательно все свойства параллелограмма присущи ромбу. Как то:

• 1. Противоположные стороны ромба равны.

• 2. Диагонали точкой пересечения делятся пополам.

Свойства ромба

1. Поскольку ромб - это параллелограмм, то все верны для ромба.

Помимо этого:

2. Диагонали ромба перпендикулярны.

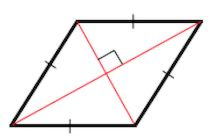
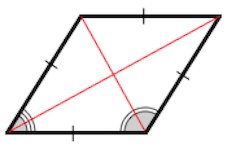
3. Диагонали ромба являются биссектрисами его углов.

4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.

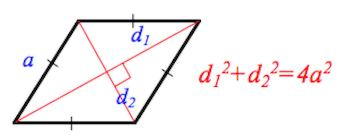
Видим, что диагонали ромба делят его на 4 равных прямоугольных треугольника.

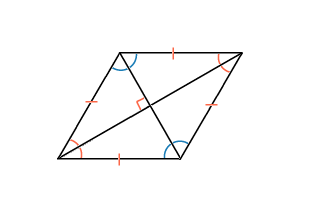
Признаки ромба

Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:

1. Все стороны параллелограмма равны между собой.

2. Диагонали пересекаются под прямым углом.

3. Диагонали параллелограмма являются биссектрисами его углов.

3.Решение задач по теме урока

Воспользуемся свойствами ромба для решения задач.

№1. Найдите меньшую диагональ ромба, стороны которого равны 2 , а острый угол равен 60° .

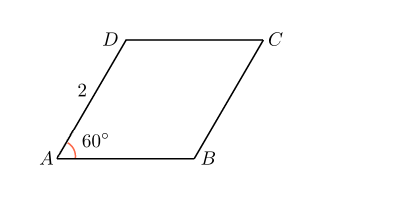
Проведите меньшую диагональ ромба и рассмотрите треугольник . Поскольку , а угол равен , треугольник - равносторонний. Следовательно, меньшая диагональ ромба равна .

№2. Найдите высоту ромба, сторона которого равна 3, а острый угол равен 60° .

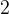
Один из подходов к решению задач по геометрии - метод площадей. Он состоит в том, что площадь фигуры выражается двумя разными способами, а затем из полученного уравнения находится неизвестная величина.

Пусть - сторона ромба. Тогда

Отсюда .

№3. Диагонали ромба относятся как 3:4 . Периметр ромба равен 200 . Найдите высоту ромба.

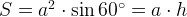
Пусть диагонали ромба равны и .
Диагонали ромба перпендикулярны, значит, треугольник - прямоугольный.
По теореме Пифагора
,
,
Отсюда .
Поскольку периметр равен ,

, , а диагонали ромба равны и .

Нам надо найти высоту ромба.
Давайте запишем, чему равна площадь ромба. С одной стороны, . С другой стороны, площадь ромба складывается из площадей двух равных треугольников и , то есть равна .
Отсюда .

Ответ: .

4. Физкультминутка.

Раз - подняться, потянуться,

Два - нагнуться, разогнуться,

Три - в ладоши три хлопка,

Головою - три кивка.

Пять - руками помахать,

Шесть - на место тихо сесть.

5. Итог урока.

6. Домашнее задание.

«3»

• Периметр ромба 20 см. Найдите стороны ромба

• Один из углов ромба 70 градусов. Определите остальные углы ромба.

Диагональ АС ромба АВСД равна 10 см, ВД равна 6 см. Какова длина отрезков АО и ВО, если О - точка пересечения диагоналей

«4»

• В ромбе АВСД угол А равен 140 градусам. Чему равны углы треугольника АОВ?

• Найти периметр ромба ABCD, если известно, что угол ВАС равен 60°.

«5»

• Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых равен 30°, а второй на 30° больше первого.

• В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и N. Найдите угол АNВ, если ∠АМС=120°.