- Учителю
- Урок поматематике для 6 класса «Сложение чисел с разными знаками»
Урок поматематике для 6 класса «Сложение чисел с разными знаками»
Тема: «Сложение чисел с разными знаками».
(6 класс)
Цели урока:
- научить складывать отрицательные числа, числа с разными знаками
и противоположные числа;
- развитие познавательной активности, творческих способностей,
умения оценивать друг друга;
- формирование умения самостоятельно мыслить.
Ход урока.
Устная работа:
1. Как сложить две десятичные дроби?
(Сложение по разрядам, запятая - под запятой.)
2. Как сложить две обыкновенные дроби?
( - найти общий знаменатель;
- найти дополнительные множители;
- выполнить действие.)
3. Вычислить: 4 + 1,5 =
6,3 + 3,4 =
7,2 - 4,1 =
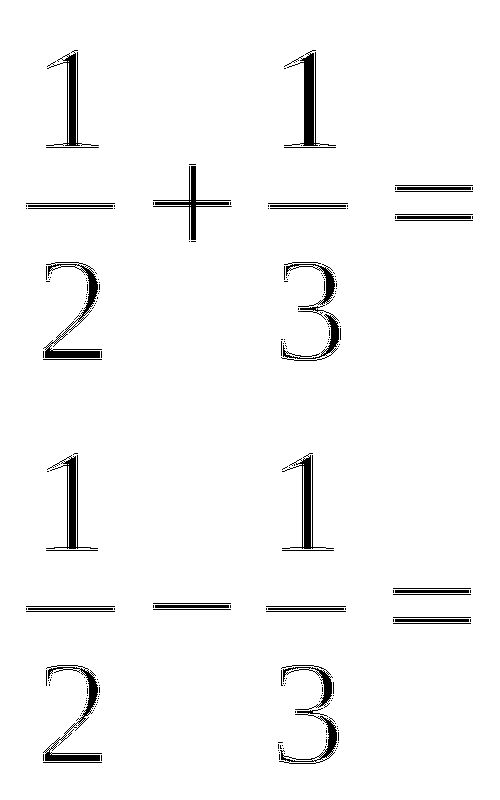
4. Как сравнить десятичные дроби?
( по разрядам.)
5. Как сравнить обыкновенные дроби, если:
а) знаменатели равны;
(из двух дробей с равными знаменателями больше та,
числитель которой - больше)
б) числители равны;
(из двух дробей с равными числителями больше та,
числитель которой - меньше)
в) и числитель, и знаменатель - разные.
(если числители и знаменатели дробей разные, то
приводим их к общему знаменателю, а затем
сравниваем их также как с равными знаменателями)
6. Сравнить: 1,3 и 2,4;
3,15 и 3,17;
![]() и
и ![]() ;
;
![]() и
и ![]() ;
;
![]() и
и ![]() .
.
7. Какие числа называются отрицательными?
(числа со знаком «минус»)
8. Какие числа называются положительными?
(числа со знаком «плюс»)
9. Какие числа называются противоположными?
(числа, находящиеся на одинаковом расстоянии от
нуля, но в противоположном направлении.)
10. Назовите положительные, отрицательные и противоположные числа:
-5,2; 35; 7,8; 5,2; -19; 24; -1,7; 28,6; 19; ½; -16,7; 107; 293; -½; 25,6; 15,015; -¾; 27½; -5,2; ¼; -35.
11. Когда возникли отрицательные числа? Где? Какие действия с ними умели выполнять древние? (приложение, слайд №5)
- Отрицательные числа появились приблизительно 2100 лет тому назад в Древнем Китае. Древние толковали о долге (отрицательные числа) и имуществе (положительные числа). Долгое время такие числа считали «несуществующими» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество - долг» приводило к недоумениям: можно сложить или вычесть «имущество» или «долги», но как понимать произведение «имущества» и «долга»? Однако несмотря на такие сомнения и недоумения действия сложения, вычитания, умножения и деления выполнялись, правила для чего были предложены греческим математиком Диофантом еще в III в нашей эры.
Рассмотрим следующие задачи: (приложение, слайд № 6-10)
1. В книге доходов и расходов купца сделаны следующие записи:
прибыль
200
500
600
итого
?
убытки
500
200
300
?
Необходимо выяснить прибыльное ли дело у купца или он имеет долг?
Решение: 1. 200 + 500 + 600 = 1300 (прибыль)
2. (-500) + (- 200) + (- 300) = -1000 (убыток)
3. 1300 + (- 1000) = 300 (прибыль)
прибыль
200
500
600
итого
1300
убытки
500
200
300
1000
Ответ: дело у купца прибыльное.
2. «Игра в кости».
Надо узнать кто из участников игры выиграл, если:
- первый игрок получил 5 штрафных и еще 7 штрафных очков;
- второй игрок получил 3 очка и 3 штрафных очков;
- третий игрок получил 4 штрафных очка и 5 очков;
- четвертый игрок получил 9 очков и 11 штрафных очков?
Решение: 1. -5 + (- 7) = - 12 (первый игрок)
2. 3 + (- 3) = 0 (второй игрок)
3. (- 4) + 5 = 1 (третий игрок)
4. 9 + (- 11) = -2 (четвертый игрок)
Ответ: третий игрок выиграл.
Вычислить устно:
3 + (- 2) = - 5 + 4 =
- 4 + (-1) = 4,5 + (- 3) =
2 + (- 2) = 0 + (- 7) =
- 6,5 + 2 = - 8,2 + 0 =
- Какие можно сделать выводы?
(выводы - правила сложения чисел с разными знаками, учащиеся должны сделать самостоятельно)
- при сложении двух отрицательных чисел складываем модули и перед полученным числом ставим знак «минус»;
- при сложении противоположных чисел получается нуль.
- при сложении двух чисел с разными знаками из большего модуля вычитаем меньший, и перед полученным числом, ставим знак того числа, модуль которого больше.
В тетради выполняем №1050(а,в,ж,з,и,л,о,п)
(проверяем: слайд №12 )
Самостоятельная работа.
Вариант 1. Вариант 2.
1. - 32,7 + (- 11,4) = 1. - 5,9 + (- 6,2) =
2. - 2,3 + 4,5 = 2. 2,3 + (- 4,5) =
3. 6,3 + (- 6,3) = 3. -5,4 + 5,4 =
4. 7,5 + (- 9,3) = 4. 6,3 + (- 2,9) =
5. 0 + (- 4,1) = 5. -4,5 + 0 =
6.* -4,3 + 5,8 + (- 6,4) = 6.* - 4,5 + (- 7,3) + 11,8 =
Выполняется взаимопроверка (слайд №14) . Оценки выставляют друг другу карандашом, затем работы сдаются учителю.
Запишем домашнее задание: п. 33 (правила выучить), №885(а),
№1065 (а,б,е,ж,з,л,п), №1069.
(Математика: учебник для 6 класса общеобразовательных учреждений/ Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. - М.:Мнемозина, 2003.)
Итог урока:
Какие правила мы с вами вывели на этом уроке?
Как сложить два отрицательных числа?
Как сложить два противоположных числа?
Как сложить числа с разными знаками?