Контрольная работа по геометрии на тему Площадь. Теорема Пифагора (8 класс)

</ Контрольная работа по теме «Площадь. Теорема Пифагора»

Вариант 1.

1. Какое из утверждений верно?

1. Площадь трапеции равна произведению основания трапеции на высоту.

2. Площадь ромба равна произведению его стороны на высоту, проведенной к этой стороне.

3. В прямоугольном треугольнике гипотенуза равна сумме его катетов.

2. Два катета прямоугольного треугольника равны 3 и 22 . Найдите его площадь.

3. В равнобедренной трапеции основания равны 3 и 7, а один и углов между боковой стороной и основанием равен 45⁰. Найдите площадь трапеции.

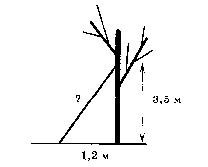
4. Какова длина лестницы ( в метрах), которую прислонили к дереву, если верхний ее конец находится на высоте 3,5 м над землей, а нижний отстоит от ствола дерева на1,2 м?

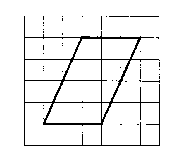
5. На клетчатой бумаге с размером клетки 1* 1 изображен параллелограмм. Найдите его площадь.

6. Сторона ромба равна 9, а расстояние от точки пересечения диагоналей ромба до нее равно 1. Найдите площадь ромба.

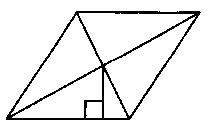
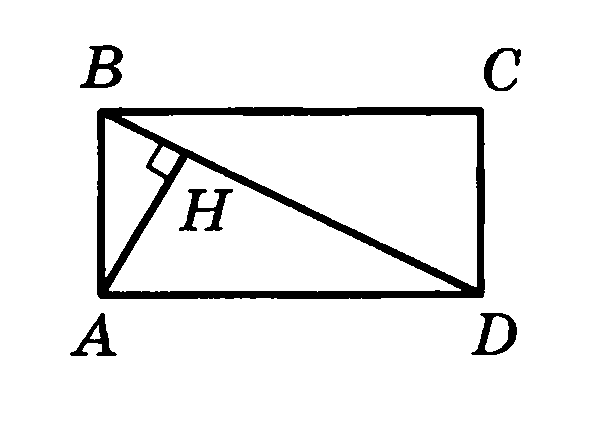
7. На рисунке ABCD- прямоугольник, AH перпендикуляр к BD, сторона АВ в 3 раза меньше стороны ВС. Найдите AH, если BD = 20.

«3» 3-5, «4» 6, «5» -7

Вариант 2.

1. Какое из утверждений верно?

1. Площадь любого параллелограмма равна произведению длин его сторон.

2. Площадь трапеции равна произведению полусуммы оснований на высоту.

3. Площадь треугольника равна произведению его основания на высоту.

2. Два катета прямоугольного треугольника равны 7 и 12 . Найдите его площадь.

3. В равнобедренной трапеции основания равны 3 и 5, а один и углов между боковой стороной и основанием равен 45⁰. Найдите площадь трапеции.

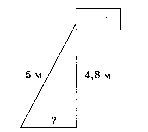
4. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 4,8 м от земли. Длина троса равна 5 м. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.

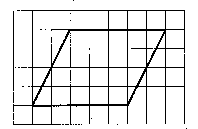
5. На клетчатой бумаге с размером клетки 1 1 изображен параллелограмм. Найдите его площадь.

6. Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до нее равно 4. Найдите площадь ромба.

7. На рисунке ABCD- прямоугольник, СH перпендикуляр к BD, сторона АВ в 3 раза меньше диагонали. Найдите СH, если BС= 20.