Методическая разработка урока алгебры и начала анализа для учащихся 12 классов

по теме: « Способы решения показательных уравнений»

Цели урока

Образовательные:

• Сформировать умения и навыки решения показательных уравнений различными способами:

• Приведение обе части уравнения к одному и тому же основанию;

• Вынесение общего множителя за скобки;

• Приведение к квадратному уравнению;

Развивающие:

• • развитие умения сравнивать, обобщать, правильно формулировать и излагать мысли;

  • развитие навыков реализации теоретических знаний в практической деятельности;

  • развитие интереса к предмету через содержание учебного материала и применение современных технологий.

• Воспитательные:

  • воспитание навыков самоконтроля и взаимоконтроля;

  • воспитание культуры общения, умения работать в коллективе, взаимопомощи;

  • воспитание качеств характера таких как, настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.

Учебно-методическое обеспечение урока.

1. А. Г. Мордкович «Алгебра и начала анализа, 10-11кл. » Мнемозина , 2012 г.

2. Тестовые задания.

3. Мультимедийная презентация

Оборудование: проектор, ПК

Тип урока: изучения нового материала

Методы урока: словесные, наглядные, практические.

Технологии, используемые на уроке:

● технология дифференцированного и разно-уровневого обучения;

● технология обучения в сотрудничестве, индивидуально-групповая технология.

Структура урока:

1. Организационный момент. Мотивационная беседа с последующей постановкой цели урока.(2мин.)

2. Актуализация опорных знаний. Подготовка учащихся к активному и сознательному усвоению нового материала. Математический диктант. (10 мин).

3. Изучение нового материала - рассматриваются способы решения показательных уравнений:

• Приведение обе части уравнения к одному и тому же основанию;

• Вынесение общего множителя за скобки;

• Приведение к квадратному уравнению; (20мин.)

4. Обучающая самостоятельная работа.(12мин)

5. Домашнее задание Подведение итогов урока.(1мин.)

Ход урока.

1.Организационный момент. Мотивационная беседа с последующей постановкой цели урока. Организация внимания.

2 . Актуализация опорных знаний. Подготовка учащихся к активному и сознательному усвоению нового материала.

Вопросы учащимся:

• Какую тему мы изучали на прошлом уроке?

• Какие уравнения называются показательными?

• При каких значениях b, уравнение не имеет решения. Почему?

3.Выполнение математического диктанта с последующей самопроверкой. Ответы на математический диктант проектируются на экран.

1.Решить уравнения:

2.Выписать

показательную функцию

3.Указать возрастающую функцию

1)

4. Изучение нового материала.

5. На доске записаны уравнения. Среди данных уравнений найдите те, которые по каким либо общим внешним признакам похожи друг на друга. ( Слайд 5)

6. Запишите уравнения по этим общим признакам в отдельные столбики

7. 1.

8. 2.

9. 3.

11. 5.

13. 7.

14. 8. 4-x =3^x

16. Учащиеся записывают уравнения в столбики (Слайд 6)

17. 1,5;

18. 2,6,7;

19. 3,4;

20. 8

21. Итак, мы распределили показательные уравнения по схожим признакам и теперь рассмотрим решение данных показательных уравнений.

23. I.УРАВНИВАНИЕ ОСНОВАНИЙ (Слайд 7)

24. Показательное уравнение

27. Рассмотрим решение показательных уравнений:

36. II. ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ (Слайд №8)

38. Используя свойство, преобразуем данное уравнение к виду

44. Следующее уравнение выполняется у доски

45. III. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОЙ ПЕРЕМЕННОЙ (Слайд№9)

46. Решим уравнение.

48. Сделаем замену переменной t = 3^x , Заметим, что 9^x =(3^x)²= t²

49. Поэтому данное уравнение принимает вид:

51. Найдем корни уравнения:

52. и

53. - посторонний корень

54. Откуда получаем

57. Ответ.2

58. IV ГРАФИЧЕСКИЙ МЕТОД

59. Решите уравнение:

60. 4-x =3^x

61. Обе части уравнения представляем в виде функций

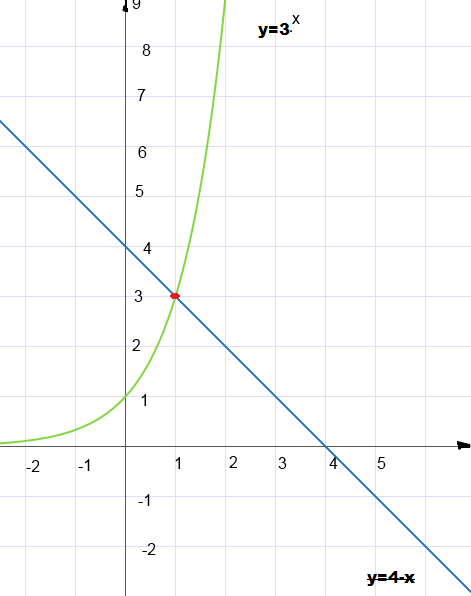
62. y = 4 - x, y = 3^x,

63. Строим графики обоих функций в одной системе координат.

64. Графиком показательной функции

65. y = 3^x является экспонента,

66. Графиком функции y = 4 - x является прямая.

67. Графики пересекаются в одной точке, судя по рисунку в точке ( 1; 3).

68. 

69. Абсцисса этой точки служит решением этого уравнения, значит корень x = 1.

70. Ответ: x = 1.

72. Задания обучающимся: Сформулируйте алгоритмы решения показательных уравнений.

73. 1.Представить обе части показательного уравнения в виде степеней с одинаковыми основаниями;

74. 2.На основании теоремы,

75. если a ^{f (x)}= a ^{g (x)}, где а > 0, a 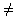1 равносильно уравнению f(x) = g(x), приравниваем показатели степеней.

76. 3.Решаем полученное уравнение, согласно его вида (линейное, квадратное и т. д.).

77. Записываем ответ.

    106. 1.Определить возможность переписать данное уравнение в новом виде, позволяющем ввести новую переменную.

    107. 2.Вводим новую переменную и

    108. решаем уравнение относительно новой переменной.

    109. 3. Относительно найденных значений новой переменной переходим к простейшим показательным уравнениями решаем его.

    110. 4.Записываем ответ.

    111. 1.Левую и правую части уравнения представить в виде функций.

    112. 2.Построить графики обоих функций в одной системе координат.

    113. 3.Найти точки пересечения графиков, если они есть.

    114. 4. Указать абсциссы точек пересечения графиков -это и есть корни уравнения.

79. 5. Проверка понимания учащимися изученного материала.

80. Учащиеся оценивают свои возможности и уровень усвоения новой темы.

81. По результатам оценивания, обучающие сами выбирают вариант самостоятельной работы

83. 131. 

84. Работа проходит индивидуально. При возникновении затруднений учащиеся обращаются за консультацией к учителю.

85. 5 этап: Рефлексия. Подведение итогов урока. Домашнее задание

86. №1358(а,в) №1361 (б) №1365(б,г) №1366(а,в) №1367(а)

88. Опросный листактивно

89. пассивно

    151. 2

    152. Своей работой на уроке я

    • доволен

    • не доволен

    153. 3

    154. Урок для меня показался

    • коротким

    • длинным

    155. 4

    156. За урок я

    • не устал

    • устал

    157. 5

    158. Моё настроение

    • стало лучше

    • стало хуже

    159. 6

    160. Материал урока мне был

    • понятен

    • не понятен

    • полезен

    • бесполезен

    • интересен

    • скучен

90. Урок закончен. Спасибо за урок!