- Учителю
- Программа курса по выбору «Школа математиков», 5 класс
Программа курса по выбору «Школа математиков», 5 класс








































































 «Теміртау қаласының білім беру, дене шынықтыру және спорт бөлімі» ММ
«Теміртау қаласының білім беру, дене шынықтыру және спорт бөлімі» ММ
ГУ «Отдел образования, физической культуры и спорта города Темиртау»
«Теміртау қаласының №27 жалпы білім беретін орта мектебі» КММ
КГУ «Общеобразовательная средняя школа №27 города Темиртау»
Программа утверждена: на заседании МС 15. 11. 2011 г
ПРОГРАММА КУРСА ПО ВЫБОРУ
« Школа математиков»
5 класс
Автор программы: Слаткова Оксана Михайловна,
учитель математики ОСШ №27
Темиртау - 2011
Пояснительная записка
Непрерывно возрастают роль и значение математики в современной жизни. Но, к сожалению, интерес к изучению математики заметно падает. А ведь еще в древности одним из важнейших достоинств человека считали владение математическими знаниями.
Настоящая программа предназначена для работы с одаренными детьми - для подготовки учащихся 5 классов к различным интеллектуальным конкурсам, соревнованиям и олимпиадам по математике. Является частью сквозной программы «Школа математиков» для учащихся 5-11 классов, которая позволяет организовать систематическую работу при подготовке олимпийского резерва. Курс предусматривает не только овладение различными умениями, навыками, приёмами для решения задач, но и создаёт условия для формирования мировоззрения ученика, логической и эвристической составляющих мышления. Программа курса рассчитана на 34 часа в пятом классе.
Данная программа состоит из трех глав посвященных решению задач по темам: «Числа», «Упражнения со спичками», и «Текстовые задачи».
Для реализации целей и задач данного курса предполагается использовать следующие формы занятий: лекции, практикумы по решению задач, различные конкурсы и игры. При изучении курса используются интерактивные формы работы: работа в малых группах, тренинг, тестирование. Доминантной же формой учения должна стать исследовательская деятельность ученика, которая может быть реализована как на занятиях в классе, так и в ходе самостоятельной работы учащихся. Ученик лучше поймет материал, его знания будут более прочными, если они будут закреплены в результате исследовательской деятельности ученика.
Все занятия должны носить проблемный характер, что способствует успешному усвоению курса. Контроль за знаниями учащихся планируется провести в виде различных интеллектуальных конкурсов и марафонов, проводимых по окончанию изучения каждого раздела.
Изучение математики осуществляется в основном в процессе решения задач. Решение задач выступает и как цель, и как средство обучения. Умение решать задачи является одним из основных критериев уровня математического развития обучающихся. В ходе работы над задачами формируется творческое мышление. Поэтому целью предлагаемого курса является повышение интереса к математике и развитие математических способностей школьников, с помощью решения не стандартных занимательных задач.
Цель: Создать условия для повышения математической компетентности и развития коммуникативной компетенции.
Задачи:
-
Создать условия для формирования представлений учащихся о быстром счете, вычислении возраста, дележе при затруднительных обстоятельствах, работе с часами, фигурах, числах из спичек;
-
создать условия для формирования и развития практических умений учащихся решать различные задачи на делимость натуральных чисел, передвижения, переправы и разъезды, переливания, фальшивые монеты, расположения, перекладывания;
-
развивать интеллектуальные способности учащихся, формировать качества мышления, характерные для математической деятельности и необходимые человеку для полноценной жизни в обществе, развивать мыслительные способности учащихся: умения анализировать, сопоставлять, сравнивать, систематизировать и обобщать;
-
воспитывать у учащихся самостоятельность, умение определять уровень усвоения учебного материала, а также способность к самоорганизации.
5. Содействовать формированию у учащихся навыков развития
познавательных процессов и коммуникативной компетенций.
В результате изучения данного курса учащиеся:
должны знать:
- производить в уме арифметические действия в пределах сложности примеров на сложение и вычитание двузначных чисел, умножение и деление нацело двузначного числа на однозначное;
- уверенно выполнять сложение, вычитание, умножение и деление натуральных чисел, в записи которых имеется несколько десятичных разрядов (включая сложные случаи переноса из разряда в разряд и использование нулей в записи числа);
- выполнять арифметические действия над обыкновенными дробями (включая обращение смешанного числа в обыкновенную дробь, нахождение общего знаменателя дробей, сокращение дробей и представление их в виде смешанных чисел;
- выполнять арифметические действия над десятичными дробями, производить округление десятичных дробей;
- вычислять значения числовых выражений, включающих в себя целые числа, обыкновенные и десятичные дроби; производить вычисления по формулам;
- составлять числовые и буквенные выражения, пропорции и линейные уравнения по условиям текстовых задач;
- решать линейные уравнения, используя при этом раскрытие скобок и приведение подобных слагаемых;
- решать текстовые задачи с помощью арифметических приемов (включая основные задачи на дроби и на проценты) и уравнений;
- распознавать и изображать геометрические фигуры;
- производить простейшие измерения при помощи линейки, угольника, транспортира, циркуля.
Ожидаемые результаты: 1) повышение уровня математической грамотности учащихся;
2) повышение уровня коммуникативной компетентности учащихся;
Диагностический инструментарий:
1) анкеты на «входе», «выходе»;
2) практические и творческие работы учащихся;
3) рефераты и проекты;
4) тесты по Беспалько.
.
Ожидаемые результаты:
-
сформированность практических умений, информационных навыков и компетенций по данной теме;
-
развитость социально-коммуникативных компетенций у учащихся;
-
умение представлять результат своей деятельности, проводить самоанализ деятельности и самооценку её результата.
Методы и формы обучения:
-
тестовый метод;
-
исследовательский метод;
-
проблемно-поисковый.
Формы организации учебной работы:
-
индивидуально-групповые;
-
групповые;
-
моделирование.
Формы проведения занятий:
-
лекция-диалог;
-
тренинг-лекция
-
индивидуальная работа;
-
практикум;
-
игра;
-
соревнование.
Учебно-тематический план.
№
Темы или разделы
Количество часов
Формы и методы обучения
Образовательный продукт
Примечания
1
Арифметические действия над натуральными числами и нулем и их свойства.
2 часа
Атака мыслей
Анкета, записи
2.
Делимость натуральных чисел.
2 часа
Мини- лекция, тренинг с применением ПК, практикум,деловая игра
Опорный конспект, решенные задания,
продуктивный реферат
3.
Задачи с использованием НОД и НОК.
1 час
Исследовательская работа с применением ПК, тренинг, семинар-практикум,метод проектов
Распечатка построенных графиков, памятка с алгоритмами и правилами, опорные конспекты,мини-проекты
4.
Задачи и ребусы.
2 часа
Практикум, тренинг с применением ПК, мини-лекция,деловая игра, проектирование
Конспект, памятка, реферат, решенные задания,проекты
5.
Быстрый счет.
2 часа
Мини-лекция, семинар, практикум,
проектирование
Конспект, алгоритмы решений, опорные схемы, решенные задания,проекты
6.
Сказки и старинные истории.
1 час
Практикум,
Схемы решений, решенные задания
7.
Как сосчитать.
1 час
Тестирование, защита проектов
Результаты теста, проект, продуктивный реферат
8.
Передвижения.
2 часа
лекция с обратной связью,
исследование,
семинар
конспект
исследование
решённые задания
9.
Вычисление возраста.
1 час
работа в группах
практикум
проектирование
конспект
схемы решений
решённые задания
10.
Часы.
1 час
лекция с обратной
связью,
тестирование,
конспект,
результаты тестов
репродуктивный реферат, проект
11.
Дележи при затруднительных обстоятельствах.
1 час
Атака мыслей
записи
12.
Фигуры из спичек.
1 час
Мини- лекция, тренинг с применением ПК, практикум,деловая игра
Опорный конспект, решенные задания,
продуктивный реферат
13.
Числа из спичек.
1 час
Исследовательская работа с применением ПК, тренинг, семинар-практикум,метод проектов
памятка с алгоритмами и правилами, опорные конспекты,мини-проекты
14.
Равенства из спичек.
1 час
Практикум, тренинг с применением ПК, мини-лекция,деловая игра, проектирование
Конспект, памятка, реферат, решенные задания,проекты
15.
Игры со спичками.
1 час
Практикум
Конспект, решенные задания,
проекты
16.
Переправы и разъезды.
2 часа
Мини-лекция, семинар, практикум,
Схемы решений, решенные задания
17.
Переливания.
2 часа
Тестирование, защита проектов
Результаты теста, продуктивный реферат
18.
Фальшивые монеты.
2 часа
Атака мыслей
записи
19.
Расположения.
1 час
Мини- лекция, тренинг с применением ПК, практикум,деловая игра
Опорный конспект, решенные задания,
20.
Перекладывания.
1 час
Исследовательская работа с тренинг, метод проектов
21.
Маленькие хитрости.
2 часа
Практикум, тренинг с применением ПК, мини-лекция,деловая игра,
Конспект, памятка, реферат, решенные задания,проекты
22.
Логические задачи.
4 часа
Тестирование, защита проектов
Результаты теста, проект, продуктивный реферат Тестирование, защита проектов
Содержание курса:
Глава «Числа» содержит 16 часов решения задач, связанных с арифметическими действиями над натуральными числами, нулем и их свойствами, рассматривает задачи-ребусы, задачи на применение быстрого счета, сказки и старинные истории, задачи на передвижение, на вычисление возраста, на дележи при затруднительных обстоятельствах и другие.
Вторая глава содержит материал для упражнений со спичками - составление фигур, чисел, равенств и игр (4 часа).
В третьей главе рассматривается решение текстовых задач на переправы и разъезды, переливания, фальшивые монеты, перекладывания, расположения и знакомству с маленькими математическими хитростями (14 часов).
Темы продуктивных рефератов:
-
Числа- великаны и числа - малютки.
-
Как люди научились считать .
3. История календаря.
Темы проектов:1. Магические квадраты.
2. Частные случаи числа.
3. Как НОК и НОД чисел помогает решать интересные и
разнообразные задачи.
4.Творческие задания для учащихся 5 классов на уроках
математики.
Список литературы
Список литературы для учителя:
1. П.Р. Оникул. 19 игр по математике. С,- Петербург: Союз,1999.
-
А.В. Фарков Математические кружки в школе 5-8 классы: Методическое пособие для подготовки и проведения занятий школьного математического кружка. - Москва: «АЙРИС - ПРЕСС», 2005.
-
В.И. Арнольд Задачи для детей от 5 до 15 лет. Сборник задач для развития культуры мышления. -Астана: «Дарын», 2008.
4. А.В. Шевкин. Школьная олимпиада по математике. Задачи и решения.
- Москва: « Русское слово», 2004.
5. Ю.Нестеренко, С. Олехник, М.Потапов. Лучшие задачи на смекалку. Москва: АСТ - ПРЕСС,1999.
6. Л.М. Худодатова. Математика в ребусах, кроссвордах, чайнвордах, криптограммах, 5 класс. - Москва: Школьная Пресса, 2002.
7. Республиканский НПЦ «Дарын». Задачи I Республиканского математического турнира младших школьников «Бастау» (15-18 июня 2008г.) - Астана, 2009.
8. Н.П. Кострикина. Задачи повышенной трудности в курсе математики 4-5 класса. Книга для учителя. - Москва, «Просвещение», 1986.
Список литературы для учащихся:
-
Я.И Перельман Занимательная алгебра. Книга для вольного чтения.- Москва: 1975.
2. Энциклопедия головоломок: Книга для детей и родителей. - Москва: АСТ - ПРЕСС,1999.
3. Д.В. Клименченко. Задачи по математике для любознательных.
-Москва: «Просвещение» 1992.
4. В.А. Крутецкая. Математика 5-8 классы. Доклады, рефераты, сообщения.- СПб.: Издательский дом «Литера», 2007.
5. Н.В. Удальцова. Математические шарады и ребусы. Библиотечка «Первого сентября» Серия «Математика». Выпуск 35. - Москва: «Чистые пруды», 2010.
6. И.Н. Сергеев, С.Н. Олехник, С.Б. Гашков. Примени математику. Для школьников и всех любителей математики. - Москва: «Наука», 1989.
7. Ю.М. Колягин. Учись решать задачи. Книга для детей и родителей. - Москва: «Просвещение», 1980.
Учебно-методический комплекс курса
Приложение 1
Приложение 1.1
Арифметические действия над натуральными числами, нулем и их свойства
Сладкая черешня
В овощной магазин 141 кг черешни в ящиках по 10 кг и по 13 кг.
Сколько было привезено ящиков?
Решение.
Пусть в тринадцатикилограммовых ящиках а кг черешни, а в десятикилограммовых - b кг.
Числа а и b - натуральные. Тогда число b делится на 10, т.е. оканчивается цифрой 0, и, следовательно, число а оканчивается цифрой 1, а значит, количество тринадцатикилограммовых ящиков оканчивается цифрой 7, но 13 · 17 = 221, 221 > 141, т.к. 13 · 7 = 91, 91 < 141.
Таким образом, было 7 тринадцатикилограммовых и 5 десятикилограммовых ящиков, т.к. 141 - 91 = 50.
Ответ: 7 ящиков по 13 кг и 5 ящиков по 10 кг.
На ферме
На ферме выращивают кроликов и фазанов. В настоящее время их столько, что вместе 740 голов и 1980 ног.
Сколько же в настоящее время находится на ферме кроликов и фазанов?
Решение.
Пусть х - число фазанов, у - число кроликов.
Тогда 2х + 4у = 1980 и
х + у = 740,
откуда х = 490, у = 250.
Ответ. На ферме имеется 490 фазанов и 250 кроликов.
Числа из таблицы
1
1
1
3
3
3
5
5
5
7
7
7
Можно ли выбрать из таблицы 5 чисел, сумма которых равна 20?
Решение: Все числа в таблице - нечетные, а сумма пяти нечетных чисел - число нечетное и поэтому равняться 20 не может.
Ответ. Нельзя.
Змей Горыныч
У Змея Горыныча 2000 голов. Сказочный богатырь одним ударом отрубает 1, 17, 21 или 33 головы, но при этом, соответственно вырастают 10, 14, 0 или 48 голов. Если все головы отрублены, то новые не отрастают.
Сможет ли богатырь победить Змея Горыныча?
Решение.
Можно предложить следующую тактику отрубания голов у змея Горыныча:
1) вначале будем отрубать по 21 голове (94 раза), новых голов не отрастает, и у Змея останется 26 голов;
2) далее отрубим три раза по 17 голов (напомним, что при этом вырастает по 14 голов) - после чего останется отрубить 17 голов;
3) последним ударом отрубим 17 голов.
(2000 - 21 · 94) - 3 · (17 - 14) - 17 = 0.
Ответ. Богатырь сможет победить Змея Горыныча.
Кузнечик
Кузнечик прыгает по прямой: первый прыжок на 1 см, второй - на 2 см, третий - на 3 см и так далее. Может ли он после двадцать пятого прыжка вернуться в ту точку, с которой начал?
Решение.
Пусть кузнечик прыгает по числовой прямой и начинает из точки с координатой 0. После 25 прыжка он окажется в точке с нечетной координатой (среди чисел от 1 до 25 - нечетных - нечетное число). Так как 0 - число четное, то он не может вернуться.
Ответ: После двадцать пятого прыжка кузнечик не может вернуться в ту точку, с которой начал.
Тайна древней рукописи
В древней рукописи приведено описание города, расположенного на 8 островах. Острова соединены между собой и с материком мостами. На материк выходят 5 мостов; на 4 островах берут начало по 4 моста, на 3 островах берут начало по 3 моста и на один остров можно пройти только по одному мосту.
Может ли быть такое расположение мостов?
Решение.
Найдем число концов у всех мостов:
5 + 4 · 4 + 3 · 3 + 1 = 31.
31 - является числом нечетным.
Так как число концов у всех мостов должно быть четным, то такого расположения мостов быть не может.
Ответ: Такого расположения мостов быть не может.
Приложение 1.2
Делимость натуральных чисел
Для тренировки
Среди четырех утверждений:
"число а делится на 2", "число а делится на 4", "число а делится на 12", "число а делится на 24" - три верных, а одно неверное.
Какое?
Ответ.
Заметим, что "число а делится на 24" ⇒ "число а делится на 12" ⇒ "число а делится на 4" ⇒ "число а делится на 2". Следовательно, неверным может быть только утверждение "число а делится на 24".
Счастливые билеты
Автобусные билеты имеют номера от 000001 до 999999. Билет называется счастливым, если у него сумма первых трех цифр равна сумме трех последних.
Докажите, что сумма номеров всех счастливых билетов делится на 9, 13, 37 и 1001.
Доказательство.Счастливому билету с номером а1а2а3а4а5а6 соответствует единственный счастливый билет с номером b1b2b3b4b5b6, такой что
а1 + b1 = 9;
а2 + b2 = 9;
…
а6 + b6 = 9.
Следовательно, сумма всех номеров счастливых билетов делится на 999999, а значит и на 9, 13, 37 и 1001.
Ч.т.д.
На диком Западе
Ковбой Джо зашел в бар. Он купил бутылку виски за 3 доллара, трубку за 6 долларов три пачки табака и девять коробок непромокаемых спичек. Бармен сказал: "С вас 11 долларов 80 центов за все". Вместо ответа Джо выхватил револьвер.
Почему он решил, что бармен собирается его надуть?
Ответ: Из условия следует, что общая стоимость всей покупки должна делиться на 3, а 11,8 долларов на 3 не делится.
Случай в сберкассе
Можно ли разменять 25 рублей при помощи десяти купюр достоинством 1, 3 и 5 рублей?
Ответ: Нельзя. И вовсе не потому, что таких купюр не существует. Сумма четного количества нечетных слагаемых не может быть нечетным числом.
Потерянная гиря
В наборе было 23 гири массой 1 кг, 2 кг, 3 кг, …23 кг.
Можно ли их разложить на две равные части по массе кучки, если гирю в 21 кг потеряли?
Решение.
Число S = (1 + 23) + (2 + 22) + … + (11 + 13) + 12 - четное.
Следовательно, (S - 21) на две равные по весу кучки не разложить.
Ответ: Нельзя разложить гири массой 1 кг, 2 кг, 3 кг, …23 кг на две равные части по массе кучки, если гирю в 21 кг потеряли.
Приложение 1.3
Задачи с использованием НОД и НОК
Найди остаток
При делении на 2 число дает остаток 1, а при делении на 3 - остаток 2.
Какой остаток дает это число при делении на 6?
Решение.
Так как при делении целого числа на 6 можно получить один из остатков: 0, 1, 2, 3, 4 и 5, то множество целых неотрицательных чисел можно разбить на непересекающиеся подмножества чисел вида 6k, 6k + 1, 6k + 2,
6у + 3, 6k + 4 и 6у + 5, где k = 0, 1, 2, 3, … .
Так как при делении на 2 данное число дает остаток 1, то оно нечетное, поэтому остается рассмотреть числа вида 6k + 1, 6у + 3 и 6у + 5.
Числа вида 6k + 1 при делении на 3 дают остаток 1, числа вида 6k + 3 кратны 3 и только числа вида 6k + 5 при делении на 3 дают остаток 2.
Следовательно, число имеет вид 6у + 5, т.е. при делении на 6 дает остаток 5.
Ответ.
Если при делении на 2 число дает остаток 1, а при делении на 3 - остаток 2, то при делении на 6 число остаток 5.
Приложение 1.4
Задачи и ребусы
I. Устная работа
-
Вы - шофер автобуса. В автобусе первоначально было 23 пассажира. На первой остановке вышло 3 женщины и зашло 5 мужчин. На второй остановке зашло 4 мужчины и вышло 7 женщин. Сколько лет шофёру?
-
Продавая в магазине попугая, продавец пообещал, что попугай будет повторять каждое услышанное им слово. Покупатель очень обрадовался, но, придя домой, обнаружил, что попугай «нем как рыба». Тем не менее, продавец не лгал. Как это могло быть?
-
Петя решил купить Маше мороженое, но для его покупки ему не хватило 30 т, а Маше всего лишь 10 т. Тогда они решили сложить свои деньги, но опять не хватило 10 т на покупку даже одного мороженого. Сколько стоила порция мороженого? Сколько денег было у Пети?
-
Изучение нового материала
-
Я задумал число, умножил его на два, прибавил три и получил 17. Какое число я задумал?
-
Однажды черт предложил бездельнику заработать. «Как только ты перейдешь через этот мост, - сказал он, - твои деньги удвоятся. Можешь переходить по нему сколько хочешь раз, но после каждого перехода отдавай мне за это 24 т». Бездельник согласился и … после третьего перехода остался без гроша. Сколько денег у него было сначала?
-
Трое мальчиков имеют по некоторому количеству яблок. Первый мальчик дает другим столько яблок, сколько каждый из них имеет. Затем второй мальчик дает двум другим столько яблок, сколько каждый из них теперь имеет; в свою очередь и третий дает каждому из двух других столько, сколько есть у каждого в этот момент. После этого у каждого из мальчиков, оказывается, по 8 яблок. Сколько яблок было у каждого мальчика в начале?
-
Решите ребусы: а) * * б) * * в) Д Р А М А
* * * Д Р А М А
* * 8 * 9 8 Т Е А Т Р
III. Домашнее задание
-
Над озерами летели гуси. На каждом озере садилась половина гусей и ещё полгуся, остальные летели дальше. Все сели на семи озерах. Сколько было гусей?
( Половинка гуся сесть не может, следовательно, на каждом озере садилось целое число гусей.)
-
Решите ребус: К О К А
К О Л А
В О Д А
Ребусы
Ответ: два
Ответ: диагональ Ответ: диаметр
Ответ: дробь
МУДРЫЕ МЫСЛИ
"Человек подобен дроби: в знаменателе - то, что он о себе думает, в числителе - то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь".
Лев Толстой
Ответ: числитель
Ответ: задача.
Ответ: линейка
Ответ: минус
Ответ: отрезок
Ответ: степень
МУДРЫЕ МЫСЛИ
"Знание - самое превосходное из владений. Все стремятся к нему, само же оно не приходит".
Аль-Бируни
Числовые ребусы
Требуется расшифровать запись арифметического равенства, в котором цифры заменены буквами, причем разные цифры заменены разными буквами, одинаковые - одинаковыми. Предполагается, что исходное равенство верно и записано по обычным правилам арифметики. В частности, в записи числа первая слева цифра не является цифрой 0; используется десятичная система счисления.
Сложение
№1. Животноводческий ребус
Б + Б Е Е Е = М У У У
Решение: Так как при сложении данных чисел цифра Е в разряде десятков поменялась на цифру У, то суммой однозначных чисел Б и Е является двузначное число, начинающееся с единицы. Так как помимо увеличения на единицу цифры в разряде десятков также изменилась и цифра в разряде сотен, то Е = 9, Б = 1, У = 0.
Ответ: 1 + 1999 = 2000.
№2. Кока-Кола
+
К
О
К
А
К
О
Л
А
В
О
Д
А
№3. Драма
+
У
Д
А
Р
У
Д
А
Р
Д
Р
А
М
А
№4. Кросс
+
С
П
О
Р
Т
С
П
О
Р
Т
К
Р
О
С
С
№5. Собаки
+
Б
А
Р
Б
О
С
Б
О
Б
И
К
С
О
Б
А
К
И
№6. Дружба
+
А
Н
Д
Р
Е
Й
Ж
А
Н
Н
А
Д
Р
У
Ж
Б
А
№7. Молоко
Докажите, что у ребуса нет ни одной расшифровки.
+
К
О
Р
О
В
А
Т
Р
А
В
А
М
О
Л
О
К
О
№8. Удача
+
Т
Р
У
Д
В
О
Л
Я
У
Д
А
Ч
А
Дополнительное условие: числа ТР и ВО делятся на 13.
№9. Реши, если силен
+
Р
Е
Ш
И
Е
С
Л
И
С
И
Л
Е
Н
№10. Класс
+
С
Т
О
Л
С
Т
У
Л
К
Л
А
С
С
№11. Коля и Оля
К + О + Л + Я = О Л - Я
Расшифруйте при дополнительном условии: К + О + Л + Я = 21.
Расшифруйте без этого дополнительного условия (более 10 ответов).
Приложение 1.5
Быстрый счет
Для того чтобы быстро и уверенно считать в уме, не нужно иметь ни специальных знаний, ни способностей. Несколько простых правил, а главное - постоянная тренировка в устном счете, помогут научиться хорошо, считать. Бывают люди, которые быстро множат и делят в уме четырех и пятизначные числа. Достичь такого искусства трудно, надо помнить много правил, очень долго и утомительно тренироваться. Это искусство в практической жизни почти не может пригодиться. Наша задача - научиться работать с двузначными, иногда - с трехзначными числами. Этого для экономии времени на уроке достаточно.
Сложение (слайд 2, 3).
Складывать в уме очень легко; и все-таки о сложении нужно сказать несколько слов. Ведь сложение основное действие, поэтому складывать надо очень быстро и уверенно.
-
И так, однозначное слагаемое представляем в виде суммы двух меньших чисел, из которых одно дополняет большее слагаемое до целых десятков. Самая небольшая тренировка приводит к тому, что это разложение выполняется совершенно автоматически, без всякого усилия воли или внимания.
-
Если оба слагаемых многозначные числа, то к большему прибавляем сначала старший разряд меньшего, потом - младший разряд. Так, если прибавляется двузначное число, то сначала прибавляют десятки, потом единицы.
-
При сложении нескольких двузначных чисел складываем сначала все десятки, потом все единицы и к общему числу десятков прибавляем единицы
Вычитание (слайд 4, 5)
-
Если нужно вычесть однозначное число, большее последней цифры уменьшаемого, то разбиваем это однозначное число на два (равное последней цифре уменьшаемого и остаток) и вычитаем полученное число одно за другим.
-
При вычитании двузначных (и многозначных) чисел сначала отнимаем старшие разряды вычитаемого, потом младшие его разряды.
-
Если вычитаемое близко к круглому числу, то сначала отнимаем это круглое число, а затем делаем поправку.
Простейшие случаи умножения и деления (слайд 6)
-
Умножать и делить проще всего на 10, 100, вообще на число, изображаемое единицей с нулями. При умножении на такие числа мы приписываем к множимому столько нулей, сколько их имеется в множителе.
-
При делении на число, изображаемое единицей с нулями, отделяем запятой столько последних цифр, сколько имеется нулей в делителе. Ответ чаще всего получается дробный (слайд 8).
-
Просто умножение на 2 и на 4. Умножаем на 2, начиная со старших разрядов (слайд 7).
-
Умножение на 4 сводится к двукратному умножению на 2.
-
При делении пополам делим пополам все разряды, начиная с высшего, попутно складывая получающиеся результаты (слайд 9).
-
При делении на 4 делим сначала на 2, затем полученное частное еще раз на 2.
-
Не нужно удивляться, что ответ получился с дробью. При делении почти всегда так и бывает.
-
Только в редких случаях деление чисел, взятых из практической задачи, приводит к целому числу.
-
Если нужно разделить на 8 или на 16, то будем три или четыре раза последовательно делить на 2.
Умножение и деление на 5, 25, 50 (слайд 10, 11, 12)
-
Умножение на 5 сводится тс делению пополам, деление на 5 - к умножению на 2.
-
При умножении на 25 мы умножаем на 100 и делим на 4. При делении на 25 - умножаем на 4 (т.е. два раза на 2) и делим на 100.
-
При умножении на 50 умножаем на 100 и делим пополам, при делении на 50 сначала удваиваем, потом делим на 100.
-
Увеличение в 1,5 раза. Умножение на 15 (слайд13).
-
Очень легко увеличить некоторое число в 1,5 раза, для этого нужно к самому числу прибавить его половину.
-
Чтобы умножить некоторое число на 15, мы увеличиваем его в 10 раз и к полученному числу прибавляем половину того, что получилось.
Умножение на 9, 11, 99, 101 (слайд 14-17)
-
Чтобы умножить какое-нибудь число на 9, нужно увеличить его в 10 раз и от полученного результата отнять само данное число.
-
Чтобы умножить какое-нибудь число на 11, нужно увеличить его в 10 раз и к полученному результату прибавить само данное число.
-
Возьмем число 87 умножим его на 11. Увеличив 87 в десять раз, получим 870. Прибавим теперь 87 получим 957.
-
Заметим еще один прием умножения двузначного числа на 11. Раздвинем цифры двузначного числа и вставим между ними их сумму. Получим нужный результат. Умножим, например, 24 на 11. Раздвигаем цифры 2 и 4 (2. . .4) и между ними вставляем сумму 2+4=6. Получим 264. Значит, 24*11= 264.
-
Если сумма цифр двузначного числа сама является двузначной, то ее единицы вставляем между цифрами данного числа, а десятки прибавляем к первой цифре. Например, 67 умножаем на 11. Раздвигаем цифры б и 7 (6. ..7) и между ними вставляем 6 + 7= 13. Получим 6 (13) 7. Теперь тройку оставляем на месте, а единицу прибавляем к шести. Получим 737. Значит, 67 11 = 737. При небольшом навыке все это легко делается в уме.
-
Особенно просто умножение двузначного числа на 101. Нужно мысленно приписать справа к данному числу его самого и прочесть то, что получится.
-
Нетрудно сообразить, как поступать при умножении на 99. Нужно, очевидно, увеличить данное число в 100 раз и от полученного числа отнять само данное число.
Умножение на 3 и 6 (слайд 18)
-
При умножении двузначного числа на 3,сначала умножаем десятки, потом единицы, затем оба результата складываем.
-
Умножать на 6. Лучше сначала умножить данное число на 3, а затем результат удвоить.
Используемая литература:
Г.Н.Берман "Приёмы счета". Москва. 1959 г.
Приложение 1.6
Передвижения
Лиса и овчарка
Овчарка погналась за лисой, когда между ними было расстояние 99 м. скачок лисы 1,1 м, скачок овчарки 2,2 м. Когда овчарка делает 19 скачков, лиса делает 29 скачков. Сколько метров проскачут они, пока овчарка догонит лису?
Решение.
Если 19х - количество скачков овчарки, а 29у - количество скачков лисы, то 19 · 2,2х - 29 · 1,1у = 99 или 38х - 29у = 90, откуда наиболее реальные значения х = 10, у = 10.
Если х = 10, тогда 19х = 190 скачков.
Если у = 10, тогда 29у = 290 скачков.
Ответ: Овчарка проскачет 418 м, лиса - 319 м.
Встретились дважды
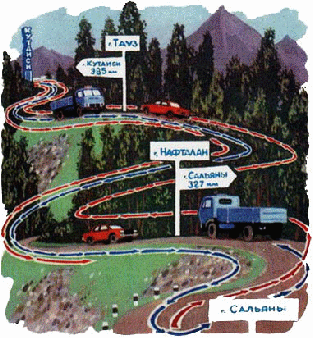
Легковая машина вышла из города Сальяны, направилась в сторону Кутаиси и встретилась с грузовой автомашиной, которая одновременно вышла из Кутаиси в направлении к Сальяны. Встреча произошла на расстоянии 385 км от Кутаиси в город Тауз.
Когда автомашины достигли своих пунктов назначения, они тут же повернули обратно и вторично встретились на расстоянии 327 км от города Сальяны в городе Нафталан.
Найдите расстояние между городами Сальяны и Кутаиси.
Решение.
Пусть х - расстояние между городами Сальяны и Кутаиси, тогда к моменту первой встречи оба автомобиля вместе прошли х км за время t, а к моменту второй встречи прошли вместе 3х км за время 3t.
Так как грузовик за время t прошел 385 км, то за время 3t он прошел 385 × 3 = 1155 (км); 1155 = х + 327, т.е. х = 828.
Ответ: Расстояние между городами Сальяны и Кутаиси 828 км.
Рак-велосипедист
Рак-велосипедист проехал от деревни до города со скоростью 15 км/ч, а возвращается со скоростью 10 км/ч.
Какова средняя скорость рака-велосипедиста?
Решение.
Пусть расстояние от деревни до города - s км. Тогда в город рак-велосипедист доехал за s / 10 ч. Всего велосипедист затратил s / 6 ч:
s / 15 + s / 10 = s / 6.
Следовательно, его средняя скорость равна: 2s : (s / 6) = 12 (км/ч).
Ответ: Средняя скорость рака-велосипедиста 12 км/ч.
Длина и скорость поезда
Поезд проходит мост длиной 450 м за 45 с, а мимо будки стрелочника - за 15 с.
Вычислите длину поезда и его скорость.
Решение.
Замечание.
Фраза "поезд проходит мост за 45 с" означает, что 45 с - это время с момента, когда начало поезда вступит на мост, до момента, когда конец поезда сойдет с моста.
Фраза "мимо будки стрелочника поезд проходит за 15 с" означает, что поезд свою длину мимо любой точки протягивает за 15 с.
I способ
1) 45 - 15 = 30 (с) - время, за которое проходит мост любая точка поезда.
2) 450 : 30 = 15 (м/с) - скорость поезда.
3) 15 × 15 = 225 (м) - длина поезда.
II способ
Пусть скорость поезда х м/с. Тогда длина поезда 15х м. За 45 с поезд проходит расстояние 45х м, или (450 + 15х) м. Получаем уравнение:
45х = 450 + 15х,
откуда
х = 15.
Ответ: Длина поезда 225 м, а его корость 15 м/с.
Буддийский монах
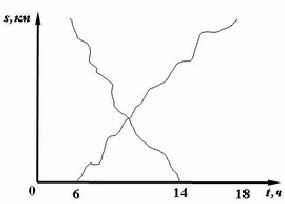
Монах с 6 утра до 6 вечера поднимался на гору и там ночевал, а на следующий день с 6 утра до 2 дня опускался по той же дороге.
Докажите, что в пути было такое место, где он находился в одно и то же время и на подъеме и на спуске (монах часто отдыхал и шел неравномерно).
Решение.
Из графика видно, что такое место обязательно найдется.
Путешествие мушкетеров
Расстояние между Атосом и Арамисом, едущими верхом по дороге, равно 20 лье. За один час Атос проезжает 4 лье, а Арамис - 5 лье. Какое расстояние будет между ними через час?
Решение.
Возможны четыре случая (сделайте рисунок!):
1) мушкетеры едут навстречу друг другу, тогда расстояние между ними через час будет равно 20 - (4 + 5) = 11 (лье);
2) мушкетеры едут в разные стороны, в этом случае:
20 + (4 + 5) = 29 (лье);
3) мушкетеры едут в одну сторону, Арамис догоняет Атос, т.е. 20 + 4 - 5 = 19 (лье);
4) мушкетеры едут в одну сторону, Арамис впереди: 20 + 5 - 4 = 21 (лье).
Ответ: 11 лье; 29 лье; 19 лье; 21 лье.
Бедная" собака
Из двух пунктов, расстояние между которыми 100 км, выехали одновременно навстречу друг другу два всадника. Скорость первого всадника 15 км/ч. Второго - 10 км/ч. Вместе с первым всадником выбежала собака, скорость которой 20 км/ч. Встретив второго всадника, она повернула назад и побежала к первому, добежав до него, снова повернула и так и бегала до тех пор, пока всадники не встретились. Сколько километров пробежала собака?
Решение.1) 10 + 15 = 25 (км/ч) - скорость сближения всадников.
2) 100 : 25 = 4 (ч) - время движения всадников и собаки.
3) 20 × 4 = 80 (км) - расстояние, которое пробежала собака.
Ответ: Собака пробежала 80 км.
Приложение 1.7
Вычисление возраста
Первая мать-героиня
Первый орден "Мать-героиня" был вручен жительнице Пушкинского района московской области Анне Савельевне Алексахиной в 1944 году.
Десять сыновей и двое дочерей было в семье Алексахиной (по старшинству: Сергей, Алексей, Александр, Иван, Георгий, Валентин, Михаил, Николай, Владимир, Андрей, Виктория и Светлана), причем все они родились через одинаковые промежутки времени.
В тот год, когда Светлане было 10 лет, сумма квадратов возрастов детей равнялась сумме квадратов возрастов родителей. Треть суммы возрастов родителей равна седьмой части суммы возрастов детей (считаем только целое число лет).
Сколько было тогда каждому из детей и родителям, если известно, что муж Анны Савельевны - Максим Сергеевич старше её?
Решение.
Пусть дети рождались через t лет, тогда сумма квадратов детей
S1 = 10 + (10 + t) + … + (10 + 11t);
S1 = 120 + 0,5 · (t + 11t) · 11;
S1 = 6 · (20 + 11).
Пусть сумма возрастов родителей S2 = х + у.
По условию S2 : 3 = 6 · (20 + 11t) : 7;
20 + 11t кратно 7 при t = 2.
Другие значения t > 2 нереальны.
Определился возраст каждого из детей:
10, 12, …, 32;
S1 = 252,
S2 = 252 : 7 · 3 = 108.
Сумма квадратов возрастов детей равна 5864.
Принимая возраст Анны Савельевны за х, находим возраст родителей:
х2 + (108 - х)2
и по условию х2 + (108 - х)2 = 5864
или х2 - 108х + 2900 = 0,
откуда х1 = 58, х2 = 50. Значит, Анне было 50, Максиму - 58 лет.
Ответ
Возраст детей: 10, 12, …, 32;
Анне Савельевне 50 лет, Максим Сергеевичу 58 лет.
Памятные даты
Известно, что:
а) цифры года его рождения и года смерти одинаковы;
б) сумма цифр года рождения равна 14;
в) цифра единиц года рождения в 4 раза больше цифры единиц года смерти.
Определите даты жизни человека.
Ответ.
1814 - 1841 - годы жизни М.Ю. Лермонтова
Из жизни Дефурнеля
Некогда в отрывном календаре были приведены любопытные факты из биографии француза Пьера Дефурнеля. он был отцом трех сыновей, родившихся в разных веках. Он сам и старший сын родились в XVII веке. Женился на девятнадцатом году жизни. Через год стал отцом первого сына. Спустя 37 лет женился второй раз. Через год стал отцом второго сына. А еще через 43 года родилась будущая его третья жена. Через 19 лет после этого они поженились. через год родился третий сын. Спустя 8 лет Пьер Дефурнель умер.
Установите годы рождения Пьера Дефурнеля, сыновей, третьей жены и годы, когда женился Дефурнель и когда он умер.
Решение.
Пусть год рождения Дефурнеля 1601 + х.
Тогда для года рождения первого сына имеем:
1601 + х + 19 < 1701, т.е.
х < 81.(1)
Для года рождения второго сына:
1701 ≤ 1601 + х + 19 + 38 < 1801, или
43 ≤ х < 143.(2)
Третий сын родился через 63 года после второго сына, но
19 + 38 + 63 > 100,
следовательно он родился в XIX веке, и для его года рождения имеем:
1801 ≤ 1601 + х + 19 + 38 + 63 < 1901, т.е.
80 ≤ х < 180.(3)
Сопоставляя (1), (2) и (3), получим 80 ≤ х < 81, или
х = 80.
Итак, Пьер Дефурнель родился в 1681 году и жил 128 лет.
Остальные сведения легко получить из условия задачи.
Ответ. Пьер Дефурнель родился в 1681 году и жил 128 лет.
Две сестры
Пятнадцать лет назад Нушабе была в 5 раз старше своей младшей сестры Тунзале, а через 20 лет Нушабе будет в 1,5 раза старше Тунзале.
Найдите возраст сестер.
Решение.
Пусть 15 лет назад Тунзале было х лет, Нушабе у = 5х лет. Через (15 + 20) лет будет по условию
5х + 35 = (х + 35) × 1,5,
т.е. х = 5, у = 25.
Теперь Тунзале 20 лет, а Нушабе 40 лет.
Ответ.
Тунзале 20 лет, Нушабе 40 лет.
Сколько лет Игнату?
Игнату сейчас вчетверо больше лет, чем было его сестре в тот момент, когда она была вдвое моложе его.
Сколько лет сейчас Игнату, если через 15 лет ему и сестре будет вместе 100 лет?
Решение.
Игнат
Сестра
Тогда
2х
х
Сейчас
4х
3х
Через 15 лет
4х + 15
3х + 15
Для решения задачи воспользуемся таблицей.
Уравнение: (4х + 15) + (3х + 15) = 100;
7х + 30 = 100;
7х = 70;
х = 10.
Если х = 10, то 4х = 40.
Ответ. Игнату сейчас 40 лет.
Приложение 1.8
Часы
Правдивый Федя
Правдивый Федя всегда говорит только правду, но однажды, когда ему задали два раза подряд один и тот же вопрос, он дал на него разные ответы.
Могло ли такое быть?
Ответ.
Можно, например, дважды спросить у него: "Сколько сейчас времени?"
Часы остановились
КАНТ Иммануил
(1724-1804)
Эту замечательную историю рассказывают про одного из крупнейших немецких философов И. Канта. Как-то вечером он обнаружил, что его настенные часы остановились. Чтобы узнать время, он отправился в гости к одному из своих друзей. Пробыв там некоторое время, он вернулся домой и поставил правильно стрелки часов.
Как ему это удалось?
Ответ: Вероятно дело происходило так: Кант завел свои настенные часы и пошел в гости. Узнав там точное время, он возвратился обратно (при этом не забыв учесть время, проведенное в гостях). Дома он по показаниям часов определил, сколько времени он был в пути. Разделил эти данные на два и прибавил к показаниям часов приятеля. Это и будет точное время.
Стрелки часов
Через какое время после 12.00 минутная стрелка впервые догонит часовую?
Решение.
В 13.00 минутная стрелка будет отставать от часовой на 5 минутных делений. "До встречи" часовая стрелка пройдет х делений, а минутная - 12х делений.
Из уравнения х + 5 = 12х
получим, что х = 5/11
минутных делений циферблата.
Ответ: После 12.00 минутная стрелка впервые догонит часовую через 1 час и 5 целых 5/11 минуты.
Точное время
Какие часы чаще показывают точное время: те, которые отстают на одну минуту или те, которые стоят?
Решение.
Часы, отстающие в сутки на 1 минуту, показывают точное время один раз в два года. Часы, которые стоят, показывают точное время дважды в сутки.
Ответ: Часы, которые стоят, чаще показывают точное время, чем те, которые отстают на одну минуту.
Приложение 1.9
Фигуры из спичек
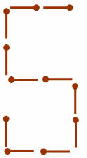
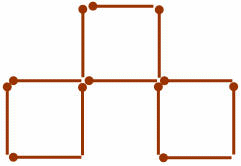
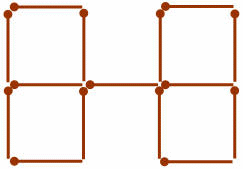
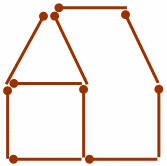
1. Из спичек построен "дом". Переложите 2 спички так, чтобы он повернулся другой стороной:
Ответ:
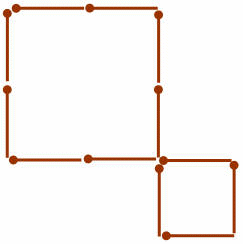
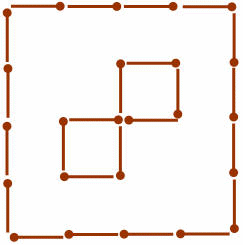
2. Составьте из 15-ти спичек фигуру, изображенную на рисунке. Переложите теперь 2 спички так, чтобы образовалась фигура, составленная из пяти равных квадратов:
Ответ.
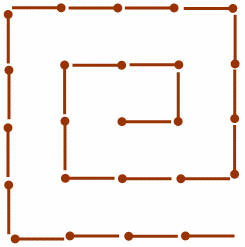
3. Переложите 4 спички таким образом, чтобы образовались три квадрата:
Ответ.
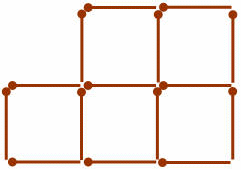
4. В фигуре, изображенной на рисунке, переложите 5 спичек так, чтобы получилось всего два квадрата:
Ответ.
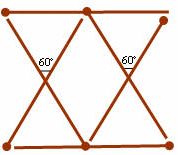
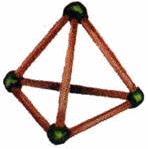
5. С помощью кусочков пластилина соорудили модель пирамиды из шести спичек одинаковой длины и заметили, что в этой конструкции содержится четыре равных равносторонних треугольника.
А нельзя ли выложить из тех же шести спичек четыре равных равносторонних треугольника, расположенных в одной плоскости?
Ответ.
6. Из двух квадратов сделайте пять, переложив три спички:
Ответ.
7. Задачи со спичками.
1) Положи 12 спичек так, чтобы получилось 5 квадратов.
2) В фигуре, построенной в предыдущей задаче, убери 4 спички так, чтобы осталось два одинаковых квадрата.
3) В фигуре задачи № 1 убери 2 спички, чтобы осталось два квадрата разного размера.
Приложение 1.10
Переливания
Парное молоко
Бидон емкостью 10 л наполнен парным молоком. Требуется перелить из этого бидона 5 л молока в семилитровый бидон, используя при этом трехлитровый бидон.
Решение.
Будем "шаги" переливаний записывать в виде строки из трех чисел.
При этом сосуды размещены слева направо по мере убывания их вместимости:
Шаги
Бидон
10 л
7 л
3 л
1-й
3
7
0
2-й
3
4
3
3-й
6
4
0
4-й
6
1
3
5-й
9
1
0
6-й
9
0
1
7-й
2
7
1
8-й
2
5
3
Задача №2 Как набрать два литра воды, имея семилитровое ведро и трехлитровую банку?
Шаги
3 л банка
7л ведро
1-й
0
7
2-й
3
4
3-й
0
4
4-й
3
1
5-й
0
1
6-й
1
7
7-й
3
5
8-й
0
5
9-й
3
2
Задача №3 Имеется 12 л ведро с керосином и два пустых ведра - одно 8л, а другое 5л. Разделите керосин пополам.
Шаги
12 л
8 л
5 л
1-й
12
0
0
2-й
4
8
0
3-й
4
3
5
4-й
9
3
0
5-й
9
0
3
6-й
1
8
3
7-й
1
6
5
8-й
6
6
0
Задача №4 Имеется 8 л ведро с молоком и два пустых ведра - одно 3л, а другое 5л. Разлейте молоко пополам в два ведра.
Шаги
8 л
5 л
3 л
1-й
8
0
0
2-й
3
5
0
3-й
3
2
3
4-й
6
2
0
5-й
6
0
2
6-й
1
5
2
7-й
1
4
3
8-й
4
4
0
Приложение 1.11
Фальшивые монеты
Бракованная деталь
Токарь выточил 27 деталей, среди них одна оказалась нестандартная. По виду ее отличить от остальных невозможно.
За какое наименьшее число взвешиваний на чашечных весах можно определить бракованную деталь, если известно, что она тяжелее, чем стандартная.
Решение.
1) Разложим 27 деталей на 3 кучки по 9 деталей. С помощью первого взвешивания определим, в какой из трех кучек находится бракованная деталь. Для этого положим по 9 деталей на каждую чашечку весов, а 9 деталей отложим в сторону:
а) если весы в равновесии, то бракованная деталь находится среди деталей, отложенных в сторону;
б) если равновесия не будет, то нестандартная деталь находится в опущенной чашке весов, т.е. в более тяжелой кучке.
2) Далее возьмем ту кучку, где лежит нестандартная деталь, и разложим имеющиеся там 9 деталей опять на 3 кучки, но уже по 3 детали. С помощью второго взвешивания определим, в какой из трех кучек находится бракованная деталь (см. пункт 1 а, б).
3) С помощью третьего взвешивания определим, какая из трех деталей, находящаяся в более тяжелой кучке, бракованная. Для этого положим по одной детали на чашки весов, а третью отложим в сторону:
а) если весы в равновесии, то бракованная деталь не на весах;
б) если равновесия не будет, то нестандартная деталь находится на опущенной чашке весов, т.е. более тяжелая.
Ответ: За три взвешивания.
Задача №2 Из трёх монет одна фальшивая, она легче остальных. За сколько взвешиваний на чашечных весах без гирь можно определить, какая именно монета фальшивая?
Решение: Требуется одно взвешивание: положим по одной монете на каждую чашку весов. Возможны два случая:
1) весы находятся в равновесии, тогда третья монета фальшивая;
2) равновесия нет, в этом случае фальшивая монета там, где вес меньше.
Ответ: одно взвешивание.
Приложение 1.12
Расположения
Мыши любят сыр
Мышка грызет куб сыра с ребром 3, разбитый на 27 единичных кубов. Когда мышка съедает какой-либо кубик, она переходит к следующему кубику, имеющему общую грань с предыдущим.
Может ли мышка съесть весь куб, кроме центрального кубика?
Решение.
Раскрасим все единичные кубики, кроме центрального, в "шахматном" порядке. Так как мышка съедает белые и черные кубики по очереди, то число белых кубиков не может превышать числа черных более, чем на один. Но у нас получилось 14 белых кубиков и 12 черных, следовательно, мышка съесть весь куб, кроме центрального не может.
Ответ: Мышка съесть весь куб, кроме центрального кубика, не может.
Танец жуков
Представьте себе, что вам удалось поймать 25 жуков и рассадить их по одному на каждой клетке куска шахматной доски размером 5 × 5. Предположим теперь, что каждый жук переполз на соседнюю по горизонтали или по вертикали клетку этого куска доски.
Останутся ли при этом пустые клетки?
Решение.
Так как число клеток доски 5 × 5 нечетно, то черных и белых клеток не может быть поровну. Предположим, что черных клеток больше. Тогда одна из черных клеток обязательно останется пустой, так как на черные клетки переползают только те жуки, которые сидят на белых клетках.
Ответ: Да.
Приложение 1.13
Маленькие хитрости
Как белке выиграть орехи?
Имеются 6 орехов. Белка и заяц берут по очереди по одному, по два или по три ореха. Проигрывает тот, кому достался последний орех.
Как правильно играть белке (начинающему), чтобы не проиграть?
Решение.
Рассмотрим три варианта.
1) Начинающий берет три ореха. Тогда противник, взяв 2 ореха, выигрывает, так как начинающему игру остается один орех.
2) Начинающий берет 2 ореха, тогда противник, взяв 3 ореха, выигрывает, так как начинающему игру достается 1 орех.
3) Начинающий берет один орех. Тогда при любом числе орехов, взятым противником (1; 2; 3), начинающий должен брать столько орехов, чтобы остался один орех (4 - 1 = 3; 4 - 2 = 2; 4 - 3 = 1).
Ответ: Таким образом, взяв сначала 1 орех и действуя далее правильно (беря столько орехов, чтобы они с числом, взятым противником, давали в сумме 4), начинающий всегда выигрывает.
Любит - не любит?
Две девочки играют в игру - отрывают лепестки у ромашки. За один ход можно отрывать либо 1 лепесток, либо 2 лепестка расположенных друг с другом. Побеждает та девочка, которая оторвала последний лепесток.
Кто выигрывает при правильной игре?
Решение.
При правильной игре выигрывает вторая девочка.
При любом первом ходе есть возможность сделать такой второй ход, который разобьет все оставшиеся лепестки на две симметричные части (смотри рисунок).
Далее вторая девочка делает ходы симметрично ходам первой.
Древний грек
Некий древний грек родился 7 января 40 года до нашей эры, а умер 7 января 40 года нашей эры.
Сколько лет он прожил?
Ответ.
Древний грек прожил 79 лет.
День недели
В некотором месяце три воскресенья пришлись на четные числа.
Какой день недели был 20-го числа этого месяца?
Ответ.
Воскресенья в одном месяце, чередуясь, выпадают на четные и нечетные числа, а так как три из них выпали на четные чмсла, то всего в этом месяце было 5 воскресений, поэтому первое из них могло быть только 2-го числа, откуда 20-е число - четверг.
Пять воскресений
Может ли быть в одном месяце пять воскресений?
Ответ: Да, например, 1, 8, 15, 22, 29-е.
Какой сегодня день недели?
Известно, что "когда послезавтра станет вчера, то сегодня будет так же далеко от воскресенья, как тот день, который был сегодня, когда вчера было завтра".
Какой сегодня день недели?
Ответ.
Среда. Тогда "послезавтра станет вчера" - пятница, а "тот день, который был сегодня, когда вчера было завтра" - понедельник.
Когда у Серика день рождения?
Серик как-то сказал: "Позавчера мне было 10 лет, а в будущем году мне исполнится 13 лет".
Когда у Серика день рождения?
Ответ.
День рождения Серика - 31 декабря, а разговор происходил на следующий день, то есть 1 января.
Приложение 1.13
Логические задачи
Странный вопрос
Федя всегда говорит правду, а Саша всегда врет. Им задали один и тот же вопрос, а они дали на него одинаковые ответы.
Могло ли такое быть?
Ответ: Можно спросить: "Говорите ли Вы правду?" На этот вопрос и правдивый человек, и лжец должны ответить "да".
На крыльце
Нa крыльце дома сидят рядом мальчик и девочка.
Саша говорит: "Я - мальчик".
Женя говорит: "Я - девочка".
Если, по крайней мере, один из детей врет, то кто из них мальчик, а кто девочка?
Ответ: Из того, что один из них врет, следует, что врет и второй. Следовательно, Саша - девочка, а Женя - мальчик.
Три попугая
Один из попугаев А, В, С всегда говорит правду, другой всегда врет, а третий - иногда говорит правду, иногда врет. На вопрос: "Кто В?" они ответили:
А: - Лжец.
В: - Я хитрец!
С: - Абсолютно честный попугай.
Кто из попугаев лжец?
Ответ: А всегда говорит правду, В - лжец, С - хитрец.
Аборигены и пришельцы
На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, пришельцы всегда лгут. Путешественник, приехавший на остров, нанял туземца-островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал проводника узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал: "Туземец говорит, что он - абориген". Кем был проводник: пришельцем или аборигеном?
Решение.
Из условия задачи ясно, что кем бы ни был встречный туземец, он назовет себя аборигеном (абориген - потому что всегда говорит правду, пришелец - потому что всегда лжет). Следовательно, проводник сказал правду и потому он принадлежит к племени аборигенов.
Ответ: Проводник - абориген.
В сенате
В сенате страны рыцарей и лжецов - 100 сенаторов. Каждый из них либо рыцарь, либо лжец. Известно, что:
1) по крайней мере, один из сенаторов - рыцарь;
2) из двух произвольно выбранных сенаторов, по крайней мере, один - лжец.
Определите, сколько в сенате рыцарей и сколько лжецов?
Решение.
Только один из сенаторов - рыцарь. То, что хотя бы один рыцарь среди сенаторов имеется, следует из первого утверждения, существование второго рыцаря противоречит второму утверждению.
Ответ: В сенате один рыцарь, остальные - лжецы.
Куда пропал доллар?
Три человека пообедали, заплатив 30 долларов (по 10 долларов за каждого) и ушли. Через некоторое время повар заметил, что обсчитал их на 5 долларов, и послал поваренка отдать их. Поваренок отдал 3 доллара (по 1 доллару на каждого), а 2 доллара забрал себе.
Три раза по 9 долларов и 2 доллара у поваренка, получается 29 долларов.
Куда пропал доллар?
Решение.
Доллар никуда не делся. Произведем расчет. Обед стоил 25 долларов, мальчик оставил себе 2 доллара, поэтому обед клиентам обошелся в 27 долларов. 3 доллара им вернули. Чтобы расчет был правильным, нужно к 27 долларам прибавить 3 доллара, а не 2. Все сходится.
Ответ: Доллар никуда не пропадал.
Рассеянные свидетели
Браун, Джонс и Смит - свидетели ограбления банка. Браун показал, что преступники скрылись на синем "Бьюике". Джонс утверждал, что это был черный "Крайслер", а Смит, что это был "Форд", но не синий. По рассеянности, каждый из них указал правильно либо только марку, либо только цвет машины.
На какой машине уехали преступники?
Решение.
Автомобиль не мог быть синим, так как иначе в показаниях и Смита, и Джонса должна быть верно указана марка машины, что одновременно невозможно. Значит Браун правильно указал марку машины, а Джонс и Смит верно указали цвет машины. Следовательно, преступники уехали на черном "Бьюике".
Ответ: Преступники уехали на черном "Бьюике".
Кого допросить первым?
Показания трех подозреваемых по делу противоречат друг другу, причем, Смит обвиняет во лжи Брауна, Браун - Джонса, а Джонс говорит, что не следует верить ни Брауну, ни Смиту.
Кого бы Вы, будучи следователем, допросили первым?
Решение.
Кто из подозреваемых мог сказать правду? Это не мог быть Джонс, так как тогда высказывание Смита о том, что Браун лжет будет неверно, а это противоречит высказыванию Джонса. Не мог быть и Браун, так как тогда высказывание Джонса о том что Смит лжет...
Ответ: ...
Из протокола допроса
Из протокола допроса трех известных А, В и С (фамилии гангстеров скрыты в интересах следствия):
А:
1) Я не совершал преступления.
2) В день преступления меня не было в городе.
3) Преступление совершил С.
В:
1) Преступник - С.
2) Если бы я совершил преступление, я бы не сознался.
3) У меня и так много денег.
С:
1) Я не совершал преступления.
2) Я давно ищу хороший портфель.
3) А не было в городе в день преступления.
Известно, что преступление мог совершить только один из них. В ходе следствия выяснилось, что из трех заявлений каждого гангстера два верных, а одно неверное.
Кто совершил преступление?
Решение.
А - не преступник, ведь иначе его высказывания ложны, что противоречит условию задачи. С тоже не преступник, иначе все три высказывания А были бы истиной, что также противоречит условию задачи. Следовательно, преступник - В.
Ответ: Преступник - В.
Дело Брауна, Джонса и Смита
Один из них совершил преступление. В процессе расследования каждый из них сделал по два заявления:
Браун:
1) Я - не преступник.
2) Джонс - тоже.
Джонс:
1) Браун - не преступник.
2) Преступник - Смит.
Смит:
1) Преступник - Браун.
2) Я - не преступник.
В процессе следствия было установлено, что один их них дважды солгал, другой дважды сказал правду, а третий - один раз солгал и один раз сказал правду. Кто совершил преступление?
Решение.Преступником не может быть Джонс, так как в этом случае ни один из подсудимых не солгал два раза, что противоречит условию задачи. Им не может быть и Смит, так как в этом случае нет подсудимого, солгавшего ровно один раз. Единственно возможный вариант - преступление совершил Браун.
Ответ: Преступление совершил Браун.
Кто участвовал в ограблении?
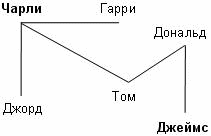
Известно, что из шести гангстеров ровно двое участвовали в ограблении. На вопрос, кто участвовал в ограблении, они дали следующие ответы:
Гарри: Чарли и Джордж.
Джеймс: Дональд и Том.
Дональд: Том и Чарли.
Джордж: Гарри и Чарли.
Чарли: Дональд и Джеймс.
Поймать Тома не удалось.
Кто участвовал в ограблении, если известно, что четверо из гангстеров верно назвали одного из участников ограбления, а один назвал неверно оба имени?
Решение.
Каждый отрезок на рисунке - это показания одного из гангстеров. Напрмер: отрезок Чарли-Гарри - это показания Джорджа. У всех отрезков, кроме одного, одна вершина соотвествует гангстеру, участвовавшему в ограблении, а вторая - не учавствовавшему. В двух точках, которые соотвествуют преступникам, должны сходиться ровно четыре отрезка.
Ответ. Грабители - Чарли и Джеймс.
Кто украл чемодан?
Один из четырех гангстеров украл чемодан с деньгами. На допросе Алекс сказал, что чемодан украл Луи. Луи утверждал, что виновник Том. Том заверял следователя, что Луи лжет. Жорж настаивал на том, что он не виноват. В ходе расследования выяснилось, что только один из гангстеров сказал правду. Кто?
Решение. Так как из утверждений Луи и Тома одно верно, то Жорж соврал и, следовательно, преступник он.
Ответ: Правду сказал Том.
Приложение 1.15
Задания для интеллектуального марафона «Олимпик» 5 класс
1) Вместо * подставить цифры, чтобы получилось 1 4 * * | * 7
верное равенство. Результат проверить умножением. - --------
* * 5 * *
------
* *
* 1
-------
0
-
В двузначном числе количество десятков в 4 раза больше количества единиц, а сумма цифр этого числа равна наименьшему двузначному числу. Что это за число?
-
Ученик за 370 тенге купил книгу, тетрадь, ручку и карандаш. Тетрадь, ручка и карандаш стоят вместе 190 тенге; книга, ручка и карандаш стоят вместе 350 тенге. Тетрадь и карандаш стоят вместе 50 тенге. Сколько стоит каждый предмет?
-
Встретились 3 друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас блондин, другой - брюнет, третий - рыжеволосый, но ни у одного нет волос того цвета, на который указывает его фамилия», - заметил брюнет. «Ты прав», - сказал Белов. Каков цвет волос у художника?
Примечание: брюнет - черноволосый, блондин - беловолосый.
-
Зоина бабушка развела гусей и кроликов, у которых вместе 25 голов и 54 лапки. Сколько гусей и сколько кроликов у бабушки?
Приложение 1.16
Задания для интеллектуальной игры: «По волнам математики»
Вопросы капитанам:
-
Из Киева в Одессу вышел автобус и шел со скоростью 80 км/ч. Другой автобус вышел ему на встречу из Одессы в Киев и шел со скоростью 90 км/ч. На каком расстоянии автобусы будут друг от друга за 1 час до их встречи?
-
Мама дала Зое денег, чтобы она в школьном буфете купила завтрак. Когда Зоя вернулась из школы, то перед мамой отчиталась так: «
 всех денег я истратила на булочку,
всех денег я истратила на булочку,  - на чай, а
- на чай, а  - на конфеты». Мама догадалась, что дочь истратила все деньги. Как она догадалась?
- на конфеты». Мама догадалась, что дочь истратила все деньги. Как она догадалась? -
Портной имеет кусок сукна в 16 м, от которого он отрезает ежедневно по 2 м. По истечении скольких дней он отрежет последний кусок?
-
Сколько ударов в сутки делают часы с боем (бьют только в ровно)?
-
Два лесоруба работают в лесу. Решили на обед сварить кашу. Первый лесоруб высыпал в кастрюлю 2 стакана крупы, а второй - 1 стакан. Как только каша была готова, к ним подошел проголодавшийся охотник. Разделили они кашу поровну, и каждый съел свою долю. Охотник после обеда нашел в своем кармане 50 тенге и сказал: «Не обессудьте, братцы, больше при себе ничего нет. Поделитесь по справедливости». Как должны разделить деньги лесорубы?
Вопросы лоцманам:
-
Незнайка может отложить угол в 19º. Как ему отложить угол в 1º?
Подсказка: 19º· 19 = 361º.
2. Два отца и два сына съели три яблока, каждому досталось по целому яблоку. Как это могло случиться?
-
Сколько будет десятков, если три десятка умножить на два десятка?
-
Чему равно произведение всех цифр?
Вопросы радистам
-
В строки таблицы впишите названия чисел 900, 600, 1000, 500. В одном из столбцов прочтете название числа.
-
Расшифруйте высказывание Карла Фридриха Гаусса:
«Акитаметам - ацирац куан, акитемфира - ацирац икитаметам».
-
В заглавии, каких литературных произведений встречаются названия чисел?
-
Расстояние между двумя телеграфными столбами равно 50 м. Сколько телеграфных столбов нужно установить на расстоянии 500 м?
Вопросы штурманам
-
Необходимо заправить корабль. Бидон, емкость которого 10 л, наполнен керосином. Имеются еще пустые сосуды в 7 л и 2 л. Как разделить керосин в два сосуда по 5 л в каждый?
-
Каждая спичка имеет длину 4 см 5 мм. Как из 15 спичек сложить метр?
-
Какой сейчас час, если оставшаяся часть суток вдвое больше прошедшей?
-
Поставьте в таблице недостающие числа (найти закономерность).
-
2
8
3
5
25
2
3
?
1
0,1
0,01
?
Вопросы кокам
-
Вычислите массу рыбы в килограммах, заменив рисунки на числа:
○4 =∆; ☼4 =◊ кг; 8·207 = □; □ - 1500 = ○; ∆ + 61 = ☼.
-
В классе на каждых трех мальчиков две девочки. Если в классе 30 человек, каков процент девочек?
-
Каким образом получить 50, удаляя из 40 десять?
-
Устная задача на внимательность.
Вопросы юнгам
-
Один человек купил трех коз и заплатил 6000 тенге. Спрашивается: «по чему каждая коза пошла»?
-
Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько летело уток?
-
Мельник пришел на мельницу. В каждом из четырех углов он увидел по три мешка, на каждом мешке сидело по три кошки, а каждая кошка имела при себе троих котят. Сколько ног было на мельнице?
-
Ребята пилят бревно на метровые куски. Отпиливание одного такого куска занимает 1 минуту. За сколько минут они распилят бревно длиной 5 м?
Вопросы врачам.
-
Укажите десятичную дробь, которая соответствует температуре здорового человека.
-
На руках человека 10 пальцев. Сколько пальцев на 10 руках?
-
Поставьте знаки и скобки, чтобы равенство было верным:
1 2 = 2; 3 2 1 = 2; 1 2 3 4 5 = 2.
4. Буратино и два его друга собрали орехи. Ночью Буратино проснулся и съел  всех орехов, после чего лег спать. Затем один из его друзей встал, не зная, что Буратино просыпался, и съел
всех орехов, после чего лег спать. Затем один из его друзей встал, не зная, что Буратино просыпался, и съел  оставшихся орехов. Через некоторое время другой его друг, проснувшись, съел
оставшихся орехов. Через некоторое время другой его друг, проснувшись, съел  оставшихся орехов. На утро осталось всего 16 орехов. Сколько орехов собрали Буратино и его друг?
оставшихся орехов. На утро осталось всего 16 орехов. Сколько орехов собрали Буратино и его друг?
Приложение 1.17
Игра "Счастливый случай", состоящая из 5 геймов.
Оборудование:
-
Плакат с названием геймов:
1 гейм "Дальше… дальше… дальше"
2 гейм "Заморочки из бочки"
3 гейм "Темная лошадка"
4 гейм "Гонка за лидером"
5 гейм "Лирическая мозаика" -
Секундомер
-
Бочка с бочонками
-
Магнитофон с записью мелодии "Счастливый случай" (включается перед началом игры и каждым геймом)
-
Плакат "Обдумай цель раньше, чем дело начать"
-
Плакат "Видит око далеко, а ум еще дальше"
-
Плакат "Математика + удача = Счастливый случай"
Вступление
Дорогие ребята и уважаемые взрослые! Я рада приветствовать вас всех на игре "Счастливый случай".
Мой юный друг!
Сегодня ты пришел в этот класс,
Чтоб посидеть, подумать отдохнуть,
Умом своим на все взглянуть.
Пусть ты не станешь Пифагором,
Каким хотел бы, может быть,
Но будешь ты рабочим, а может быть ученым,
И будешь математику любить.
Вы не раз, ребята, принимали участие в разных играх, но в математической викторине "Счастливый случай" участвуете впервые. И для того, чтобы выиграть сегодня, не нужно забывать как говорят пословицы: "Обдумай цель раньше, чем дело начать", "Видит око далеко, а ум дальше".
Наши команды приготовились идти по нелегкому пути к победе. И сегодня они будут бороться не только за победу, но и за счастливый случай. И пусть Математика + удача принесут вам Счастливый случай.
Две команды, у каждой есть свое название.
-
Разыграть, какая из команд начнет отвечать первой.
-
В конце каждого гейма счетная комиссия объявляет итоговый результат каждой команды.
1 гейм "Дальше… дальше… дальше"
Каждая команда поочередно бросает игровой кубик (на пяти гранях кубика нанесены единицы, на одной грани - подкова):
1 - 1 балл за правильный ответ;
подкова - 3 балла за правильный ответ;
Каждая команда бросает кубик 6 раз.
Вопросы 1 команде:
-
За 3 мин. бревно распилили на полуметровые бревна, причем каждая распиловка занимала 1 мин. Найти длину бревна. (2 мин)
-
Тройка лошадей бежит со скоростью равной 15 км/ч. С какой скоростью бежит каждая лошадь? (15 км/ч)
-
Во сколько раз путь по лестнице на 16-й этаж дома длиннее пути на 4-й этаж дома? (В 5 раз)
-
Может ли сумма 4-х последовательных натуральных чисел быть простым числом? (Нет, она делится на 2)
-
Лена произнесла предложение, которое являлось верным. Коля его в точности повторил, но оно уже было неверным. Какое предложение произнесла Лена? (Меня зовут Лена)
-
3 курицы за 3 дня снесут 3 яйца. Сколько яиц снесут 9 кур за 9 дней? (27 яиц)
3 куры за 1 день - 1 яйцо
9 кур за 1 день 9 яиц
9 кур за 3 дня - 27 яиц
Вопросы 2 команде:
-
Пять ворохов сена и семь ворохов сена свезли вместе. Сколько получилось ворохов сена? (Один)
-
Какими нотами можно измерить расстояние? (Ми-ля-ми)
-
Волк и лиса соревновались в беге. Кто какое место занял, если известно, что волк был одним из первых, а лиса последней? (Лиса - 1, волк - 2)
-
Какой цифрой заканчивается произведение всех нечетных двухзначных чисел? (Цифрой 5)
-
За книгу заплатили 1 рубль и еще половину стоимости книги. Сколько стоит книга? (2 рубля)
-
Если из одной стопки тетрадей переложить в другую 10 штук, то тетрадей в стопках будет поровну. На сколько в одной стопке тетрадей было больше, чем в другой? (На 20 штук)
2 гейм "Заморочки из бочки"
Шесть пронумерованных бочонков. Тянуть бочонки (3 раза). Начинает команда, у которой на данный момент меньше очков.
Ведущий зачитывает команде вопрос, номер которого указан на бочонке. За правильный ответ - 2 балла.
-
Половина от половины равна половине. Найдите число (2)
-
Число 30 легко выразить тремя пятерками 5*5+5=30. А как можно это число выразить другими тремя цифрами? (6*6-6=30, 33-3=30, 33+3=30)
-
В коробке лежат карандаши: 4 красных и 3 синих. В темноте берут карандаши. Сколько нужно взять карандашей, чтобы в них было не менее 1 синего? (5)
-
Известно, что один носорог весит 1 т 700 кг. Сколько носорогов сможет увезти машина грузоподъемностью 5 тонн? А сколько крокодилов сможет увезти все та же машина, если один крокодил 170 кг? (2 носорога, 9 крокодилов, т.к. 2 носорога уже в машине)
-
Математик, оказавшись случайно в небольшом городке и желая хоть как-то убить время, решил подстричься. В городе имелось лишь два мастера, у каждого из них своя парикмахерская. Заглянув к одному мастеру, математик увидел, что в салоне грязно, сам мастер одет неряшливо, небрежно подстрижен. В салоне другого мастера было идеально чисто, а владелец был безукоризненно одет и аккуратно подстрижен. Поразмыслив, математик отправился к первому парикмахеру. Не могли бы вы объяснить причину столь странного на первый взгляд решения математика? (Поскольку в городе лишь два парикмахера, то каждый мастер вынужден стричься у другого. Математик выбрал того из мастеров, кто лучше подстриг своего конкурента.)
-
Представьте число "2" в виде суммы четырех различных дробей, числители которых 1, а знаменатели натуральные числа. (1/1+1/2+1/3+1/6)
3 гейм "Темная лошадка"
Игра с командами. Им предлагается угадать, кто проведет этот гейм.
-
она учитель ________
-
на "отлично" закончила среднюю школу
-
на "отлично" закончила ___________
-
общительна
-
любит петь и т.п
-
умеет решать наитруднейшие задания по математике
-
принимает участие, как член жюри, на городских олимпиадах, турнирах города.
Гость объясняет правила 3-го гейма.
Он загадывает имена великих математиков, читает наиболее известные факты из их биографии.
1 команде: Человек, который хотел быть и юристом, и философом, и офицером, но стал математиком. Он первый ввел в математику прямоугольную систему координат. (Декарт)
2 команде: Ученый, который нашел отношение длины окружности к диаметру. (Архимед)
1 команде: Кто написал знаменитое произведение "Начало", которое сделало имя этого математика бессмертным? (Евклид)
2 команде: Ученый, который известен как создатель школы математиков. Он открыл замечательное свойство прямоугольных треугольников. (Пифагор)
На доске вывешиваются портреты великих математиков:
Архимед, Декарт, Пифагор, Лобачевский, Евклид, С. овалевская.
Ученикам заранее сообщают фамилии этих ученых для ознакомления с биографиями.
В 3-м гейме команды получают 5 баллов за правильный ответ.
4 гейм "Гонка за лидером"
Каждой команде задаются вопросы. За каждый правильный ответ команда получает один балл. Если в течение 3-х секунд после прочтения вопроса команда не дает никакого ответа, ведущий зачитывает правильный ответ и задает следующий вопрос. Вопросы задавать начинают той команде, у которой на данный момент меньше очков.
Вопросы для 1-ой команды:
-
Какая разница между числом и цифрой? (10 цифр, чисел много.)
-
Что называют биссектрисой угла? (Луч, выходящий из вершины угла и делящий угол пополам.)
-
Сколько музыкантов в квартете? (4)
-
Наименьшее натуральное число? (1)
-
Как называется дробь, у которой числитель меньше знаменателя? (Правильная)
-
Соперник нолика. (Крестик)
-
Наука о числах, их свойствах и действиях над ними. (Арифметика)
-
Сколько дней в летних каникулах? (92)
-
Сотая доля числа. (Процент)
-
Есть у уравнения и растения. (Корень)
-
То, на что делят. (Делитель)
-
Сколько получится десятков, если два десятка умножить на три десятка? (60)
-
Делится ли число 111*121*131*141-151 на 10? (Да, т.к. оно оканчивается на ноль.)
-
На лесопильном заводе каждую минуту машина отпиливает от бревна кусок в 1 м. Через сколько она распилит кусок в 6 м? (5 минут)
-
Петух, стоя на одной ноге, весит 3 кг. Сколько он весит, стоя на двух ногах? (3 кг)
-
Найдите модуль числа (-6). (6)
-
41 - это простое число? (Да)
-
Какие прямые пересекаются под прямым углом? (Перпендикулярные)
-
Формула для периметра квадрата. (Р=4а)
Вопросы для 2-ой команды:
-
Излишек при нахождении частного. (Остаток)
-
Записывается с помощью цифр. (Число)
-
Отрезок, делящий круг пополам. (Диаметр)
-
Он бывает натуральным. (Ряд)
-
Число 666 увеличили в 1,5 раза, не производя над ним никаких арифметических действий. Какое число получили? (999)
-
Какая мера длины была распространена на Руси? (Локоть, сажень)
-
Сколько будет 52, 62, угол в квадрате? (90° )
-
Сумма длин всех сторон треугольника. (Периметр)
-
Трудный путь от условия к ответу. (Решение)
-
Сколько пьес во временах года П. И. Чайковского? (12)
-
Число противоположное 5. (-5)
-
Другое название угломера. (Транспортир)
-
Место, на котором стоит цифра в записи числа. (Разряд)
-
Метод Эратосфена, в котором простые числа "отсеиваются" от составных. (Решето)
-
Число, обратное 2. (1/2)
-
Как называется верхняя часть дроби? (Числитель)
-
Сколько концов у 3,5 палок? (8)
-
Назовите число, "разделяющее" положительные и отрицательные числа. (0)
-
Как называются прямые, которые не пересекаются? (Параллельные или скрещивающиеся)
5 гейм "Лирическая мозаика"
Каждой команде дается задание придумать четверостишие на заданные рифмы:
Остаток - недостаток
Свойство - устройство
Копейка - линейка
Число - весло
Куб - дуб
Скобка - коробка
Закон - дракон
2 балла за одно придуманное четверостишие.
В конце 5-го гейма подсчитывается общий итог игры. Победителям - медали в форме подковы. Другой команде - призы.
Приложение 2
Технологическое обеспечение курса.
Приложение 2.1
Описание приемов и средств организации УВП.
Мини - лекция. Как правило, это занятия, на которых излагается значительная часть теоретического материала изучаемой темы. Лекционная форма проведения занятия целесообразна:
-при изучении нового материала, мало связанного с ранее изученным;
- при рассмотрении сложного для самостоятельного изучения материала;
- подаче информации крупным блоком;
-при выполнении определённых видов заданий по одной или нескольким темам, разделам и т.д.;
- при применении изучаемого материала для решения практических задач.
Структура лекции определяется выбором темы и цели занятия.
Семинар. Семинары характеризуются, прежде всего, двумя взаимосвязанными признаками: самостоятельным изучением учащимися программного материала и обсуждением на занятии результатов их познавательной деятельности. На них ребята учатся выступать с самостоятельными сообщениями, дискутировать, отстаивать свои суждения. Семинары способствуют развитию познавательных и исследовательских умений учащихся, повышению культуры общения.
Практикум. Практикумы, помимо решения своей специальной задачи - усилия практической направленности обучения, должны быть тесным образом связаны с изученным материалом, а также способствовать прочному, неформальному его усвоению. Основной формой их проведения являются практические и лабораторные работы, на которых учащиеся самостоятельно упражняются в практическом применении усвоенных теоретических знаний и умений.
Атака мыслей. В школе применяется при опросе, изучении нового учебного материала, повторении и обобщении пройденного, при решении проблем, при составлении планов класса и т.д. Может применяться на всех предметах. Цель данной работы - решение проблемы посредством объединения творческих мыслей учащихся, созданию «коллективного мозга».
Ролевая игра.
Проводится в форме круглого стола, заседания экспертной комиссии, форума и т.д. Класс делится на группы по 4 -6 человек, каждой из которой присваивается роль: Реалисты. Оптимисты, Пессимисты, Аналитики, Критики и Наблюдатели. В каждой группе начинает Ведущий.
Учитель ставит проблему и предлагает её рассмотреть только с позиции своей роли. Через определённое время подготовки (10 -15 минут ) каждая группа высказывает свою ролевую точку зрения, аргументирует и подтверждает её схемой, рисунком, отчетом, мини - проектом.
После выступления первых трёх основных групп выступает группа критиков, которая критикует слабые мета, задает вопросы трём группам. Аналитики анализируют, степень аргументированности позиции каждой группы.
Группа « наблюдателей» подводить итог деятельности всех групп, выделяет наиболее активных участников, заполняя оценочный бланк.
Игра «Счастливый случай»
Оборудование:
1.Мешок или бочонок с шарами.
2.Секундомер.
3. Общий оценочный лист.
4. Фишки.
5.Домашние вопросы (по два на каждую команду).
6. Задания для конкурсов.
7. Образцы ответов.
Ход игры
Класс делится на две команды, каждая команда имеет своего Капитана и название.
1 гейм. «Разминка».
Командам задают по 10 вопросов, на обсуждение которых дается 5 минут. Отвечает представитель команды, а команда соперников контролирует правильность ответов по образцу. Выигрывает та команда, которая правильно ответила на большее количество вопросов.
2 гейм. «Заморочки из бочки».
Участники команды достают из бочонка шарики с номерами. Ведущий читает на каждый номер загадку или вопрос. После обсуждения капитаны команд дают ответы.
3 гейм. «Темная лошадка».
Побеждает та команда, которая быстрее ответит на вопрос ведущего. Если ответ готов, команда поднимает сигнальный флажок или руку.
4 гейм. «Ты - мне, я - тебе».
Команды задают по два вопроса друг другу (домашнее задание).
5.»Гонка за лидером».
Отвечают на вопросы все участники. Выигрывает та команда, которая даст больше правильных ответов. Те из ребят, которые ответили на большее число вопросов (4-7),
Зарабатывают дополнительные очки команде, а себе оценку: 4-5ответов-4балла-«4»,
6-7 ответов-5 баллов- «5».
На обсуждение заданий 2,3,4,5 геймов дается одна минута. Если ответы досрочные, то эту сэкономленную минуту команда может использовать в обсуждении другого вопроса.
Приложение 2.2
Рефлексивный алгоритм:
"Я", "Мы", "Дело".
"Я" - как чувствовал себя, с каким настроением работал, доволен ли собой.
"Мы" - комфортно ли было работать в малой группе, какие затруднения были в общении.
"Дело" - достиг ли цели учения, какие затруднения возникли, как преодолеть свои учебные проблемы.
-
Стратегия "Insert".
Что знал?
Что узнал нового?
Что удивило?
Чем недоволен?
Рефлексивный алгоритм:
-
Что я узнал нового?
-
Что из этого смогу применить?
-
Что недостаточно узнал?
-
Чем не удовлетворен?
.Набор рефлексивных вопросов:
-
Что показалось Вам сегодня трудным?
-
Каким способом была решена задача, нельзя ли иначе?
-
Что в изученном сегодня для вас самое главное?
-
Какие мысли, прозвучавшие сегодня, созвучны с Вашими?
-
Что показалось неубедительным, с чем Вы не согласны?
-
Какие новые мысли, чувства у вас появились?
-
Были ли моменты радости, удовлетворения от своих удачных ответов?
-
Были ли моменты недовольства собой?
-
Какую пользу Вы извлекли из этого занятия, изученного материала?
-
Почему Вы выбрали именно эти задания?
-
О чем хотелось бы поговорить подробнее?
-
Что бы Вы хотели посоветовать организаторам курса?
-
Заметили ли Вы свои успехи в обучении?
-
Что бы Вы хотели посоветовать организаторам курса?
-
Заметили ли Вы свои успехи в обучении?
Приложение 3
Диагностический инструментарий
Приложение 3.1
Тест по математике на «входе» по классификации уровней усвоения Блума-Кларина.
Вариант 1
Знание
1. Сколько всего сотен в числе 189 000?
А) 1 890
В) 189
С) 18
D) 18 900
2. Укажи верную запись числа шестьдесят четыре тысячи тридцать восемь.