УРОК - ТУРНИР

Урок-турнир

Арифметическая и геометрическая прогрессии.

Цели урока: 1. Обобщение и систематизация теоретического материала по

данной теме.

2. Отработка умений и навыков применения формул n- го члена прогрессии, суммы n-первых членов, свойств членов прогрессии.

3. Развитие познавательной активности учащихся.

4. Формирование интереса к изучению математики.

5. Развитие навыков работы с дополнительной литературой, с историческим материалом.

ХОД УРОКА:

На доске записана тема, команды заняли свои места, учитель настраивает учащихся на урок, формирует цели, поясняет, зачем обобщается и систематизируется материал темы (подготовка к контрольной работе).

Турнир начинается.

1 тур. Представление и приветствие команд, домашнее задание.

Команды готовили выступление из истории прогрессий. Сообщение первой команды.

АРИФМЕТИЧЕСКИЕ ПРОГРЕССИИ В ДРЕВНОСТИ

В клинописных табличках вавилонян, в египетских пирамидах (II в. до н.э.) встречаются примеры арифметических прогрессий. Вот пример задачи из египетского папируса Ахмеса: « Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками, разность же между каждым человеком и его соседом равна меры.» Вот формула которой пользовались египтяне:

а = - (n - 1).

Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и другие. Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским учёным. Ариабхатта (Vв.) применял формулы общего числа, суммы арифметической прогрессии. Но правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении « Книга абака» в 1202 г. ( Леонардо Пезанский)

Вторая команда представляет сценку.

ЗАДАЧА - ЛЕГЕНДА

(Начало нашей эры.)

Индийский царь Шерам позвал к себе изобретателя шахматной игры, своего подданного Сету, чтобы наградить его за остроумную выдумку. Сета издеваясь над царём, потребовал за первую клетку шахматной доски 1 зерно, за вторую- 2 зерна, за третью- 4 зерна и т. д. Обрадованный царь приказал выдать такую «скромную» награду. Однако оказалось, что царь не в состоянии выполнить желание Сеты, так как нужно было выдать количество зёрен, равное сумме геометрической прогрессии 1, 2, 2,2…2.

Её сумма равна 2-1 = 8 446 744 073 709 551 615.

Такое количество зёрен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли.

2 тур. ЗНАТОКИ ПРАВИЛ И ОПРЕДЕЛЕНИЙ

Члены команд по очереди отвечают на теоретические вопросы по данной теме. Каждая команда отвечает на 5 вопросов.

1. Определение арифметической прогрессии. Примеры.

2. Формула n-го члена арифметической прогрессии.

3. Свойство членов арифметической прогрессии.

4. Формула суммы n первых членов арифметической прогрессии.

5. Определение геометрической прогрессии.

6. Свойство членов геометрической прогрессии.

7. Формула n-го члена геометрической прогрессии.

8. Формула суммы n первых членов геометрической прогрессии.

9. Определение бесконечно убывающей геометрической прогрессии.

10. Сумма членов бесконечно убывающей геометрической прогрессии.

Каждая команда может заработать по 5 баллов. В случае, если ученик , которому капитан поручил ответить, не знает ответа на вопрос, отвечает команда, но 0,5 балла команда теряет.

3 тур. ПРОГРЕССИИ В ЖИЗНИ И БЫТУ

Команды решают задачи, приготовленные друг другом. (Максимальная оценка 5 баллов.)

4 тур КОНКУРС КАПИТАНОВ

В это время команды решают за дачи:

1. В арифметической прогрессии 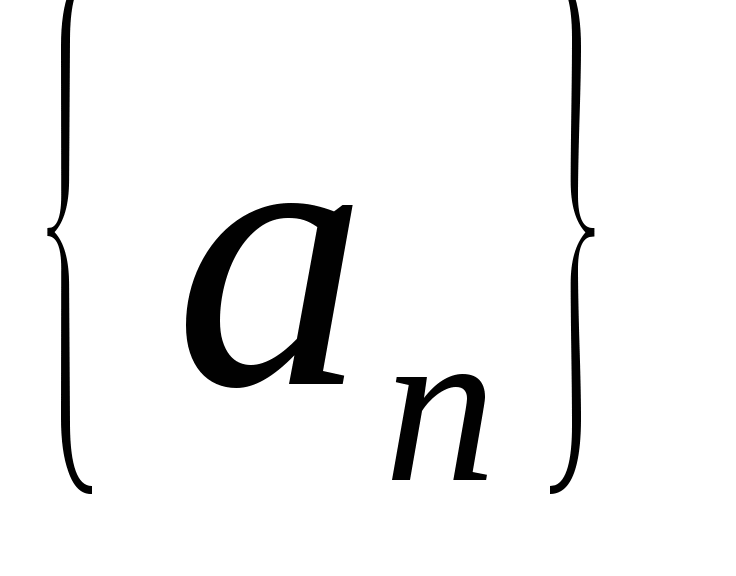: -10;-8;-6;…найдите .

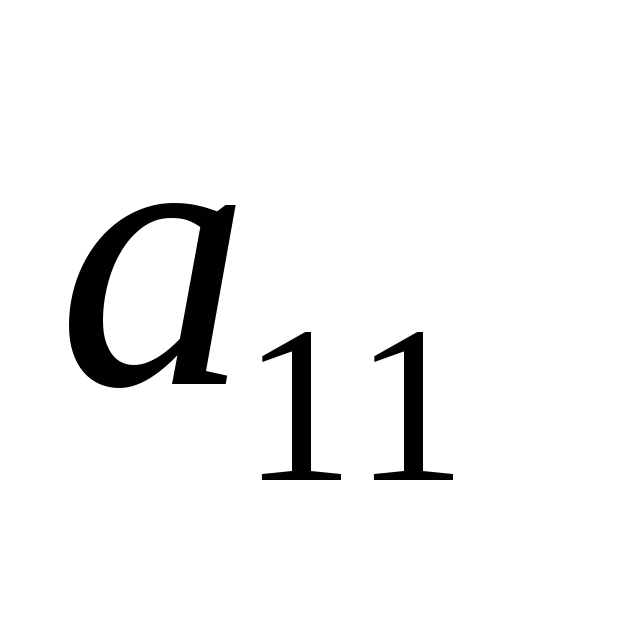2. Найдите четвёртый член геометрической прогрессии 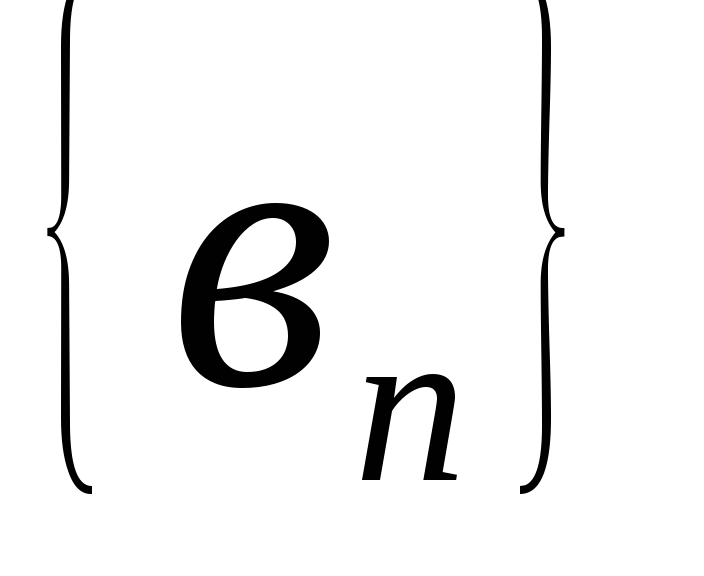, если 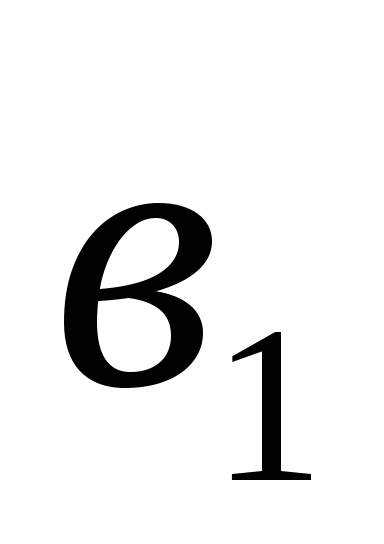= -25,

q = -.

3. Найдите сумму восьми первых членов арифметической прогрессии 10; 6; 2; ...

4. Найдите сумму бесконечно убывающей геометрической прогрессии 12; 3; …

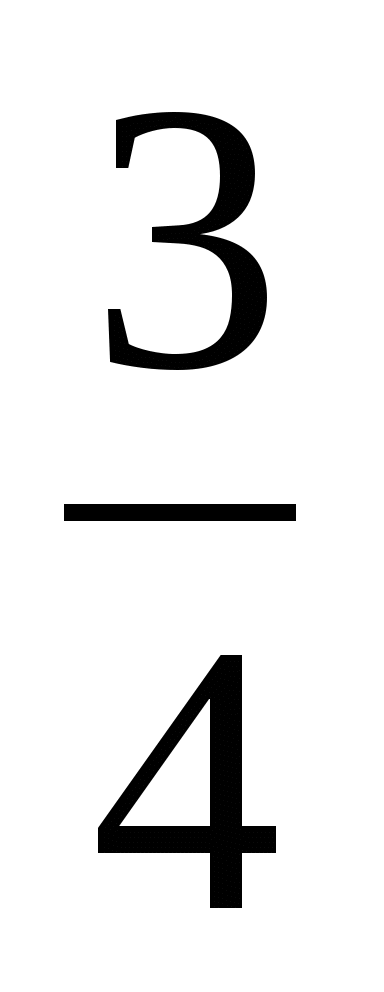5. В геометрической прогрессии 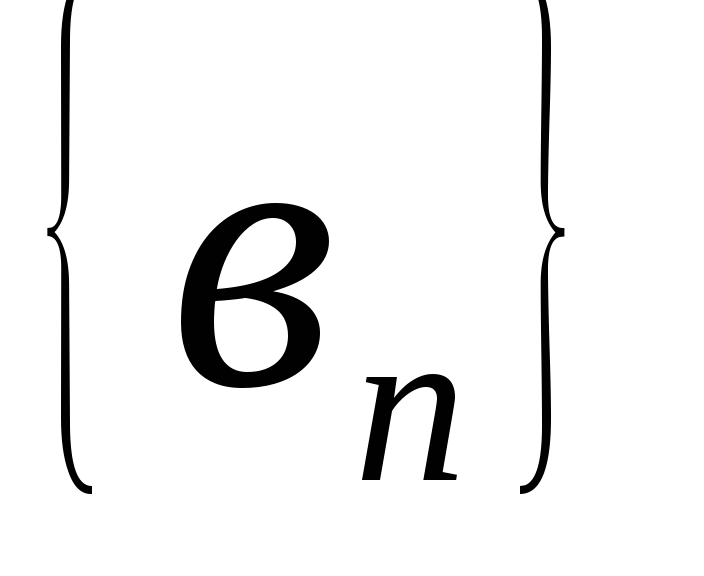: 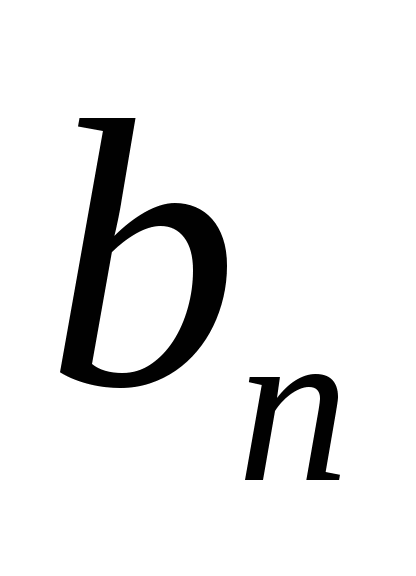=8, 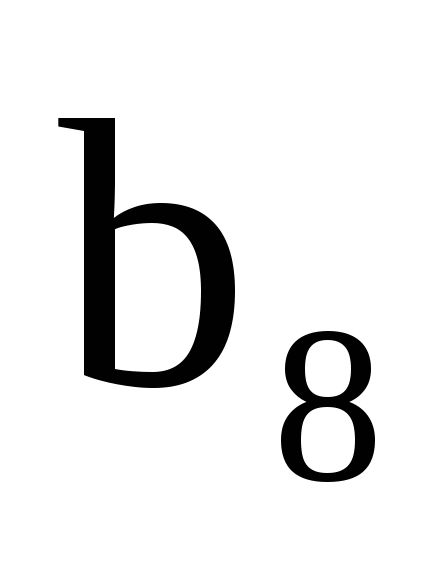=18, q 0. Найдите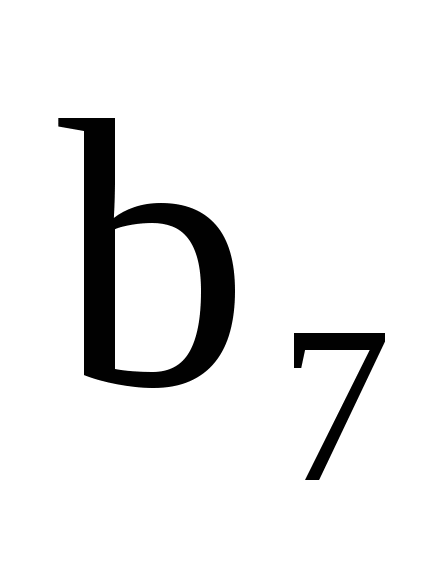

Ответы: 1. 10. 2. . 3. -32. 4. 16. 5. -12.

Капитаны в это время решают задачу: Найдите сумму всех трёхзначных чётных чисел.

Максимальная оценка за тур - 8 баллов (5 баллов получает команда и 3 - капитан).

5 тур БЛИЦ - ТУРНИР

Каждая команда в течении 4 минут должна ответить на большее количество вопросов. За каждый верный ответ - 1 балл. В случае, если команда не знает ответа или не хочет терять времени, команда говорит «Дальше» (по принципу игры «Счастливый случай»).

Вопросы первой команде:

1. - арифметическая прогрессия, =4, d =3. Назовите .

2. - геометрическая прогрессия. Найдите , если =6, q=2.

3. Чему равна сумма первых трёх членов арифметической прогрессии , если =7, =15 ?

4. Дана геометрическая прогрессия , =5, q=. Найдите сумму двух первых членов.

5. Найдите сумму бесконечно убывающей геометрической прогрессии , у которой =4, q=.

6. Если в арифметической прогрессии : =2, d=5, то чему равен 21 её член?

7. В геометрической прогрессии : =3, q=3. Чему равен ?

Вопросы второй команде:

1. -геометрическая прогрессия, =9, q=. Найдите .

2. -арифметическая прогрессия. Найдите , если =5, d=3.

3. В геометрической прогрессии 2; 4; … найдите сумму трёх первых членов.

4. В арифметической прогрессии : =7, =13. Найдите .

5. 3; 1; … бесконечно убывающая геометрическая прогрессия. Найдите её

сумму.

6. В арифметической прогрессии : =10, d=2. Найдите сумму двух первых членов.

7.В геометрической прогрессии : =2,q=3. Найдите .

Подсчитываются баллы каждой команды. Объявляется победитель.

Капитаны оценивают работу каждого ученика, выставляют оценку и комментируют её.