Зачет по теме Производная

10 класс.

Разработал:

учитель математики МБОУ «Краснооктябрьская СОШ»

п. Десятуха Стародубского района Брянской области

Хандус Татьяна Елисеевна.

1. Найдите производную функции в заданной точке x₀.

а) y = (-5x+11)⁴, x₀ = 2.

б) y = 6x - tg x, x₀ = 0.

в) y = , x₀ =.

г) y = 2x + ctg x, x₀ = .

д) y = - √x.

е) y = 2x ³√x + cos²x.

ж) y = -cos² 2x - sin²2x.

з) y = cos 5x cos 3x + sin 5x sin 3x.

и) y = ctg x + , x₀ = .

к) y = , x₀ = .

л) y = 6(2x - 1)².

м) y = .

н) y = √x (2x -4).

о) y = 17.

2.Геометрический смысл производной.

а) Найдите угловой коэффициент касательной, проведённой к графику функции в точке с абсциссой x₀ = , если

f (x) = 2x + ctg x.

б) Угловой коэффициент касательной к графику функции y = f (x) в точке (-2;7), равен 4. Найдите f`(-2).

в) Найдите абсциссу точки графика функции y = x² - 5x +6 , в которой угловой коэффициент касательной равен -4.

г) Найдите тангенс угла наклона касательной, проведённой к графику данной функции через точку с абсциссой x₀ = 2, если f (x) =x³ - ½ x.

д) Касательная в точке М графика функции y= 3x² + 15x +2 параллельна оси абсцисс.

Найдите абсциссу точки М.

е) Прямая, проходящая через начало координат, касается графика функции y = f (x) в точке

C(-6; 12). Найдите f`(-6).

3.Физический смысл производной.

1. Точка движется прямолинейно по закону x(t) = 2t³+ 3t+1. Найдите её ускорение в момент времени t = 3с.

2. Точка движется прямолинейно по закону x(t) = t³- 3t. Найдите её скорость и ускорение в момент времени

t = 1с.

3. Тело движется по закону x(t) = t⁵ + t. Определите x( t ) в момент, когда её скорость 65 м/с.

4. Тело движется по закону x(t) = 3 cos 2t. При каких значениях t ускорение точки положительно?

5. Тело движется по закону x(t) = 3t³- 6t. Найдите ускорение точки в момент, когда её скорость 30 м/с.

6. Тело движется по закону x(t) = 7t + 5t² + t³. Определите скорость точки в момент, когда её ускорение 70 м/с².

7. Тело движется по закону x(t) = -t⁴ - 4t³+ 6t². Определите скорость точки в момент, когда её ускорение максимально.

4.Касательная к графику функции.

1. Прямая y = -3x + 5 параллельна касательной к графику функции y = x² + 6x + 8. Найдите абсциссу точки касания.

2. Прямая y = 5x + 14 параллельна касательной к графику функции y = x³ - 4x² + 9x +14. Найдите абсциссу точки касания.

3. Составьте уравнение касательной к графику функции y = x³ - 2x +1 в точке с абсциссой x₀ =2.

4. Дана кривая y = -x² + 1. Найдите точку её графика, в которой касательная параллельна прямой y = 2x + 3. Написать уравнение касательной.

5. Найдите координаты точки, в которой касательная к графику функции y = x² + √3x -10 образует угол 60° с Оx.

6. Найдите угол между прямой x = 2 и параболой y = x² + 2.

7. Составьте уравнение касательной к графику функции y = в точке пересечения с осью ординат.

8. Составьте уравнение касательной к графику функции y = в точке пересечения с осью абсцисс.

9. На графике функции y = x(x - 4)³. Найти точки, в которых касательные параллельны оси абсцисс.

10. Под каким углом кривая y = sin3x пересекает ось абсцисс в начале координат?

11. В каких точках касательные к кривой y = - x² - x +1 параллельны прямой y = 2x - 1.

12. . Под каким углом к оси Оx наклонена касательная, проведённая к кривой y = x³ - x² - 7x + 6 в точке М₀(2;-4)?

13. Известно, что прямая y = - x - является касательной к линии, заданной уравнением y = 0,5x⁴ - x. Найдите координаты точек касания.

14) Составьте уравнения касательных к кривым y = 2x² - 5 и y = x² -3x + 5, проведённых через точки их пересечения.

</ 15) Найти угол, который образует с осью ординат касательная к кривой y = x⁵ - x³, проведённая в точку с абсциссой x = 1.

5. Применение производной к исследованию функций

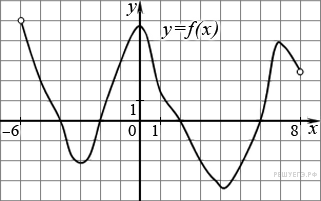
5.1. На рисунке изображен график функции , определенной на интервале (−6; 8).

Определите количество целых точек, в которых производная функции положительна.

5.2. 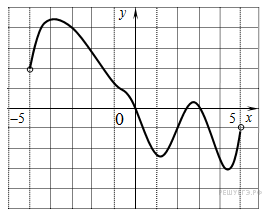На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна.

5.3. 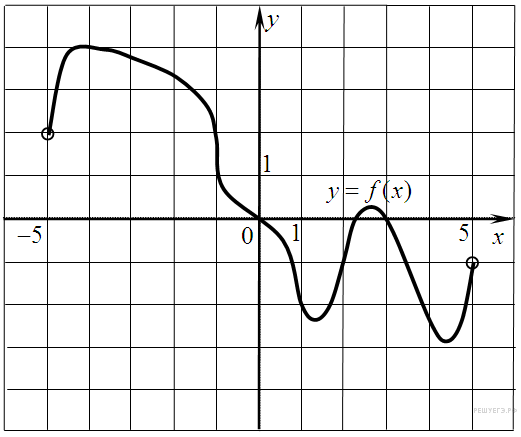На рисунке изображен график функции y=f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямойy = 6 или совпадает с ней.

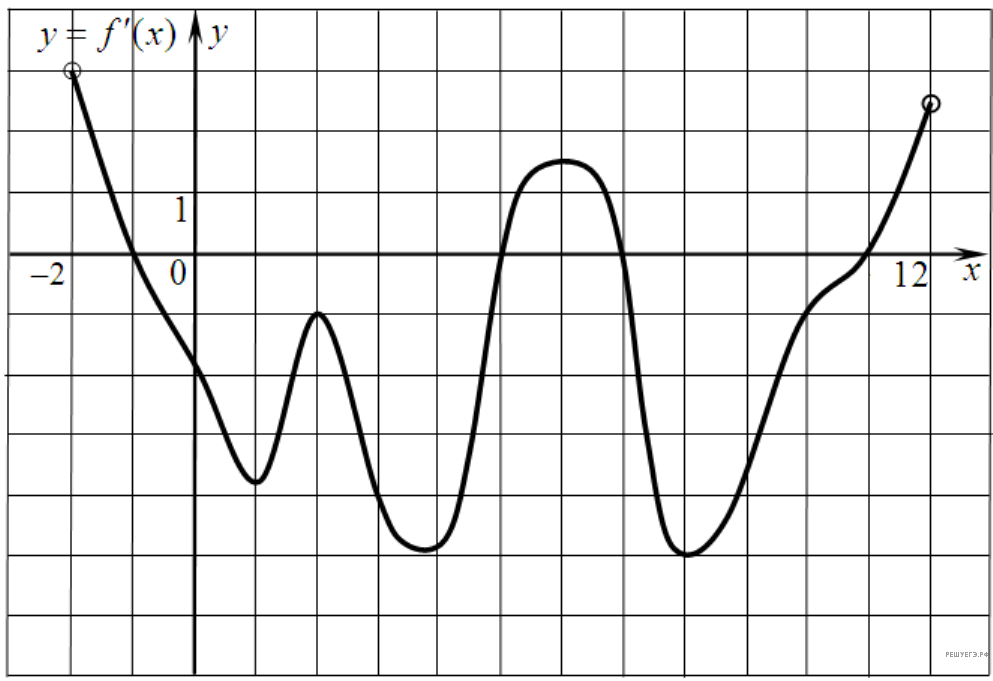
5.4. На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).

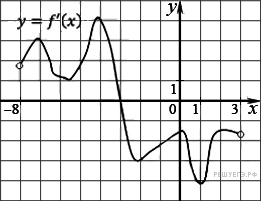
5.5. На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка функция принимает наибольшее значение?

5.6. 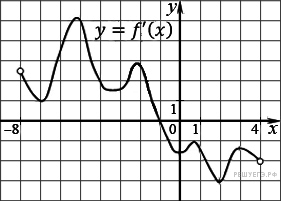На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наименьшее значение?

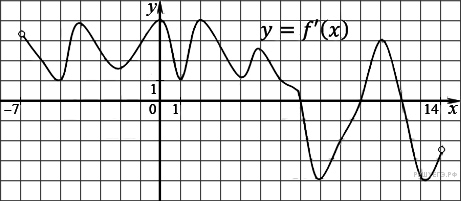
5.7.На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

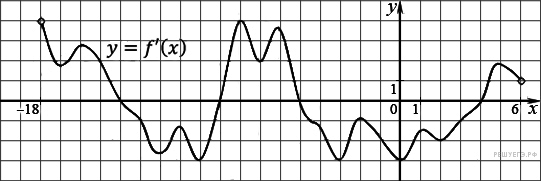
5.8. На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек минимума функции на отрезке .

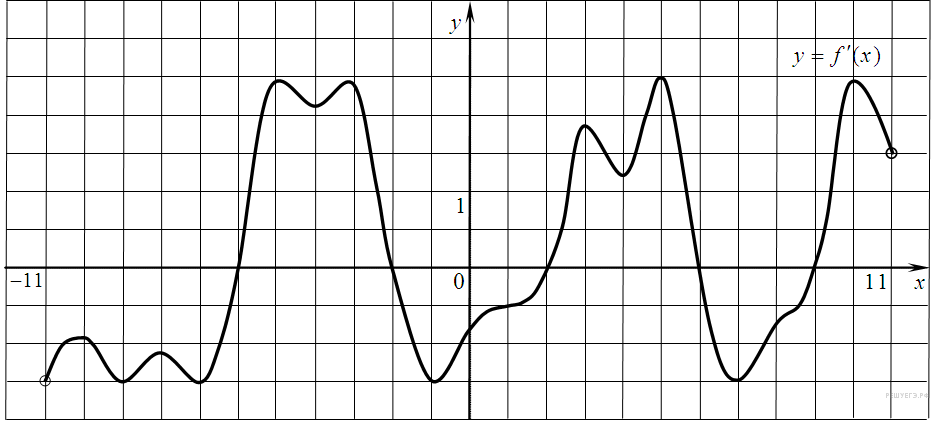
5.9. На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

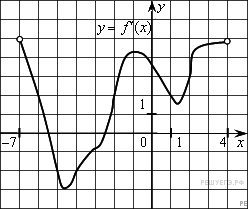
5.10. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

5.11. 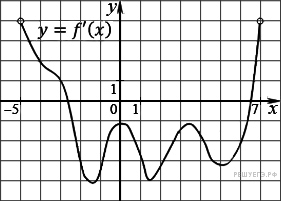На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

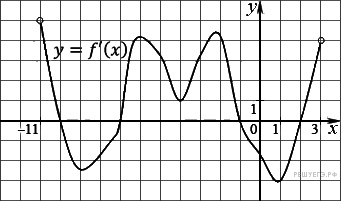
5.12. На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

5.13. На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

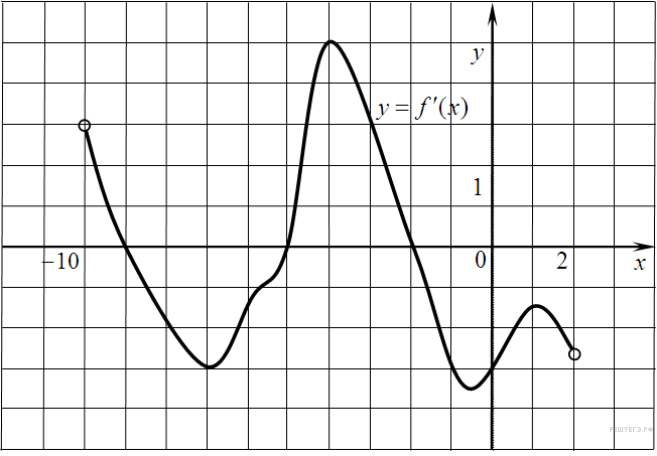
5.14.На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x−11 или совпадает с ней.

5.15. 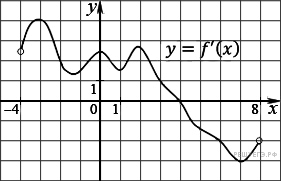На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функцииf(x) на отрезке [−2; 6].

5.16. На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.

5.17.На рисунке изображён график производной функции и восемь точек на оси абсцисс: , . В скольких из этих точек функция возрастает?

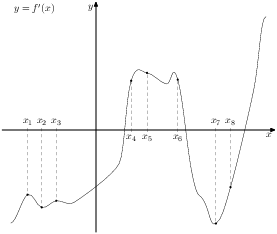
5.18.На рисунке изображён график производной функции и восемь точек на оси абсцисс: ,. В скольких из этих точек функция убывает?

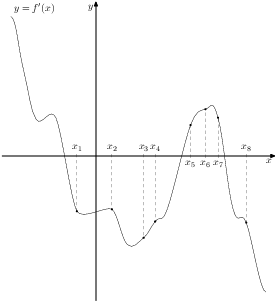
5.19. На рисунке изображен график функции и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

5.20.

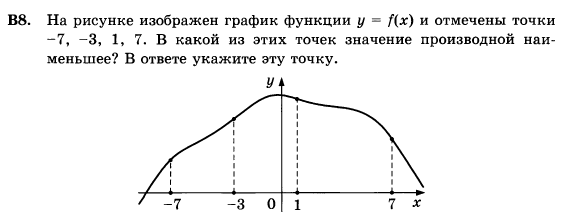
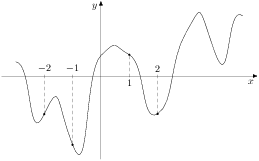
5.21. На рисунке изображен график функции и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.