Разработка урока по теме Разложение вектора по двум неколлинеарным векторам. Координаты вектора».

Геометрия - 9 класс Урок № 11

Тема: «Разложение вектора по двум неколлинеарным векторам. Координаты вектора».

Цель: Создать условия для формирования умения раскладывать вектор по двум неколлинеарным векторам, ввести понятие координат вектора и рассмотреть правила действий над векторами с заданными координатами.

Задачи:

- развитие познавательной активности

-формирование умения раскладывать вектор по двум неколлинеарным векторам

- формировать умения находить координаты вектора и выполнять действия над векторами, заданными координатами

-развивать умение работать с текстовой, символьной информацией

-воспитывать интерес к изучению математических дисциплин

Планируемые результаты:

Личностные: положительная мотивация к обучению, умение преодолевать трудности, успешность каждого в открытии нового, активность, внимание

Предметные: формирование умения раскладывать вектор по двум неколлинеарным векторам, доказывать теорему о разложении вектора, решать задачи разными способами, осуществлять выбор оптимального решения; формировать умение определять координаты вектора, выполнять операции с векторами с заданными координатами; формирование графической культуры; оперирование правилами сложения и вычитания векторов, умножения вектора на число, понятиями: абсолютная величина, вектор, коллинеарные векторы, равные векторы

Метапредметные:

Познавательные: развитие логического и образного мышления, умение анализировать, делать выводы, проводить сравнение; формирование грамотного употребления математической терминологии в устной речи.

Коммуникативные: развитие умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, продуктивное взаимодействие и сотрудничество со сверстниками

Регулятивные: освоение действий по проверке, анализу и коррекции результатов своей деятельности; осознание качества и уровня усвоения; правильность выполнения учебной задачи

Оборудование: мультимедийный проектор, компьютер, текстовая информация, учебник.

Ход урока.

1. Организационный момент.

Сообщение темы и целей урока. Отчет старосты об отсутствующих.

2. Актуализация знаний и умений обучающихся.

1. Анализ контрольной работы. Разбор нерешенных заданий. Выявление типичных ошибок обучающихся.

2. Систематизация теоретического материала.

Устный опрос

1. Дайте определение вектора

[Вектором или направленным отрезком называется отрезок для которого указано, какая из его граничных точек считается началом, а какая - концом.]

2 Длина или модуль ненулевого вектора АВ - это

[длина отрезка АВ]

3.Ненулевые вектора называются коллинеарными, если…

[они лежат либо на одной прямой, либо на параллельных прямых]

4.Сколько векторов равных данному можно отложить от точки

[один]

5. Два коллинеарных вектора направленные одинаково называются

[сонаправлеными]

6. Векторы называются равными, если…

[они сонаправлены и их длины равны]

3. Изучение нового материала.

Разложение вектора по двум неколлинеарным векторам.

При решении задач часто возникает необходимость выразить какой-либо вектор через уже заданные векторы. Такая операция называется разложением вектора по неколлинеарным векторам.

Лемма о коллинеарных векторах.

Лемма - это вспомогательное утверждение, с помощью которого доказывается следующая теорема или несколько теорем.

Теорема: Если векторы и коллинеарны и ā≠ō, то существует такое число k, что = k.

Так как рассматриваемые векторы, по условию коллинеарны, то они могут иметь одинаковые направления. Рассмотрим два случая, когда векторы и сонаправлены и противоположно направлены.

Доказательство:

1) . Возьмем число . Так как k≥ 0, то векторы k и сонаправлены (рисунок 1). Кроме того, их длины равны: │kā│=│k│*│ā│= = *│ā│=││. Поэтому = k

2) . Возьмем число . Так как k<0, то векторы k и снова сонаправлены (рисунок2). Их длины также равны: |k|=|k|*||= *||=||. Поэтому = k

Рис. 2

3. Теорема о разложении вектора по двум неколлинеарным векторам.

Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Пусть и - данные неколлинеарные векторы, вектор представлен в виде

= х+у, где х и у - некоторые числа. Принято говорить, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения.

Доказательство:

Возможны два случая:

1) Вектор коллинеарен одному из векторов и , например, вектору (рисунок1). В этом случае по лемме о неколлинеарных векторах вектор можно представить в виде = у, где у - некоторое число, и, следовательно, =0+у, т.е. вектор разложении по векторам

и .

2) Вектор не коллинеарен ни вектору , ни вектору . Отметим какую-нибудь точку О и отложим от нее векторы = , =, = (рис. 2).

Через точку Р проведем прямую, параллельную прямой ОВ, и обозначим через А₁ точку пересечения этой прямой с прямой ОА. По правилу треугольника = + . Но векторы и коллинеарны соответственно векторам и , поэтому существует числа х и у, такие, что = х, = у. Следовательно, = х+у, т.е. вектор разложен по векторам и .

Докажем теперь, что коэффициенты х и у разложения определяются единственным образом. Допустим, что наряду с разложением = х+у имеет место другое разложение = х₁+у₁. Вычитая второе равенство из первого и используя правила действий над векторами, получаем =(х-х₁) + (у-у₁) . Это равенство может выполняться только в том случае, когда коэффициенты х-х₁ и у-у₁ равны нулю. В самом деле, если предположить, например, что х-х₁ ≠0, то из полученного равенства найдем = -, а значит векторы и коллинеарны. Но это противоречит условию теоремы. Следовательно, х-х₁=0 и у-у₁=0, откуда х=х₁ и у=у₁. Это и означает, что коэффициенты вектора определяются единственным образом. Теорема доказана.

Координаты вектора.

Рассмотрим прямоугольную систему координат. Отложим от начала координат О единичные векторы (т.е. векторы, длины которых равны единице) i и j так, чтобы направление вектора i совпало с направлением оси Ох, а направление вектора j - с направлением оси Oy. Векторы i и j назовем координатными векторами.

</ Координатные векторы неколлинеарны, поэтому любой вектор р можно разложить по координатным векторам , т.е. представить в виде p = xi + yj, причём коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора р по координатным векторам называются координатами вектора р в данной системе координат. Координатные векторы будем записывать в фигурных скобках после обозначения вектора. На рисунке вектор , и вектор .

Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.

и - данные векторы

1) ;

2) ;

3) .

4. Формирование знаний и умений обучающихся.

1. Решить задачи № 911 (а).

2. Решить задачи № 915 (по готовому чертежу) и № 916 (а).

3. Решить задачу № 917 на доске и в тетрадях.

4. Устно решить задачи № 922-925, используя правила, записанные в тетрадях.

5. Записать утверждение задачи № 927 без доказательства:

1) Если два вектора коллинеарные, то координаты одного вектора пропорциональны координатам другого: если коллинеарен вектору , то x1 : x2 = y1 : y2.

2) Если координаты одного вектора пропорциональны координатам другого вектора, то эти векторы коллинеарные.

6. Решить задачу № 928.

Решение

Используем условие коллинеарности векторов: .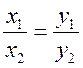

1) (3; 7) и (6; 14), так как ;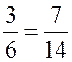

2) (-2; 1) и (2; -1), так как .

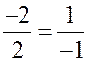5. Подведение итогов урока.

Выводы по теме:

1.Лемма - это вспомогательное утверждение, употребляемое при доказательстве одной или нескольких теорем.

2. Лемма (о коллинеарных векторах). Если векторы и коллинеарны и вектор ¹0, то существует такое число k, при котором = k

3. Пусть и - данные неколлинеарные векторы, вектор представлен в виде

= х+у, где х и у - некоторые числа. Принято говорить, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения.

4. Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

5. Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.

и - данные векторы

1) ;

2) ;

3) .

6. Домашнее задание: прочитать п. 86 - 87, выполнить № 912 (д - и), № 915

9