Урок+презентация по геометрии на тему 'Теорема Пифагора'

Урок геометрии в 8 классе

по теме: «Теорема Пифагора».

(2 урока)

Тип урока: проблемный урок по изучению нового материала.

Оборудование урока: 1. Компьютер.

2. Мультимедиапроектор.

3. Интерактивная доска.

Цели урока: 1.Познакомиться с теоремой Пифагора.

2.Доказать теорему Пифагора.

3.Показать её применение в ходе решения задач.

4.Развивать логическое мышление учащихся.

5.Повышать интерес к знаниям.

Ход урока

Комментарии к уроку

Учитель предлагает решить задачи, условия задач представлены в презентации. (Слайд 1,2)

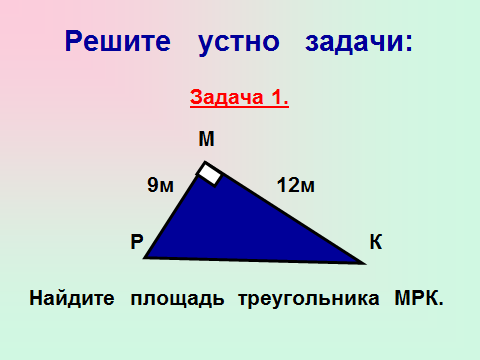
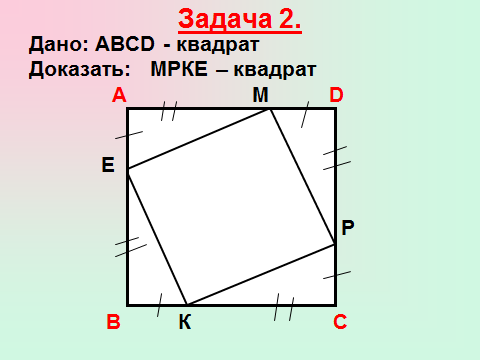
Актуализация предыдущего опыта, создание ситуации успеха.

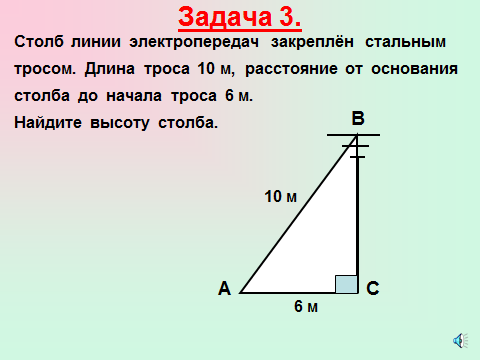
Учащимся предлагается задача с практическим содержанием, решить которую они не могут. (Слайд 3)

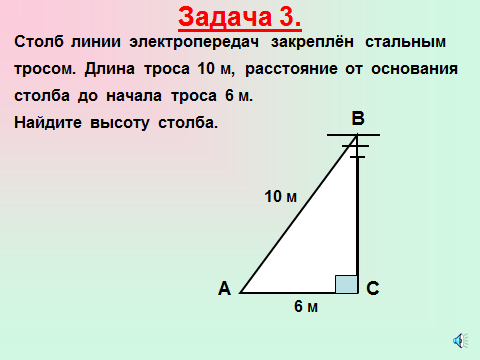
Создаётся проблемная ситуация.

Учащиеся сталкиваются с затруднением.

Учащиеся выдвигают свои гипотезы по решению данной задачи. Ведут поиск её решения совместно с учителем. Ученики делают вывод о том, что нужно знать какое-то соотношение между катетами и гипотенузой в прямоугольном треугольнике.

Слайды 4 и 5.

Учитель объявляет тему и цели урока, сообщает план урока.

Сообщает о Пифагоре один из учеников класса.(текст сообщения приведён в Приложении 1).

Портрет Пифагора демонстрируется учащимся на слайде 6

Учащиеся слушают, заранее подготовленное сообщение о Пифагоре Самосском.

Выполняется практическое задание каждым учащимся в рабочих тетрадях. (Слайд 7.)

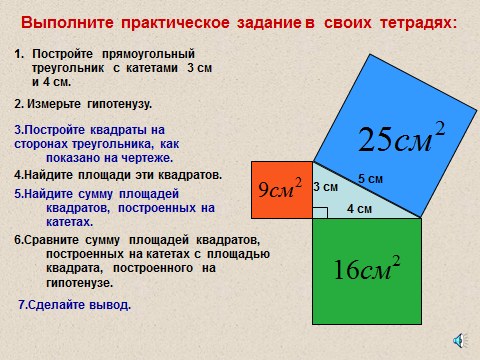
Учащимся предлагается практическое доказательство теоремы Пифагора для треугольника с катетами 3 и 4 см и гипотенузой 5см. Учащиеся делают вывод по данной задаче. (Слайд 8)

Учитель интересуется , а справедливо ли полученное утверждение для любого прямоугольного треугольника?

Учащиеся предполагают, что да.

Формулируется теорема Пифагора и записывается в тетрадь. (Слайд 9)

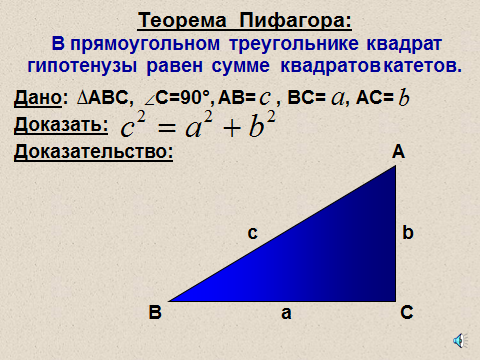
Доказательство теоремы Пифагора учащиеся изучают самостоятельно и записывают в тетрадь с печатной основой на странице 58. ( Рогулева А.В. Геометрия 8 класс, Рабочая тетрадь: Саратов, Лицей, 2007).

Один из учащихся, по желанию, доказывает теорему Пифагора у доски.

Учитель задаёт вопрос: Можно ли теорему Пифагора сформулировать так?

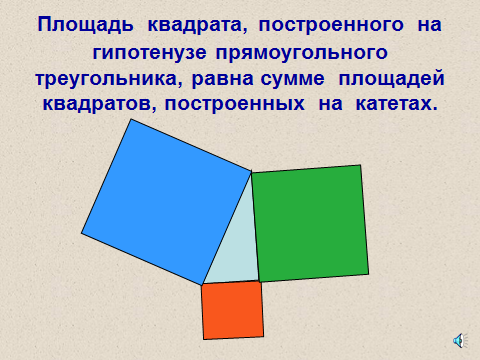
Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах. (Слайд 10)

Обсуждается эквивалентность трёх формулировок теоремы Пифагора.

Идёт обобщение ответов учащихся.

Теорема Пифагора - теорема бабочки, невесты, быка. Учащимся сообщается данная информация и предлагается дома найти ответы на поставленные вопросы.

Учащимся предлагается в тетрадях и на интерактивной доске выполнить задание. (Слайд 11)

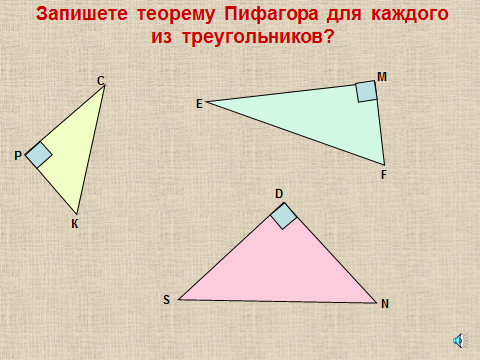
Теорема Пифагора используется для записи соответствующих равенств.

Учитель акцентирует внимание учащихся на умении найти гипотенузу и катеты, независимо от расположения прямоугольного треугольника.

В рабочих тетрадях и на интерактивной доске решаются задачи по готовым чертежам. (Слайд 12)

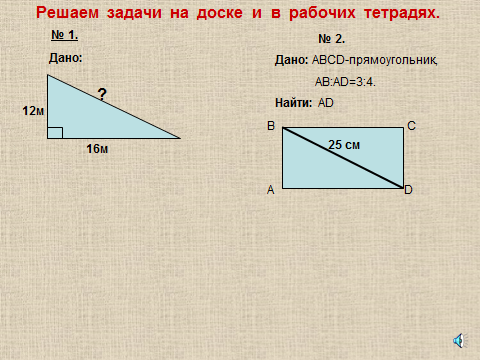
Отрабатываются навыки использования теоремы Пифагора.

Из учебника решаются задачи.

Страница 132 № 487, 493 (Слайд 13)

Задача №487 решается с последующей проверкой полного решения.

(Слайд 14).

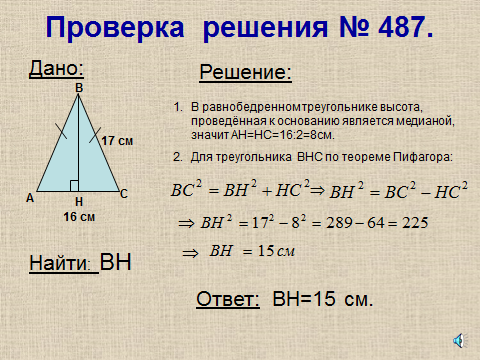
А в задаче №493 проверяется ответ.

Учитель возвращает учащихся к задаче с практическим содержанием. (Слайд 3)

Происходит устное решение данной проблемной задачи.

Учащимся предлагается выполнить самостоятельную работу по готовым чертежам в течение 5-7 мин. (Слайд 15)

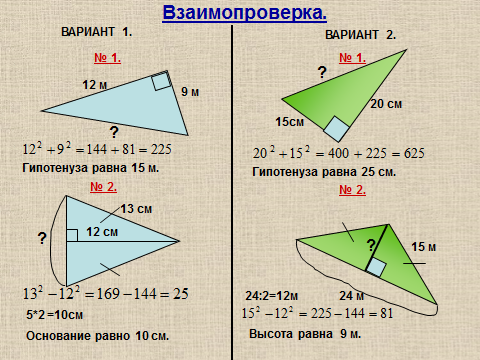
После выполнения самостоятельной работы учащиеся обмениваются работами и происходит взаимопроверка с помощью

Слайда 16.

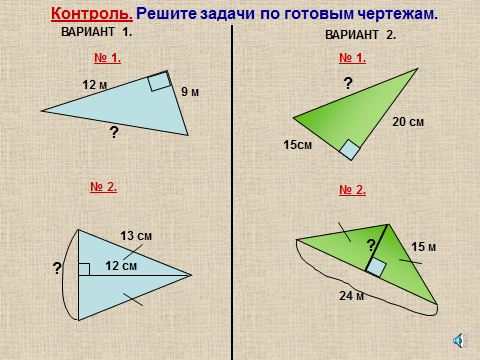
Учащиеся подчёркивают неверные решения и сдают работы учителю.

Домашнее задание даётся дифференцированное. (Слайд 17)

Учитель даёт соответствующие пояснения к выполнению домашнего задания.

Учитель:

Какое значение имеет для вас сегодняшний урок?

Что нового вы узнали на уроке?

Чему научились?

Подводятся итоги. Наиболее активные учащиеся получают оценки.

Литература,

используемая для подготовки к уроку:

1.Л.С.Атанасян, В.Ф. Бутузов и др. Геометрия 7-9, учебник для общеобразовательных учреждений. М.:Просвещение,2007.

2.Л.С. Атанасян, Дополнительные главы к учебнику геометрии 8 класс, 2005.

3.Рогулева А.В., Геометрия. 8 класс. Рабочая тетрадь: В 2ч.-Саратов: Лицей, 2007.

4.Гаврилова Н.Ф. Поурочные разработки по геометрии 8 класс. -М.:ВАКО,2005.

Приложение 1.

ПИФАГОР

В VI веке до нашей эры средоточием греческой науки и искусства стала Иония - группа островов Эгейского моря, расположенных у берегов Малой Азии. Там в семье золотых дел мастера, резчика печатей и гравера Мнесарха родился сын. По преданию, в Дельфах, куда приехали Мнесарх с женой Парфенисой, - то ли по делам, то ли в свадебное путешествие - оракул предрек им рождение сына, который прославится в веках своей мудростью, делами и красотой. Бог Аполлон, устами оракула, советует им плыть в Сирию. Пророчество чудесным образом сбывается - в Сидоне Парфениса родила мальчика. И тогда по древней традиции Парфениса принимает имя Пифиада, в честь Аполлона Пифийского, а сына нарекает Пифагором, то есть предсказанным пифией.

В легенде ничего не говорится о годе рождения Пифагора; исторические исследования датируют его появление на свет приблизительно 580 г. до н. э. Вернувшись из путешествия, счастливый отец воздвигает алтарь Аполлону и окружает юного Пифагора заботами, которые могли бы способствовать исполнению божественного пророчества.

Возможности дать сыну хорошее воспитание и образование у Мнесарха были. Как всякий отец, Мнесарх мечтал, что сын будет продолжать его дело - ремесло золотых дел мастера. Жизнь рассудила иначе. Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам. У своего первого учителя Гермодамаса Пифагор получает знания основ музыки и живописи. Для упражнения памяти Гермодамас заставлял его учить песни из «Одиссеи» и «Илиады». Первый учитель прививал юному Пифагору любовь к природе и ее тайнам. «Есть еще другая Школа, - говорил Гермодамас, - твои чувствования происходят от Природы, да будет она первым и главным предметом твоего учения».

Прошло несколько лет, и по совету своего учителя Пифагор решает продолжить образование в Египте, у жрецов. Попасть в Египет в то время было трудно, потому что страну фактически закрыли для греков. Да и властитель Самоса тиран Поликрат тоже не поощрял подобные поездки. При помощи учителя Пифагору удается покинуть остров Самос. Но пока до Египта далеко. Он живет на острове Лесбос у своего родственника Зоила. Там происходит знакомство Пифагора с философом Ферекидом - другом Фалеса Милетского. У Ферекида Пифагор учится астрологии, предсказанию затмений, тайнам чисел, медицине и другим обязательным для того времени наукам. Пифагор прожил на Лесбосе несколько лет. Оттуда путь Пифагора лежит в Милет - к знаменитому Фалесу, основателю первой в истории философской школы. От него принято вести историю греческой философии.

Пифагор внимательно слушает в Милете лекции Фалеса, тогда уже восьмидесятилетнего старца, и его более молодого коллегу и ученика Анаксимандра, выдающегося географа и астронома. Много важных знаний приобрел Пифагор за время своего пребывания в Милетской школе. Но Фалес тоже советует ему поехать в Египет, чтобы продолжить образование. И Пифагор отправляется в путь.

Перед Египтом он на некоторое время останавливается в Финикии, где, по преданию, учится у знаменитых сидонских жрецов. Пока он живет в Финикии, его друзья добиваются того, что Поликрат - властитель Самоса, не только прощает беглеца, но даже посылает ему рекомендательное письмо для Амазиса - фараона Египта. В Египте благодаря покровительству Амазиса Пифагор знакомится с мемфисскими жрецами. Ему удается проникнуть в «святая святых» - египетские храмы, куда чужестранцы не допускались. Чтобы приобщиться к тайнам египетских храмов, Пифагор, следуя традиции, принимает посвящение в сан жреца.

Учеба Пифагора в Египте способствует тому, что он сделался одним из самых образованных людей своего времени. К этому периоду относится событие, изменившее его дальнейшую жизнь. Скончался фараон Амазис, а его преемник по трону не выплатил ежегодную дань Камбизу, персидскому Царю, что послужило достаточным поводом для войны. Персы не пощадили даже священные храмы. Подверглись гонениям и жрецы: их убивали или брали в плен. Так попал в персидский плен и Пифагор.

Согласно старинным легендам, в плену в Вавилоне Пифагор встречался с персидскими магами, приобщился к восточной астрологии и мистике, познакомился с учением халдейских мудрецов. Халдеи познакомили Пифагора со знаниями, накопленными восточными народами в течение многих веков: астрономией и астрологией, медициной и арифметикой. Эти науки у халдеев в значительной степени опирались на представления о магических и сверхъестественных силах, они придали определенное мистическое звучаний философии и математике Пифагора.

Двенадцать лет пробыл в вавилонском плену Пифагор, пока его не освободил персидский царь Дарий Гистасп, прослышавший о знаменитом греке. Пифагору уже шестьдесят, он решает вернуться на родину, чтобы приобщить к накопленным знаниям свой народ.

С тех пор как Пифагор покинул Грецию, там произошли большие изменения. Лучшие умы, спасаясь от персидского ига, перебрались в Южную Италию, которую тогда называли Великой Грецией, и основали там города-колонии Сиракузы, Агригент, Кротон. Здесь и задумывает Пифагор создать собственную философскую школу.

Довольно быстро он завоевывает большую популярность среди жителей. Энтузиазм населения так велик, что даже девушки и женщины нарушали закон, запрещавший им присутствовать на собраниях. Одна из таких нарушительниц, девушка по имени Теано, становится вскоре женой Пифагора.

В это время в Кротоне и других городах Великой Греции растет общественное неравенство; вошедшая в легенды роскошь сибаритов (жителей города Сибариса) бок о бок соседствует с бедностью, усиливается социальная угнетенность, заметно падает нравственность. Вот в такой обстановке Пифагор выступает с развернутой проповедью нравственного совершенствования и познания. Жители Кротона единодушно избирают мудрого старца цензором нравов, своеобразным духовным отцом города. Пифагор умело использует знания, полученные в странствиях по свету. Он объединяет лучшее из разных религий и верований, создает свою собственную систему, определяющим тезисом которой стало убеждение в нерасторжимой взаимосвязи всего сущего (природы, человека, космоса) и в равенстве всех людей перед лицом вечности и природы.

В совершенстве владея методами египетских жрецов, Пифагор «очищал души своих слушателей, изгонял пороки из сердца и наполнял умы светлой истиной». В так называемых «Золотых стихах» Пифагор выразил те нравственные правила, строгое исполнение которых приводит души заблудших к совершенству. Вот некоторые из них: не делай никогда того, чего ты не знаешь, но научись всему, что следует знать, и тогда ты будешь вести спокойную жизнь; переноси кротко свой жребий, каков он есть, и не ропщи на него; приучайся жить без роскоши.

Со временем Пифагор прекращает выступления в храмах и на улицах, а учит уже в своем доме. Система обучения была сложной, многолетней. Желающие приобщиться к знанию должны пройти испытательный срок от трех до пяти лет. Все это время ученики обязаны хранить молчание и только слушать Учителя, не задавая никаких вопросов. В этот период проверялись их терпение, скромность, Пифагор учил медицине, принципам политической деятельности, астрономии, математике, музыке, этике и многому другому. Из его школы вышли выдающиеся политические и государственные деятели, историки, математики и астрономы. Это был не только учитель, но и исследователь. Исследователями становились и его ученики. Пифагор развил теорию музыки и акустики, создав знаменитую «пифагорейскую гамму» и, проведя основополагающие эксперименты по изучению музыкальных тонов: найденные соотношения он выразил на языке математики. В Школе Пифагора впервые высказана догадка о шарообразности Земли. Мысль о том, что движение небесных тел подчиняется определенным математическим соотношениям, идеи «гармонии мира» и «музыки сфер», впоследствии приведшие к революции в астрономии, впервые появились именно в Школе Пифагора.

Многое сделал ученый и в геометрии. Доказанная Пифагором знаменитая теорема, носит его имя. Достаточно глубоко исследовал Пифагор и математические отношения, закладывая тем самым основы теории пропорций. Особенное внимание он уделял числам и их свойствам, стремясь познать смысл и природу вещей. Посредством чисел он пытался даже осмыслить такие вечные категории бытия, как справедливость, смерть, постоянство, мужчина, женщина и прочее.

Пифагорейцы полагали, что все тела состоят из мельчайших частиц - «единиц бытия», которые в различных сочетаниях соответствуют различным геометрическим фигурам. Число для Пифагора было и материей, и формой Вселенной. Из этого представления вытекал и основной тезис пифагорейцев: «Все вещи - суть числа». Но поскольку числа выражали «сущность» всего, то и объяснять явления природы следовало только с их помощью. Пифагор и его последователи своими работами заложили основу очень важной области математики - теории чисел.

Все числа пифагорейцы разделяли на две категории - четные и нечетные, что характерно и для некоторых других древних цивилизаций. Позднее выяснилось, что пифагорейские «четное - нечетное», «правое - левое» имеют глубокие и интересные следствия в кристаллах кварца, в структуре вирусов и ДНК, в знаменитых опытах Пастера с поляризацией винной кислоты, в нарушении четности элементарных частиц и других теориях.

Не чужда была пифагорейцам и геометрическая интерпретация чисел. Они считали, что точка имеет одно измерение, линия - два, плоскость - три, объем - четыре измерения. Десятка, может быть выражена суммой первых четырех чисел (1+2+3+4=10), где единица - выражение точки, двойка - линии и одномерного образа, тройка - плоскости и двумерного образа, четверка - пирамиды, то есть трехмерного образа. Ну, и чем не четырехмерная Вселенная Эйнштейна?

При суммировании всех плоских геометрических фигур - точки, линии и плоскости - пифагорейцы получали совершенную, божественную шестерку.

Справедливость и равенство пифагорейцы видели в квадрате числа. Символом постоянства у них было число девять, поскольку все кратные девяти имеют сумму цифр опять-таки девять. Число восемь у пифагорейцев символизировало смерть, так как кратные восьми имеют уменьшающуюся сумму цифр.

Пифагорейцы считали четные числа женскими, а нечетные - мужскими. Нечетное число - оплодотворяющее, и, если его сочетать с четным, оно возобладает; кроме того, если разлагать четное и нечетное надвое, то четное, как женщина, оставляет в промежутке пустое место, между двумя частями. Поэтому и считают, что одно число свойственно женщине, а другое мужчине. Символ брака у пифагорейцев состоял из суммы мужского, нечетного числа три и женского, четного числа два. Брак - это пятерка, равная трем плюс два. По той же причине прямоугольный треугольник со сторонами три, четыре, пять был назван ими «фигура невесты».

Четыре числа, составляющие тетраду, - один, два, три, четыре - имеют прямое отношение к музыке: они задают все известные консонантные интервалы - октаву (1:2), квинту (2:3) и кварту (3:4). Иными словами, декада воплощает не только геометрически-пространственную, но и музыкально-гармоническую полноту космоса. Среди свойств десятки отметим еще и то, что в нее входит равное количество простых и составных чисел, а также столько же четных, сколько и нечетных.

Сумма чисел, входящих в тетраду, равна десяти, именно поэтому десятка считалась у пифагорейцев идеальным числом и символизировала Вселенную. Поскольку число десять - идеальное, рассуждали они, на небе должно быть ровно десять планет. Надо заметить, что тогда были известны лишь Солнце, Земля и пять планет.

Знаменитая тетрада, состоящая из четырех чисел, повлияла через пифагорейцев на Платона, который придавал особое значение четырем материальным элементам: земле, воздуху, огню и воде. Пифагорейцы знали также совершенные и дружественные числа. Совершенным называлось число, равное сумме своих делителей. Дружественные - числа, каждое из которых - сумма собственных делителей другого числа. В древности числа такого рода символизировали дружбу, отсюда и название.

Кроме чисел, вызывавших восхищение и преклонение, у пифагорейцев были и так называемые «нехорошие» числа. Это числа, которые не обладали никакими достоинствами, а еще хуже, если такое число было окружено «хорошими» числами. Примером тому может служить знаменитое число тринадцать - чертова дюжина или число семнадцать, вызывавшее особое отвращение у пифагорейцев.

Попытку Пифагора и его школы связать реальный мир с числовыми отношениями нельзя считать неудачной, поскольку в процессе изучения природы пифагорейцы наряду с робкими, наивными и порой фантастическими представлениями выдвинули и рациональные способы познания тайн Вселенной. Сведение астрономии и музыки к числу дало возможность более поздним поколениям ученых понять мир еще глубже.

После смерти Пифагора в Метапонте (Южная Италия), куда он бежал после восстания в Кротоне, его ученики обосновались в разных городах Великой Греции и организовали там пифагорейские общества.

В новое время, особенно благодаря бурному развитию естествознания, астрономии и математики, идеи Пифагора о мировой гармонии приобретают новых поклонников. Великие Коперник и Кеплер, знаменитый художник и геометр Дюрер, гениальный Леонардо да Винчи, английский астроном Эддингтон, экспериментально подтвердивший в 1919 г. теорию относительности, и многие другие ученые и философы продолжают находить в научно-философском наследии Пифагора необходимое основание для установления закономерностей нашего мира.