Конспект урока на тему 'Сечения' (10 класс)

Тема 2. Параллельность прямых и плоскостей в пространстве (21 час).

УРОК № 4. Аксиомы стереометрии. Взаимное расположение пр-х в простр-ве (10 ч).

Тема. Сечения.

Цели урока: формирование у учащихся умений построения сечений тетраэдра и параллелепипеда различными плоскостями; закрепление алгоритма построения сечений и отработка навыков построения сечений многогранников.

Ход урока.

1. Организационный момент. Проверка домашнего задания.

2. Актуализация опорных знаний.

1. Опрос по теории и решение задач устно.

1. Сформулировать аксиомы стереометрии.

2. Сформулировать следствия из аксиом стереометрии.

3. Объяснение нового материала.

Построить сечение означает начертить многоугольник в плоскости сечения, по которому эта плоскость пересекает грани многогранника.

Используем метод следов.

Следом сечения на указанной плоскости называется прямая пересечения этой плоскости с плоскостью сечения.

Основные правила построения сечений

1. Если даны (или уже построены) две точки плоскости сечения на одной грани многогранника, то след сечения в этой плоскости - прямая, проходящая через эти точки.

2. Если дана (или уже построена) прямая пересечения плоскости сечения с основанием многогранника (след на основании) и есть точка, принадлежащая определенной боковой грани, то нужно определить точку пересечения данного следа с этой боковой гранью.

3. Точку пересечения плоскости сечения с основанием можно определить как точку пересечения какой-либо прямой в плоскости сечения с ее проекцией на плоскость основания.

Алгоритм построения сечений многогранников:

а) определить грани, с которыми секущая плоскость имеет две общие точки, и провести через данные точки прямые;

б) определить грани, с которыми секущая плоскость имеет одну общую точку, построить вторую общую точку и провести через них прямую;

в) определить грани, с которыми секущая плоскость не имеет общих точек, построить две общие точки, и провести через них прямую;

г) выделить отрезки прямых, по которым секущая плоскость пересекает ребра многогранника, заштриховать полученный многоугольник.

Задача 1. Построить сечение тетраэдра плоскостью, проходящей через данные точки D, Е, K.

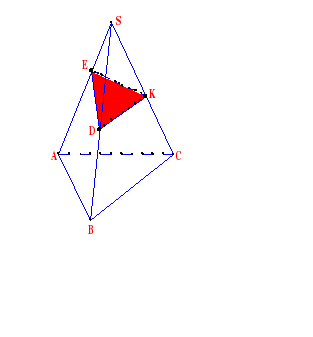
Построение:

1. DE

2. ЕК

3. DК

DЕK - искомое сечение

Задача 2. Построить сечение плоскостью, проходящей через данные точки D, Е, K.

П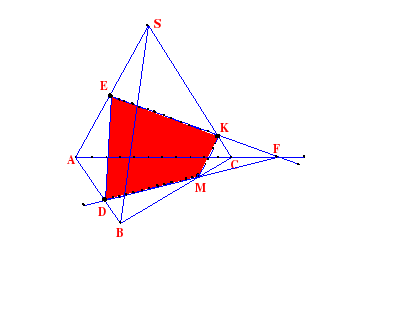остроение:

1. DE

2. ЕК

DК - нельзя

3. ЕК ∩ АС = F

4. FD

5. FD ∩ BС = M

6. KM

DЕKМ - искомое сечение

Задача 3. Построить сечение плоскостью, проходящей через точки

Т, Н, М, М Є АВ.

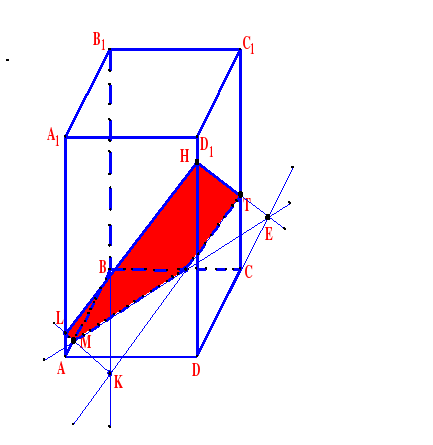
Построение:

1. НТ

2. НТ ∩ DС = E

3. ME ∩ ВС = F

4. ТF

5. ТF ∩ В1В = K

6. МK ∩ АА1= L

7. LН

НТFМL - искомое сечение

Задача 4. Построить сечение плоскостью, проходящей через данные точки Е, F, K.

П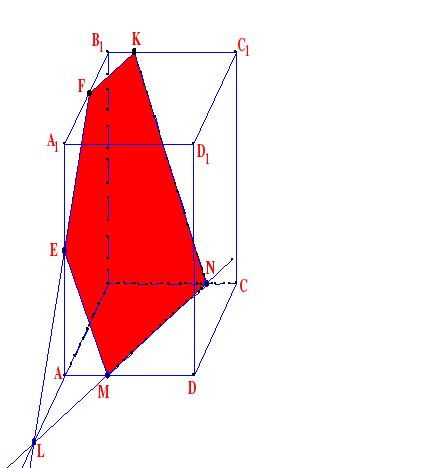остроение:

1. KF

2. FE

3. FE ∩ АB = L

4. LN ║ FK

5. LN ∩ AD = M

6. EM

7. KN

EFKNM - искомое сечение

Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р, Р Є (АВС)

П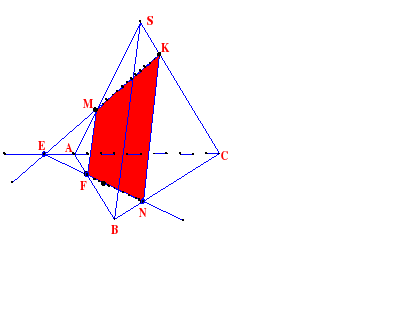остроение:

1. КМ

2. КМ ∩ СА = Е

3. EР

4. ЕР ∩ АВ = F

ЕР ∩ ВC = N

5. МF

6. NК

КМFN - искомое сечение

4. Подведение итогов урока.

5. Домашнее задание.

§ 21 (выучить теорию) (Уч. Бевз Математика 10).

Уч. Билянина с. 68

Задачи 1, 3, 5, 6, 7 (они с решением).

Постройте сечения на листе формата А4 (каждая задача на отдельном). Оформление как в классной работе:

Записать условие.

Выполнить чертеж (в цвете, оптимального размера).

Построение (кратко, каждый этап, на обратной стороне листа.)