- Учителю
- Урок по геометрии Трапеция(8 класс)
Урок по геометрии Трапеция(8 класс)
Дата:
Тема урока: Трапеция.
Цели урока:
Образовательная:
-
Ввести понятие трапеции и ее элементов, познакомить учащихся видами трапеций;
-
Рассмотреть некоторые свойства и признаки равнобедренной трапеции;
-
Научить учащихся применять полученные знания в процессе решения задач.
Развивающая:
-
Развитие у детей умения обобщать, логически мыслить, применять в своих рассуждениях аналогию, наблюдение, рационально применять свои знания;
Воспитательная:
-
Воспитание интереса к математике с помощью элементов занимательности, знакомства с историей возникновения понятия «трапеция»
Тип урока: урок изучения нового материала и первичное закрепление знаний.
Оборудование: слайды из презентации к уроку, проектор, карточка-тест.
Содержание урока:
-
Организационный момент (1 мин)
-
Актуализация опорных знаний (5-7 минут)
-
Сообщение цели и темы урока. (2-3 минуты)
-
Изучение нового материала (15 - 20 минут)
-
Ввести понятие трапеции, ее оснований и боковых сторон.
-
Ввести понятия равнобедренной трапеции, прямоугольной трапеции.
-
Изучение свойств равнобедренной трапеции.
-
Закрепление изученного материала (решение задач на готовых чертежах)
(10-12 минут) -
Самостоятельная работа в виде теста (3- 4 минуты)
-
Подведение итогов урока. Рефлексия (2 - 3 минуты)
-
Домашнее задание (1 минута)
Ход урока:
-
Организационный момент
Учитель: Здравствуйте, ребята. Сегодня на уроке мы продолжаем изучение одного из важнейших разделов геометрии - изучение четырехугольников.
Эта тема является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем.
-
Актуализация опорных знаний
Попробуем систематизировать все, что мы знаем о четырехугольниках.
Слайд 1
Р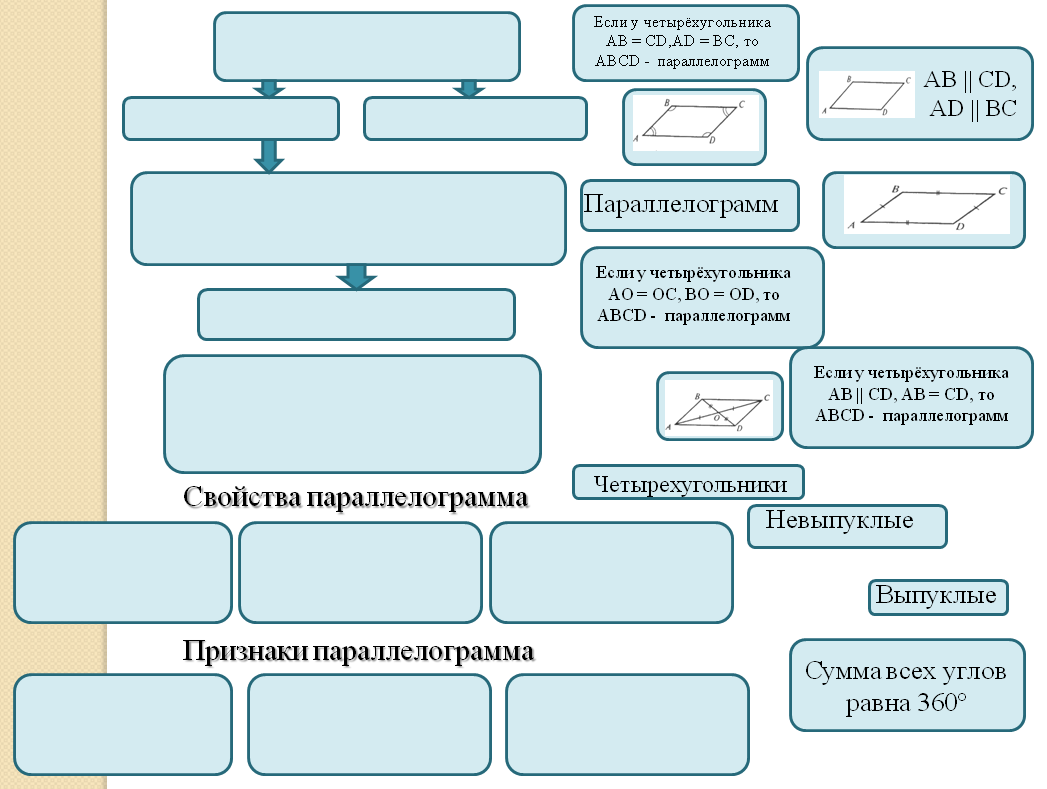 ебята, посмотрите,
пожалуйста, на слайд.
ебята, посмотрите,
пожалуйста, на слайд.
На доске представлена схема изучения геометрии 8 класса, но все понятия потеряли свои места. Ваша задача - восстановить порядок изучения материала.
Вспомогательные вопросы:
- Какие бывают четырехугольники? [Выпуклые и невыпуклые]
- Какой четырехугольник называется выпуклым? [четырехугольник - называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины]
 - Что вы можете сказать о
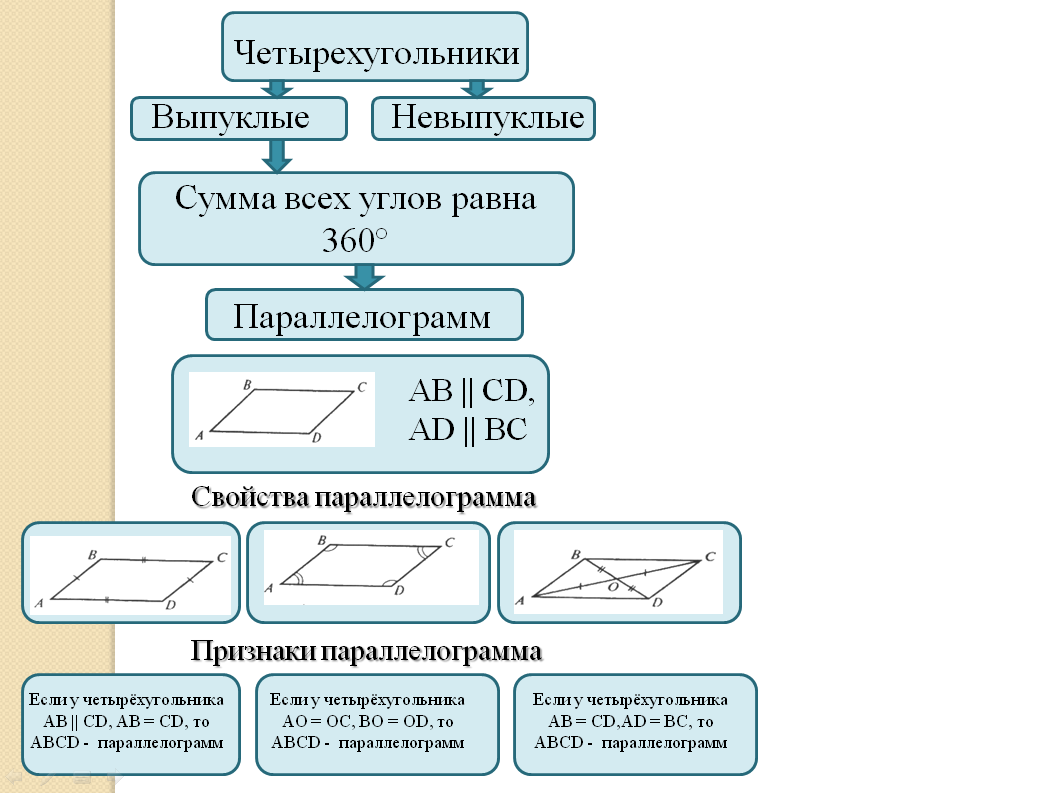
сумме углов четырехугольника? [Сумма всех углов равна 360°]
- Что вы можете сказать о
сумме углов четырехугольника? [Сумма всех углов равна 360°]
- С каким четырехугольником мы уже познакомились?[Параллелограммом]
- Дайте определение параллелограмма? [Параллелограмм - четырехугольник, у которого противоположные стороны попарно параллельны]
- Какие свойства параллелограмма мы изучили? [В параллелограмме противоположные стороны и углы равны ]; [Диагонали параллелограмма точкой пересечения делятся пополам]
- Какие признаки мы изучили?
[Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм]
[Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм]
[Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм]
- Для чего необходимо использовать признаки, а для чего применять свойства?
[Свойство - это характерная особенность, присущая только этой геометрической фигуре. Признак - это характерная особенность, по которой ищут в многообразии других фигур именно эту].
Молодцы! Вы хорошо справились с заданием!
-
Сообщение цели и темы урока.
С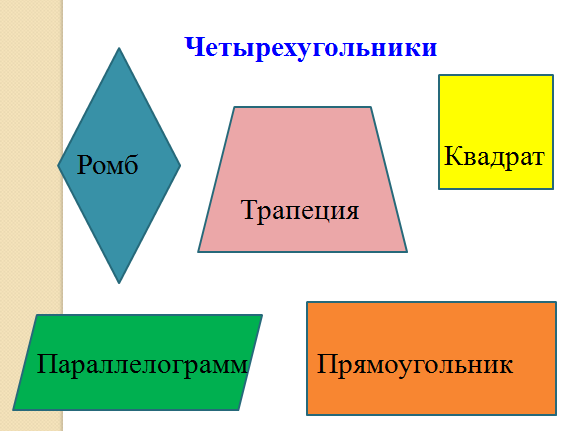 лайд 2
лайд 2
На доске вы видите разные виды четырехугольников.
- Как вы думаете, у всех ли четырехугольников противоположные стороны параллельны? (Выслушиваются ответы учеников).
-А может ли существовать четырехугольник, у которого только одна пара сторон параллельна?
- А как такие четырехугольники называются?
Итак, какова тема нашего урока? [Трапеция]
- Запишем тему урока: Трапеция.
Мы уже изучили параллелограмм, вспомнили с вами структуру изучения темы? По аналогии с параллелограммом, скажите, что мы узнаем о трапеции?
[ Сегодня на уроке мы
познакомиться с еще одним видом четырехугольников - трапецией,
узнаем о её видах, свойствах и признаках; научимся применять эти
свойства и признаки при решении задач.]
Сегодня на уроке мы
познакомиться с еще одним видом четырехугольников - трапецией,
узнаем о её видах, свойствах и признаках; научимся применять эти
свойства и признаки при решении задач.]
-
Изучение нового материала
- Правильно, а сейчас послушаем рассказ подготовленный Самуйленковым Степаном и узнаем, почему этот четырехугольник - носит такое название?
-
Понятие трапеции формировалось в течение длительного периода времени. «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посейдона. Сначала трапецией называли любой четырехугольник, не являющийся параллелограммом . Именно в таком смысле термин «трапеция» использовал Евклид в своих «Началах». Лишь в XVIII в. это слово приобретает современный смысл.
-
«Трапеция» - слово греческого происхождения, означавшее в древности «столик» (по гречески «трапедзион» означает столик, обеденный стол).
- Спасибо, Степа! [Сообщение оценки]
-
Ввести понятие трапеции, ее оснований и боковых сторон.
В тетрадях и на доске рисунок и записи
Слайд 3
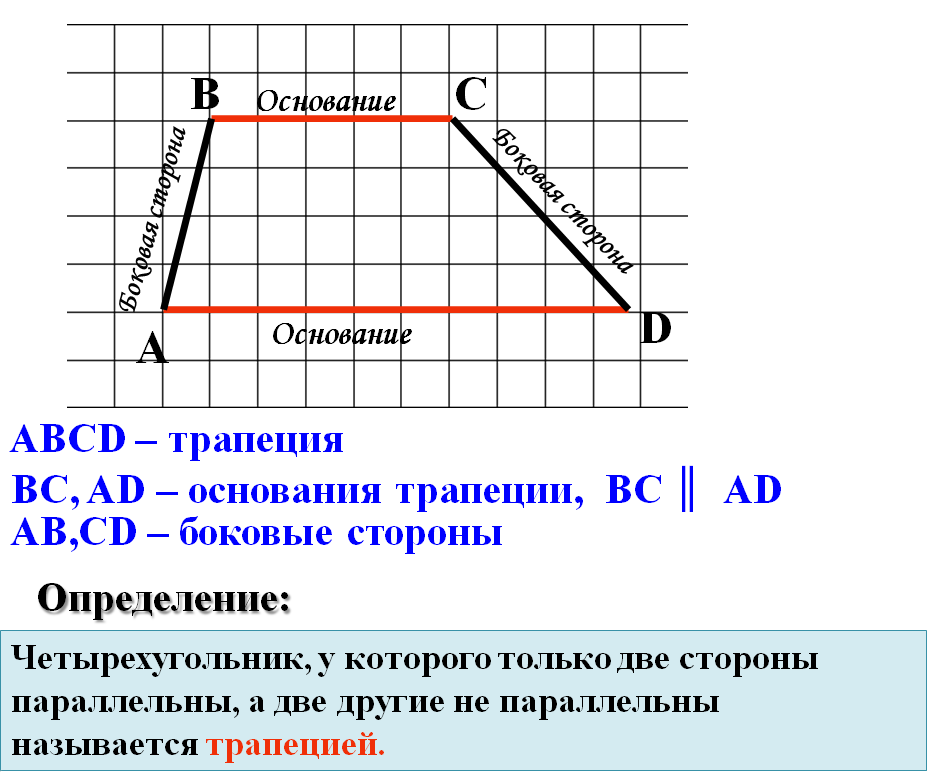 - Ребята, посмотрите на
трапецию и дайте определение трапеции самостоятельно.
[Выслушиваются ответы учеников].
- Ребята, посмотрите на
трапецию и дайте определение трапеции самостоятельно.
[Выслушиваются ответы учеников].
- Проверьте себя, прочитайте определение в учебнике. ( страница 103)
- Как называются параллельные стороны? [Основания]
Как называются две другие стороны? [боковые стороны]
- Параллельные стороны не могут быть равными? [ Нет, так как в противном случае мы имели бы параллелограмм]
- Правильно, поэтому одну из них мы назовем большим, вторую - малым основаниями трапеции.
2. Ввести понятия равнобедренной трапеции, прямоугольной трапеции. В тетрадях и на доске рисунки и записи. Слайд 4.
 - Какие стороны у трапеции
могут быть равными? [Боковые]
- Какие стороны у трапеции
могут быть равными? [Боковые]
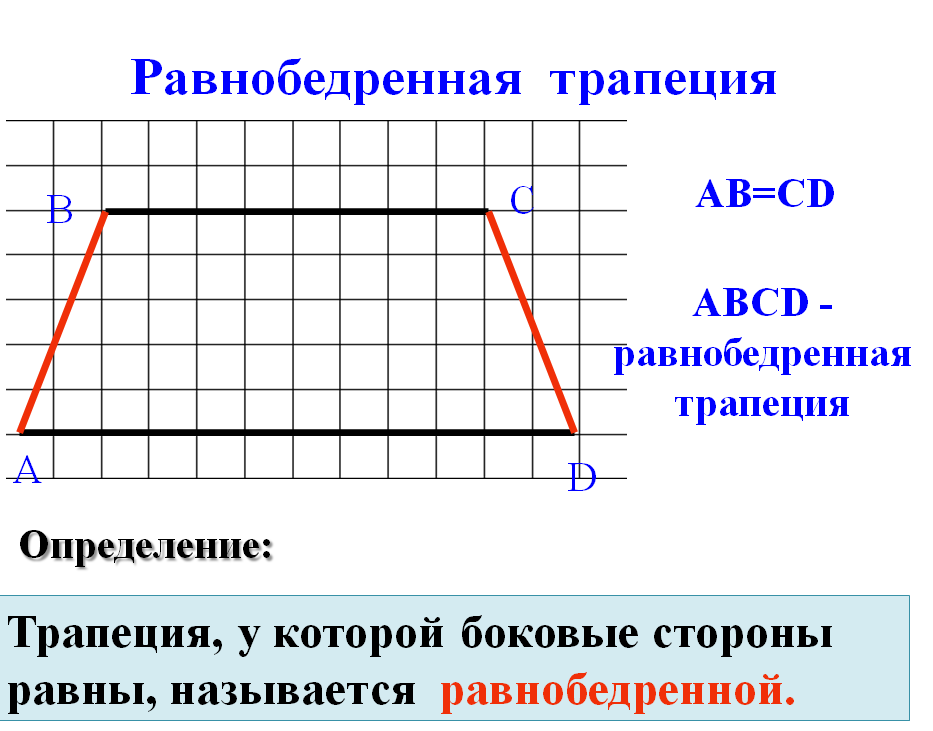
В зависимости от длин боковых сторон и их расположения трапеции
могут быть различных видов. Рассмотрим виды трапеции.
В 7 классе мы изучали треугольник, у которого две равные стороны. Как он называется? [равнобедренный]
Как называется трапеция, которой боковые стороны равны? [равнобедренная]
Слайд 5.
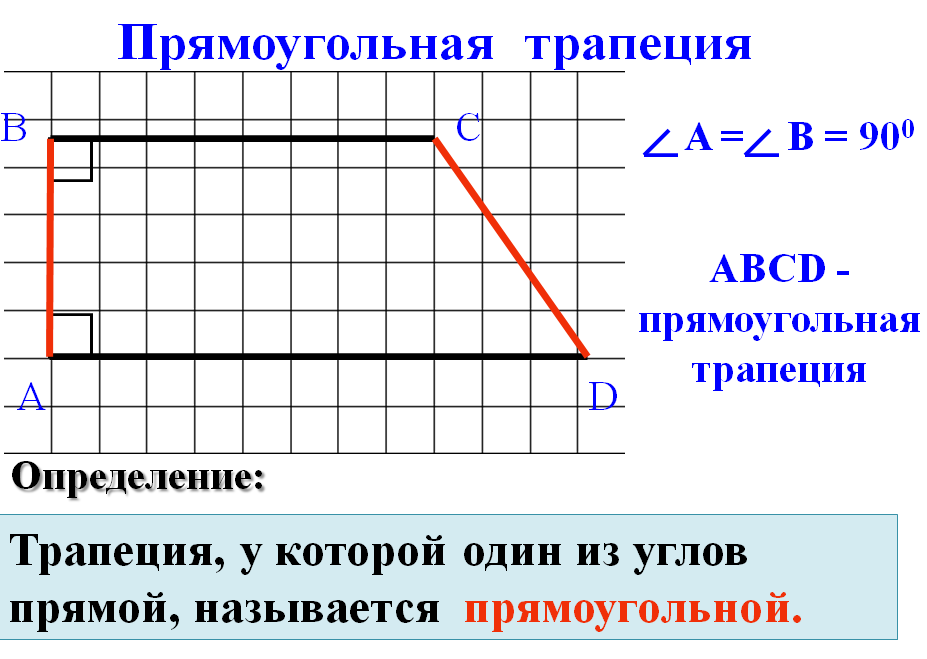
- Следующий вид трапеции - прямоугольная трапеция.
Дайте определение прямоугольной трапеции самостоятельно.
Подведем итог: Трапеция - это ...[ответ учащихся]
Трапеции бывают ...[ответ учащихся]
Какая трапеция называется равнобедренной? прямоугольной ...[ответ учащихся]
-
Изучение свойств равнобедренной трапеции.
- Равнобедренная трапеция обладает основными свойствами. Эти свойства мы выведем, решая задачу.
Рассмотрим задачу с учебника №388(а)
№ 388 (а).
В равнобедренной трапеции углы при основании равны.

1. Дополнительные построения: СЕ||АВ.
2. ABСЕ - параллелограмм (СЕ||АВ, АЕ||ВС) => АВ=СЕ.
3. АВ=СЕ=СD=> ![]() СЕD
равнобедренный =>
СЕD
равнобедренный => ![]() 1=
1=![]() 2.
2.
4. Так как АВ||СЕ, то ![]() 3=
3=![]() 2 - как соответственные =>
2 - как соответственные =>
![]() 3=
3=![]() 1.
1.
5. ![]() В=180º-
В=180º-![]() 3=180º-
3=180º-![]() 1=
1=![]() С.
С.
Ч.т.д.
В ходе решения задачи, учитель задает наводящие вопросы:
-
При решении задач, мы используем свойства и признаки уже изученных фигур. Для этого необходимы дополнительные построения. Подумайте, на какие фигуры можно разбить трапецию? Что для этого надо сделать? [Построить отрезок СЕ, такой что СЕ||АВ.]
-
Что вы можете сказать о четырехугольнике ABСЕ? [ABСЕ - параллелограмм (СЕ||АВ, АЕ||ВС) => АВ=СЕ.]
-
Рассмотрим другую фигуру - треугольник СЕD. Какой это треугольник? [Равнобедренный, т.к. АВ=СЕ=СD].
Какими свойствами обладает равнобедренный треугольник? [В равнобедренном треугольнике углы при основании равны, значит 1=
1= 2.]
2.]
-
Скажите, можно ли утверждать что
 3 =
3 =
 2? Как называются эти
углы?
2? Как называются эти
углы?
Итак, если 1=
1= 2 , а
2 , а  2=
2= 3 значит
3 значит  3=
3= 1
1
-
Мы доказали равенство углов при большем основании. Как доказать, что
 В=
В= С?
С?
Что вы можете сказать о А и
А и
 В? [односторонние]. Что
мы знаем про односторонние углы? [сумма односторонних углов
равна 180]
В? [односторонние]. Что
мы знаем про односторонние углы? [сумма односторонних углов
равна 180]
Слайд 6. № 388 (б) прочитать задачу.
-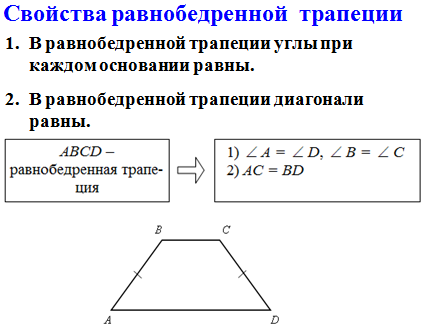 Доказательство этого
свойства, вы проведете дома самостоятельно.
Доказательство этого
свойства, вы проведете дома самостоятельно.
В тетрадях и на доске рисунок и записи:
Слайд 7.
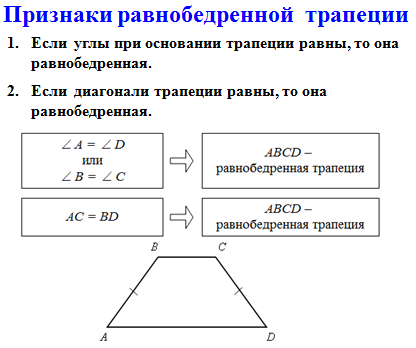 - Сформулируйте утверждения,
обратные свойствам равнобедренной трапеции. Как называются эти
обратные свойства? [признаки равнобедренной трапеции]
- Сформулируйте утверждения,
обратные свойствам равнобедренной трапеции. Как называются эти
обратные свойства? [признаки равнобедренной трапеции]
-
Закрепление изученного материала (решение задач на готовых чертежах)
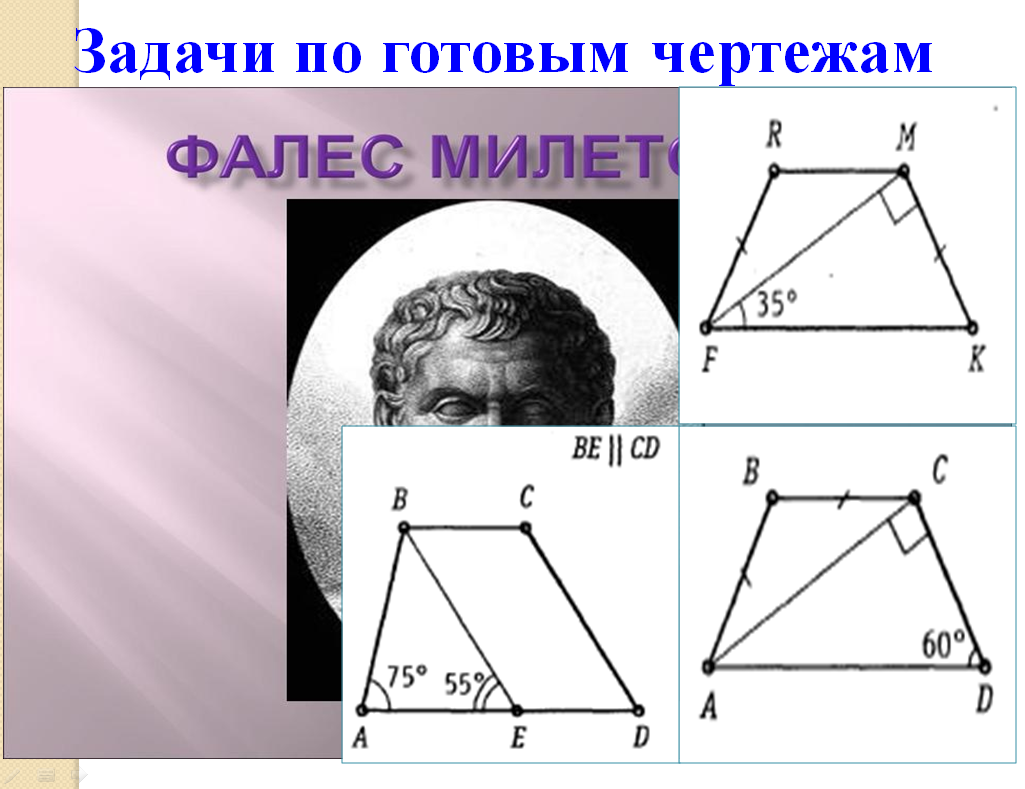
С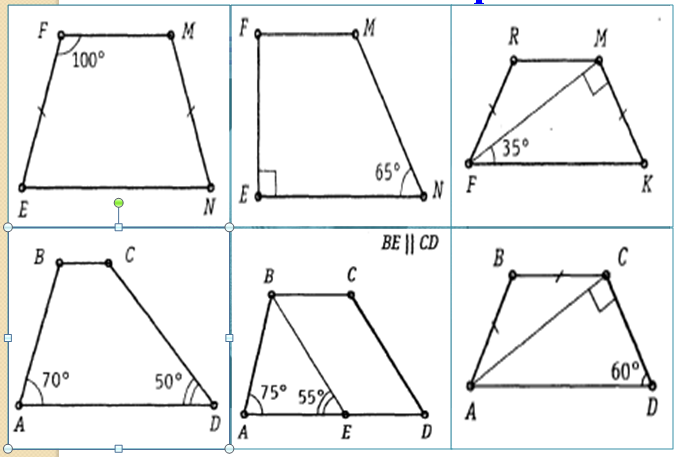 ейчас я предлагаю вам узнать
имя ученого, спрятанного за сеткой задач. При правильном ответе
сектор открывается и появляется часть изображения.
ейчас я предлагаю вам узнать
имя ученого, спрятанного за сеткой задач. При правильном ответе
сектор открывается и появляется часть изображения.
Много интересного рассказывают про этого учёного. Вот, например, один случай. Учёный, наблюдая звёзды, упал в колодец, а стоявшая рядом женщина посмеялась над ним, сказав: «Хочет знать, что делается на небе, а что у него под ногами, не видит»
Этот учёный сформулировал следующие теоремы: а) Вертикальные углы равны; б) В равнобедренном треугольнике углы при основании равны; в)Если на одной стороне угла отложить равные отрезки, и провести через них параллельные прямые, то и на другой стороне угла отложатся равные отрезки.
Слайд 8
 Ответы:
Ответы:
( слева - направо, 1 ряд - 2 ряд )
1) Е = N = 80;M = 100.
2) F = 90;M=115
3) К =F = 55;M=R= 125;
4) B = 110;M=130
5) D = 55;C=125;F = 105
6) C = 120;A=60;B = 120
При отсутствии времени количество задач сократить, решив их на следущем уроке.
-
Самостоятельная работа в виде теста
Слайд 9.ТЕСТ
Определить вид четырехугольника если он имеет:
Трапеция
Паралле-лограмм
Равнобед-ренная
Прямо-угольная
Разносто-ронняя
два прямых угла и все стороны разные
+
два разных острых угла и все разные стороны
+
два одинаковых тупых угла и две одинаковые боковые стороны
+
противоположные стороны равны и углы равны
+
-
Подведение итогов урока. Рефлексия.
Ребята, что нового вы узнали на уроке?
Что было особенно интересно?
На что еще необходимо обратить внимание? -
Домашнее задание
П. 44, записи в тетрадях, № 388(б), № 390.
Придумать и решить задачу на использование свойства или признака трапеции.