- Учителю
- Открытый урок алгебры по теме Квадратные уравнения
Открытый урок алгебры по теме Квадратные уравнения
Тема: Квадратные уравнения.
Эпиграф к уроку: "Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным".
Паскаль
Цели:
-
Показать уровень усвоения программного материала по теме «Квадратные уравнения», навыки решения квадратных уравнений с помощью применения формул корней квадратных уравнений, изучить новый способ решения квадратных уравнений.
-
Развитие вычислительных навыков: навыков решения квадратных уравнений с помощью формул, навыки нахождения дискриминанта квадратного уравнения, развитие логического мышления,
-
Способствовать рациональной организации труда, внимательность, активное участие в учебно-познавательном процессе, самостоятельность, самокритичность.
Оборудование к уроку: тест "Квадратные уравнения", интерактивная доска, таблицы, карточки.
План урока
-
Организационный момент "Настроимся на урок!"
-
Проверка домашнего задания
-
Тест "Квадратные уравнения".
-
Работа в парах: математика и биология.
-
Немного истории.
-
Продвинутые способы решения квадратных уравнений
-
Викторина "Дальше, дальше..."
-
Итог.
Ход урока
1. Организационный момент "Настроимся на урок!"
Здравствуйте, ребята и гости нашего урока! Математику не зря называют "царицей наук", ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Эпиграфом к уроку я взяла слова великого математика Паскаля "Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным". В течение урока мы еще вернемся к этим словам.
Мы с вами начали изучать новый большой раздел «Квадратные уравнения». И вы уже достаточно знаете и умеете по этой теме, и сегодня наша с вами задача обобщить все те знания и умения, которые у вас есть. Но знания надо не только иметь, их надо еще и уметь показать, что вы и сделаете на сегодняшнем уроке, а я вам в этом помогу.
Каждый из вас имеет возможность получить оценку за урок по результатам работы на различных его этапах. Для этого у вас на партах лежат карты результативности, в которые вы будете фиксировать свой успех в баллах. Но, есть один не- обсуждаемый закон: для ответа на поставленный вопрос вы поднимаете руку и ни в коем случае не перебиваете друг друга. Желаю всем удачи.
Карта результативности.
Вопросы
Теории
1 балл за верный ответ
Тест
1 балл за верный ответ
Черный ящик
1 балл
Матем. Лото
С первого раза-3 балла; со второго-2б., с третьего-1 балл.
Сам.
Работа
1 балл за верный ответ
Викторина
1 балл за верный ответ
ИТОГО
Кол-во
баллов
2. Проверка домашнего задания
Начнем урок с проверки теоретического материала, который понадобится нам на протяжении всего урока.
-
Какой вид имеет квадратное уравнение? Что такое a, b, c, x?
-
Какие именно квадратные уравнения бывают? (полные и неполные, приведеные).
-
Какие уравнения называются приведенными?
-
Сколько решений имеет полное квадратное уравнение? От чего это зависит?
-
Назовите формулу дискриминанта- напишите на доске.
-
Напишите формулу корней квадратного уравнения.
-
Расскажите теорему Виета. Запишите ее на доске.
3. Тест "Квадратные уравнения".
Замечательно, теорию мы повторили, но важно не только знать ее, важно уметь правильно ее применять. Поэтому сейчас я хотела бы проверить, как вы научились справляться непосредственно с решением квадратных уравнений. У вас на столах лежат карточки с заданиями, в течении 5 минут вам необходимо вписать в них пропущенные слова, формулы, найденные корни уравнений. Приступаем к работе.
Ученики получают карточки с заданиями. Заполняют пропущенные слова в карточках.
I ВАРИАНТ
1. Уравнение вида ![]() , где a, b,
c - заданные числа, a
, где a, b,
c - заданные числа, a![]() 0, x -
переменная, называется...
0, x -
переменная, называется...
2. Полное квадратное уравнение не имеет корней, если D ...
3. Уравнение вида ![]() называется...
называется...
4. Квадратное уравнение имеет два корня,
если![]() ...
...
5. Дано уравнение ![]() . D =...
. D =...
6. Найдите корни уравнения: 3x² - 5x +2 = 0
II ВАРИАНТ
1. Если ![]() квадратное
уравнение, то a... коэффициент, с...
квадратное
уравнение, то a... коэффициент, с...
2. Уравнение x² = a, где a < 0, не имеет...
3. Полное квадратное уравнение имеет
единственный корень, если ![]() ...
...
4. Уравнение вида ax² + c = 0, где
a ![]() 0, c
0, c
![]() 0, называют
... квадратным уравнением.
0, называют
... квадратным уравнением.
5. Дано уравнение x²- 6x + 8 = 0. D =...
6. Найдите корни уравнения: 2x² - 5x +3 = 0
Проводится взаимопроверка. Ответы показываем через интерактивную доску.
Результат заносят в "Карту результативности".
Нет ошибок - 6 б.
1 - 1 ош. - 5б.
3 - 2 ош. - 4б.
5 - 3 ош. - 3б.
Более 4 ош. - 0 б.
4. Работа
Вернемся к эпиграфу нашего урока. Попытаемся сделать математику хотя бы сегодня на уроке немного более занимательной.
Вам необходимо угадать, что же находится в черном ящике.
Математика и биология
Учитель: Даю три определения этому предмету:
1. Непроизводная основа слова.
2. Число, которое после постановки его в уравнение обращает уравнение в тождество.
3. Один из основных органов растений.
/Корень/
Учитель: Видите, ребята, все в этом мире взаимосвязано: математика, русский язык и литература, биология. Слово корень встречается вам на разных уроках. А теперь вы должны определить, какого растения это корень, сыграв со мной в «математическое лото».
У вас на партах лежит листок с уравнениями, которые необходимо решить в парах, по истечении 10 минут на экране появятся карточки лото с различными вариантами ответов, вам нужно будет найти правильный карточку.
1. x²- 8x + 15 = 0 4. x² - 11x + 18 = 0
2. x² - 5x - 6 = 0 5. x² - 4x + 4 = 0
3. 3x² + 4x + 20 = 0 6. 5x²- 3x - 2 = 0
Если ученики получают правильный ответ, то получат изображение розы, иначе - слайд с текстом «Проверьте решение».
Учитель: Что это за растение?
Ответ: Роза.
Учитель: Значит, в черном ящике лежал корень розы, о которой в народе говорят: "Цветы ангельские, а когти дьявольские".
-
Немного истории.
Уравнения как таковы в целом волновали умы человечества еще с давних времен. Великий математик Лейбница, считал, что тот "кто хочет ограничиться настоящим без знания прошлого, никогда его не поймет", т.е невозможно понять настоящее не зная его прошлого. А вы знаете, когда появились первые квадратные уравнения?
Задачи на квадратные уравнения встречаются уже в 499 г. в работе индийского математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму. К таким задачам мы еще вернемся сегодня.
-
Продвинутые способы решения квадратных уравнений
Квадратные уравнения - считаются фундаментом, на котором покоится величественное здание алгебры. Они очень важны не только для математики, но и для других наук. По этому поводу у английского поэта средних веков Чосера есть прекрасные строки:
Посредством уравнений, теорем
Я уйму всяких разрешил проблем.
В школьном курсе математики мы изучаем разные способы решения квадратных уравнений. Какие это способы? (5 сп.) Но имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Всего в математической науке есть десять способов решения квадратных уравнений.
Способы решения квадратных уравнений, изучаемые в школе:
-
Разложение левой части на множители
-
Метод выделения полного квадрата
-
С применением формул корней квадратного уравнения
-
С применением теоремы Виета
-
Графический способ
Продвинутые способы решения квадратных уравнений:
-
Способ переброски
-
По свойству коэффициентов
-
С помощью циркуля и линейки
-
С помощью номограммы
-
Геометрический
А как вы думаете зачем они все нам нужны? Не проще было бы выучить один способ и решать все по шаблону? Я отвечу словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».
Сегодня на уроке мы познакомимся с одним из способв решения квадратных уравнений, который не изучается в школе. Но он очень интересный и вовсе не сложный.
Решение квадратных уравнений по свойству коэффициентов.
С Формулами, выражающими зависимость корней уравнения от его коэффициентов,мы уже встречались при решении уравнений по теореме Виета. А что Вы знаете об этом ученом? На вопросы отвечает наиболее подготовленный ученик, демонстрируя презентацию «Франсуа Виет».
французский математик, основоположник символической алгебры</<font size="4">. По образованию и основной профессии - юрист. В 1591 вывел формулы, выражающие зависимость корней от его коэффициентов, он же и ввел в математике термин коэффициент, т.е Сопутсвующий.
Пусть дано квадратное уравнение
ах2 + bх + с = 0, где а ≠0.
Свойство 1.
Если а + b + с = 0 (т е. сумма коэффициентов уравнения равна нулю), то х1 = 1, х2 = с/а
Свойство 2.
Если b = а + с, то
х1 = - 1, х2 = - с/а
Давайте переведем эти свойства с математического языка.
Пример:
![]()
Хорошо. Вместе мы поработали. Теперь посмотрим, как вы умеете работать самостоятельно
Решите самостоятельно:
1 вариант: ![]() 2 вариант:
2 вариант:
![]()
За правильно решенное уравнение вы получаете 1 балл.
7. Викторина. "Дальше, дальше..."
Для того чтобы все подъитожить, предлагаю вам небольшую устную викторину. Но вопросы будут не только по теме урока, проверяем ваше внимание и умение переключаться. За каждый правильный ответ в колонку "Викторина" вы ставите 1 балл.
В течение одной минуты ребята отвечают на вопросы, приведенные ниже:
1. Уравнение второй степени.
2. Сколько корней имеет квадратное уравнение, если D больше 0?
3. Равенство с переменной?
4. Сколько раз в году встает солнце?
5. От чего зависит количество корней квадратного уравнения?
6. Как называется квадратное уравнение, у которого первый коэффициент - 1?
7. Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?
8. Что значит решить уравнение?
9. Когда начался двадцать первый век?
10. Есть у любого слова, у растения и может быть у уравнения?
7. Итог урока.
Учитель:
Итак, мы проделали большую работу. Что нового мы узнали на уроке?
Также мы не только узнали новое но и повторили старое,повторили всю теорию, касающуюся полных и неполных квадратных уравнений. Решали различные их виды как вместе, так и вы сами. Вы старательно зарабатывали баллы, настало время подвести итог.
Подсчитайте сумму баллов, заработанных в течение урока.
Критерии оценивания:
14 и более баллов - "5".
11-13- баллов - "4".
8-10 баллов - "3".
Итог урока: выставление оценок
И закончить сегодняшний урок хотелось словами басни:
Мартышка - апельсинов продавщица,
Приехав как-то раз к себе на дачу,
Нашла там интересную задачу.
Но сосчитать не в силах стройный ряд,
Разбрасывать вдруг стала все подряд
И молвила: «Что толку в той задаче,
Коль из нее не слепишь новой дачи».
Я верю все же, что мартышки мненье -
Не истинно для тех, кто знает толк в ученье.
И я прошу девчонки и мальчишки,
Решить « старинную задачу дома про мартышек».
Задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?
Оценивание учащихся. Сообщение домашнего задание.
Карта результативности:
Вопросы
Теории
1 балл за верный ответ
Тест
1 балл за верный ответ
Черный ящик
1 балл
Матем. Лото
С первого раза-3 балла; со второго-2б., с третьего-1 балл.
Сам.
Работа
1 балл за верный ответ
Викторина
1 балл за верный ответ
ИТОГО
Кол-во
баллов
Карта результативности:
Вопросы
Теории
1 балл за верный ответ
Тест
1 балл за верный ответ
Черный ящик
1 балл
Матем. Лото
С первого раза-3 балла; со второго-2б., с третьего-1 балл.
Сам.
Работа
1 балл за верный ответ
Викторина
1 балл за верный ответ
ИТОГО
Кол-во
баллов
Карта результативности:
Вопросы
Теории
1 балл за верный ответ
Тест
1 балл за верный ответ
Черный ящик
1 балл
Матем. Лото
С первого раза-3 балла; со второго-2б., с третьего-1 балл.
Сам.
Работа
1 балл за верный ответ
Викторина
1 балл за верный ответ
ИТОГО
Кол-во
баллов
Карта результативности:
Вопросы
Теории
1 балл за верный ответ
Тест
1 балл за верный ответ
Черный ящик
1 балл
Матем. Лото
С первого раза-3 балла; со второго-2б., с третьего-1 балл.
Сам.
Работа
1 балл за верный ответ
Викторина
1 балл за верный ответ
ИТОГО
Кол-во
баллов
Карточки с заданиями, где нужно заполнить пропущенные слова.
Ф.И.___________________
I ВАРИАНТ
-
Уравнение вида
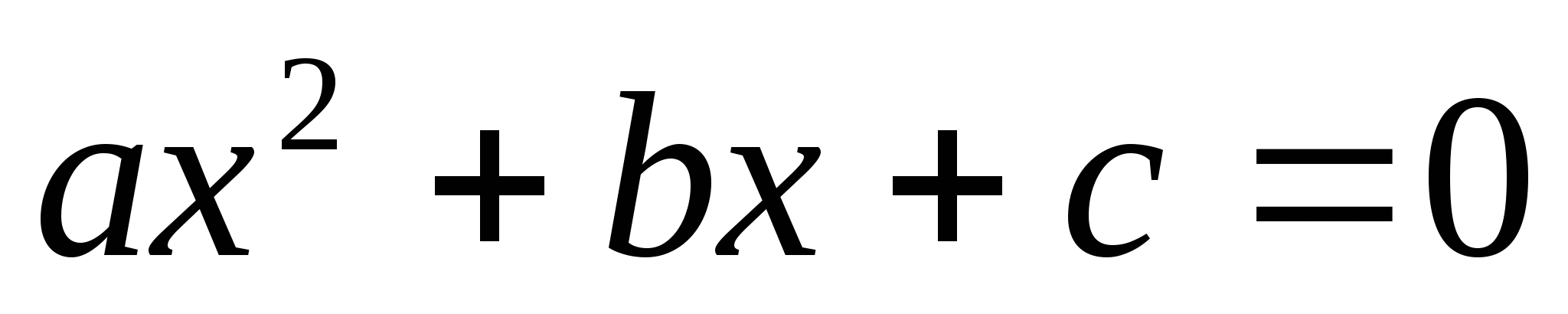 , где a,
b, c - заданные числа, a
, где a,
b, c - заданные числа, a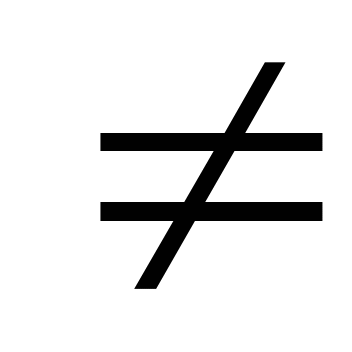 0, x -
переменная, называется...
0, x -
переменная, называется...
-
Полное квадратное уравнение не имеет корней, если D ...
-
Уравнение вида
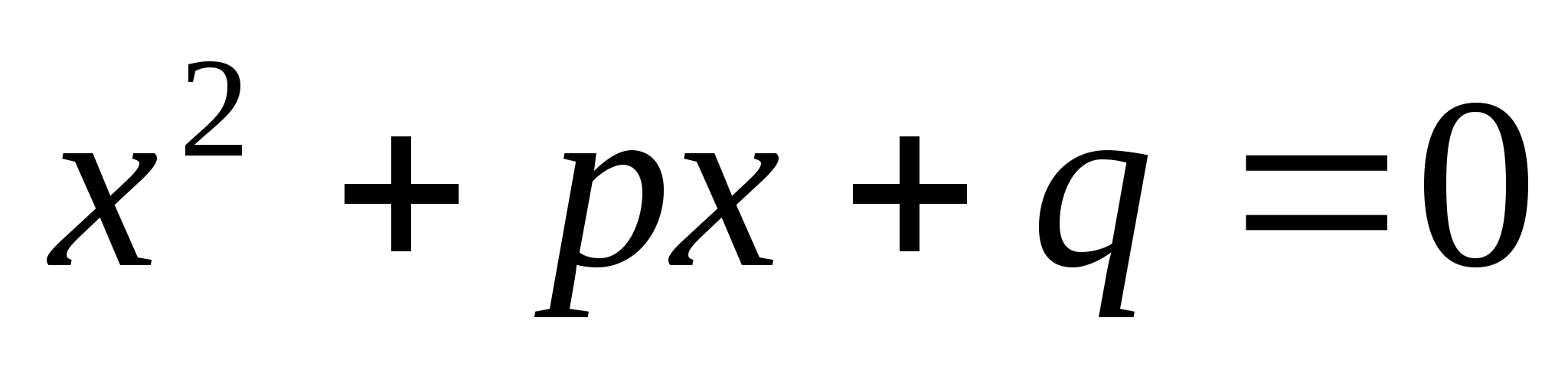 называется
...... квадратным уравнением
называется
...... квадратным уравнением
4. Квадратное уравнение имеет два корня,
если![]() ...
...
5. Дано уравнение ![]() . D =...
. D =...
6. Найдите корни уравнения: 3x² - 5x +2 = 0
Карточки с заданиями, где нужно заполнить пропущенные слова. Ф.И.___________________
II ВАРИАНТ
-
Если
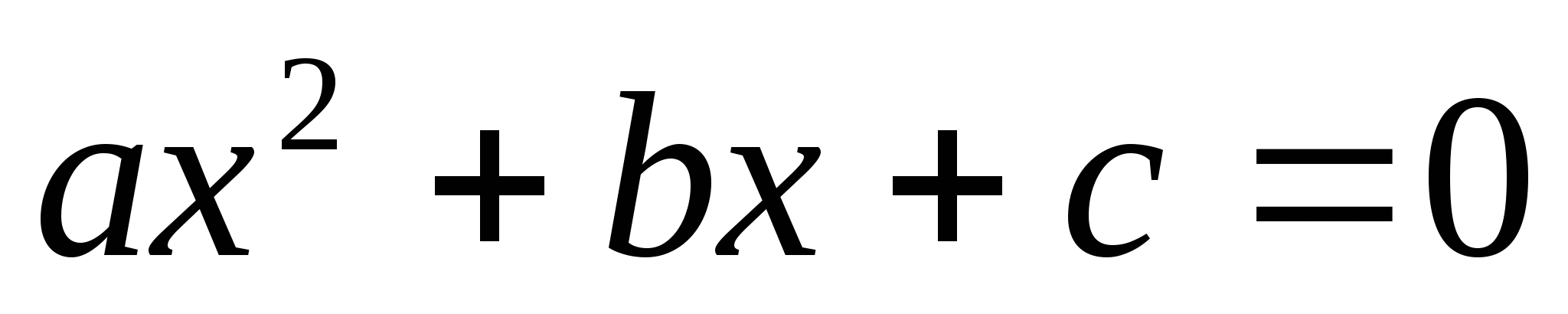 квадратное уравнение, то a... коэффициент, с...
квадратное уравнение, то a... коэффициент, с...
-
Уравнение x² = a, где a < 0, не имеет...
-
Полное квадратное уравнение имеет единственный корень, если
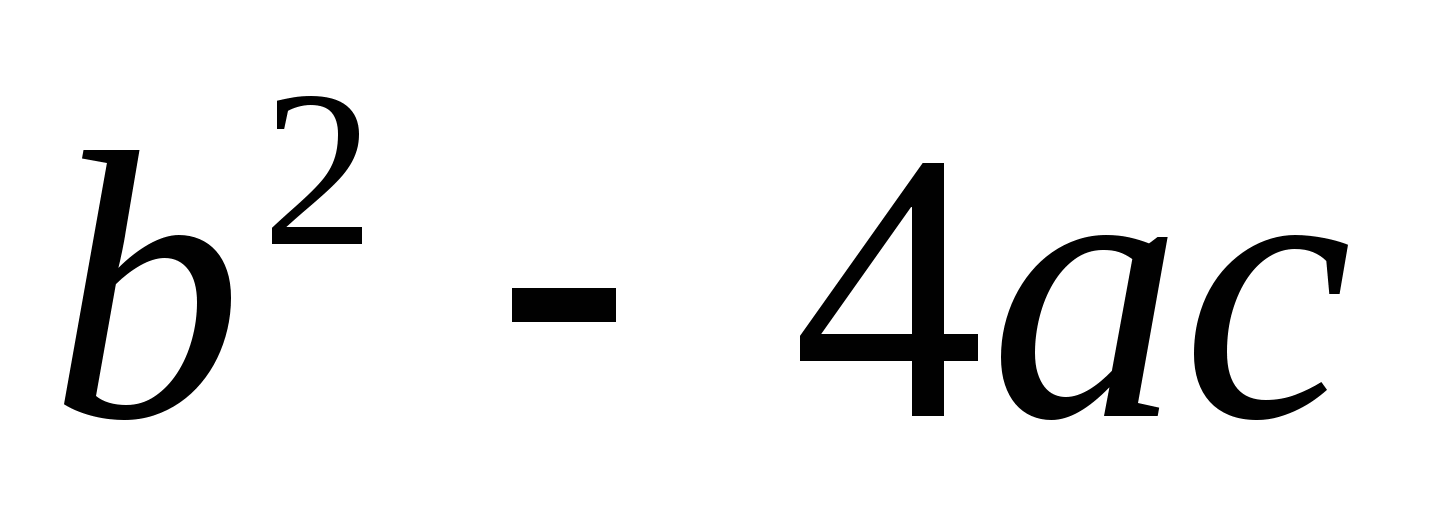 ...
...
-
Уравнение вида ax² + c = 0, где a
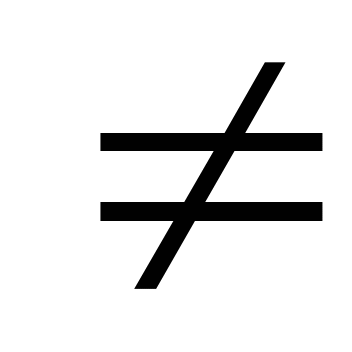 0, c
0, c
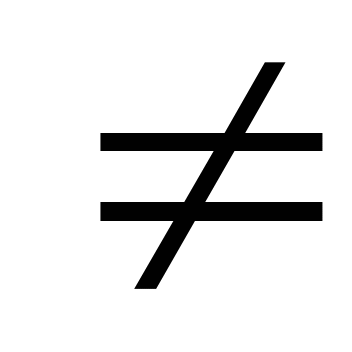 0,
называют ….. квадратным уравнением.
0,
называют ….. квадратным уравнением.
-
Дано уравнение x²- 6x + 8 = 0. D =...
-
Найдите корни уравнения: 2x² - 5x +3 = 0
Карточки с заданиями, где нужно заполнить пропущенные слова. Ф.И.___________________
I ВАРИАНТ
-
Уравнение вида
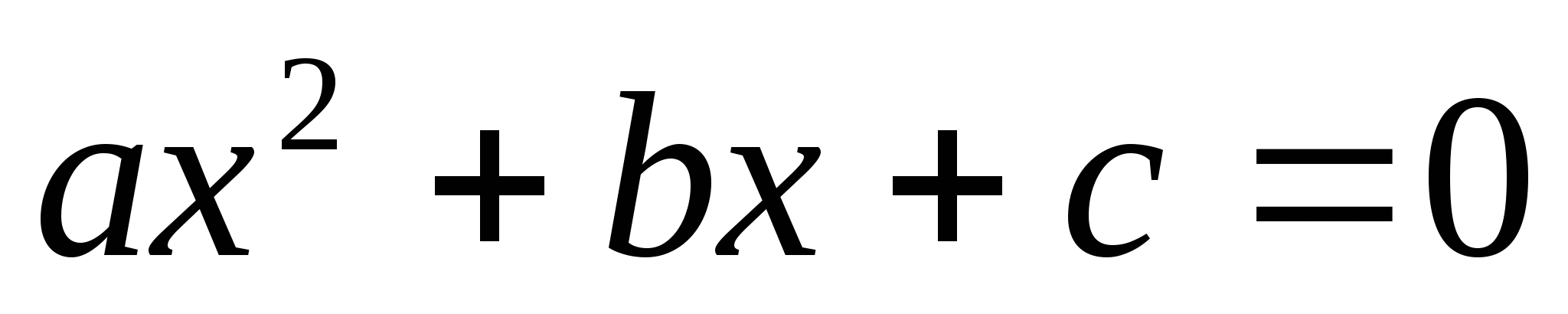 , где a,
b, c - заданные числа, a
, где a,
b, c - заданные числа, a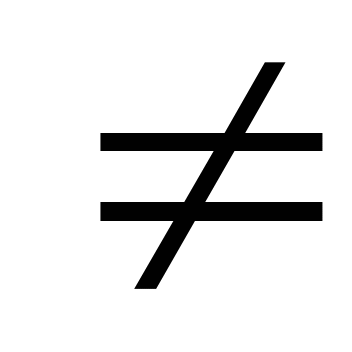 0, x -
переменная, называется...
0, x -
переменная, называется...
-
Полное квадратное уравнение не имеет корней, если D ...
-
Уравнение вида
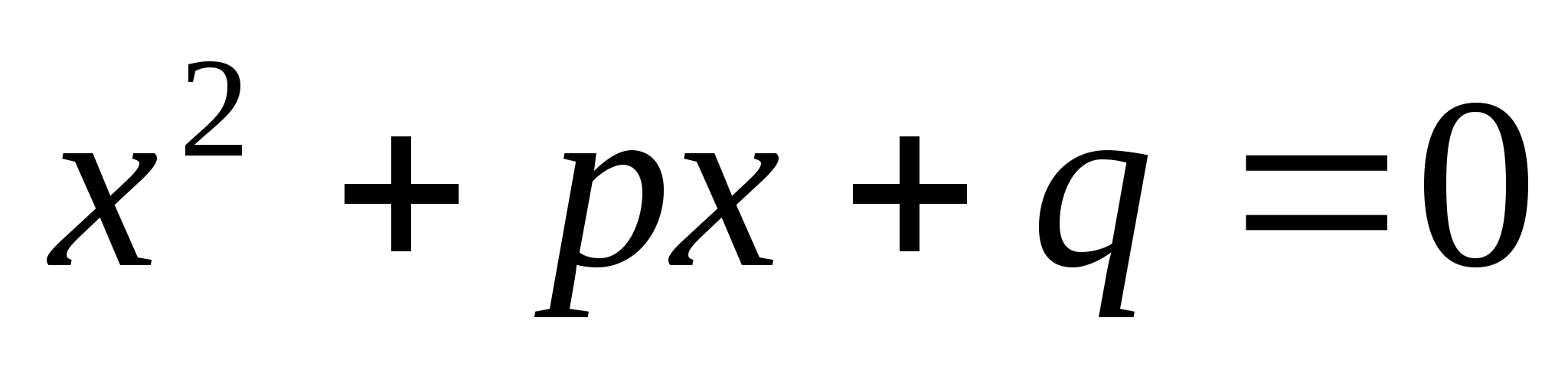 называется ...... квадратным уравнением
называется ...... квадратным уравнением
4. Квадратное уравнение имеет два корня,
если![]() ...
...
5. Дано уравнение ![]() . D =...
. D =...
6. Найдите корни уравнения: 3x² - 5x +2 = 0
Карточки с заданиями, где нужно заполнить пропущенные слова. Ф.И.___________________
II ВАРИАНТ
-
Если
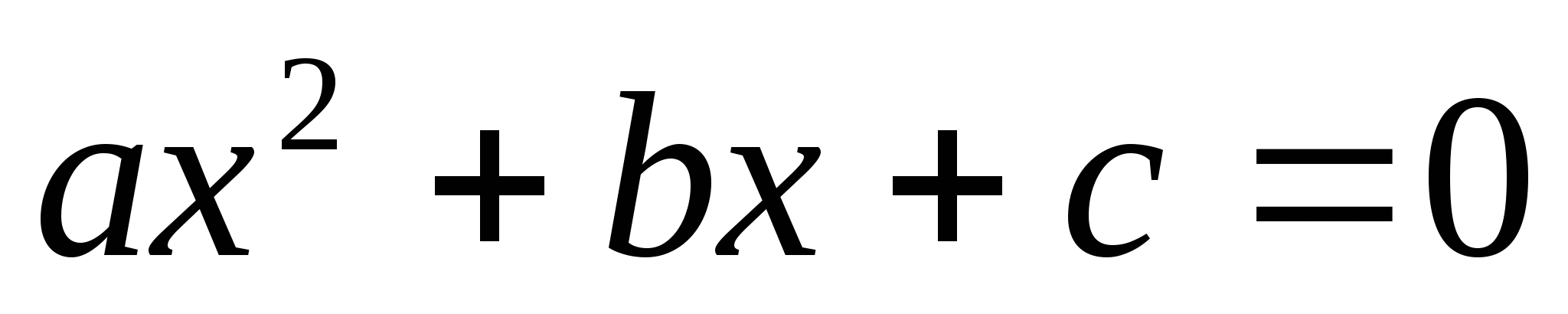 квадратное уравнение, то a... коэффициент, с...
квадратное уравнение, то a... коэффициент, с...
-
Уравнение x² = a, где a < 0, не имеет...
-
Полное квадратное уравнение имеет единственный корень, если
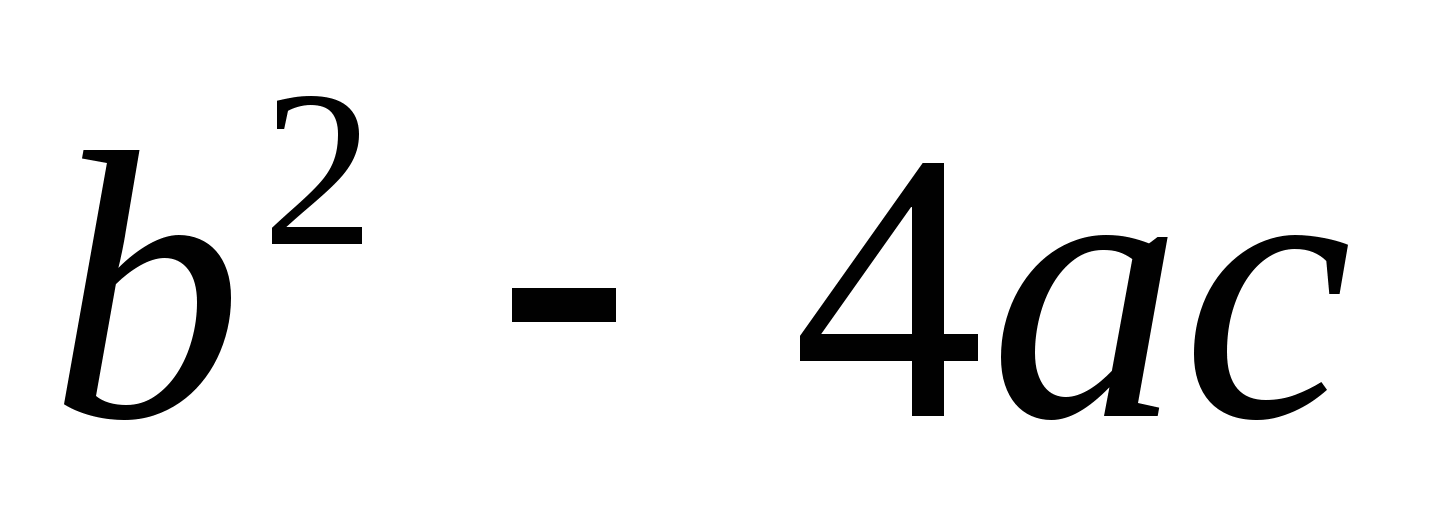 ...
...
-
Уравнение вида ax² + c = 0, где a
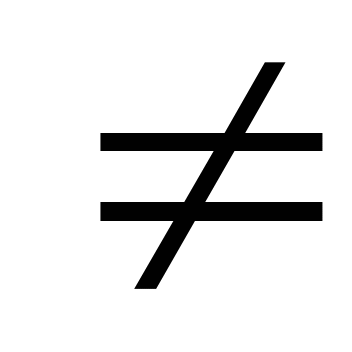 0, c
0, c
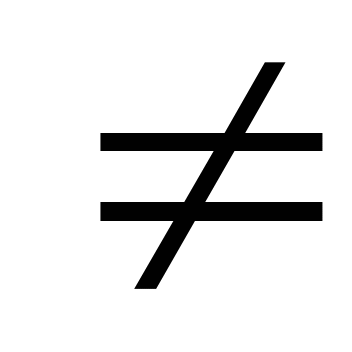 0,
называют ..... квадратным уравнением.
0,
называют ..... квадратным уравнением.
-
Дано уравнение x²- 6x + 8 = 0. D =...
-
Найдите корни уравнения: 2x² - 5x +3 = 0
Карточки с заданиями, где нужно заполнить пропущенные слова. Ф.И.___________________
I ВАРИАНТ
-
Уравнение вида
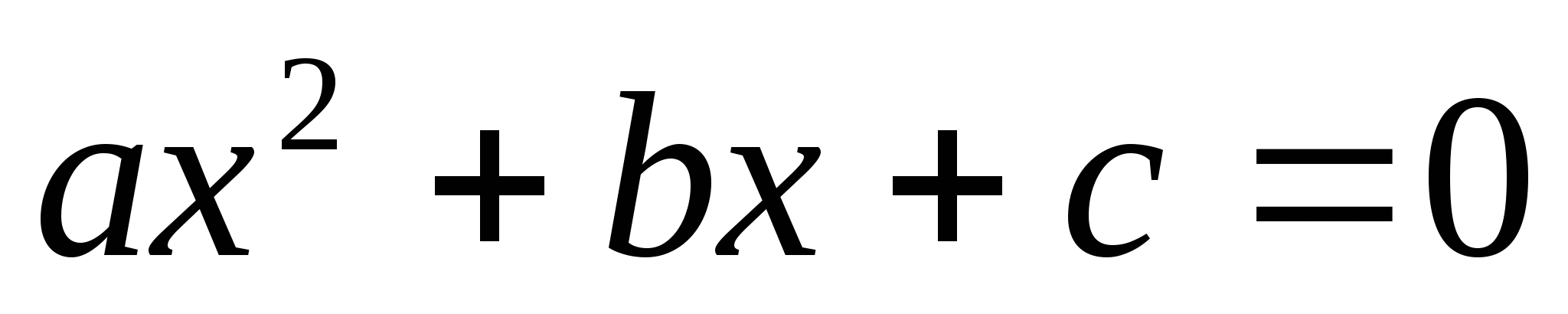 , где a,
b, c - заданные числа, a
, где a,
b, c - заданные числа, a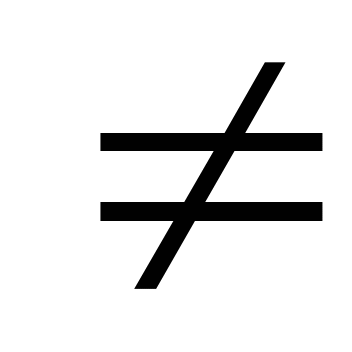 0, x -
переменная, называется...
0, x -
переменная, называется...
-
Полное квадратное уравнение не имеет корней, если D ...
-
Уравнение вида
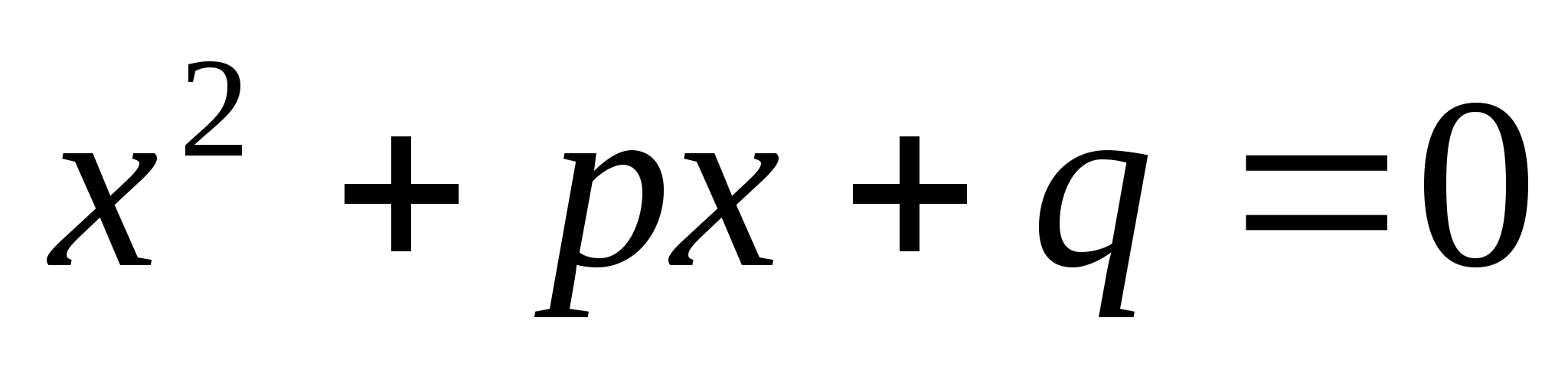 называется ...... квадратным уравнением
называется ...... квадратным уравнением
4. Квадратное уравнение имеет два корня,
если![]() ...
...
5. Дано уравнение ![]() . D =...
. D =...
6. Найдите корни уравнения: 3x² - 5x +2 = 0
Карточки с заданиями, где нужно заполнить пропущенные слова. Ф.И.___________________
II ВАРИАНТ
-
Если
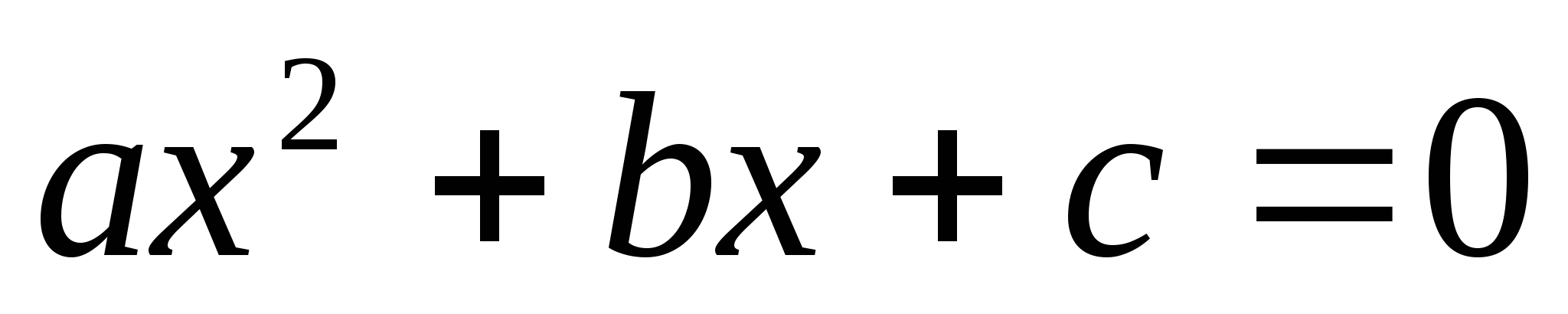 квадратное уравнение, то a... коэффициент, с...
квадратное уравнение, то a... коэффициент, с...
-
Уравнение x² = a, где a < 0, не имеет...
-
Полное квадратное уравнение имеет единственный корень, если
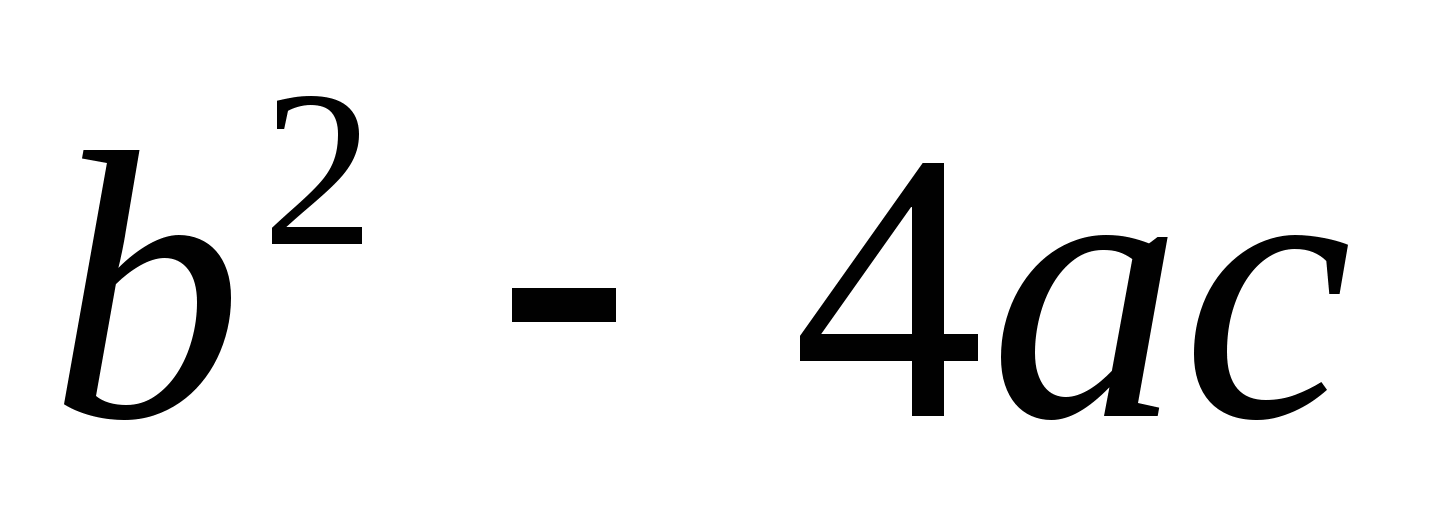 ...
...
-
Уравнение вида ax² + c = 0, где a
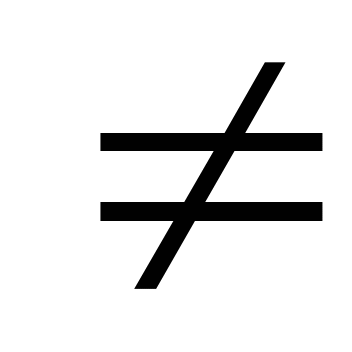 0, c
0, c
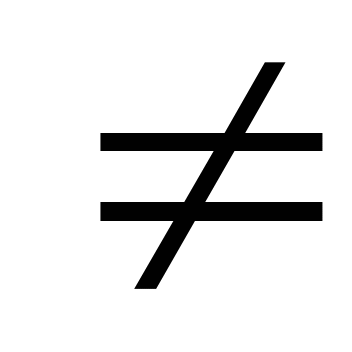 0,
называют ….. квадратным уравнением.
0,
называют ….. квадратным уравнением.
-
Дано уравнение x²- 6x + 8 = 0. D =...
-
Найдите корни уравнения: 2x² - 5x +3 = 0
Решите уравнения в парах:
1. x²- 8x + 15 = 0 4. x² - 11x + 18 = 0
2. x² - 5x - 6 = 0 5. x² - 4x + 4 = 0
3. 3x² + 4x + 20 = 0 6. 5x² - 3x - 2 = 0
Решите уравнения в парах:
1. x²- 8x + 15 = 0 4. x² - 11x + 18 = 0
2. x² - 5x - 6 = 0 5. x² - 4x + 4 = 0
3. 3x² + 4x + 20 = 0 6. 5x² - 3x - 2 = 0
Решите уравнения в парах:
1. x²- 8x + 15 = 0 4. x² - 11x + 18 = 0
2. x² - 5x - 6 = 0 5. x² - 4x + 4 = 0
3. 3x² + 4x + 20 = 0 6. 5x² - 3x - 2 = 0
Решите уравнения в парах:
1. x²- 8x + 15 = 0 4. x² - 11x + 18 = 0
2. x² - 5x - 6 = 0 5. x² - 4x + 4 = 0
3. 3x² + 4x + 20 = 0 6. 5x² - 3x - 2 = 0
Решите уравнения в парах:
1. x²- 8x + 15 = 0 4. x² - 11x + 18 = 0
2. x² - 5x - 6 = 0 5. x² - 4x + 4 = 0
3. 3x² + 4x + 20 = 0 6. 5x² - 3x - 2 = 0
Решите уравнения в парах:
1. x²- 8x + 15 = 0 4. x² - 11x + 18 = 0
2. x² - 5x - 6 = 0 5. x² - 4x + 4 = 0
3. 3x² + 4x + 20 = 0 6. 5x² - 3x - 2 = 0
Решите уравнения в парах:
1. x²- 8x + 15 = 0 4. x² - 11x + 18 = 0
2. x² - 5x - 6 = 0 5. x² - 4x + 4 = 0
3. 3x² + 4x + 20 = 0 6. 5x² - 3x - 2 = 0