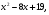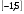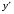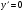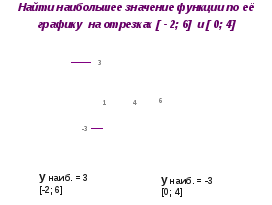Методическая разработка учебного занятия по дисциплине «Математика»

Министерство образования и науки Челябинской области

государственное бюджетное образовательное учреждение

среднего профессионального образования

(среднее специальное учебное заведение)

«Южно-Уральский многопрофильный колледж»

Методическая разработка

учебного занятия по дисциплине «Математика»

(специальность 21.02.05 Земельно-имущественные отношения)

Раздел 1. Начала математического анализа

Тема 2.2 Производная

Тема занятия Нахождение наибольшего и наименьшего значения функции

г. Челябинск, 2015

О Д О Б Р Е Н О

Цикловой методической комиссией естественнонаучных дисциплин

Протокол № 9

« 28 » мая 2015 г.

Председатель ЦМК

_____________О.Н. Суханова

Составитель: М.А. Вуйлова, методист, преподаватель математики высшей категории ГБОУ СПО (ССУЗ) «Южно-Уральский многопрофильный колледж»

Рецензент: Е.А.Кондратьева, преподаватель математики высшей категории ГБОУ СПО (ССУЗ) «Южно-Уральский многопрофильный колледж»

Данная методическая разработка предназначена для преподавателя в разработке структуры и методики изложения учебного материала по данной теме.

Многие схемы, таблицы и иллюстрации могут быть использованы в качестве раздаточного материала, при организации самостоятельной работы студентов и на практических занятиях.

Методическая разработка может быть использована для изучения указанной в нем темы студентами дневного и заочно отделения по специальности 21.02.05 Земельно-имущественные отношения, при подготовке к учебным занятиям и для самостоятельной внеаудиторной работы.

План учебного занятия

Тема: «Нахождения наибольшего и наименьшего значения функции»

Тип учебного занятия: комбинированный урок

Методы обучения: 1. Репродуктивный.

2. Информационно - рецептивный.

3. Частично - поисковый.

Цели учебного занятия:

1. Учебная: формирование знаний:

- о применении производной для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке,

- о нахождении наибольшего и наименьшего значения функции на незамкнутом промежутке

- о математической модели решения задач на оптимизацию

формирование умений:

- применять производную для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке

- применять производную для нахождения наибольшего и наименьшего значения функции на незамкнутом промежутке

- применять математическую модель при решении задач на оптимизацию.

формирование общих компетенций:

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 3. Организовывать свою собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.

ОК 5. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.

ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.

2. Развивающая: Развитие внимания, памяти, речи; развитие функций мышления (анализ, синтез, сравнение, классификация, установление причинно - следственных связей, обобщение)

3. Воспитательная: Воспитание аккуратности, ответственности при выполнении работы, самостоятельности, интереса к изучаемой дисциплине.

План содержания учебного занятия:

1.. Нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке

Знания: о применении производной для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке.

Умения: применять производную для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке.

2. Нахождения наибольшего и наименьшего значений функции на незамкнутом промежутке.

Знания: о нахождении наибольшего и наименьшего значения функции на незамкнутом промежутке.

Умения: применять производную для нахождения наибольшего и наименьшего значения функции на незамкнутом промежутке.

3. Задачи на оптимизацию.

Знания: о математической модели решения задач на оптимизацию.

Умения: применять математическую модель при решении задач на оптимизацию.

Средства обучения:

Презентация «Нахождения наибольшего и

наименьшего значений функции», плакат,

раздаточный материал.

План учебного занятия:

1. Организация группы.(1 мин).

2. Целеполагание и мотивация.(2 мин).

3. Актуализация опорных знаний (5 мин).

3.1 Работа со схемой

3.2 Устная работа

4. Работа по теме учебного занятия. (13 мин).

5. Закрепление изученного материала. (20 мин).

   1. Совместный разбор задачи

   2. Самостоятельное решение задачи

6. Подведение итогов учебного занятия (3 мин.)

7. Домашнее задание (1 мин).

Ход учебного занятия:

№

п/п

Содержание и структура

Учебного занятия

Вре-мя

(мин)

Деятельность

преподавателя

Деятельность

обучающихся

Слайды

презентации

1.

Организация группы.

1

Слушает раппорт, проверяет явку и готовность обучающихся к учебному занятию.

Дежурные сообщают об отсутствующих на занятии.

2.

Целеполагание, мотивация.

-может ли функция принимать наибольшее и наименьшее значения на отрезке?

- в каких точках функция может принимать

наибольшее и наименьшее значения?

Проблемная ситуация.

- может ли функция иметь наибольшее и наименьшее значения на незамкнутом промежутке?

Сформулируйте цели нашего занятия.

2

Организует совместное целеполагание и мотивацию на основе репродуктивного метода.

Управляет познавательной деятельностью обучающихся с помощью наводящих вопросов.
Уточняет ответы обучающихся,

и помогает им грамотно сформулировать тему и цели учебного занятия.

Пытаются ответить на поставленные вопросы, высказывают собственные суждения, делают выводы.

Совместно с преподавателем формулируют тему и цели урока.

Осмысливают и принимают цели данного занятия..

Слайд 1-2

3.

Актуализация опорных знаний.

Обучающиеся работают со схемой.

Устные задания обучающимся:

-Найти наибольшее значение функции по её графику на отрезках [ - 2; 6] и [ 0; 4]

-Найти наименьшее значение функции по её графику на отрезках [ - 8; 0] и [ - 2; 3]

-Повторите и озвучьте этапы нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке

- Задание обучающимся

Работа парами. Схема

Найдите наибольшее и наименьшее значение функции на отрезке.

у = 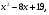на отрезке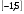

Объяснение преподавателя с привлечением учащихся

5

Организует актуализацию опорных знаний обучающихся группы с целью повторения пройденного материала на основе репродуктивного метода.

Управляет познавательной деятельностью обучающихся, уточняет их ответы, и помогает им грамотно сформулировать информацию - ответы на поставленные вопросы.

Устно отвечают на вопросы преподавателя.

Вспоминают,
воспроизводят
и анализируют
ранее изученную информацию,
отвечая на поставленные вопросы.

(ОК 3 - организуют собственную деятельность исходя из цели и способов ее достижения, определенных руководителем)

Слушают ответы других обучающихся, дополняют и уточняют их.

Слайд 3-4- задание

Слайд 5

Слайд 6-7

4.

Работа по теме учебного занятия.

13

4.1.

4.2

Понятие о нахождении наибольшего и наименьшего значения функции на незамкнутом промежутке.

Задание обучающимся

- Работа с раздаточным материалом

Раздаточный материал.

Отыскание наибольшего и наименьшего значения непрерывной функции на промежутке.

Случай незамкнутого промежутка.

Простейшие случаи:

1.Если непрерывная функция у = f (х) имеет в промежутке только одну точку экстремума х₀ и эта точка максимума, то функция в точке х₀ принимает наибольшее значение.

2.Если непрерывная функция у = f (х) имеет в промежутке только одну точку экстремума х₀ и эта точка минимума, то функция в точке х₀ принимает наименьшее значение.

Объяснение преподавателя с привлечением обучающихся

-на практике часто приходится решать задачи на оптимизацию (оптимизация означает наилучший).

Такие задачи решаются на производстве при вычислении выпуска наибольшего количества продукции, при изготовлении тары большей вместимости, при планировании связи предприятия с источником сырья так, чтобы транспортные расходы оказались минимальными и т. д.

Понятие о математической модели решения задач на оптимизацию

- задачи на оптимизацию решают по схеме:

1. составление математической модели.

2. работа с моделью.

3. ответ на вопрос задачи.

Организует работу обучающихся по усвоению нового материала.

Постановка вопроса - темы для обсуждения.

Демонстрации презентации для иллюстрации изучаемого материала.

Организация поиска ответа на поставленное задание с применением частично - поискового метода.

Проводит изложение нового материала в форме эвристической беседы с использованием слайдов презентации.

Пытаются ответить на поставленный вопрос, используя жизненный опыт и знания, полученные ранее.

Воспринимают, осмысливают информацию, устанавливают причинно-следственные связи.

Применяют операции сравнения, систематизации и классификации при выполнении поставленного задания.

(ОК 3 - организуют собственную деятельность исходя из цели и способов ее достижения, определенных руководителем)

Слайды 8

Слайд 9

5

5.1

Закрепление изученного материала.

-Совместный разбор задачи.

Карточка

Периметр основание лотка для перевозки хлеба составляет 260 см. Каковы должны быть его стороны, чтобы площадь основания была наибольшей?

Решение.

р=260.

Р=2(а + в); 2(а + в) = 260; (а + в) = 130.

Пусть а = х, тогда в = 130 - х.

S = ав; S = х(130 - х) х(0; )

1. Д(S)=R

2.

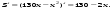
3. 130 − 2x = 0; 2х=130; х = 65.

а = 65; в = 65

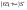>0; < 0

x = 65. S = 65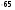=4225. Max S при а=в=65.

S = 4225 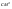= 0,4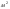

Ответ: а=в =65см.

20

Организация поиска ответа на поставленное задание с применением частично - поискового метода.

Организует обсуждение итогов работы, уточняет и дополняет ответы обучающихся.

Под руководством преподавателя анализируют информацию, проводят ее синтез, сравнивают, делают выводы. Ведут записи в тетрадях.

По итогам задачи делают вывод.

Слайды
10

5.2

-Задания обучающимся

Самостоятельный разбор по схеме и оформление задачи (обучающиеся работают парами)

Площадь основания ротационной печи камерного типа равна 4 м². Каковы должны быть размеры площади основания печи, чтобы периметр основания был наименьшим?

Решение.

S =4. S = ав; ав = 4.

Пусть а = х, тогда в =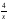

р = 2(х + 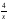) х(0; )

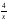= 2 −

1.Д (р)=R, кроме х = 0

2 − = 0; = 2; = 4; х = 2.

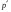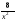< 0; <0

х =2. а = 2, в = 2

min р = 2(2+2) =8.

Ответ: а = 2м, в = 2м.

Управляет познавательной деятельностью обучающихся, оказывает

дозированную помощь

Организует обсуждение итогов работы, уточняет и дополняет ответы обучающихся.

Применяют операции анализ, синтез, сравнение при выполнении поставленного задания.

ОК 6 - работа в коллективе, эффективное общение с коллегами.

Слайд

11-12

7.

Подведение итогов

урока.

Удалось ли нам достичь поставленных целей учебного занятия?

Что нового вы сегодня узнали?

Какие затруднения у вас были в работе?

3

Подведение итогов урока в соответствии с поставленными целями урока.

Организует обсуждение итогов занятия, его результативности.

Сообщение оценок, поставленных за занятие.

Участвуют в совместном подведении итогов,
рефлексия.

Слайд 13

8.

Домашнее

задание.

1

§6 п.25 стр. 155.

Задача № 317 стр. 159

Фиксируют домашнее задание.

Задают вопросы по неясным моментам.

Слайд 13

Приложение 1

Схема нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке

Этапы

Пример для функции

у = 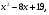на отрезке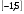

1. Найти область определения функции.

D( у) =

2. Найти производную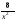

.

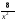3. Найти на данном отрезке критические точки, т. е. точки, в которых 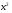= 0 или не существует.

D (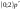) = R.

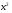= 0

4. Вычислить значения функции в критических точках и на концах отрезка.

у( ) =

у( ) =

у( ) =

5. Из вычисленных значений выбрать наименьшее и наибольшее.

max у(x) = у( ) =

min у(x) = у( ) =

__________________________________________________________________________________

Отыскание наибольшего и наименьшего значения непрерывной

функции на промежутке.

Случай незамкнутого промежутка.

Непрерывная функция на незамкнутом промежутке может иметь и может не иметь у_max., у_min.

Простейшие случаи:

Если непрерывная функция у = f (х) имеет в промежутке только одну точку экстремума х₀ и если х₀ - точка максимума, то f (х₀) = у_max.

Если непрерывная функция у = f (х) имеет в промежутке только одну точку экстремума х₀ и если х₀ - точка минимума, то f (х₀) = у_min.

Приложение 2