Исследовательская работа на тему Бином Ньютона

Министерство образования, науки и молодежи Республики Крым

Малая академия наук Крыма «Искатель»

Отделение: математика

Секция: математическое моделирование

Бином Ньютона

Работу выполнил

_______________________

ученик ____ класса

Научный руководитель

СОДЕРЖАНИЕ

ВВЕДЕНИЕ………………………………………………………………………….3

РАЗДЕЛ 1. ФОРМУЛА БИНОМА НЬЮТОНА…………………………………..4

1.1. Сочетания и их свойства……………………………………………………….4

1.2. Вывод формулы бинома Ньютона ……………………………………………6

1.3. Треугольник Паскаля…………………………………………………………...9

1.4. Полиномиальная теорема……………………………………………………...15

1.5. Применение бинома Ньютона к решению задач.…………………………….17

1.6. Применение формулы бинома Ньютона к приближенным вычислениям…18

РАЗДЕЛ 2. ФОРМУЛЫ СУММЫ И РАЗНОСТИ СТЕПЕНЕЙ…………………20

2.1. Вывод формул с помощью ММИ……………………………………………..20

2.2. Теорема Безу и ее следствия ………………………………………………….21

ЗАКЛЮЧЕНИЕ……………………………………………………………………..25

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………………….26

ПРИЛОЖЕНИЯ……………………………………………………………………..27

ВВЕДЕНИЕ

О биноме Ньютона речь идет в романе «Последнее дело Холмса» Конан Дойля. Это же выражение упомянуто в фильме «Сталкер» А.А.Тарковского. Бином Ньютона упоминается в фильме «Расписание на послезавтра», в повести Льва Толстого «Юность» в эпизоде сдачи вступительных экзаменов в университет Николаем Иртеньевым и в романе Замятина «Мы».

Когда хотят подчеркнуть, что собеседник преувеличивает сложность задач, с которыми он столкнулся, говорят: «Тоже мне бином Ньютона!» Дескать, вот бином Ньютона, это сложно, а у тебя какие проблемы! О биноме Ньютона слышали даже те люди, чьи интересы никак не связаны с математикой.

Слово «бином» означает двучлен, т.е. сумму двух слагаемых. Из школьного курса известны так называемые формулы сокращенного умножения:

(а + b)² = a² + 2ab + b², (a + b)³ = a³ +3a²b + 3ab² + b³.

Обобщением этих формул является формула, называемая формулой бинома Ньютона. Используются в школе и формулы разложения на множители разности квадратов, суммы и разности кубов. Имеют ли они обобщение для других степеней? Да, есть такие формулы, они часто используются в решении различных задач: на доказательство делимости, сокращение дробей, приближенные вычисления.

Изучение обобщающих формул развивает дедуктивно-математическое мышление и общие мыслительные способности.

Объекты исследования: бином Ньютона, формулы суммы и разности степеней.

Цель исследования: обобщить формулы сокращенного умножения, показать их применение к решению задач.

Задачи исследования: 1) изучить и систематизировать информацию по данному вопросу; 2) привести примеры задач на применение бинома Ньютона и формул суммы и разности степеней.

РАЗДЕЛ 1

ФОРМУЛА БИНОМА НЬЮТОНА

1. Сочетания и их свойства

Пусть X - множество, состоящее из n элементов. Любое подмножество Y множества X, содержащее k элементов, называется сочетанием k элементов из n, при этом, k ≤ n.

Число различных сочетаний k элементов из n обозначается С_n^k . Одной из важнейших формул комбинаторики является следующая формула для числа С_n^k :

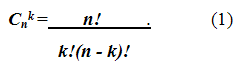
Её можно записать после очевидных сокращений следующим образом:

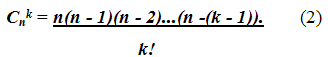
В частности,

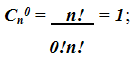
Это вполне согласуется с тем, что в множестве X имеется только одно подмножество из 0 элементов - пустое подмножество.

Числа C_n^k обладают рядом замечательных свойств.

Справедлива формула

С_n^k = С^n-k_n , (3)

Смысл формулы (3) состоит в том, что имеется взаимно-однозначное соответствие между множеством всех k-членных подмножеств из X и множеством всех (n - k)-членных подмножеств из X: чтобы установить это соответствие, достаточно каждому k-членному подмножеству Y сопоставить его дополнение в множестве X.

Справедлива формула С⁰_n + С¹_n + С²_n + … + Сⁿ_n = 2ⁿ (4)

Сумма, стоящая в левой части, выражает собой число всех подмножеств множества X (C⁰_n есть число 0-членных подмножеств, C¹_n - число одночленных подмножеств и т.д.).

При любом k, 1≤ k≤ n , справедливо равенство

C^k_n = C_n-1^k + C_n-1^k-1 (5)

Это равенство нетрудно получить с помощью формулы (1). В самом деле,

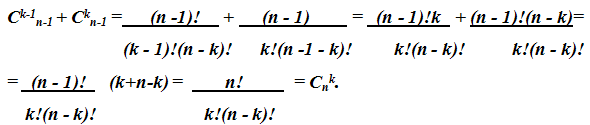
Пример. Вычислить C₈³.

Решение.

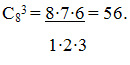
Пример.

Вычислите С₁₇² - С₁₅².

Решение.

Пример. Решите уравнения:

а) С_x³ = 2∙C_x²;

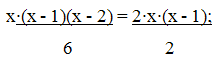
x - 2 = 6;

x = 8.

b) C_x^x-2 = 15;

C_x^x-2 = C_x^x-x+2 = C_x²;

x∙(x - 1) = 30 = 6∙5;

x = 6.

c) C_x² + C_x+1² = 49;

x∙(x - 1) + (x + 1)∙x = 98;

x² = 49; x є N;

x = 7.

d) 13C_2nⁿ⁺¹ = 7C_2n+1^n-1; n є N.

13C_2n^n-1 = 7C_2n+1^n-1

13·(n + 2) = 7·(2n + 1),

отсюда n = 19. [1,3]

1.2. Вывод формулы бинома Ньютона

Рассмотрим степени двучлена а + b.

n = 0, (а +b)⁰ = 1

n = 1, (а +b)¹ = 1а+1b

n = 2, (а + b)² = 1а²+ 2аb +1b²

n = 3, ( а + b)³ = 1 а³ + 3а²b + 3аb²+1 b³

n = 4, ( а + b)⁴ = 1а⁴ + 4а³b + 6а²b²+4а b³ +1b⁴

n = 5, (а + b)⁵ = 1а⁵+ 5а⁴b+ 10а³b²+ 10а²b³+ 5аb⁴+ 1b⁵

Заметим следующие закономерности:

- число членов получаемого многочлена на единицу больше показателя степени бинома;

- показатель степени первого слагаемого убывает от n до 0, показатель степени второго слагаемого возрастает от 0 до n;

- степени всех одночленов равны степени двучлена в условии;

- каждый одночлен является произведением первого и второго выражения в различных степенях и некоторого числа - биноминального коэффициента;

- биноминальные коэффициенты, равноотстоящие от начала и конца разложения, равны.

Обобщением этих формул является следующая формула, называемая формулой бинома Ньютона:

(a + b)ⁿ = C⁰_n aⁿb⁰+ C¹_n a^n-1b + C²_n a ^n-2b² + ... + C^n-1_n ab^n-1 + Cⁿ_n a⁰bⁿ. (6)

В этой формуле n может быть любым натуральным числом. [2]

Выведем формулу(6). Прежде всего, запишем:

(a + b)ⁿ = (a + b)(a + b) ... (a + b), (7)

где число перемножаемых скобок равно n. Из обычного правила умножения суммы на сумму вытекает, что выражение (7) равно сумме всевозможных произведений, которые можно составить следующим образом: любое слагаемое первой из сумм а + b умножается на любое слагаемое второй суммы a +b, на любое слагаемое третьей суммы и т.д. Hапример, при n = 3 имеем:

(a +b)(a + b)(a + b) = aaa + aab + aba + abb + baa + bab + bba + bbb.

Из сказанного ясно, что слагаемым в выражении для (a + b)ⁿ соответствуют (взаимно-однозначно) строки длиной n, составленные из букв а и b. Среди слагаемых будут встречаться подобные члены; очевидно, что таким членам соответствуют строки, содержащие одинаковое количество букв а. Но число строк, содержащих ровно k раз букву а, равно С_n^k. Значит, сумма всех членов, содержащих букву а множителем ровно k раз, равна С_n^k a ^n-kb^k. Поскольку k может принимать значения 0, 1, 2, …, n-1, n, то из нашего рассуждения следует формула (6). Заметим, что (6) можно записать короче:

(8)

Хотя формулу (6) называют именем Ньютона, в действительности она была открыта ещё до Ньютона (например, её знал Паскаль). Заслуга Ньютона состоит в том, что он нашёл обобщение этой формулы на случай не целых показателей. Именно И.Ньютон в 1664-1665 гг. вывел формулу, выражающую степень двучлена для произвольных дробных и отрицательных показателей.

Числа С⁰_n, C¹_n, ..., Cⁿ_n, входящие в формулу (6), принято называть биномиальными коэффициентами, которые определяются так:

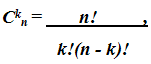
Из формулы (6) можно получить целый ряд свойств этих коэффициентов. Например, полагая а =1, b = 1, получим:

2ⁿ = C⁰_n + C¹_n + C²_n + C³_n + ... +Cⁿ_n,

т.е. формулу (4). Если положить а = 1, b = -1, то будем иметь:

0 = С⁰_n - C¹_n + C²_n - C³_n + ... + (-1)ⁿCⁿ_n

или С⁰_n + C²_n + C⁴_n + ... = C¹_n + C³_n + + C⁵_n + ... .

Это значит, что сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна 2^n-1.

Коэффициенты членов, равноудалённых от концов разложения, равны. Это свойства следует из соотношения: С_n^k = С_n^n-k

Интересен частный случай

(x + 1)ⁿ = C⁰ _nxⁿ + C¹_n x^n-1 + ... + C^k_n x^n-k + ... + Cⁿ_n x⁰

или короче

(x +1)ⁿ = ∑C_n^k x^n-k.

Примеры. Найти разложение бинома

а) (a+b)⁴ =C⁰₄a⁴b⁰ +C¹₄a³b¹ + C²₄a²b² + C³₄a¹b³ +C⁴₄a⁰b⁴ =a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

б) (х +у)⁵ = х⁵ + 5х⁴у + 10х³у² + 10х²у ³+ 5ху⁴ + у⁵

в) (1 + 2а)⁴ = 1⁴ + 4·1³·2а + 6·1²·(2а)² + 4· 1¹·(2а)³ + (2а)⁴ =

=1 + 8а + 24а² + 32а³ + 16а⁴

г) (х - у)⁶ = (х + (-у))⁶ = х⁶ + 6х⁵(-у) + 15х⁴(-у)² + 20х³(-у)³ +

+15х²(-у)⁴ + 6х(-у)⁵ + у⁶= х⁶- 6х⁵у +15х⁴у²- 20х³у³ + 15х²у⁴ - 6ху⁵+ у⁶

д) Решить уравнение

Решение. Осуществим замену:

Тогда уравнение перепишем:

Применим формулу бинома к левой части уравнения:

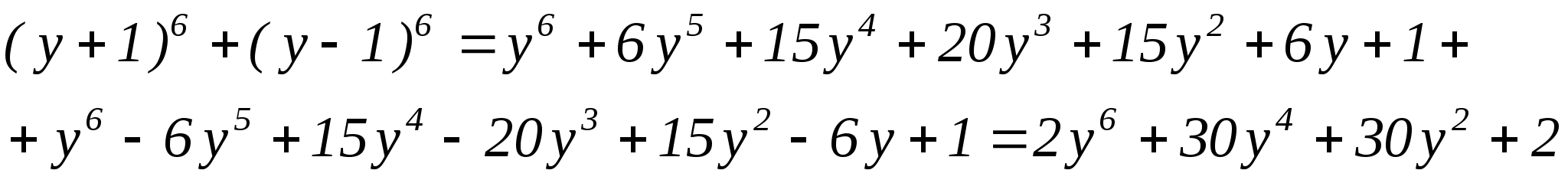
В итоге 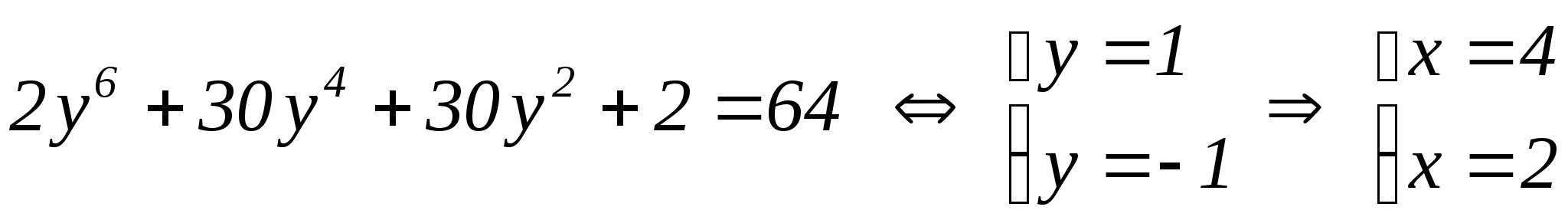Ответ: . [5]

1.3. Треугольник Паскаля

Равенство (5) позволяет вычислять значения C_n^k, если известны С_n-1^k и С _n-1^k-1. Иными словами, с помощью этого равенства можно последовательно вычислять С_n^k сначала при n = 1, затем при n = 2, n = 3 и т.д. Вычисления удобно записывать в виде треугольной таблицы:

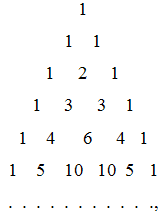
в (n + 1) строке которой по порядку стоят числа С⁰_n, С¹_n, …, Сⁿ_n . При этом крайние числа строки, т.е. С⁰_n и Сⁿ_n , равны 1, а остальные числа находятся по формуле (5). Поскольку С_n-1^k-1 и С_n-1^k распологаются в этой таблице строкой выше, чем число С_n^k, и находятся в этой строке слева и справа от него, то для получения числа С_n^k надо сложить находящиеся слева и справа от него числа предыдущей строки. Например, число 10 в шестой строке мы получаем, сложив числа 4 и 6 пятой строки. Указанная таблица и является "арифметическим треугольником Паскаля".

Блез Паскаль прожил 39 лет, но, несмотря на столь короткую жизнь, он вошел в историю как выдающийся математик, физик, философ и писатель. Его именем благодарными потомками названы единица давления (паскаль) и получивший чрезвычайно широкое распространение язык программирования. Но, наверное, самой известной математической работой Блеза Паскаля является "Трактат об арифметическом треугольнике", образованном биноминальными коэффициентами, который имеет применение в теории вероятностей, комбинаторике, математическом анализе, теории чисел и обладает удивительными и занимательными свойствами.

Коэффициент в разложении (a + b)ⁿ при a^n-kb^k обозначается С_n^k. Можно вычислить все биномиальные коэффициенты для любого n путём непосредственного перемножения n множителей (a + b), раскрытия скобок и приведения подобных членов. Правда, математикам древности и среднековья сделать это мешало отсутствие алгебраической символики. Например, в одном средневековом математическом тексте, имевшем хождение в Западной Европе в XV в. и, по-видимому, восходящем к арабам, биномиальные коэффициенты вычисляются очень наглядно путём возведения в степени числа 10001 и приводятся в виде таблицы.

Таблица 1.

Степень числа 10001, воспроизводящая биномиальные коэффициенты

Ат-Тутси (XIII в.) располагал таблицей биномиальных коэффициентов и привёл общее правило для их получения, которое в современных обозначениях может быть выражено так: C^k_n = C_n-1^k + C_n-1^k-1

Благодаря данному правилу можно вычислять биномиальные коэффициенты последовательно для всех больших степеней n: а именно, k-й коэффициент бинома степени n равен сумме k-го и (k-1)-го коэффициентов степени (n-1). К этому следует добавить, что в биноме степени n первый (точнее, нулевой, k = 0) и последний (k = n) коэффициенты - т.е. коэффициенты при aⁿ и при bⁿ - оба равны 1 (при перемножении n множителей (a + b) член aⁿ получается единожды, а именно, при перемножении n раз чисел a; то же верно и для члена bⁿ).

Если записать биномиальные коэффициенты n в виде таблицы со строками n и столбцами k, то каждая строка будет начинаться и заканчиваться единицей, а каждое промежуточное число строки будет равняться сумме двух чисел предыдущей строки - того, что стоит непосредственно над ним, и то, что стоит левее.

Таблица 2.

Биномиальные коэффициенты

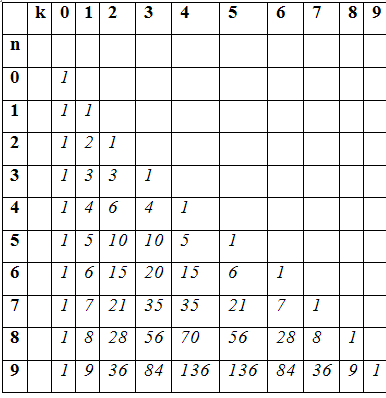
Нетрудно видеть, что каждая строка данной таблицы симметрична, т.к. коэффициенты при a^kb^n-k и a^n-kb^k в разложении бинома совпадают. Полученный числовой треугольник называется треугольником Паскаля. Таблицы биномиальных коэффициентов были известны и предшествующим математикам - китайским, арабским и европейским (П. Аппиан, 1527 г.; М. Штифель, 1544 г.; Н. Тарталья, 1556 г.). Однако именно благодаря работе Паскаля "Тракт об арифметическом треугольнике", опубликованной уже после смерти автора (в 1665 г.), свойства биномиальных коэффициентов получили широкую известность. Правда, сам Паскаль (и многие его предшественники) рисовали этот треугольник несколько иначе, с "повышенными" столбцами и прямым углом при вершине:

Таблица 3.

Треугольник Паскаля

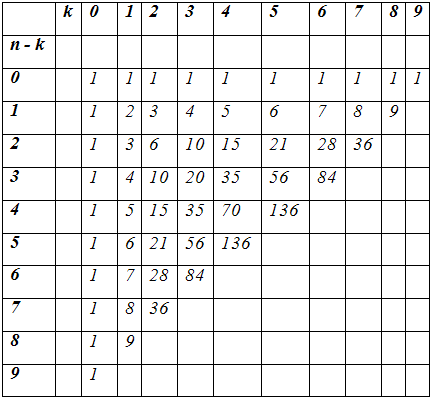
В такой таблице числа, соответствующие разложению бинома степени n, стоят не вдоль одной и той же строки, а вдоль одной и той же восходящей диагонали. Все восходящие диагонали, а значит, и вся таблица симметрична относительно главной нисходящей диагонали - "биссектрисы прямого угла". Каждое число в таблице (кроме единиц, находящихся на верхнем и левом краях), равняется сумме двух чисел, стоящих от него сверху и слева.

Интересно свойство делимости чисел, составляющих треугольник Паскаля. Если обозначить одним цветом числа, делящиеся нацело на какое-нибудь натуральное число, а другим - делящиеся с остатком, получается неожиданные узоры. Некоторые из них составлены из равных разноцветных треугольников - это результат деления на простые числа. Другие же похожи на фракталы (см. приложения).

Числа, стоящие вдоль одной и той же строки (столбца) в таблице, так же интересны. То, что в нулевой строке и нулевом столбце стоят единицы, очевидно. Очевидно и то, что в первой строке и первом столбце стоят подряд все натуральные числа: 1, 2, 3, 4 и т.д.

А вот что за числа стоят на второй строке (столбце)? Оказывается, эти числа имеют своё название, причём носят его с глубокой древности - это треугольные числа. А числа на третьей строке (столбце) - пирамидальные числа, равные сумме треугольных.

Треугольные и пирамидальные числа

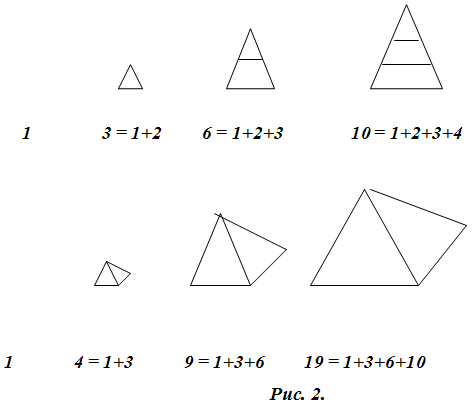
1 4 = 1+3 10 = 1+3+6 20 = 1+3+6+10

Если обратиться к форме треугольник Паскаля, представленный в таблице 2, и рассмотреть её столбцы и нисходящие диагонали, то это рассмотрение ничего не даст: фактически, столбцы у таблиц 2 и 3 одни и те же, а нисходящие диагонали таблицы 2 совпадают со строками таблицы 3. Строки же таблицы 2 совпадают с восходящими диагоналями таблицы 3. Последовательность (1, 1, 2, 3, 5, 8, …), полученная при разборе восходящих диагоналей таблицы 2: 1; 1; 1+1 = 2; 1+2 = 3; 1+3 = 5, 1+3+1 = 5; 1+4+3 = 8 и т.д., обладает тем свойством, что каждое число в ней равно сумме двух предыдущих. Эти числа носят название чисел Фибоначчи и обладают многими интересными математическими свойствами, возникая в самых неожиданных задачах.

Приведём одно из свойств, связанных с делимостью биномиальных коэффициентов. Рассмотрим таблицу 2. Легко видеть, что все числа её 5-й строки, кроме крайних единиц, делятся на 5; все числа 7-й строки, кроме крайних единиц, делятся на 7. Очевидно, у 2-й и 3-й строки есть такое же свойство. А у остальных, легко видеть, такого свойства нет. Что объединяет числа 2, 3, 5 и 7 и отличает их от других чисел первого десятка? Верно, все они простые. Можно доказать, что, действительно, все числа n-ой строки треугольника Паскаля (в форме таблицы 2), кроме крайних единиц, делятся на n тогда и только тогда, когда n простое.

Еще одно красивое свойство треугольника Паскаля (в форме таблицы 2) связано с вопросом, сколько нечётных чисел содержит n-я строка. Оказывается, число этих нечётных чисел всегда равно 2^k, где k - число единиц в двоичной записи числа n.

Еще одно сравнительно недавно обнаруженное свойство треугольника Паскаля, связывающее его с простыми числами (Г.В. Манн, Д. Шенкс, 1972г.). Запишем строки треугольника Паскаля (в форме таблицы 2), каждый раз сдвигая строки вправо на две позиции.

Таблица 4.

Связь ряда простых чисел и треугольника Паскаля

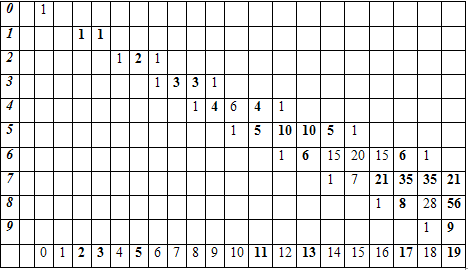
Числа, стоящие в таблице, выделены, если они делятся на номер строки. Числа в нижней строке, нумерующие столбцы, выделены, если в этом столбце все числа выделены. Выходит, что выделенные номера столбцов в точности соответствуют простым числам. [6]

1.4. Полиномиальная теорема

Теорема.

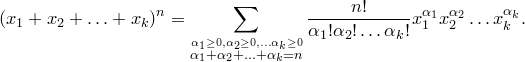
Доказательство.

Чтобы после раскрытия скобок получился одночлен , нужно выбрать те скобок, из которых берется , те скобок, из которых берется и т.д. и те скобок, из которых берется . Коэффициент при этом одночлене после приведения подобных членов равен числу способов, которыми можно осуществить такой выбор. Первый шаг последовательности выборов можно осуществить способами, второй шаг - , третий - и т.д., -й шаг - способами. Искомый коэффициент равен произведению

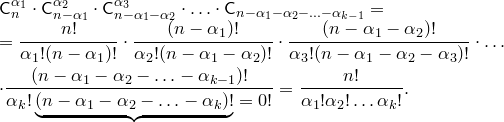
Пример. Раскроем скобки в выражении .

Число 5 можно представить в виде суммы трех целых неотрицательных слагаемых следующими способами:

Заполним следующую табличку. В первом столбце приведены всевозможные разбиения числа 5 на сумму трех слагаемых, второй столбец - коэффициент, который получится при одночлене, третий - вид одночлена (монома), и в скобках указано количество мономов данного вида. Для первого разбиения приведены все мономы данного вида.

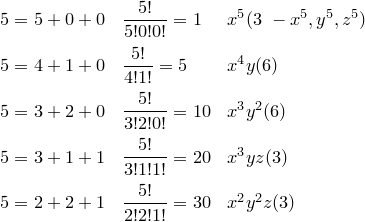
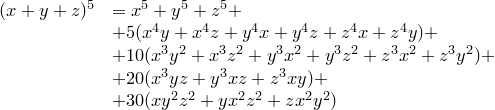
Пример.

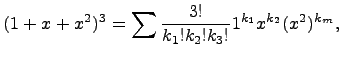
где суммирование производится по всем наборам неотрицательных целых чисел k₁, k₂, k₃, для которых k₁+ k₂+ k₃=3.

Выпишем все такие наборы: (0,0,3), (0,3,0), (3,0,0), (0,1,2), (1,2,0), (2,0,1), (1,0,2), (0,2,1), (2,1,0), (1,1,1). Теперь находим:

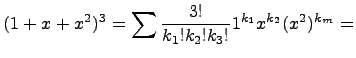
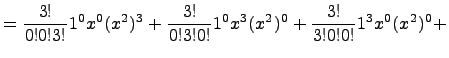
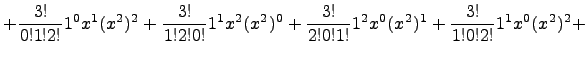
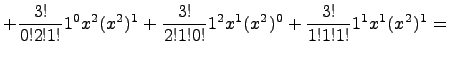
1.5. Применение бинома Ньютона к решению задач

Пример. Найдите коэффициент бинома Ньютона для шестого члена разложения выражения (a+b)¹⁰.

Решение. В нашем примере n=10, k=6-1=5. Таким образом, мы можем вычислить требуемый биномиальный коэффициент:

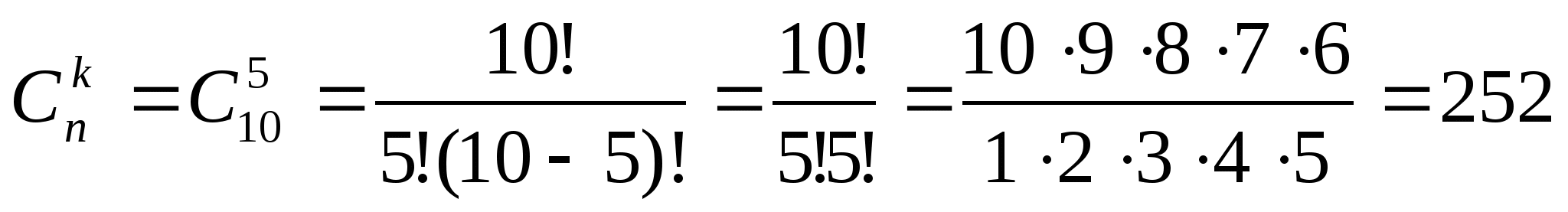
Пример. Найти 13-й член разложения бинома

.

Решение. Согласно формуле общего члена разложения бинома,

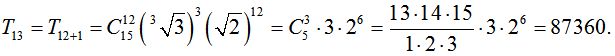
Пример. Найти номер члена разложения бинома

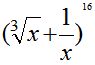, не содержащего х.

Решение. Для общего члена разложения имеем

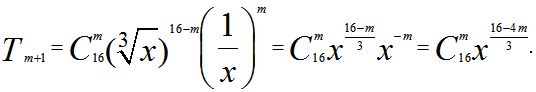
Член разложения не зависит от x; это значит, что показатель степени x равен 0, , 16 - 4m = 0, m = 4.

Итак, пятый член данного разложения не зависит от х.

Примеры, в которых использование бинома Ньютона позволяет доказать делимость выражения на заданное число.

Пример. Доказать, что значение выражения , где n - натуральное число, делится на 16 без остатка.

Решение. Представим первое слагаемое выражение как и воспользуемся формулой бинома Ньютона:

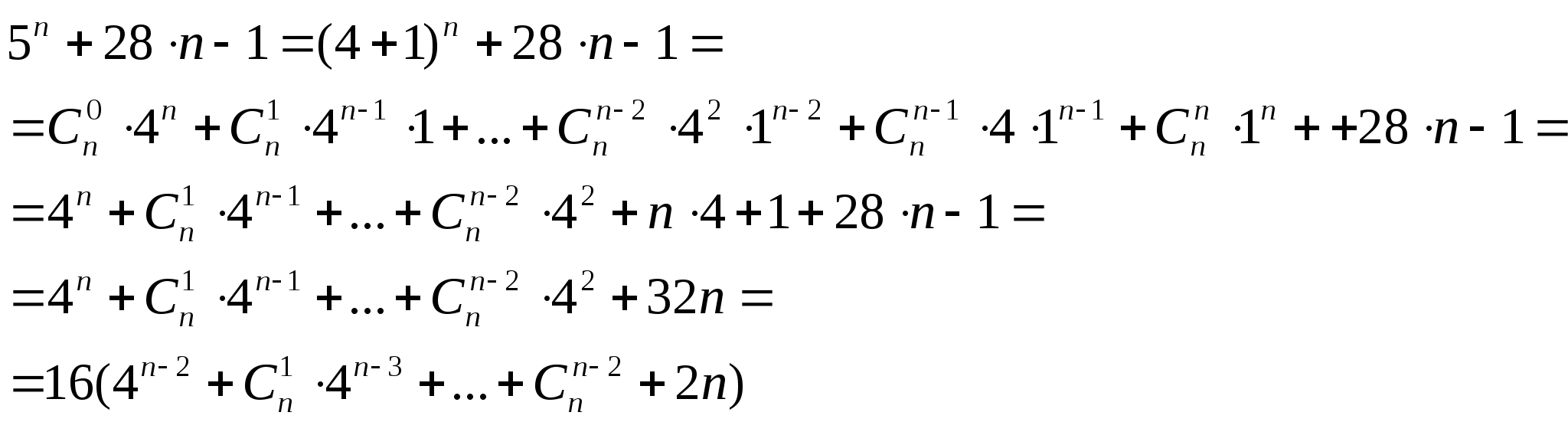
Полученное произведение доказывает делимость исходного выражения на 16.

Пример. Доказать, что число 11¹⁰ - 1 делится на 100.

Решение.

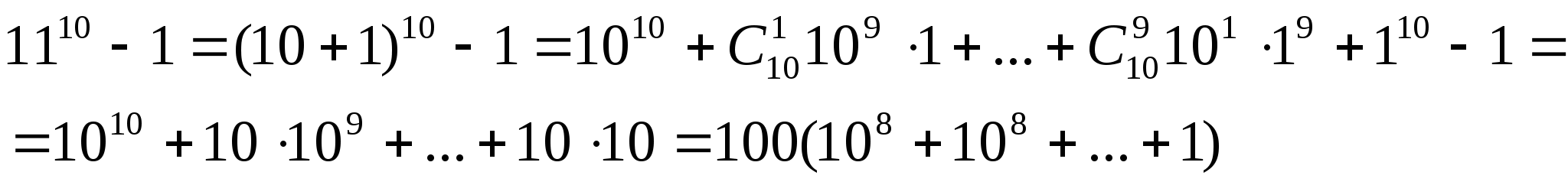
Полученное произведение доказывает делимость исходного выражения на 100.

1.6. Применение формулы бинома Ньютона к приближенным вычислениям

Положив в формуле бинома Ньютона

(a + b)ⁿ = а^п + C_n¹ а^{п- 1} b + C_n² а^{п- 2} b² + ... + C_n^{п- 1} аb^{п- 1} + C_n^п b^п

а = 1, b = х, получим: (1 + х)ⁿ = 1 + C_n¹ х + C_n² х² + ... + C_n^{п- 1} х ^{п- 1} + C_n^п х^п .

Если величина х мала, то величины х², х³, ..., х^п тем более малы. Поэтому если в формуле (1) отбросить члены, содержащие х², х³, ..., х^п, то полученная в результате формула

(1 + х)ⁿ ≈ 1 + C_n¹ х (9)

будет приближенной, причем ошибка такого приближения должна быть небольшой. Поскольку C_n¹ = п, формулу (9) можно переписать в виде:

(1 + х)ⁿ ≈ 1 + n х (10)

Практически при малых значениях х формула (10) дает вполне удовлетворительный результат. В подтверждение этого приведем следующую таблицу для случая х = 0,01.(1 + х)ⁿ

n

По формуле

Значение с четырьмя верными десятичными знаками

2

3

4

10

1,02

1,03

1,04

1,10

1,0201

1,0303

1,0406

1,1046

Формула (10) верна и для малых отрицательных значений х. Например,

(1 - 0,02)⁵ ≈ 1 - 5 ∙ 0,02 = 0,9;

(0,93)² = (1 - 0,07)² ≈ 1 - 2 ∙0,07 = 0,86.

Формулу (10) мы получили для натуральных значений п. На самом же деле ею можно пользоваться при любых действительных значениях п. Например,

√1,003 =(1 +0,003)^½ ≈ 1 + ¹/₂ ∙ 0,003= 1,0015;

³√0,97 = (1 - 0,03)^1/3 ≈ 1- ¹/₃ ∙ 0,03 = 0,99;

¹/_0,98 = 0,98^{- 1} =(1 - 0,02)^{- 1} ≈ 1 + (-1)(-0,02) = 1,02;

РАЗДЕЛ 2

ФОРМУЛЫ СУММЫ И РАЗНОСТИ СТЕПЕНЕЙ

2.1. Вывод формул с помощью ММИ

Из школьного курса известны формулы

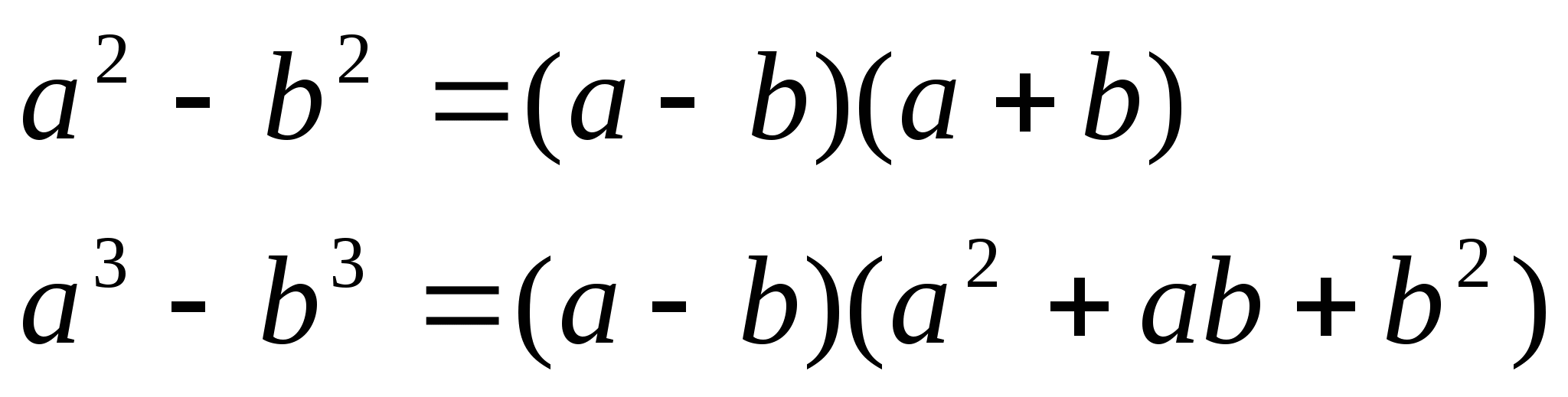
Обобщим эти формулы для любого натурального n (n ≥ 2)

(11)

Доказательство проведем методом математической индукции (ММИ).

Для n=2 равенство верно. Предположим, что равенство верно для некоторого натурального k, т. е. что справедливо:

Проверим для k+1. Преобразуем разность

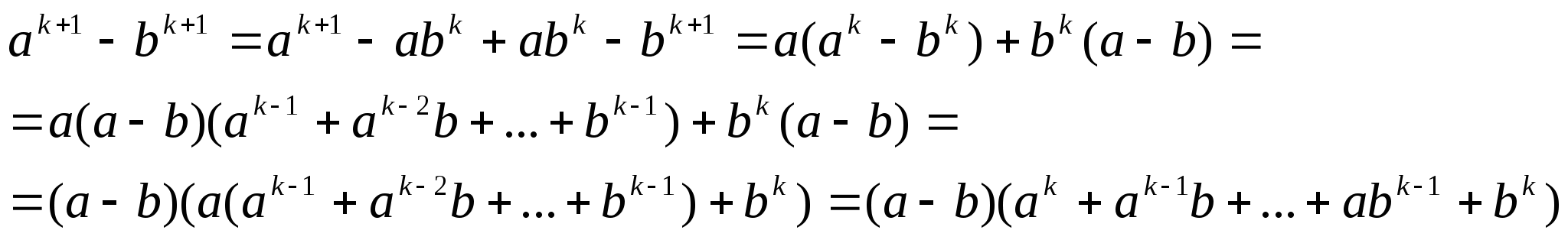
На основании принципа математической индукции это означает, что равенство справедливо для любого натурального числа натурального n (n ≥ 2)

Также справедлива формула

И эта формула имеет обобщение на случай нечетных n:

Для доказательства в формуле (11) обозначим с = - b, тогда для нечетного n

имеем

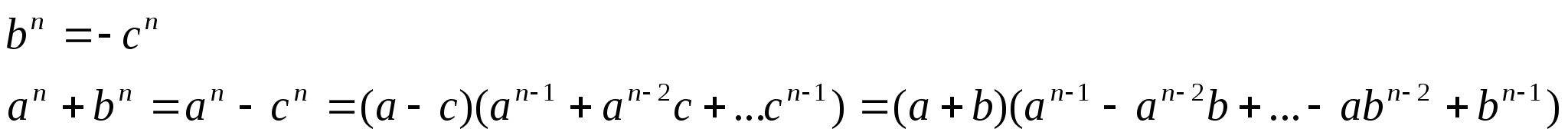Заметим, что для четных n двучлен нельзя разложить в произведение многочленов, один из которых a+b или a-b.

2.2. Теорема Безу и ее следствия

Те же результаты можно получить другим путем - с помощью теоремы Безу.

Теорема Безу. [4] Остаток от деления многочлена Pn(x) на двучлен (x-a) равен значению этого многочлена при x = a.

Пусть Pn(x) - данный многочлен степени n , двучлен (x-a) - его делитель,

Qn-1(x) - частное от деления Pn(x) на x-a (многочлен степени n-1) , R - остаток от деления.

Доказательство:

Согласно правилу деления многочленов с остатком можно записать:

Pn (x) = (x-a)Qn-1(x) + R .

Отсюда при x = a:

Pn (a) = (a-a)Qn-1 (a) + R =0∙Qn-1(a)+R=0+R=R .

Значит, R = Pn (a) , т.е. остаток от деления многочлена на (x-a) равен значению этого многочлена при x=a, что и требовалось доказать.

Следствие 1. Если число a является корнем многочлена P (x) , то этот многочлен делится на (x-a) без остатка.

Доказательство: По теореме Безу остаток от деления многочлена P (x) на x-a равен P (a) , а по условию a является корнем P (x) , а это значит, что P (a) = 0, что и требовалось доказать.

Следствие 2. Если многочлен P (x) имеет попарно различные корни a1 , a2 , … , an , то он делится на произведение (x-a1) … (x-an) без остатка.

Следствие 3. Многочлен степени n имеет не более n различных корней.

Следствие 4. Для любого многочлена P(x) и числа a разность (P(x)-P(a)) делится без остатка на двучлен (x-a) .

Доказательство. Пусть P(x) - данный многочлен степени n , a - любое число .

Многочлен Pn(x) можно представить в виде: Pn(x)=(x-a)Qn-1(x)+R , где Qn-1(x) - многочлен, частное при делении Pn(x) на (x-a), R - остаток от деления Pn(x) на (x-a) . Причём по теореме Безу:R = Pn(a) , т.е. Pn(x)=(x-a)Qn-1(x)+Pn(a) .Отсюда Pn(x) - Pn(a) = (x-a)Qn-1(x) , а это и означает делимость без остатка (Pn(x) - Pn(a) ) на (x-a) , что и требовалось доказать.

Следствие 5. Число a является корнем многочлена P(x) степени не ниже первой тогда и только тогда, когда P(x) делится на (x-a) без остатка.

Следствие 6. Многочлен, не имеющий действительных корней, в разложении на множители линейных множителей не содержит.

На основании теоремы Безу и следствия 5 можно доказать следующие утверждения.

1. Разность одинаковых натуральных степеней на разность их оснований делится без остатка :

Пусть P(x) = xⁿ , P(a) = aⁿ , тогда xⁿ - aⁿ - разность одинаковых натуральных степеней . По следствию 5 P(x) - P(a) = xⁿ - aⁿ = (x - a)Q(x) , а это значит, что (xⁿ-aⁿ)/(x-a)=Q(x), т.е. разность одинаковых натуральных степеней на разность их оснований делится без остатка, что и требовалось доказать .

Итак, (xⁿ - aⁿ)/(x - a) = x^n-1 + ax^n-2 + a²x^n-3 + … +a^n-2x + a^n-1.

2. Разность одинаковых чётных степеней на сумму их оснований делится без остатка.

Пусть P(x) = x^2k , тогда P(a) = a^2k . Разность одинаковых чётных степеней x^2k - a^2k равна P(x) - P(a) . P(a) = a^2k = (-a)^2k = P(-a) , т.е. x^2k - a^2k = P(x) - P(-a).

По следствию 5 P(x) - P(-a) = (x -(- a))Q(x)= (x + a)Q(x), а это значит, что

x^2k - a^2k = (x + a)Q(x) или (x^2k - a^2k)/(x + a) = Q(x) , т.е. разность одинаковых чётных степеней на сумму их оснований делится без остатка, что и требовалось доказать.

Итак, (x^2k - a^2k)/(x + a) = x^2k-1 - ax^2k-2 + … + a^2k-2x - a^2k-1.

3. Разность одинаковых нечётных натуральных степеней на сумму их оснований не делится .

Пусть P(x) = x^2k+1 - a^2k+1 - разность одинаковых нечётных степеней.

По теореме Безу при делении x^2k+1 - a^2k+1 на x + a = x - (-a) остаток равен

R = P(-a) = (-a)^2k+1 - a^2k+1 = -2a^2k+1 . Так как остаток при делении не равен 0, то разность одинаковых нечётных натуральных степеней на сумму их оснований не делится, что и требовалось доказать .

4. Сумма одинаковых нечётных натуральных степеней на сумму их оснований делится без остатка.

Пусть P(x) = x^2k+1 , P(-a) = (-a)^2k+1 = -а^2k+1 , тогда P(x) - P(-a) = x^2k+1 + a^2k+1 - сумма одинаковых нечётных натуральных степеней. По следствию 5

P(x) - P(-a) = x^2k+1 + a^2k+1= (x -(- a))Q(x)= (x + a)Q(x), а это значит, что

(x^2k+1 + a^2k+1)/(x + a) = Q(x), т.е. сумма одинаковых нечётных натуральных степеней на сумму их оснований делится без остатка.

Итак, (x^2k+1 + a^2k+1)/(x + a) = x^2k - ax^2k-1 + … - a^2k-1x + a^2k.

5. Сумма одинаковых чётных натуральных степеней на сумму их оснований не делится.

Пусть P(x) = x^2k + a^2k - сумма одинаковых чётных степеней.

По теореме Безу при делении x^2k + a^2k на x + a = x - (-a) остаток равен

R = P(-a) = (-a)^2k + a^2k = 2a^2k.

Т. к. остаток при делении не равен 0 , то сумма одинаковых чётных натуральных степеней на сумму их оснований не делится, что и требовалось доказать.

Пример. Сократить дроби:

а)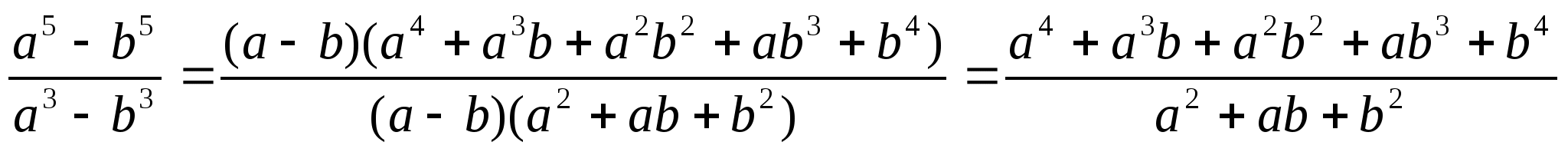

б)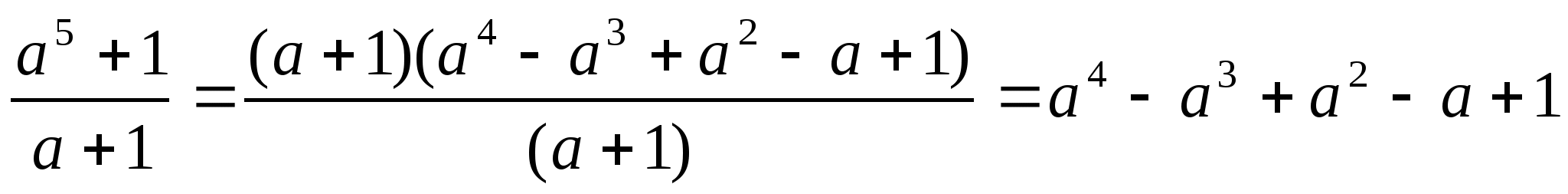

в)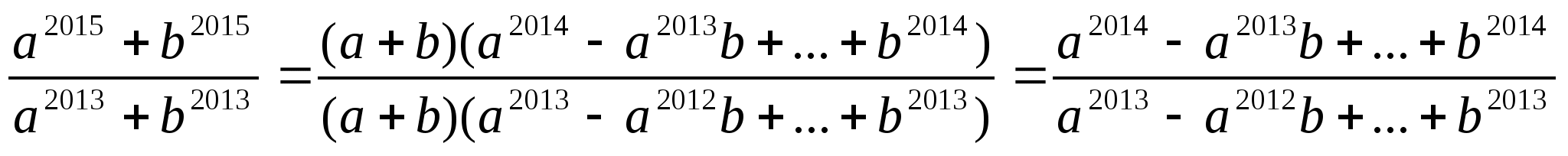

Пример. Доказать, что число 11¹⁰ - 1 делится на 100.

Решение.

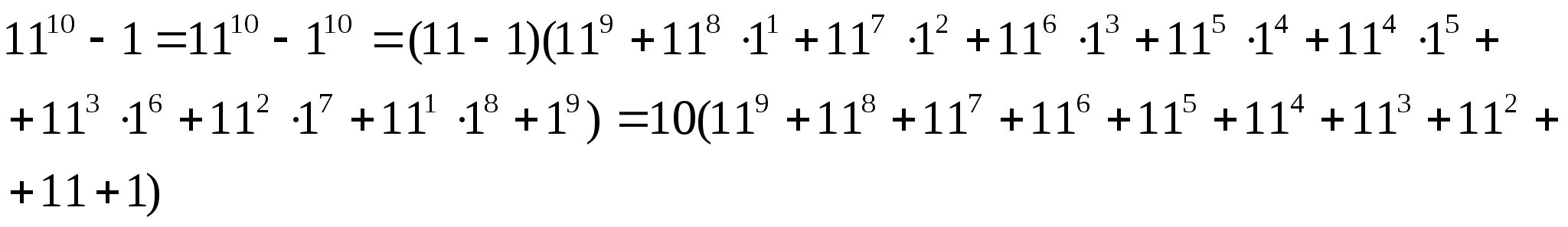В скобках все слагаемые заканчиваются единицей, их 10, значит, их сумма заканчивается нулем. Таким образом, второй множитель делится на 10, а все произведение делится на 100.

ЗАКЛЮЧЕНИЕ

В школе изучаются и используются так называемые формулы сокращенного умножения: квадраты и кубы суммы и разности двух выражений и формулы разложения на множители разности квадратов, суммы и разности кубов двух выражений. Обобщением этих формул является формула, называемая формулой бинома Ньютона и формулы разложения на множители суммы и разности степеней. Эти формулы часто используются в решении различных задач: на доказательство делимости, сокращение дробей, приближенные вычисления. Рассмотрены интересные свойства треугольника Паскаля, которые тесно связаны с биномом Ньютона.

В работе систематизирована информация по теме, приведены примеры задач на применение бинома Ньютона и формул суммы и разности степеней. Работа может быть использована в работе математического кружка, а также для самостоятельного изучения теми, кто увлекается математикой.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Виленкин Н.Я. Комбинаторика.- изд. "Наука". - М., 1969 г.

2. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций базовый и углубленный уровни - М.: Просвещение, 2014. - 431 с.

3. Решение задач по статистике, комбинаторике и теории вероятностей. 7-9 кл./ автор - составитель В.Н. Студенецкая. - изд. 2-е., испр., - Волгоград: Учитель, 2009 г.

4. Савушкина И.А., Хугаев К.Д., Тишкин С.Б. Алгебраические уравнения высших степеней /методическое пособие для слушателей межвузовского подготовительного отделения. - Санкт-Петербург, 2001.

5. Шарыгин И.Ф. Факультативный курс по математике: Решение задач. Учебное пособие для 10 кл. средней школы. - М.: Просвещение, 1989.

6. Наука и жизнь, Бином Ньютона и треугольник Паскаля [Электронный ресурс]. - Режим доступа: www.nkj.ru/archive/articles/13598/

ПРИЛОЖЕНИЯ

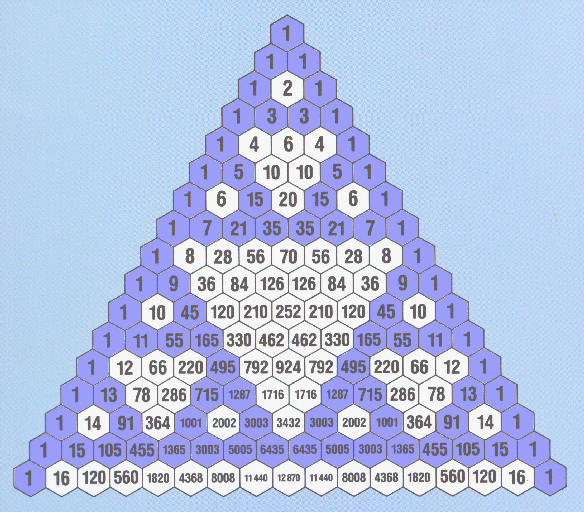
В треугольнике Паскаля выделены числа, которые делятся на 2.

.

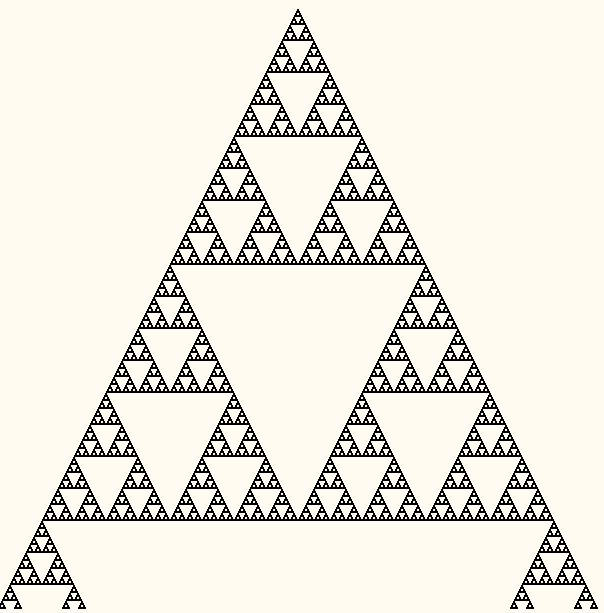
Получился известный фрактальный «треугольник Серпинского»

Треугольник, построенный "относительно" числа 7, то есть, числа, не делящиеся на 7 без остатка, нарисованы черным цветом, делящиеся - белым.

Красные треугольные "зоны Серпинского" накладываются на зеленые окна от девяток, и дают желтые зоны, а с синими участками от деления на 11 дают сиреневые участки.

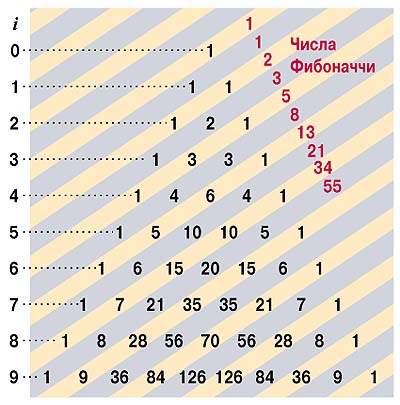
Числа Фибоначчи

Треугольник Паскаля, преобразованный по методу Пифагора: цифры числа суммируются до тех пор, пока не будет получено однозначное число (для любителей мистики)

Связь с простыми числами, обнаруженная в 1972 г. (Г.В. Манн и Д. Шенкс)

Кроме того, если номер строки - простое число, то все числа в строке, за исключением двух крайних единиц, делятся на номер строки.

kze.docdat.com/docs/264/index-30694.html</</u>