Программа элективного курса по геометрии Решение планиметрических задач (11 класс)

Программа элективного курса по геометрии

для учащихся 11 А класса 2016-17 учебный год.

Составила учитель математики МБОУ СОШ №4:

Перункова Галина Александровна.

Решение планиметрических задач.

Пояснительная записка.

Решение геометрических задач часто вызывает трудности у учащихся. Это в первую очередь связано с тем, что редкая задача в геометрии может быть решена с использованием определенной формулы. Большинство геометрических задач требуют применения разнообразных теоретических знаний, доказательства утверждений, справедливых лишь при определенном расположении фигуры, применение комплекса различных формул. Но и при хорошем знании теории приобрести навык в решении задач можно лишь решив достаточно много задач, начиная с простых и переходя к более сложным. Изменения в ЕГЭ по математике 2015г., действующие на сегодняшний день, касаются, прежде всего содержания КИМ-ов: увеличение количества геометрических задач, разделение задачи С4 на 2 вопроса. Поэтому очевидна актуальность введения элективного курса по геометрии. Курс рассчитан на 17 часов.

Цель курса:

• Закрепить и систематизировать теоретические и практические навыки при решении планиметрических задач;

• Научить выделять из общего количества задач ключевые задачи;

• Учить решать задачу несколькими способами и выбирать наиболее рациональный.

Задачи курса:

-сформировать целостное понятие геометрии;

-повысить мотивацию изучения геометрии;

-повысить качество знаний;

-повысить уровень образовательного процесса в целом

-подготовить учащихся к итоговой аттестации в форме ЕГЭ;

-научить решать сложные геометрические задачи;

- научить различным приемам решения задач, помогающим успешно справиться с заданиями при подготовке к ЕГЭ;

Содержание обучения

Изучение учебного материала курса строится поэтапно:

1 этап: повторение основных теоретических знаний. Содержание данного этапа указано для каждого раздела.

2 этап: решение простейших задач. Контроль работы учащихся в группах и парах. Работа по дидактическому материалу.

3 этап: решение трудных и нестандартных задач. Введение таких задач необходимо, так как решение одной сложной задачи может заменить решение нескольких простейших задач. Контроль работы учащихся на данном этапе осуществляется учителем.

4 этап: предварительный контроль в форме самостоятельной работы учащихся.

5 этап: решение задач по материалам ЕГЭ, составление справочного материала.

Повторение необходимых теоретических знаний представлено по следующим разделам:

Первый раздел «Построения на плоскости».

*алгоритм построения расстояния от точки до плоскости;

*метод вычислений длины искомого отрезка;

*замечательные свойства окружности (геометрические места точек);

*методы геометрических точек и прямых.

Второй раздел. «Треугольники и их элементы».

*виды треугольников (равносторонний, равнобедренный, прямоугольный);

* элементы треугольника и их свойства (медиана, биссектриса, высота, проекции катетов);

* теорема Пифагора;

* теорема косинусов;

* теорема синусов;

* средняя линия треугольника;

* подобие треугольников;

*теорема Менелая;

Третий раздел. «Окружность и ее элементы»

*различные случай касания окружностей;

*теорема о расстоянии от вершины треугольника до точки касания вневписанной окружности;

*теорема о пересекающихся хордах;

*теорема о длинах касательных, проведенных из одной точки к окружности;

*теорема о квадрате касательной;

*углы: между касательной и хордой; между двумя пересекающимися хордами; между двумя секущими; между касательной и секущей; между двумя касательными;

*углы, связанные с окружностью (центральные углы, вписанные углы);

Четвертый раздел. «Многоугольники».

*вписанные и описанные четырехугольники;

*теорема Птоломея;

* вписанные и описанные правильные многоугольники.

*теоремы о вписанных и описанных окружностях: для правильных, прямоугольных, произвольных треугольников, правильных и других четырехугольников.

Пятый раздел. « Векторы и метод координат»

Особенностью этого раздела является одновременное повторение данной темы по планиметрии и стереометрии.

*векторы, метод координат на плоскости;

Шестой раздел. «Метод площадей».

*формулы площади произвольных четырехугольников;

*формулы площади правильных многоугольников;

*отношение площадей подобных фигур.

*основные приемы нахождения площадей многоугольников;

*формула Пика.

Тематическое планирование элективного курса

Тема

Количество

часов

Построения на плоскости:

1-2. Метод геометрических точек, методы геометрических прямых,

метод вычислений (алгебраический метод)

Треугольник:

3. Замечательные точки и линии в треугольнике. Пропорциональные отрезки в треугольнике.

4-5. Вписанная в треугольник и описанная окружность.

Окружность и круг.

6.Свойство дуг и хорд.

7.Углы связанные с окружностью.

8. Средние геометрические и другие средние.

9. Теоремы Чевы и Менелая. Задачи на нахождение отрезков и площадей.

10. Решение нестандартных задач по теме: «Треугольник».

11. Метод подобия в задачах.

12. Решение задач по теме: «Подобие треугольников».

Окружности и касательные.

13. Взаимное расположение окружностей и общие касательные.

14. Вневписанные окружности.

Многоугольники.

15.Свойства правильных многоугольников.

16. Применение векторов к доказательству теорем и решению задач.

17. Метод площадей.

2

3

2

1

1

1

2

2

1

1

1

Итого:

17

Требования к уровню подготовки учащихся.

Планируемые результаты:

- овладение знаниями и умениями в области геометрии, необходимыми для изучения естественнонаучных дисциплин, продолжения образования и освоения избранной специальности на современном уровне;

-формирование навыков обобщения и систематизации теоретических знаний для решения задач;

-развитие логического мышления, алгоритмической культуры, математического мышления и интуиции, необходимых для успешной адаптации к реальной жизни и выбора профессии;

- формирование навыков исследовательской деятельности, постановки и решения проблемных вопросов; умение сравнивать, анализировать, рассуждать, выдвигать гипотезы, доказывать, делать выводы, творчески подходить к любому делу;

- формирование навыков самообразования, критического мышления, самоорганизации и самоконтроля, работы в команде.

Система оценки достижений учащихся: В технологии проведения занятий присутствует элемент самопроверки, взаимопроверки, который предоставляет учащимся возможность самим проверить, как ими усвоен изученный материал. Результаты тестирования проверяются с помощью современных технологий. Самостоятельные, контрольные, зачетные работы проверяются учителем. Для каждого ученика заполняется индивидуальный лист контроля.

Литература:

1. И.Ф.Шарыгин «Факультативный курс по математике».

2. Т.Дорофеев, М.Попов «Математика для поступающих в вузы»

3. Л.С. Атанасян В.Ф. Бутузов «Дополнительные главы к школьному учебнику»

4. О.Ю. Черкасов, А.Г.Якушев «Математики»

5. А.А.Прокофьев «Геометрия для поступающих в втузы».

Образовательные диски.

1.Стереометрия. Авторы курса - Р.П.Ушаков и С.А.Беляев.

2.Учебная программа «Математика абитуриенту. Версия 2.0». Автор В.В.Ткачук. Разделы планиметрия и стереометрия.

3.Математика. Раздел геометрия. Автор Синицын А.И. 2008.

Примерная разработка занятия 9.

Цели: повторить теоретические знания по теме треугольники и их элементы, применить знания при решении нестандартных задач.

Ход занятия.

1. Повторение основных теоретических знаний в парах.

2. Лекция, составление опорного конспекта по следующему теоретическому материалу.

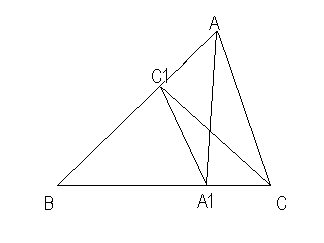
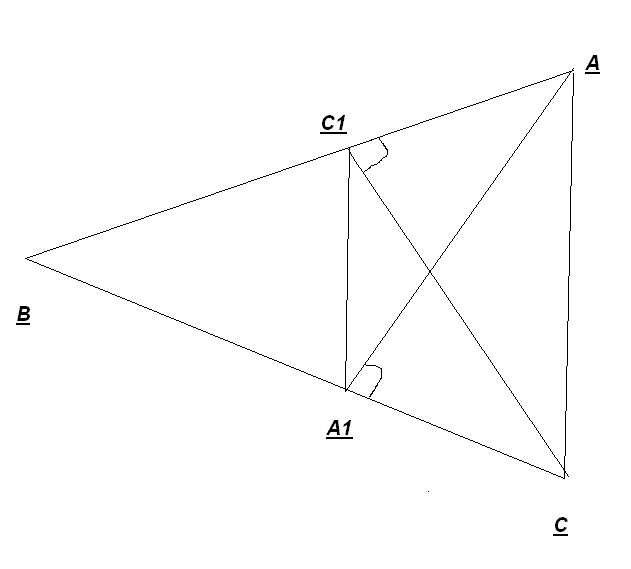
Теорема. Пусть в остроугольном треугольнике ABC проведены высоты AA₁ и CC₁.

Тогда Δ A₁BC₁ и ΔABC подобны, причём коэффициент подобия равен Cos<B.

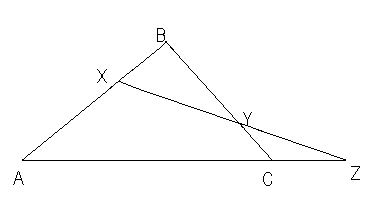
Теорема (теорема Менелая). Если некоторая прямая пересекает стороны АВ и ВС треугольника АВС в точках Х и У соответственно, а продолжение стороны АС- в точке Z, то AX/XB∙BY/YC∙CZ/ZA=1

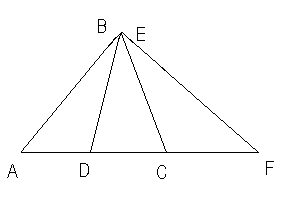
Лемма1. Если стороны АС и DF треугольников ABC и DEF лежат на одной прямой или на параллельных прямых, то S_ΔABC/S_ΔDEF=AC/DF

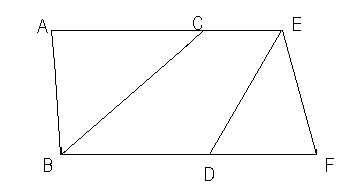
Лемма 2. Если два треугольника имеют общую сторону АС, то S_ΔABC/ S_ΔAB1C= BD/B₁D

Лемма 3. Если треугольники АВС и АВС₁ имеют общий угол А, то

3. Комментированное решение следующих нестандартных задач.

Задачи, взятые из контрольно-измерительных материалов единого государственного экзамена (после смены концепции ЕГЭ). Коллективного решение одной задачи необходима комбинировать с самостоятельной работой по воспроизведению решения нестандартных задач.

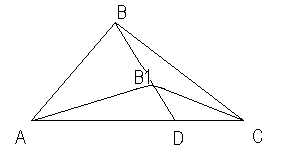
Задача №1

В треугольнике АВС на стороне АВ взята точка К так, что АК: КВ= 1:2, а на стороне ВС взята точка L так, что С L: LВ= 2:1. Пусть Q- точка пересечения прямых АL и СК. Найдите площадь треугольника АВС, зная, что площадь треугольника ВQС равна 1.

Решение

Пусть АК=Х , тогда КВ=2Х. Пусть ВL=у, тогда LС=2у.

Применим теорему Менелая к треугольнику АВL и секущей КQ и получим:

ВК/КА*АQ/QL*LС/ВС=1

2х/х* АQ/QL*2у/3у=1

АQ/QL=3/4

АQ= 3 части, QL= 4 части, тогда АL/QL=7/4

По лемме 2:

S⌂_ABC/S⌂QBC=AL/QL=7/4, т.к ⌂АВС и ⌂QBC имеют общую сторону BC

Итак, S⌂АВС/ S ⌂QBC=7/4, но S ⌂QBC=1, тогда S⌂АВС=7/4

Ответ: 7/4

Задача № 2

В трапеции АВСД диагональ АС перпендикулярна боковой стороне СД, а диагональ ДВ перпендикулярна боковой стороне АВ. Продолжения боковых сторон АВ и ДС пересекаются в точке К, образуя треугольник АКД с углом 45 градусов при вершине К. Площадь трапеции АВСД равна S. Найти площадь треугольника АКД

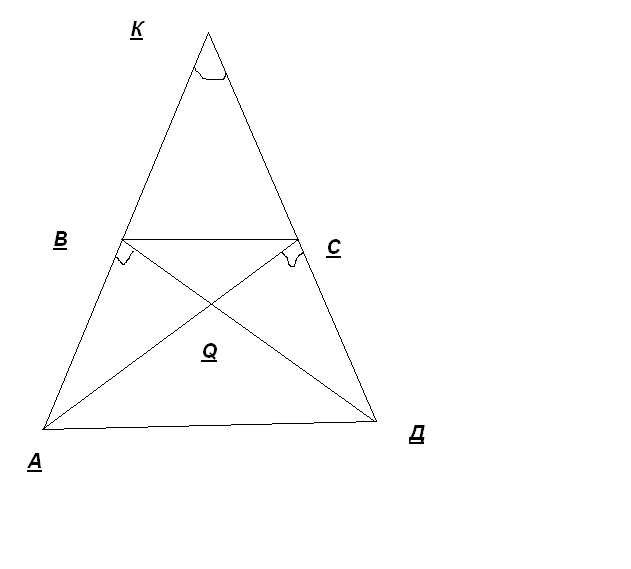
Решение.

Теорема: Пусть в остроугольном треугольнике АВС проведены высоты АА₁ и СС_{1 .} Тогда треугольники А₁ВС₁ и треугольник АВС подобны, причём коэффициент подобия равен cos<В

⌂КВС подобен ⌂КАД по предыдущей теореме и k= cos45⁰=√2/2, следовательно,

S⌂_КАД/S⌂_КВС==(√2/2)² = ½, а это значит площадь ⌂КВС равна половине площади ⌂КАД, но S_{трапеции}= S , S⌂_КВС= S, тогда

S⌂_КАД=2S.

Ответ: 2S

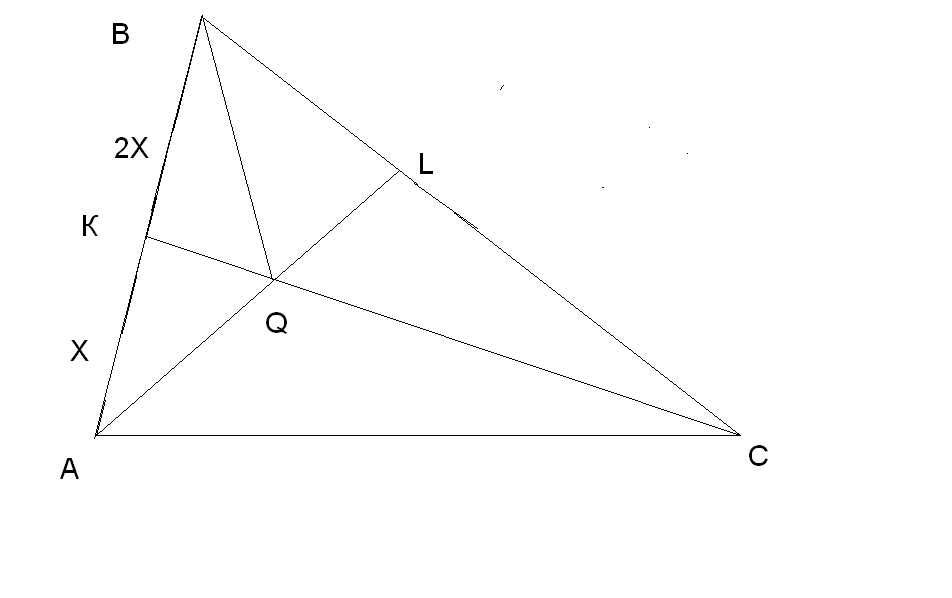
Задача №3

Точки Р и Q расположены на стороне ВС ∆АВС так, что ВР/РQ/ QС=1/2/3.Точка R делит сторону АС этого треугольника таким образом, что АR/RС=1/2.Чему равно отношение площади четырёхугольника РQST к площади ∆АВС, где S и T - точки пересечения прямой ВRС прямыми АQ и АР соответственно.

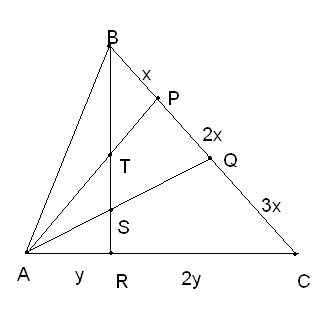
Решение:

Пусть ВР=х, АR=у, тогда РQ=2х,QC=3x, RC=2у.

Применим теорему Менелая к ∆АСQ и секущей SR и получим

СR/AR * AS/SQ * BQ/BC = 1; 2y/y * AS/SQ * 3x/6x = 1; AS/SQ = 1;

AS= 1 часть, SQ= 1 часть; AS/AQ = 1/2.

Применим теорему Менелая к ∆АСР и секущей ТR получим:

СR/AR *АТ/ТР * ВР/ВС = 1; 2y/y * АТ/ТР * x/6x = 1; АТ/ТR = 3;

АТ = 3 части, ТR = 1 часть,

Тогда АТ/АР = 3/4.

К ∆AST и ∆АРQ применим лемму: если треугольники AST и АРQ имеют общий угол, то S_∆AST/S_∆АРQ = АТ*AS/AP*AQ = 3/4 * 1/2 = 3/8

S_∆AST = 3 части, S_{∆АРQ =} 8 частей, тогда S_TSQP= 5 частей,

Значит, S_PQTS/ S_∆АРQ = 5/8.

У ∆АВС и ∆АРQ основания ВС и РQ лежат на одной прямой, тогда применим лемму: если стороны ВС и РQ лежат на одной прямой (или на параллельных прямых), то

S_∆АРQ/ S_∆АВС = РQ/ ВС = 2х/6х = 1/3;

тогда S_∆АРQ= 1 часть, S_∆АВС = 3 части.

S_{∆АРQ =} 1/3 _*S_{∆АВС = 8;}

S_{∆АВС =} 24

S_PQST/ S_∆АРQ = 5/24.

Ответ:5/24.

Задача для самостоятельного решения или Д/з: Площадь треугольника АВС равна 28, точка К делит сторону АВ в отношении ВК:КА=3:1, а точка Е - сторону ВС в отношении СЕ:ЕВ=1:3. Прямые СК и АЕ пересекаются в точке М. Найдите площади треугольника АКМ и четырёхугольника КВЕМ.