Конспект урока по теме: Рациональные числа (6 класс)

Тема: Умно­же­ние и де­ле­ние по­ло­жи­тель­ных и от­ри­ца­тель­ных чисел

Урок: Ра­ци­о­наль­ные числа.

Продолжительность: 1 урок (40 мин).

Класс: 6.

Цели урока:

Образовательные:

- введение понятия рациональных чисел, запись рациональных чисел либо в виде десятичной дроби, либо в виде периодической дроби.

Развивающие:

- развитие речи, мышления;

- совершенствование умственной деятельности: анализ, способность наблюдать, делать выводы, составлять алгоритм решения, проверять результаты.

Воспитательные:

- воспитание информационной культуры, поддержание интереса к математике, через расширение знаний учащихся об истории математики.

Тип урока: объяснение нового материала.

1. Организационный момент. Мотивация к учебной деятельности.

Приветствие. Проверка готовности к уроку.

- Здравствуйте, ребята! Садитесь! Я очень рада видеть вас на своем уроке! Желаю Вам сегодня хорошо поработать на уроке! А девиз нашего урока будет таким:

Математика, друзья!

Абсолютно всем нужна.

На уроке работай старательно

И успех тебя ждет обязательно!

- Вы со мной согласны?

2. Практическая деятельность учащихся.

Анализ самостоятельной работы, разбор примеров, в которых часто встречались ошибки.

3. Подготовка к работе на основном этапе.

Рас­смот­рим за­пи­сан­ные числа.

Сна­ча­ла за­пи­са­ны при­ме­ры целых чисел. 2 - это целое по­ло­жи­тель­ное число. -3- это целое от­ри­ца­тель­ное число. Число ноль - целое число, ко­то­рое не яв­ля­ет­ся ни по­ло­жи­тель­ным, ни от­ри­ца­тель­ным.

Далее за­пи­са­ны при­ме­ры по­ло­жи­тель­ных и от­ри­ца­тель­ных дроб­ных чисел, а затем при­ме­ры сме­шан­ных чисел.

По­про­бу­ем все эти числа за­пи­сать в виде от­но­ше­ния:

Любое целое число можно за­пи­сать в виде такой обык­но­вен­ной дроби, взяв за зна­ме­на­тель еди­ни­цу, а за чис­ли­тель - само это число.

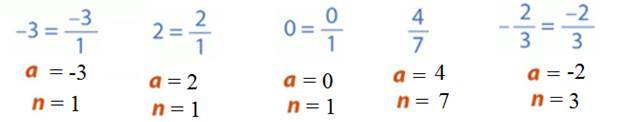
Рас­смот­рим обык­но­вен­ные дроби. Число уже пред­став­ля­ет собой ис­ко­мую дробь.

Дробь можно за­пи­сать как . От­ме­тим удоб­ный тех­ни­че­ский прием. Знак минус, ко­то­рый стоит перед дро­бью, можно при необ­хо­ди­мо­сти за­пи­сать или в чис­ли­тель, или в зна­ме­на­тель.

Пред­ста­вим рас­смат­ри­ва­е­мые де­ся­тич­ные дроби как обык­но­вен­ные.

Итак, любую де­ся­тич­ную дробь можно за­пи­сать в по­доб­ном виде. Для этого нужно:

Любое сме­шан­ное число можно пред­ста­вить в виде непра­виль­ной дроби.

Итак, мы смог­ли за­пи­сать все дан­ные числа в виде от­но­ше­ния . Более того, мы по­ня­ли, как найти для лю­бо­го из­вест­но­го нам числа. Зна­чит, мы по­лу­чи­ли при­знак, ко­то­рый объ­еди­ня­ет их в одно мно­же­ство. Это мно­же­ство на­зы­ва­ет­ся мно­же­ством ра­ци­о­наль­ных чисел. Сфор­му­ли­ру­ем опре­де­ле­ние.

Это интересно. Название «рациональные числа» происходит от латинского слова «рацион», что значит «отношение, деление».

6. Усвоение новых знаний и способов действий.

6.1. с. 204, №1178

- Какие числа называются рациональными?

6.2. с. 204, №1179

- Что надо сделать, чтобы суммы представить в виде а/n?

(Найти значение каждой сумы.)

6.3. Работа по цепочке.

- Приведите примеры рациональных чисел. Докажите это.

7. Включение в систему знаний и повторение.

с. 26 №1190

8. Самостоятельная работа и осуществление контроля:

Вариант 1.

Покажите, что числа являются рациональными:

0,85; -3,4; -1 3/8; 5 5/6; 12

Вариант 2.

Покажите, что числа являются рациональными:

0,63; -2,7; -4 4/9; 6 3/7; 14

9. Рефлексия учебной деятельности и оценивание учащихся.

- Какие числа называются рациональными?

- Как доказать, что любое число является рациональным?

- Что вам показалось трудным при изучении новой темы?

- Что самым легким?

10. Домашнее задание: п. 37 №1196, 1200

6. Перевод обыкновенных дробей в десятичные

Рас­смот­рим при­ме­ры.

Пе­ре­ве­дем обык­но­вен­ную дробь в де­ся­тич­ную. Дроб­ную черту можно за­ме­нить зна­ком де­ле­ния. Зна­чит, . Вы­пол­нив де­ле­ние в стол­бик, по­лу­чим 0,4. За­ме­тим, что это можно было сде­лать иначе. Число 10 крат­но 5. По­это­му дробь можно при­ве­сти к зна­ме­на­те­лю 10, умно­жив ее чис­ли­тель и зна­ме­на­тель на 2.

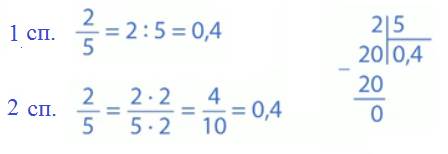
По­про­бу­ем, рас­суж­дая ана­ло­гич­но, пе­ре­ве­сти обык­но­вен­ную дробь в де­ся­тич­ную. Будем де­лить 1 на 3 в стол­бик. По­лу­чим сна­ча­ла ноль целых, потом 3 де­ся­тых. Далее при де­ле­нии все время будут по­вто­рять­ся оста­ток 1, а в част­ном - цифра 3. Де­ле­ние ни­ко­гда не кон­чит­ся. Эту дробь нель­зя пред­ста­вить в виде де­ся­тич­ной дроби. Для за­пи­си числа нужна бес­ко­неч­ная де­ся­тич­ная дробь.

Сде­ла­ем вывод.

На­при­мер, дроби можно пе­ре­ве­сти в де­ся­тич­ную дробь, а вот дробь пе­ре­ве­сти нель­зя.

7. Периодические дроби

Рас­смот­рим дробь . Раз­де­лим 5 на 11. По­лу­чим в част­ном 0 целых, 4 де­ся­тых, 5 сотых. Далее при де­ле­нии все время будут че­ре­до­вать­ся оста­ток 5 и 6, а в част­ном - цифры 4 и 5. Такую за­пись на­зы­ва­ют пе­ри­о­ди­че­ской дро­бью.

Сде­ла­ем за­ме­ча­ние.

Любое ра­ци­о­наль­ное число можно за­пи­сать не толь­ко в виде обык­но­вен­ной дроби, но и в виде либо де­ся­тич­ной, либо пе­ри­о­ди­че­ской дроби.

Рас­смот­рим, как за­пи­сы­ва­ют и чи­та­ют пе­ри­о­ди­че­ские дроби:

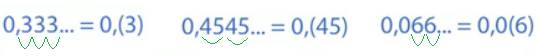
8. Заключение</</p>

Мы видим, что в этих за­пи­сях одна или несколь­ко цифр по­вто­ря­ют­ся бес­ко­неч­но много раз. По­вто­ря­ю­щу­ю­ся часть на­зы­ва­ют пе­ри­о­дом дроби. Дан­ные числа можно про­честь так: ноль целых и три в пе­ри­о­де; ноль целых и сорок пять в пе­ри­о­де; ноль целых, ноль де­ся­тых и шесть в пе­ри­о­де.