- Учителю
- «Работа с одаренными детьми как важнейшие требования деятельности учителя» (задания для проведения непрерывной олимпиаде по математике 5-6 классы, школьные олимпиадные задания по математики 5-11 классов, развивающий материал для закрепления математики 5-6
«Работа с одаренными детьми как важнейшие требования деятельности учителя» (задания для проведения непрерывной олимпиаде по математике 5-6 классы, школьные олимпиадные задания по математики 5-11 классов, развивающий материал для закрепления математики 5-6
ГУ «Ярославская средняя школа отдела образования Есильского района»

«Работа с одаренными детьми как важнейшие требования деятельности учителя»
(задания для проведения непрерывной олимпиаде по математике 5-6 классы, школьные олимпиадные задания по математики 5-11 классов, развивающий материал для закрепления математики 5-6 классы).
Методическое пособие для учителя

2014 год
От автора
«Одаренными называют тех, которые по оценке опытных специалистов, в силу выдающихся способностей демонстрируют высокие достижения в одной или нескольких сферах: интеллектуальной академических достижений, творческого или продуктивного мышления, общения или лидерства, художественной деятельности, двигательной сфере».
Целью обучения математики в школе является не только овладение конкретными математическими знаниями, но и интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для продуктивной жизни в обществе. В настоящий момент образование характеризуется как процесс обучения и воспитания в интересах личности, общества и государства, направленный на развитие индивида, его индивидуальных, умственных и физических способностей, одаренности и таланта.
Анализ учебников математики для 5-6 классов показывает, что не один из учебников не содержит необходимого набора задач, направленных на развитие одаренных учащихся, т.е. задач на развитие различных познавательных процессов, обеспечивающих достижение целей развития способных детей. Современные образовательные стандарты, программы математического образования для общеобразовательной школы лишь отмечают развивающие возможности математики, но не уделяют внимания их использованию для развития одаренных детей в процессе обучения.
Цель работы:
изучить особенности развития одарённых детей в процессе обучения математике и подготовить на этой основе конкретные методические разработки.
Задачи:
-
- раскрыть сущность понятия «одаренность»;
-
выявить основные способы диагностики одаренности;
-
изучить взгляды педагогов на выявление-развитие детской одаренности;
-
- проанализировать учебно-методическое обеспечение процесса обучения математике с точки зрения выявления его потенциала для развития одарённых учащихся;
-
построить систему задач по конкретной теме курса математики, направленную на развитие одаренных детей;
-
определить место использования таких задач в учебном процессе.
-
беседы, анкетирование учителей и родителей учащихся средней школы;
-
наблюдение за процессом обучения в средней общеобразовательной школе.
Как же определить у ребенка наличие математических способностей?
1. Быстрое овладение математическими знаниями, умениями и навыками. Быстрота понимания объяснения учителя.
2. Логичность, самостоятельность мышления.
3. Находчивость и сообразительность при изучении математики.
4. Быстрое и прочное запоминание материала.
5. Высокая степень развития способности к обобщению, анализу и синтезу математического материала.
6. Пониженная утомляемость при занятиях математикой.
7.Способность быстро переключаться с прямого на обратный ход мысли.
Основные способы работы учителей с одаренными детьми:
-
факультативы
-
кружки
-
подготовка к олимпиадам
-
проведение конкурсов
Возможность реализации целей развития одарённых детей во внеклассной работе
-
Помимо возможности развития одаренных учащихся на уроках математики, есть возможность реализации целей развития способных детей и во внеучебное время, во внеклассной работе. Основной формой внеклассной работы во время учебного года являются кружковые занятия.
-
Одна из основных функций кружковых и факультативных занятий - это подготовка способных учащихся к участию в олимпиадах.
-
Моей работой с одаренными детьми является проведения кружка по математике «Занимательная математика».
-
Целью кружковой работы является не только овладение учащимися умениями и навыками, но развитие в детях математических способностей, различных качества ума, вычислительной культуры, элементов творческой деятельности, научного мировоззрения.
-
На кружок дети ходят с удовольствием. В работе я использую различные методы, такие как игровой, групповой, проблемно-поисковый и метод самостоятельной работы учащихся.
-
Так же работой с одаренными детьми является участие в конкурсе «Кенгуру».
-
Проведение олимпиад на школьном уровне.
-
Подготовка детей к олимпиадам районного уровня (внедрение заданий олимпиадного характера во внеклассную работу).
Помощь одаренным учащимся в самореализации их творческой направленности
-
Ø Создание для ученика ситуации успеха и уверенности, через индивидуальное обучение и воспитание;
-
Ø организация научно-исследовательской деятельности;
-
Ø организация и участие в интеллектуальных играх, творческих конкурсах, предметных олимпиадах, научно-практических конференциях.
-
Ø разработка и реализация межпредметных научно-исследовательских проектов.
-
Ø изготовление компьютерных презентаций, видеороликов, исследований.
Поощрение одаренных детей
-
Ø Публикация в СМИ, на сайте школы;
-
Ø Награждение.
Рекомендации учителям:
-
Учителю не следует уделять слишком много внимания
игровому обучению с ярко выраженным элементом соревнования. Одаренный ребенок будет чаще
всего оказываться победителем, что может вызвать
неприязнь соучеников и не благоприятствует созданию атмосферы всеобщей заинтересованности, к которой
стремится учитель.
-
Учитель не должен возводить одаренного ребенка на
пьедестал или делать из него вундеркинда в глазах других учеников. Успехи его будут должным образом оценены, а неуместное выпячивание его исключительности достижений рождает чаще всего раздражение, ревность и отторжение вместо ожидаемой похвалы. Другая крайность - преднамеренное публичное принижение уникальных способностей и даже сарказм со стороны учителя,- конечно, недопустима.
-
Не занимайтесь наставлениями, помогайте детям действовать независимо, не давайте прямых инструкций относительно того, чем они должны заниматься.
-
Не сдерживайте инициативы и не делайте за них то, что они могут сделать самостоятельно.
-
Научите школьников прослеживать межпредметные связи и использовать знания, полученные при изучении других предметов.
-
Приучайте детей к навыкам самостоятельного решения проблем, исследования и анализа ситуации.
-
Используйте трудные ситуации, возникшие в школе или дома, как область приложения полученных навыков при решении задач.
-
Помогайте детям научиться управлять процессом усвоения знаний.
Представляю брошюру «Работа с одаренными детьми как важнейшие требования деятельности учителя», разработанную на основе Программы 7 модулей третьего базового уровня.
Брошюра «Работа с одаренными детьми как важнейшие требования деятельности учителя» включает в себя следующие разделы:
-
Задачи на развитие логического мышления.
-
Занимательные вопросы.
-
Задачи в стихах.
-
Непрерывные олимпиады по математике 5-6 классов.
-
Олимпиадные задания по математике 5-11 классов.
-
Раскраски.
Спасибо за внимание!
Желаю успехов!
Раздел 1.Задачи на развитие логического мышления.
-
Жили-были две фигуры: Круг и Квадрат. На их улице было 3 дома: один дом был с окном и трубой, другой с окном, но без трубы, третий с трубой, но без окна. Каждая фигура жила в своем доме. Круг и квадрат жили в домах с окнами. Квадрат любил тепло и часто топил печку. Кто в каком доме жил?
-
Тремя линиями отделить деревья от зайцев.

-
Переложить 1 палочку так, чтобы домик был перевернут в другую сторону.

Раздел 2.Занимательные вопросы.
-
Сколько ушей у трёх мышей?
-
Сколько лап у двух медвежат?
-
У семи братьев по одной сестре. Сколько всего сестёр?
-
У бабушки Даши внучка Маша, кот Пушок и собака Дружок. Сколько всего внуков у бабушки?
-
Над рекой летели птицы: голубь, щука, 2 синицы, 2 стрижа и 5 угрей. Сколько птиц? Ответь скорей!
-
Горело 7 свечей. 2 свечи погасили, а остальные продолжали гореть. Сколько свечей осталось? (2, остальные сгорели).
-
В корзине три яблока. Как поделить их между тремя детьми так, чтобы одно яблоко осталось в корзине? (Отдать одно яблоко вместе с корзиной).
-
На берёзе три толстых ветки, на каждой толстой ветке по три тоненьких веточки. На каждой тоненькой веточке по одному яблочку. Сколько всего яблок? (Нисколько - на берёзе яблоки не растут.)
Раздел 3.Задачки - шутки.
-
На столе три стакана с ягодами. Вова съел один стакан ягод. Сколько стаканов осталось на столе? (Три)
-
Шли двое, остановились, один у другого спрашивает: «Это черная?». - «Нет, это красная». - «А почему она белая?» - «Потому, что зеленая». О чем они вели разговор? (О смородине)
-
На столе лежат два апельсина и четыре банана. Сколько овощей на столе? (Нисколько)
-
На груше росло десять груш, а на иве на две груши меньше. Сколько груш росло на иве? (Нисколько)
-
На какое дерево сядет воробей после дождя? (На мокрое)
-
Чего больше в квартире: стульев или мебели? (Мебели)
-
Ты да я да мы с тобой. Сколько нас всего? (Два)
-
Как можно сорвать ветку, не спугнув на ней птичку? (Нельзя, улетит).
Занимательная математика для учащихся 5-7 классов.
-
Задача - шутка:
Длина каждой палочки 6 сантиметров. Как из 13 таких палочек сложить метр? Палочки можно заменить спичками.
-
Волшебный квадрат:
4
5
1
Даны числа: 1,2,3,4,5,6,7,8,9. часть из них расставлена по клеткам. Расставьте остальные так, чтобы в любом направлении в сумме получалось 15.
-
Разные интересные задачи:
-
Сколько потребуется цифр для нумерации 32-х страниц книги, начиная с первой?
-
Что больше: сумма всех цифр или их произведение?
-
Назовите 4 последние цифры произведения целых чисел от 1 до 20?
-
Произведение трех последовательных нечетных чисел равно 105. найдите эти числа
-
Развлечения. Игры. Для учащихся 5-7 классов.
-
НЕ ОТРЫВАЯ КАРАНДАША ОТ БУМАГИ и не проходя ни один отрезков дважды, изобразите фигуру, как на
рисунке.
-
СКОЛЬКО БРАТЬЕВ И СКОЛЬКО СЕСТЕР?
Вы можете узнать, сколько братьев и сестер у вашего товарища. Пусть он прибавит к числу братьев 3, полученное число умножить на 5, к полученному произведению прибавит 20, сумму умножить на 2, прибавить число сестер и еще 5. по названному результату этих вычислений вы можете легко установить, сколько братьев и сестер у вашего товарища. Как вам это сделать?
-
ДЕЛИМОСТЬ НА 11.
Предложите товарищу написать на классной доске или бумаге, любое многозначное число. К этому числу вы можете быстро приписать справа или слева одну цифру так, чтобы получившееся число разделилось на 11. если например, ваш товарищ напишет число 43572, то вам нужно будет приписать справа или слева к этому числу 1. получившееся число разделить на 11.
Знаете ли вы, какую цифру нужно к числу, чтобы разобраться в этом вопросе, воспользуйтесь признаком делимости на 11: на 11 делятся те и только те числа, у которых сумма цифр, стоящих на нечетных местах, либо равна сумме цифр, занимающих четные места, либо больше или меньше ее на число, делящееся на 11.
Раздел 4.Задачи в стихах.
Решила старушка ватрушки испечь.
Поставила тесто да печь затопила.
Решила старушка ватрушки испечь,
А сколько их надо - совсем позабыла.
Две штучки - для внучки,
Две штучки - для деда,
Две штучки - для Тани,
Дочурки соседа... Считала, считала, да сбилась,
А печь-то совсем протопилась!
Помоги старушке сосчитать ватрушки. В. Кудрявцева
Раздел 5. Непрерывные олимпиады по математике 5-6 классов.
5 класс
Сентябрь
-
У Ани и Тани вместе 10 конфет, но у Тани на 2 конфеты больше, чем у Ани. Сколько конфет у Тани?
-
Имеются песочные часы на 3 минуты и 7 минут. Надо опустить яйцо в кипящую воду ровно на 4 минуты. Как это сделать с помощью данных песочных часов?
-
От старта до финиша на одинаковых расстояниях один от одного поставили флажки. Спортсмен пробегает расстояние от 1- го флажка до 8- го флажка за 7 секунд. За какое время он добежит до 12- го флажка?
-
На школьной викторине было предложено 20 вопросов. За каждый правильный ответ участнику начисляли 12 баллов, а за каждый ошибочный ответ - списывали 10 баллов. Сколько правильных ответов было у участника, если он ответил на все вопросы и набрал 86 баллов?
-
Три девочки одеты в белую, красную и синюю юбки. Туфли у них этого же цвета. Только у Нины юбка и туфли одного цвета, у Веры туфли красные, а у Ани туфли не белые. Определите цвет юбки и туфель у каждой из девочек.
-
В записи 8 8 8 8 8 8 8 8 поставьте между некоторыми цифрами знак сложения так, чтобы сумма равнялась тысяче.
-
У скольких пятизначных чисел сумма цифр равна 3?
-
Из числа 180032678910 вычеркните 6 цифр так, чтобы полученное число было наибольшим из возможных чисел.
-
Сколько потребуется цифр для нумерации 255 страниц книги?
-
Восстановите числа: 6**7
- 1345
*63*
Октябрь
-
У мальчика столько сестер, сколько братьев, а у его сестры вдвое меньше сестер, чем братьев. Сколько в этой семье братьев и сколько сестер?
-
В ящике имеется 3 черных и 5 белых шаров. Какое наименьшее число шаров нужно взять из ящика(не заглядывая в него), чтобы среди вынутых шаров оказался хотя бы один белый?
-
Разрежьте фигуру, изображенную на рисунке, на 4 равные части. (Разрезать можно только по сторонам и диагоналям клеточек.)
-
Поросята Ниф-Ниф и Нуф - Нуф бежали от Волка к домику Наф- Нафа. Волку бежать до поросят (если бы они стояли на месте) 4 минуты. Поросятам бежать до домика Наф - Нафа 6 минут. Волк бежит в 2 раза быстрее поросят. Успеют ли поросята добежать до домика Наф- Нафа?
-
Как с помощью пятилитровой кастрюли и трехлитровой банки налить из водопроводного крана в ведро ровно 4 л воды?
-
Алеша задумал число. Он прибавил к нему 5, потом разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число задумал Алеша?
-
Написано 99 чисел: 1, 2, 3, …., 98, 99. Сколько раз в записи встречается число 5?
-
На какое наибольшее число различных частей могут разбивать плоскость три окружности?
-
Отцу и сыну вместе 65 лет. Сын родился, когда отцу было 25 лет. Какого возраста отец и сын?
-
Маленький Мук и королевский скороход соревновались в беге по дорожке длиной 30 км, которая шла вокруг большого луга. По условиям соревнования, выигрывает тот, кто обгонит другого, пробежав на круг больше. Скороход делает круг за 10 минут, а Маленький Мук - за 6 минут. Оба бегут равномерно. Через сколько минут Маленький Мук обгонит скорохода?
Ноябрь
-
Группа туристов состоит из 6 иностранцев. Они говорят только по-французски или по-английски. 3 человека говорят только по-английски, 2 человека только по-французски. Сколько человек говорят на двух языках: и по-французски и по-английски?
-
Запиши число 100 девятью разными цифрами, соединенными знаками действий.
-
Три товарища - Алимбек, Коля и Султан - сели на скамейку в один ряд. Сколько способами они могут это сделать?
-
В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежат яблоки какого - то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?
-
Мать поручила детям - брату и сестре - разложить пакеты конфет так, чтобы на завтра к обеду для гостей было оставлено половина всех конфет и еще 3 штуки; к завтраку для всей своей семьи - половина оставшихся конфет и еще 3 штуки и к вечернему чаю - половина оставшихся конфет и еще 3 штуки. Дети разложили конфеты в три вазы так, как велела им мать, и у них осталось еще 4 конфеты, которые им разрешили съесть самим. Сколько всего конфет было в пакете?
-
Поезд длиной 20 м проезжает мимо километрового столба за 10 секунд. Сколько ему потребуется времени, чтобы проехать мост длиной 40 м?
-
Сколькими нулями заканчивается произведение всех натуральных чисел от 1 до 25 включительно?
-
Произведение трех чисел последовательных натуральных чисел равно 504. Найдите эти числа.
-
Замените каждую * (звездочку)цифрой так, чтобы получились верные равенства.
*****
Х ___72
20*82
+7273*
***15*
10.Большая стирка. После семи часов стирки длина, ширина и высота куска мыла уменьшилась вдвое. На сколько часов стирки еще хватит мыла?
Декабрь
-
Четно или нечетно число 1+2+3+…+2002+2003?
-
Летели галки, сели на палки. Сядут по одной - галка лишняя, сядут по две - палка лишняя. Сколько было галок? Сколько было палок?
-
3 курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 12 кур за 12 дней, если они будут нести такое же и одинаковое количество яиц за один и тот же промежуток времени?
-
В классе 35 учеников. Можно ли утверждать, что среди них найдутся хотя бы два ученика, фамилии которых начинаются с одной и той же буквы?
-
Капитан Врунгель погнался за кенгуру, в сумку которого попал мячик для гольфа (спортивная игра в мяч). Кенгуру в минуту делает 70 прыжков, каждый прыжок - 10 м. капитан Врунгель бежит со скоростью 10 м/с. Догонит ли он кенгуру?
-
Илья Муромец, Добрыня Никитич, Алеша Попович вступили в бой с несколькими великанами. Каждый великан получил по 3 удара богатырскими палицами, в результате чего все великаны обратились в бегство. Больше всего ударов нанес Илья Муромец - 7, меньше всего Алеша Попович - 3. Сколько всего было великанов?
-
На какое число надо разделить 87912, чтобы получилось тоже пятизначное число, записанное теми же цифрами, но в обратном порядке?
-
Моторчик пропеллера Карлсона работает на смеси томатного, тыквенного и ананасового сока. Процедура «заправки» соком следующая: Карлсон берет полный стакан томатного сока (200 мл) и делает из него четыре глотка, выливает в стакан полный пакет (150 мл) ананасового сока и делает три глотка и, наконец, выливает в стакан пакет (55 мл) тыквенного сока и в два глотка допивает смесь. Сколько сока Карлсон выпивал за один глоток, если все его глотки были одинаковы?
-
К данному трехзначному числу дважды приписывают точно такое же число, и полученное число делят на данное. Каким будет частное?
-
Восстановите числа: 14** *7
- **5 **
-**
*1
0
Январь
-
Мотоциклист ехал в поселок. По дороге он встретил три легковые машины и грузовик. Сколько всего транспортных средств шло в этот поселок?
-
Четыре человека обменялись рукопожатиями. Сколько было рукопожатий?
-
При делении целых чисел на некоторое число можно получить столько различных остатков (включая и ноль), сколько единиц в делителе. Например, при делении на 5 остаток может быть равен нулю (число делится на 5), единице, двум, трем и четырем, то есть всего может быть пять различных остатков. Сколько нужно взять произвольных (наугад) целых чисел, чтобы среди них хотя бы два при делении на 3 давали одинаковые остатки?
-
Сколько надо цифровых знаков, чтобы пронумеровать тетрадь, в которой 10 страниц?
-
Малыш может съесть 600 г варенья за 6 минут, а Карлсон - в 2 раза быстрее. За какое время они съедят это варенье вместе?
-
Не выполняя деление, докажите, что число 7920 делится на 60.
-
При делении натурального числа на 2 получается в остатке 1, а при делении на 3 - в остатке 2. Какой будет остаток при делении этого числа на 6?
-
Сколько имеется четырехзначных чисел, которые делятся на 45, а две средние цифры у них 97?
-
Сколькими нулями оканчивается произведение 1*2*3*4*…*98*99*100?
-
Аня хочет положить в коробку одинаковое число своих игрушек. Сначала она попыталась разложить их по 12 в каждую коробку, но 5 игрушек остались лишними. Затем она попробовала разложить их по 15 в каждую коробку, но для последней коробки остались только 2 игрушки. Тогда Аня догадалась взять еще одну коробку. Сколько игрушек Аня теперь должна положить в каждую коробку, чтобы добиться своей цели?
Февраль
-
Найдите сумму двадцати чисел: 1, 2, 3,…., 18, 19, 20.
-
В школе 735 учащихся. Почему можно утверждать, что по крайней мере три ученика должны отмечать день рождения в один и тот же день?
-
С рынка возвращались две колхозницы. Одна из них спросила другую: «Что ты продавала?» Ответ был таким: «Я продавала дыни, и получилось так, что первый покупателю я продала половину всех дынь и еще полдыни, второму - половину оставшихся у меня дынь и еще полдыни. Третьему покупателю я продала также половину оставшихся после второго покупателя дынь и еще полдыни. Больше дынь у меня не осталось». Сколько же дынь продавала эта колхозница?
-
В пакете перемешаны конфеты трех сортов, не различимые на ощупь. Какое наименьшее число конфет надо взять наугад из пакета, чтобы среди вынутых конфет было хотя бы две конфеты одного сорта?
-
Двое детей по очереди (пропускать ход нельзя!) выставляют на стол либо одну фишку, либо столько, сколько их уже стоит на столе (если нужное число фишек еще осталось в коробочке). Выигрывает тот из них, кто поставит последнюю фишку. В начале игры на столе фишек нет, а в коробочке - 5. Кто выигрывает, если будет играть наилучшим образом?
-
Кирпич весит 1 кг и еще столько, сколько весит полкирпича. Сколько весит кирпич?
-
Найди дробь, у которой числитель больше знаменателя и которая не изменится, если ее перевернуть «вверх ногами».
-
Три одинаковых арбуза надо разделить поровну между четырьмя детьми. Как это сделать, выполнив наименьшее число разрезов?
-
Как от куска материи в
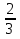 м отрезать полметра, не имея под руками метра?
м отрезать полметра, не имея под руками метра? -
Рыбак поймал рыбу. Когда у него спросили, какова масса пойманной рыбы, он сказал: «Я думаю, что хвост ее - 1 кг, голова столько, сколько хвост и половина туловища, а туловище - сколько голова и хвост вместе». Какова же масса этой рыбы?
Март
-
Коля, Вася, Балгабай играли в шашки друг с другом. Каждый из них сыграл 2 партии. Сколько всего партий было сыграно?
-
Собака погналась за лисицей, находящейся от нее на расстоянии 120 м. Через сколько времени собака догонит лисицу, если лисица пробегает в минуту 320 м, а собака 350 м?
-
В одном классе уроки математике, истории и русскому языку ведут три учителя: Архипов, Морозов и Сыздыков. Определите, кто из них какой предмет ведет, если известно, что: а) все трое - Морозов, учитель математики и Сыздыков - идут из школы домой вместе; б) учитель истории старше учителя математики, а Морозов - самый младший среди них.
-
Один биолог открыл удивительную разновидность амеб. Каждая из них через минуту делятся на две. В пробирку кладет одну амебу, и ровно через час вся пробирка оказывается заполненной амебами. Сколько потребовалось бы времени, чтобы вся пробирка заполнилась амебами, если бы в нее положили вначале не одну амебу, а две?
-
Сколько можно взять разных натуральных чисел, не больших 10, чтобы среди них не нашлось двух, одно из которых точно вдвое больше другого?
-
Как изменить число 666 в
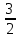 раза, не производя над ним никаких арифметических операций?
раза, не производя над ним никаких арифметических операций? -
Сократите дробь
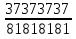 .
. -
В классе 36 учеников. Сколько среди них мальчиков и сколько девочек, если
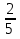 числа всех мальчиков равны половине числа всех девочек?
числа всех мальчиков равны половине числа всех девочек? -
Один тракторист мог бы вспахать поле за 10 часов, а другой (его ученик) - за 40 часов. За сколько часов вспашут поле два тракториста при совместной работе?
-
Два сосуда вместимостью 144 л и 70 л содержат некоторое количество воды. Если больший сосуд долить доверху водой из второго сосуда, то в последнем останется еще 1 л воды. Если же долить доверху меньший сосуд водой, то в большем останется
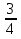 первоначального количества воды. Сколько литров воды содержится в каждом сосуде?
первоначального количества воды. Сколько литров воды содержится в каждом сосуде?
Апрель
-
Можно ли разменять купюру достоинством 50 тенге с помощью 15 монет достоинством 1 и 5 тенге?
-
Расшифруйте ребус: АБВ
+ ВВ
ААБ
-
Поезд проходит мост длиной 450 м за 45 секунд, а мимо столба - за 15 секунд. Вычислите длину поезда и его скорость.
-
Кондратьев, Давыдов и Федоров живут на одной улице. Один из них работает плотником, другой - маляром, третий - водопроводчиком. Однажды маляр пришел к плотнику, чтобы попросить его починить дверь в своей квартире, но ему сказали, что плотник помогает Федорову ремонтировать пол. Определите профессию каждого, если известно, что водопроводчик никогда не видел Давыдова.
-
Как разделить поровну между двумя семьями 12 л хлебного кваса, находящегося в двенадцатилитровом сосуде, воспользовавшись для этого двумя пустыми сосудами: восьмилитровым и трехлитровым?
-
Требуется полсотни разделить на половину. Сколько получится?
-
Вычислите:
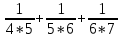 +
+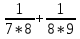 +
+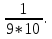
-
Автомобиль из А в В ехал со скоростью 50км/ч, а обратно возвращался со скоростью 30 км/ч. Какова его средняя скорость?
-
Вини - Пух съедает банку меда за 4 часа, а его друг Пятачок - за 5 часов. За какое время они съедят такую банку меда, если начнут со своей обычной скоростью есть ее вместе?
-
Некий человек на вопрос, сколько он имеет денег, ответил: «Аще придастся к моим деньгам толико же, елико имам, и полтолика, и
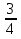 , и
, и 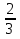 , и убавится из всего 50 рублев, и ведательно есть, колико той человек имяше денег». (Магницкий.)
, и убавится из всего 50 рублев, и ведательно есть, колико той человек имяше денег». (Магницкий.)
Май
-
Петя сказал однажды друзьям: «Позавчера мне было 9 лет, а в будущем году мне исполнится 12 лет». Какого числа родился Петя?
-
В 12 часов дня часовая и минутная стрелки часов совпадают. Через сколько минут после этого они снова совпадут?
-
В квадрат со стороной, равной трем тетрадным клеткам, бросили 10 точек. Докажите, что хотя бы в одной из клеток находятся 2 точки.
-
Из двух селений одновременно навстречу друг другу выехали два велосипедиста: первый со скоростью 20 км/ч, второй - 15 км/ч. Каким будет расстояние между ними за 2 часа до встречи?
-
Вымостите плоскость одинаковыми скобками из 6 квадратов (см. рис.)
-
Найдите двухзначное число, которое от перестановки его цифр увеличивается в 4,5 раза.
-
Винни - Пуху подарили в день рождения бочонок с медом массой 7 кг. Когда Винни - Пух съел половину меда, то бочонок с оставшимся медом стал иметь массу 4 кг. Сколько килограммов меда было первоначально в бочонке?
-
Лоси составляют
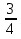 от общего числа косуль и лосей, которые живут в заповеднике. Сколько косуль живет в заповеднике, если число лосей на 144 меньше, чем количество косуль?
от общего числа косуль и лосей, которые живут в заповеднике. Сколько косуль живет в заповеднике, если число лосей на 144 меньше, чем количество косуль? -
Из корзины яиц взяли половину всего количества яиц, потом еще половину остатка, затем половину нового остатка и, наконец, половину следующего остатка. После этого в корзине осталось 19 яиц. Сколько яиц было в корзине первоначально?
-
Три хозяйки готовили обед в одной печи. Одна положила в огонь 4 полена, а вторая - 7. У третьей хозяйке дров не было, поэтому она дала двум первым гривенник (10 тенге) и тиын. Как они должны поделить эти деньги?
Раздел 6.Олимпиадные задания по математике 5-11 классов.
Сентябрь
-
Рассказывают, что в начальной школе, где учился мальчик Карл Гаусс, ставший потом знаменитым математиком, учитель,
Олимпиадные задания по математике 5 класс /школьный тур/
1.На прямой линии посажено 10 кустов так, что расстояние между любыми соседними кустами одно и то же. Найдите это расстояние, если расстояние между крайними кустами равно 90 дм.
-
Угадайте корень уравнения и сделайте проверку:
Х*Х+5=21
3. В записи 1*2*3*4*5 замените * знаками действий и расставьте скобки так, чтобы получилось выражение, значение которого равно 100.
4. Было 9 листов бумаги. Некоторые из них разрезали на три части. Всего стало 15 листов. Сколько листов бумаги разрезали?
5. Для нумерации страниц книги потребовалось 1392 цифры. Сколько страниц в книге?
Олимпиадные задания по математике 6 класс /школьный тур/
-
Поставьте вместо звездочек цифры:
59,27
+ **,45
78,*3
182,1*
-
К числу 15 припишите слева и справа по одной цифре, чтобы оно делилось на 15.
-
Найдите все дроби со знаменателем 15, которые больше 8/9 и меньше 1.
-
5. В летний лагерь приехали отдыхать три друга: Миша, Володя и Петя. Известно, что каждый из них имеет одну из следующих фамилий: Иванов, Семенов, Герасимов. Миша -не Герасимов, отец Володи -инженер. Володя учится в 6 классе. Герасимов учится в 5 классе, Отец Иванова-учитель. Какая фамилия у каждого из трех друзей?
-
Для нумерации страниц книги потребовалось 1392 цифры. Сколько страниц в книге?
Олимпиадные задания по математике 7 класс /школьный тур/
-
Число 2012ав делится на 18. Найдите все такие числа.
-
На складе имеются гвозди в ящиках по 24 кг, 23 кг, 17 кг и 16 кг. Может ли кладовщик отпустить со склада 100 кг гвоздей , не распечатывая ящики?
-
Сколько шестизначных нечетных чисел можно составить из цифр 0. 2, 1, 5 и 6?
-
Разрежьте квадрат на четыре треугольника и квадрат. Укажите разные способы решения задачи.
-
/Старинная задача Л.Ф. Магницкого/
Спросил некто учителя: «Сколько у тебя в классе учеников, так я хочу отдать к тебе в учение своего сына?»
Учитель ответил: «Если придет учеников еще столько же, сколько имею, и полстолько, и четвертая часть, и твой сын, тогда будет у меня 100 учеников.» Сколько учеников было у учителя?
Олимпиадные задания по математике 8 класс /школьный тур/
1.Какой цифрой оканчивается значение выражения 32012
2. Сколько трехзначных чисел не содержат цифру 5?
3. Угол между высотой и биссектрисой прямоугольного треугольника, проведенных из вершины прямого угла , равен 120. Найдите острые углы данного прямоугольного треугольника.
4 Ивану сейчас в 4 раза больше лет, чем было его сестре Маше, когда она была моложе Вани в два раза. Сколько сейчас лет Ивану и его сестре, если через 15 лет им будет вместе 100 лет?
5. В выпуклом четырехугольнике АВСД диагональ АС является биссектрисой углов А и С , диагональ ВД- биссектриса углов В и Д. Докажите, что все стороны четырехугольника АВСД равны
Олимпиадные задания по математике 9 класс /школьный тур/
1.Решите уравнение: | 3х2 + 5х | =2
2.На столе стоят три совершенно одинаковых ящика. В одном из них лежит два черных шара, в другом- белый и черный, в третьем- два белых шарика. На ящиках сделаны надписи: «два белых», «два черных», «»Черный и белый». Известно, что ни одна из надписей не соответствует действительности, Как, вынув только один шарик , определить , где лежат какие шары?
3.Из пункта А в пункт В автобус едет со скоростью 90 км/ ч, на обратном пути из-за плохой погоды его скорость снизилась до 60 км/ч. Найти среднюю скорость движения на всем пути следования.
4.Для нумерации страниц некоторой книги использовано 6873 цифры. Сколько страниц в книге?
-
В выпуклом четырехугольнике АВСД диагональ АС является биссектрисой углов А и С , диагональ ВД- биссектриса углов В и Д. Докажите, что все стороны четырехугольника АВСД равны
Олимпиадные задания по математике 10 класс /школьный тур./
-
Решите уравнение
(х-2) (х-3) (х+4) (х+5) =1320.
-
В выпуклом четырехугольнике АВСД диагональ АС является биссектрисой углов А и С , диагональ ВД- биссектриса углов В и Д. Докажите, что все стороны четырехугольника АВСД равны
-
Для нумерации страниц некоторой книги использовано 6873 цифры. Сколько страниц в книге?
-
Найдите все трехзначные числа, которые в 12 раз больше суммы своих цифр
-
Путь из села в город таков: сначала 15 км в гору, потом 6 км с горы. Велосипедист едет без остановки в гору с одной постоянной скоростью, с горы - с другой. В один конец он ехал 3, 1 ч, обратно 2.5 ч. Какова скорость велосипедиста в гору и с горы?
Олимпиадные задания по математике 11 класс /школьный тур/
-
Найти наибольшее значение выражения х +у, где пара х, у- некоторые целочисленное решение уравнения
Х2 -3ху + 2у2 =7.
2. Найдите все трехзначные числа, которые в 12 раз больше суммы своих цифр
-
Путь из села в город таков:: сначала 15 км в гору, потом 6 км с горы. Велосипедист едет без остановки в гору с одной постоянной скоростью, с горы - с другой. В один конец он ехал 3, 1 ч, обратно 2.5 ч. Какова скорость велосипедиста в гору и с горы?
-
В треугольнике АВС проведены высоты АК и ВН, О-центр вписанной окружности, Доказать, что отрезки ОС и КН перпендикулярны.
-
Из 100 посетителей столовой не менее 60 человек купили себе на обед борщ, не менее 70 -плов, не менее 80 -чай. Какое минимальное количество человек купили себе все три блюда?
Раздел 7.Раскраски.
Использованная литература.
-
Математика 5 класс: И.И Зубарева,А.Г.Мордкович-М.:Мнемозина, 2012.
-
Алгебра открытые уроки: С.Н.Зеленская. Издательство «Учитель
-
Мордкович А.Г. Учебник математики 6 класс. - Москва: Мнемозина, 2009.
-
Мордкович А.Г. Математика 6 класс. Методическое пособие для учителя. - Москва: Мнемозина, 2009.
-
Мордкович А.Г. Математика. Тесты для 6 класса. - Москва: Мнемозина, 2008.
-
Семенова А.Л. и Ященко И.В. Рабочая тетрадь ЕГЭ 2010. - Москва: МЦНМО, 2010.
Интернет- ресурсы:
-
- «Одаренные дети»
-
- Википедия
-
- «ProШколу.ru»
-
-
http://www.uchportal.ru