- Учителю
- Конспект урока по алгебре 'Специальные методы решения квадратных уравнений' (8 класс)
Конспект урока по алгебре 'Специальные методы решения квадратных уравнений' (8 класс)
Тема урока: Специальные методы решения квадратных уравнений
Цель урока: 1. Создать условия для отработки практических умений и навыков по решению ных квадратных уравнений специальными методами.
2. Создать для учащихся оптимальные условия для развития аналитического и синтетического мышления, операционно-контрольных умений при решений квадратных уравнений, развития настойчивости, умении преодолевать трудности для достижения целей.
Тип урока: Урок применения знаний умении и навыков по решению квадратных уравнении.
Форма урока: практикум по решению задач.
Ход урока
-
Организационный момент
2. Актуализация знаний учащихся
І-этап
1) Историческая справка о квадратных уравнениях
Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными относятся во второму тысячелетию до н.э. Это эпоха расцвета Вавилонии и Древнего Египта.
Первое тысячелетие н.э. - Римские завоевательные войны. К этому периоду относится творчество Диофанта. Его трактат "Арифметика" содержит ряд задач, решаемых при помощи квадратных уравнений. Правило решения квадратных уравнений, приведенных к виду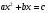 
, где a>0, дал индийский ученый Брахмагупта, живший в VII-веке. В IX веке хорезмский математик Аль-Хорезми в Трактате "Алгебра" классифицирует квадратные уравнения. Для нас это время знаковое тем, что приблизительно в это время образуется древнерусское государство Киевская Русь.
Все это время отличные по записи уравнения считались различными. Не было единого подхода к их решению.
Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. итальянским математиком Леонардом Фибоначчи.
И только в XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым заложил основы буквенной алгебры.
Учения об уравнениях есть одна из основных тем всей алгебры. С уравнениями мы сталкиваемся при решений вопросов химий, механики, астрономии.
Решение задач методом составления уравнении является могучим средством при решении многих вопросов производства, строительства и народного хозяйства. Современные вычислительные средства как микрокалькуляторы могут вычислять корны уравнения ax2+bx+c=0 по программе, основанной на формуле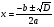 
.
Более подробно с этапами развития методов решения квадратных уравнений, а так же личностью Виета и его вклада в развитие алгебры мы сможем познакомиться на конференции.
II - этап.
2) Полиглот.
а) Выражение, с помощью которого определяют, имеет ли уравнение корни.
Латинское названия - дискриминант
Русский перевод - различитель
б) Величина, входящая в формулу или уравнение, значение которой является постоянная в пределах рассматриваемой задачи.
Греческое название - параметр
Русский перевод - отмеривающий
в) Числовой множитель одночлена, записанного в стандартном виде
Латинское название - коэффициент
Русский перевод - вместе в соединении
г) Один из способов изображения зависимости между величинами
Греческое название - диаграмма
Русский перевод - рисунок, фигура.
Какие основные способы решения квадратного уравнения вы знаете? (решение по формулам, теорема Виета)
3. Объяснение нового материала.
Сегодня на уроке мы рассмотрим специальные методы решения квадратных уравнений.
Я предлагаю вам отправится в путешествие на машине времени и посетить школу древних математиков. Но для этого нам необходим пригласительный билет.
3) Пригласительный билет
Уравнение
a
b
c
b2 - 4ac
x1
x2
x1+ x2
x1 · x2
x2- 7x + 12 = 0
5
-7
-6
5x2 = 15x
3
0
-75
Уравнение
a
b
c
b2 - 4ac
x1
x2
x1+ x2
x1 · x2
x2- 7x + 12 = 0
1
-7
12
1
4
3
7
12
5x2- 7x - 6 = 0
5
-7
-6
169
2
-0,6
1,4
-1,2
5x2 = 15x
5
-15
0
225
0
3
3
0
3x2 - 75 = 0
3
0
-75
900
5
-5
0
-25
Задания пишутся на карточках, проводится взаимопроверка групп.
Ну а теперь я предлагаю вам занять свои места в нашей машине времени и отправиться виртуальную школу.
Сценка «Спор математиков»
Поспорили как-то Диофант Александрийский и Виет, чей способ решения квадратного уравнения лучше.
- А я вам говорю, что если неопределенное уравнение имеет хотя бы одно рациональное решение, то таких решений будет бесчисленное множество, причем значения х и у могут быть представлены в виде рациональных функций некоторого параметра.
- Я с вами глубокоуважаемый в корне не согласен и помогут вам это доказать мои ученики.
Вы разделены на две группы. Одна группа будет учениками Диофанта Александрийского, а другая Виета. В каждой группе есть консультанты, которые помогут вам разобраться с методами. Итак, метод переброски коэффициентов.
(Ученица на доске комментирует метод и приводит решение).
- И всё - таки вы меня не убедили, посмотрите на мой метод решения.
На доске идёт представление метода решения квадратных уравнений с помощью свойств коэффициентов квадратного уравнения. Рассматриваются примеры.
- Уважаемый, ваш способ не приемлем.
-Нет, ваш.
- Мы в тупике. Необходима помощь в решении нашего вопроса. Давайте спросим у аудитории кто прав?
4. Закрепление нового материала.
- Мы рады помочь в решении вашего спора, но ответить на этот вопрос мы сможем лишь попробовав применить эти способы к решению уравнений.
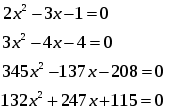
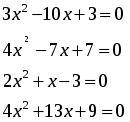
- Давайте ответим на вопрос наших математиков: Какой из представленных способов решения квадратных уравнений является универсальным? (Ни один из них не является универсальным, поэтому они носят название специальные).
5. Домашняя работа.
В качестве домашней работы я предлагаю вам:
1. Составить по 10 уравнений на применение каждого из разобранных сегодня способов.
2. Решить задачу Бхаскары.
6.Подведение итогов урока.
Вы сегодня очень хорошо поработали. Спасибо за урок.