Обощающий урок по математике в 11 классе «Решение логарифмических уравнений и неравенств» с использованием ИКТ

Конспект обобщающего урока по алгебре и началам анализа.

Уразова Людмила Михайловна

учитель математики высшей категории

МОУСОШ №7 г.Каменки Пензенской области

Тема: «Решение логарифмических уравнений и неравенств»

Форма урока: урок с использованием информационных технологий

Тип урока: обобщение и закрепление пройденного материала.

Цель урока: Обобщить знания по теме, сформировать умения решать логарифмические уравнения и неравенства.

Задачи:

• учебные: углубить теоритические знания решения логарифмических уравнений и неравенств;

• развивающие: развивать умения применять знания на практике; формировать умение выделять существенное, главное; развивать стремление к расширению знаний;

• воспитывающие: воспитывать у учащихся разнообразные интересы и способности..

Оборудование: интерактивная доска, компьютеры, карточки-памятки.

Ход урока.

1. Организационный момент.

Вступительное слово учителя: Я хочу начать урок со слов французского писателя Анатоля Франца «Учиться можно только весело…Чтобы переваривать знания, надо поглощать их с аппетитом»

Давайте же и мы последуем совету писателя, и будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они скоро вам понадобятся при сдаче ЕГЭ.

Перед вами стоит задача - повторить способы и приёмы решений логарифмических уравнений и неравенств.

2. Устный опрос.

Учитель: Скажите, что такое логарифм. Для того, чтобы было легче решать уравнения, вы должны уметь вычислять логарифмы. ( слайд с устными упражнениями)

Учитель: У вас на партах лежат памятки с методами решений логарифмических уравнений и неравенств. Рассмотрите первый метод «По определению». Из предложенных уравнений (слайд с уравнениями) выберете те, которые решаются этим методом и решите.

Аналогично рассматриваются все методы решения.

3. _{Самостоятельная работа (с последующей самопроверкой)}

_{Учитель: А теперь я предлагаю вам пройти тестирование в режиме онлайн на uztest.ru. Каждый ученик на персональном компьютере проходит тестирование, по окончанию учитель на экран выводит результаты каждого. Разбирают ошибки.}

4. _{Работа по углублению знаний учащихся (подготовка к ЕГЭ).}

_{Учитель: Предлагаю перейти к логарифмическим неравенствам. Это как раз то, с чем вам придётся иметь дело на ЕГЭ по математике в заданиях С3. Скажите какой теоремой мы пользуемся при решении неравенст? (Если f(x)>g(x), то при a>1 logaf(x)>logag(x) , если…..) Предлагаю решить неравенство.}

_logx(x²_{-3)<0. (Учащийся у доски решает традиционным способом)}

_{Учитель: Ребята, я хочу познакомить вас со способом рационализации, который позволяет сложное выражение F(x) заменить более простым G(x) так. Что F(x)>0 равносильно G(x)>0 на области определения F(x).}

_{Изложение теоретического материала.}

_{Выделим некоторые выражения F и соответствующие им рационализующие выражения G,где u,v,,p,q-выражения с двумя переменными (u>0;u≠1;v>0,>0) ,а- фиксированное число ( а>0,a≠1).}

№

ВыражениеF

ВыражениеG

1

-

1a

1б

2

-

2a

2б

3

4

(

4a

5

6

Учитель: Посмотрите, как это неравенство решается, используя метод рационализации.

_logx(x²_-3)<0

Решение: ОДЗ : х;

Используем формулу 2б, получим (x-1)(x²-3-1)<0; (x-1)(x-2)(x+2)<0. Решая методом интервала и учитывая ОДЗ, получаем

Учитель: Предлагаю решить неравенство уровня С3, используя метод рационализации.

log_2x(2x²-4x+6)log_2x(x²+x)

5. Подведение итога урока. Учитель: Мы рассмотрели с вами применение метода рационализации при решение логарифмических неравенств. Этот метод широко применяется при решение неравенств разных видов при решение экзаменационного материала типа С3. На следующем уроке мы рассмотрим применение этого метода при решение показательных неравенств и иррациональных.

6. Задание на дом. Задание дается по рядам из книги «Математика ЕГЭ 2013» (типовые задания С3) или на сайте

Способы решения логарифмических уравнений.

1) По определению.

Простейшее логарифмическое уравнение x)=b

ОДЗ:

1. f(x)=a^b (по определению логарифма)

2. отбор корней, удовлетворяющих ОДЗ

3. По теореме (потенцирование).

x)=x)

ОДЗ:

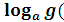
1. Решить f(x)=g(x)

2. отбор корней, удовлетворяющих ОДЗ

3) Метод введения новой переменной.

ОДЗ:

Пусть t=x)

at² + bt + c =0

Решим квадратное уравнение

D = b² - 4ac

t_{1 =} ; t_{2 =}

x)= t₁ x)= t₂

4) Метод логарифмирования.

=b

ОДЗ:

1. Обе части уравнения прологарифмируем по основанию a

2. отбор корней, удовлетворяющих ОДЗ

5) Переход к новому основанию.

Если в уравнении логарифмы с разными основаниями

Пример

x)=x)

ОДЗ:

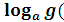
1. Сведите логарифмы к одному основанию

2. отбор корней, удовлетворяющих ОДЗ