Конспект урока по алгебре для учащихся 8 класса по теме «Обратная пропорциональность и её график»

Конспект урока по алгебре для учащихся 8 класса по теме «Обратная пропорциональность и её график»

Цель урока:

Образовательная: познакомить учащихся с понятием функции обратной пропорциональности, её графиком; научить работать с функцией 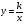и её графиком в процессе решения задач.

Задачи:

• повторить понятие функции;

• познакомить с понятием функции обратной пропорциональности и ее графиком;

• научить решать задачи по данной теме.

Развивающая: развивать логическое мышление, память, внимание, формировать умения анализировать, сопоставлять данные, выводить логические следствия из данных предпосылок, умение делать выводы.

Воспитательная: воспитывать сознательное отношение к учебному труду, самостоятельность, прививать аккуратность и трудолюбие.

Тип урока: урок усвоения новых знаний.

Требования к ЗУН:

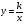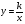учащиеся должны знать определение функции обратной пропорциональности, свойства функции при , при .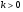

учащиеся должны уметь работать с формулой и графиком функции обратной пропорциональности, решать задачи с их использованием.

Методы обучения: индуктивно-эвристический, дедуктивно-репродуктивный.

Оборудование: компьютер, экран, проектор, мультимедиа презентация.

Литература:

1. Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков и др. - 11-е изд. - М. : Просвещение, 2010.- 384 с.

2. Дидактические материалы по алгебре 8класс: кн. для учителя/В.И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк.-М. Просвещение,2007,-144с.

3. Контрольные и проверочные работы по алгебре в 7-9 классах: кн. для учителя / Л. И. Звавич, Л.Я. Шляпочник. М. Дрофа, 2002,-96с.

План урока:

1. Организационный момент (2 минуты)

2. Актуализация знаний (5 минут)

3. Изучение нового материала (12 минут)

4. Закрепление изученного материала (21минута)

5. Домашнее задание (2 минуты)

6. Подведение итогов (3 минуты)

Ход урока

Организационный момент

Включает в себя приветствие учителем класса, проверку готовности кабинета к проведению урока, проверку отсутствующих.

Актуализация знаний

Учитель: На сегодняшнем уроке мы приступаем к изучению новой темы «Обратная пропорциональность и её график». Мы познакомимся с понятием функции обратной пропорциональности, её графиком. Научимся решать задачи. (Слайд 1)

Учитель: Начнем урок с повторения материала, изученного на прошлом уроке. Я прошу вас обратить внимание на доску: на слайде записаны вопросы. Необходимо ответить на них. (Слайд 2)

Учащиеся по очереди отвечают на вопросы.

Учитель: Как называется функция вида y = kx + b?

Ученик: Функция вида y = kx + b называется линейной.

Учитель: Как называется линейная функция вида y=kx?

Ученик: Линейная функция вида y=kx называется прямой пропорциональностью.

Учитель: Что называется асимптотой кривой?

Ученик: Асимптотой кривой называется прямая, к которой приближаются как удобно близко точки кривой при удалении их в бесконечность.

Учитель: Что является графиком функции ?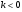

Ученик: Графиком функции 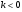является гипербола.

На слайде появляются ответы (Слайд 3).

Изучение нового материала

Учитель: Мы с вами немного повторили предыдущий материал, а теперь откройте свои тетради и запишите число, классную работу и тему урока «Обратная пропорциональность и её график».

Запись на доске (слайд 4) и в тетрадях:

Запись в тетради:

Число

Классная работа.

Тема урока: «Обратная пропорциональность и её график».

Учитель: Рассмотрим функцию 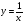при k > 0, где независимая переменная х принимает положительные значения. И говорят, что переменная у обратно пропорциональна переменной х, а саму функцию называют обратной пропорциональностью. (Слайд 5)

Учитель: Обратная пропорциональность находит широкое применение на практике.

Например:

1. время, затраченное на прохождение одного и того же пути, обратно пропорционально скорости движения;

2. количество товара обратно пропорционально цене этого товара при одной и той же сумме денег, затраченных на его покупку;

3. количество товара обратно пропорционально цене этого товара при одной и той же сумме денег, затраченных на его покупку. (Слайд 6)

Учитель: А теперь построим график функции 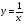. Запишите в свои тетради данное задание со слайда. (Слайд 7)

Запись в тетрадях: Построить график функции .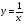

Учащиеся вместе с учителем разбирают пример построения графика функции 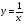, отвечают на наводящие вопросы и делают записи в тетради.

Учитель: Что необходимо сделать для построения этого графика?

Ученик: Для построения графика 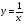следует вычислить координаты нескольких точек графика, построить их и через них провести плавные линии.

Учитель: Чему равен k, в данной функции?

Ученик: k=6

Учитель: Верно, значит 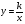. Составим таблицу положительных значений аргумента. В своих тетрадях начертите таблицу.

Запись в тетрадях:

Учитель: Если аргумент х примет значение 1, то чему будет равно значение функции у?

Ученик: Значение функции у будет равно .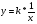

Запись в тетради: у=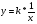

Учитель: Верно. Найдите для указанных значений аргумента соответствующие значения функции и постройте прямоугольную систему координат.

Запись в тетрадях:

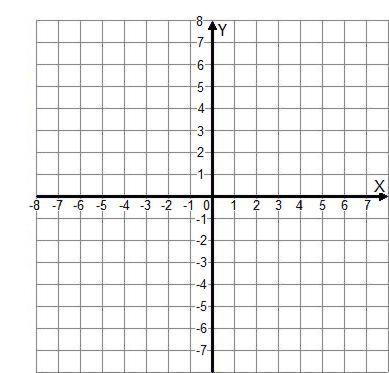
Учитель: Мы получили 6 пар точек. Назовите мне их.

Ученик: (1;6), (2;3), (3;2), (4; 1,5), (5;1,2), (6;1).

Учитель: Правильно, а теперь назовите точки с противоположными координатами, для построения графика функции 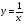_{поскольку им является гипербола, а для её построения необходимы точки с противоположными координатами.}

Ученик: (-1;-6), (-2;-3), (-3;-2), (-4; -1,5), (-5;-1,2), (-6;-1).

Учитель: Все верно. Теперь давайте построим полученные пары точек. Первая точка имеет координаты (1;6). Находим эту точку и отмечаем. Проделайте эту операцию с остальными точками.

(Учащиеся строят точки на прямоугольной системе координат в своих тетрадях).

Учитель: Теперь последовательно соедините построенные вами точки плавной линией. У вас должна получиться кривая, состоящая из двух ветвей.

Запись в тетрадях:

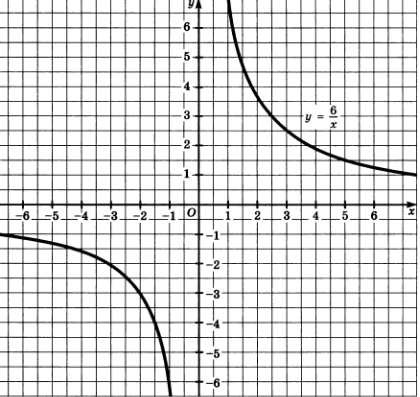
Учитель: Итак, мы получили график функции .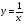

Учитель: Сверьте график, который вы получили, с графиком, представленным в учебнике (рис. 67).

Учитель: Прочитайте определение обратной пропорциональности со слайда. (Слайд 8)

(Учитель просит одного из учеников озвучить определение вслух)

Ученик: Обратной пропорциональностью называется функция, которую можно задать формулой 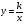, где х - независимая переменная и k - не равное нулю число.

Число k называют коэффициентом обратной пропорциональности.

Учитель: Вы знаете, что график функции 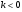- гипербола. График функции 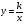также называют гиперболой. Следовательно, полученный нами график функции 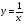- гипербола.

Закрепление изученного материала

Учитель: А теперь перейдем к выполнению заданий. (Слайд 9)

Учащиеся выходят по очереди к доске, решают примеры, комментируют решение, остальные - решают на месте, делая записи в тетради.

Учитель: Перепишите задание в тетради со слайда. Для тех, кто понял, как строятся графики, я запишу на доске номера из учебника, которые вы можете решать вперед нас.

Запись на доске: № 1245; №1244 (а); № 1247.

Запись на доске и в тетрадях: № 1245

Построить график функции .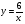

Учитель: Первый номер № 1245.

Учитель: Что нужно сделать по условию задачи?

Ученик: Нужно построить график функции .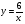

Учитель: Чему равен коэффициент k?

Ученик: k= -12, где .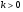

Учитель: С чего начнём построение графика?

Ученик: Сначала зададим таблицу значений.

Учитель: Составьте таблицу значений в тетрадях.

Запись на доске и в тетради:

Учитель: Теперь для данных значений аргумента, найдем значения функции и занесем их в таблицу.

Учитель: Если аргумент примет значение -12, то чему будет равно значение функции?

Ученик: Значение функции будет равно .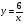

Учитель: Верно. Найдите для указанных значений аргумента соответствующие значения функции.

Запись на доске и в тетради:

х

-12

-6

-4

-3

-2

-1

у

1

2

3

4

6

12

Учитель: Назовите точки, координаты которых записаны в таблице и точки с противоположными координатами, для построения графика функции 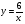_{поскольку им является гипербола, а для её построения необходимы точки с противоположными координатами.}

Ученик: (-12;1), (-6;2), (-4;3), (-3;4), (-2;6), (-1;12), (12;-1), (6;-2),(4;-3), (3;-4), (2;-6), (1;-12).

Учитель: Постройте прямоугольную систему координат и отметьте на ней эти точки, после соедините эти точки плавной линией.

Запись на доске и в тетради:

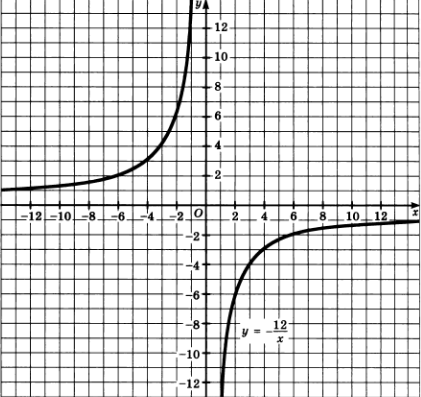
Учитель: А теперь обратите внимание на доску и проверьте, верно ли вы построили график. У вас должна получиться кривая, состоящая из двух ветвей.

На слайде появляется решение, с которым учащиеся сверяют свою запись. (Слайд 9)

Учитель: Хорошо. Следующий номер №1244 (а) (Слайд 10)

Запись на доске и в тетради: № 1244 (а)

Учитель просит ученика прочитать задание со слайда.

(Ученик читает задание, все остальные слушают его).

Ученик: Используя график 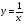(см. рис. 67), найдите: значение у, соответствующее значению х, равному 1,5; 2,5; -1,5; -4,5.

Учитель: Перерисовывать график 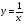не будем. Пользуясь этим графиком, находим значение у по заданному значению х. Находим на графике значение х = 1,5, и определяем для этого значения у. Мы видим, что у = 4. Следующее значение х=2,5, определяем для этого значения у=3. А чему будет равен у для остальных значений х?

(Учитель спрашивает одного из учеников)

Ученик: Если х= -1,5, то у=-4; если х=-4,5, то у=-1,5.

Запись на доске и в тетради:

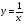(см. рис. 67), найти: значение у, соответствующее значению х, равному 1,5; 2,5; -1,5; -4,5.

Решение:

Если х=1,5, то у=4;

Если х=2,5,то у=3;

Если х= -1,5, то у=-4;

Если х=-4,5, то у=-1,5.

Учитель: Верно. Сверьте свои ответы, с ответами, представленными на слайде.

На слайде появляются ответы (слайд10).

Учитель: Все справились с заданием. Теперь решим номер №1247. (Слайд11)

Запись на доске и в тетрадях: №1247 (а, б, в, г)

Учитель просит ученика прочитать задание со слайда.

Ученик: На рисунке 71 построен график некоторой функции. Определите, принадлежит ли графику функции, точка:

а) А (-1;-4); б) В (1;-2)

в) С (3;5) г) D (-4;1,5)

Учитель: График представлен на слайде и в учебнике, на странице 338.

Запись на доске и в тетради:

Определить, принадлежит ли графику функции, точка:

а) А (-1;-4); б) В (1;-2)

в) С (3;5) г) D (-4;1,5)

Учитель: Пользуясь данным нам графиком, находим точку А с координатами (-1;-4), где значение х=-1, а у=-4. И видим, что точка А (-1;-4) принадлежит данному графику, так как она лежит на одной из ветви гиперболы. Будут ли принадлежать точки В, С, D данному графику?

(Учитель спрашивает одного из учеников)

Ученик: Точка В с координатами (1;-2) и точка С (3;5) не принадлежат графику функции. А точка D (-4;1,5) принадлежит, так как она лежит на ветви гиперболы.

Запись на доске и в тетради:

Решение:

(рисунок 71 стр. 338)

а) Точка А (-1;-4) принадлежит графику функции;

б) Точка В (1;-2) не принадлежит графику функции;

в) Точка С (3;5) не принадлежат графику функции;

г) Точка D (-4;1,5) принадлежит графику функции.

Учитель: Все верно, вы успешно справились с заданием. Ребята, которые выполняли задания вперед, подойдите после урока на проверку решения задач. Я поставлю Вам дополнительные оценки.

Домашнее задание

Учитель: Открываем свои дневники и записываем домашнее задание. (Слайд 12)

Запись в дневниках: №1245, №1246, №1249.

Подведение итогов

Учитель: На сегодняшнем уроке мы познакомились с определением обратной пропорциональности, научились решать задачи по данной теме. А кто сможет повторить определение обратной пропорциональности?

(Ученики поднимают руки, учитель спрашивает одного из них)

Ученик: Обратной пропорциональностью называется функция, которую можно задать формулой 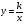, где х - независимая переменная и k - не равное нулю число.

Учитель: Молодцы! Я надеюсь, что вы освоили сегодняшний материал.

(В конце урока учитель выставляет оценки учащимся)