- Учителю
- Конспект олимпийского урока математики по теме: «Действия с положительными и отрицательными числами». (6 класс)
Конспект олимпийского урока математики по теме: «Действия с положительными и отрицательными числами». (6 класс)


 План урока математики в 6 классе.
План урока математики в 6 классе.
Тема: «Действия с положительными и отрицательными числами».
Цели:
1. Закреплять вычислительные навыки при выполнении действий с положительными и отрицательными числами.
2. Развивать наблюдательность и сообразительность у учащихся; прививать интерес к математике.
3. Показать связь математики и спорта.
Ход урока.
I. Организационный момент.
II. Устный счет.
1. Задумайте число, прибавьте к нему 500, полученную сумму удвойте, вычтите задуманное число, прибавьте 7, вычтите задуманное число. Полученный результат умножьте на 2. Результат внесите в лист заданий.
(2014).
-Чем запомнится нам это год?
Слайд №1.
2. Отгадаем некоторые зимние виды спорта. Для этого надо решить примеры и по результатам расшифровать названия.
Презентация №1
а) Биатлон, керлинг, бобслей.
б) Керлинг.
Этот вид спорта узнали сравнительно недавно. Со стороны такое зрелище поначалу кажется непонятным, смешным и даже глупым. Но знатоки любят говорить, что керлинг - ледовые шахматы.
Кёрлинг возник в Шотландии в начале XVI века, фактическим подтверждением существования этой спортивной игры является кёрлинговый спортивный снаряд (камень), найденный на дне осушенного пруда в Данблейне. На поверхности этого камня выбита дата его изготовления, узнайте её, найдя по цифрам четырехзначное число.
Первая цифра - число противоположное -1.
Вторая цифра - является числом, взаимно обратным числу 1/5.
Третья цифра - самое маленькое натуральное число.
Четвертая цифра - результат сложения -25 и 26. (1511).
в) Кёрлинг представляет собой спортивную игру на льду, в которой участвуют две команды. Участники поочерёдно пускают по льду гранитные снаряды («камни») в сторону размеченной на льду мишени («дома»). Цель игры - попасть камнем ближе к центру «дома», чем это сделал соперник.
Кёрлинг был признан олимпийским видом спорта в 1998 году на зимней Олимпиаде в Нагано (Япония).
Определите год, в котором наша женская сборная по кёрлингу впервые приняла участие в зимней Олимпиаде: найдите четырёхзначное число, которое является числом- палиндромом и составлено только из цифр 0 и 2.
Палиндромами называются числа, которые одинаково читаются слева направо и справа налево.
III. Решение задач.
1. Длина окружности камня не должна превышать 36 дюймов, а высота камня должна составлять не менее 4,5 дюймов. Выразите длину окружности камня и его высоту в сантиметрах, считая, что 1 дюйм = 2,54
см.
2. Масса камня, включая ручку и винт, не должна превышать 44 фунта и должна быть не менее 38 фунтов. Выразите массу камня - в килограммах.
3. Площадка для игры в кёрлинг
Длина площадки для кёрлинга составляет 45,72 м, ширина - не более 5 метров. Эта область ограничена начерченными линиями или
специальными разделителями, размещёнными по периметру. Если существующая ледовая арена не позволяет использовать эти размеры, то длина может быть уменьшена до 44,501 м, а ширина до 4,42 м. Найдите максимальную и минимальную площадь ледовой площадки.
IV Физминутка.
V. Математика и спорт.
Есть ли связь?
Немало интересных закономерностей математики обнаружили в спорте. В числе прочего они объяснили, почему левши имеют преимущество при игре в бейсбол, вывели связь между длиной пятки и спринтерскими качествами спортсмена, определили идеальную форму шара для гольфа и разработали наиболее эффективную тактику удара клюшкой.
Ещё в 1660 году великий мастер фехтования испанец Луис Пачеко де Нарваес развил теорию фехтования, основанную на математических принципах, в книге «Великие шаги». Он писал, что геометрия способствует тому, чтобы фехтовальщик понимал, какие положения тела, руки или меча будут наиболее эффективны в соответствии с положениями тела, руки или меча противника.
Знания математики и физики необходимы и игрокам в керлинг.
Очевидно, математика используется в каждом виде спорта. Тренер без математики не вырастит спортсмена-чемпиона.
«Как воздух, математика нужна
Любому человеку всей планеты,
Считать пельмени, доллары считать
И в космос запускать ракеты.
Как воздух, физкультура нам нужна -
Царицы всех наук для жизни мало.
Коль еле ходишь, плохо спишь,
Ты не изучишь интегралы…»
VI. Самостоятельная работа.
Задания разбиты по сложности на три уровня. Учащиеся самостоятельно выбирают себе задание
VII. Итог урока.
Ах, эта математика -
Наука очень строгая.
Учебник математики
Всегда берешь с тревогою.
Там функции и графики
И уравнений тьма,
А модуль может запросто
Свести тебя с ума.
И правила, и формулы,
Все так легко забыть,
Но все ж без математики
Нам невозможно жить.
Любите математику
И вы поймете вдруг,
Что, правда: "Математика - Царица всех наук!"
Приложение:
Лист заданий и ответов. __________________________________
1.
1
2
3
4
5
6
7
2-А 1) - 7,4 - 2,6 =
2) 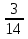 -
- 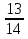 =
=
3) - 20,6 + 5,6 =
4) - 3,2 • 5 =
5) - 2,4 : (-8) =
6) - 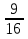 •
• 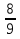 =
=
7) - 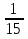 : (-
: (- 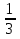 ) =
) =
3)
4)


