Урок геометрии на тему 'Тема урока: «Медиана, биссектриса и высота треугольника» (7 класс))

Тема урока: «Медиана, биссектриса и высота треугольника»

Цели урока:

1. Введение новых понятий высоты, медианы и биссектрисы треугольника.
2. Развитие логического мышления учащихся.
3. Формирование устойчивого познавательного интереса к изучению геометрии.
4. Развитие интеллекта, любознательности учащихся.
5. Развитие мышления через умение обобщать и систематизировать, доказывать и опровергать.
6. Формировать качества мышления, необходимые для продуктивной жизни в обществе.
7. Воспитывать культуру математического мышления, положительного эмоционального отношения к математике, аккуратность.
Оборудование и наглядность урока.

1. Модели треугольников, изготовленные из плотного цветного картона, с закреплёнными в вершинах цветными тесёмками (для каждого ученика и учителя).

2. Презентация к уроку «Медиана, биссектриса и высота треугольника».

3. Компьютер с мультимедийным проектором.

I. Сообщение темы урока и постановка задач урока.

Тема сегодняшнего урока: "Медиана, биссектриса и высота треугольника".

На уроке мы узнаем много нового и интересного о таких понятиях как медиана, высота и биссектриса треугольника.

Поучимся их строить в треугольнике и узнаем какое загадочное свойство они в себе хранят.

Итак, откройте тетради, запишем число и тему урока.

Какая геометрическая фигура изображена на весёлом рисунке? (Треугольник).

- А что называется треугольником?

(Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).

- Сколько у него элементов? (6)

- Назовите элементы треугольника. (Три стороны и три угла).

- Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты?

(Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида).

- А ведь знакомый всем нам треугольник таит в себе немало интересного и загадочного.

Зовётся он треугольник,
И с ним хлопот не оберётся школьник!

II. Объяснение нового материала.

1. Медиана.

Начертите треугольник АВС и найдите середину стороны ВС - точку Е.

Что называется серединой отрезка?

(Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).

Запись на доске: ВЕ=ЕС.

Соедините точку Е с вершиной А. Отрезок АЕ называется медианой треугольника.

Определение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Медиана-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас

Сколько вершин у треугольника? (3).

Сколько у него сторон? (3).

Сколько медиан можно провести в треугольнике?(3).

"Проведите" три медианы на моделях треугольников.

Какое свойство медиан вы заметили?

В любом треугольнике все медианы пересекаются в одной точке.

Эта точка называется центром тяжести треугольника.

Если «одеть» центр треугольника на спицу, то он будет находиться в равновесии.

2. Высота

С помощью чертёжного угольника из вершины В треугольника АВС проведём перпендикуляр ВН к прямой АС.

Он называется высотой треугольника.

Определение. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.

Сколько высот имеет треугольник? (3).

"Постройте" все три высоты на модели вашего треугольника.

- Обладают ли высоты аналогичным свойством, что и медианы? (Да).

Изобразим прямоугольный треугольник.

Где пересекаются его высоты?

(В вершине прямого угла).

Начертите треугольник АВС, у которого угол В - тупой. С помощью чертёжного угольника проведите его высоты.

Вывод. Высоты или их продолжения пересекаются в одной точке.

Эта точка называется ортоцентром.

Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.

Конечно, геометрия - наука серьёзная, и учить её надо серьёзно и вдумчиво. Но и забавные стихи и весёлые "геометрические" зверята помогают учению.

(показ слайда)

3. Биссектриса.

Вспомните определение биссектрисы угла.

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.

Запись на доске: АВК = СВК К АС.

Постройте биссектрису ВК угла В с помощью транспортира. Она пересечёт отрезок АС в точке К. Отрезок ВК называется биссектрисой угла В треугольника АВС.

Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.

Биссектриса - это крыса,
Которая бегает по углам
И делит угол пополам.

Покажите все три биссектрисы на вашей модели треугольника.

Сформулируйте свойство биссектрис треугольника.

В любом треугольнике биссектрисы пересекаются в одной точке(слайд)

III. Закрепление изученного материала
№ 1 Решение задачи по готовому чертежу (с комментированием).

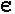
Дано:АВK, АВ = АК, АС - биссектриса А.
Доказать: АВС = АКС.
Решение:
АС - биссектриса А, ВАС = КАС;
АВ = АК (по условию), АС - общая сторона,

АВС = АКС по двум сторонам и углу между ними.

2. Работа в парах.

На каждой парте лежат три треугольника, разносторонние, разных цветов. На одном из них изображены три медианы, на другом - высоты, на третьем - биссектрисы.

1. Покажите треугольник с изображением высот. ( Фиолетовые и красные).

2. Поднимите треугольник, на котором изображены медианы.

3. Покажите треугольник с изображением биссектрис. (Зелёные, чёрные).

(Учащиеся поднимают треугольники).

Тест

1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.

а) Отрезок, соединяющий вершину треугольника с серединой ___________________ стороны, называется ______________ треугольника.

Б) Перпендикуляр, проведённый из ____________ треугольника к _________,

Содержащий противоположную сторону, называется ________________ .
2. Верны ли следующие утверждения? (В случае "нет" напишите верный ответ).

а) В любом треугольнике можно провести три медианы. (_____).
б) Точка пересечения высот любого треугольника всегда лежит внутри треугольника. (Не всегда).
в) Все биссектрисы треугольника пересекаются в одной точке. (_____).

Центр тяжести треугольника, его ортоцентр и точка пересечения биссектрис треугольника называются (особыми) замечательными точками треугольника.

Замечательные точки есть у треугольника.
Точка первая - она
Чувством гордости полна:
Медианы в ней пересекаются,
Центром тяжести та точка называется.
Ортоцентр - вторая точка,
Архимед её открыл,
Все высоты в ней встречаются,
Удивив учёный мир.
Третья точка - тоже важная
Биссектрисы всех углов,
Бросив вызов свой отважный,
В ней "сошлись", не тратя слов.
Эйлер точки все заметил,
Свойства новые открыл, -
Так на радость школьникам
Возникла Геометрия треугольника.

Итог урока

С какими новыми геометрическими понятиями вы сегодня познакомились? (Медиана, биссектриса, высота).

Три девицы, три сестрицы
В треугольнике живут.
Но вас предупреждаю я:
У каждой миссия своя!
Знает каждый школьник,
Как меня построить.
К чему не проведут меня,
Всем перпендикулярна я.
Отгадай, вопрос простой,
Как зовусь я? (Высотой).

Вначале вы найти должны
Середину стороны.
Ее соединишь с вершиной,
И меня уж получил ты.
Просто все и без обмана.
Как зовусь я? (Медиана).

IV. Домашнее задание. Стр. 33- 34, № 101, 102, 106.

Выставление отметок.