- Учителю
- Открытый урок по математике в 7 классе. Тема
Открытый урок по математике в 7 классе. Тема
16.12.2014. Тема урока «Умножение одночлена на многочлен»
Тип урока: Изучение нового материала
Оборудование и материалы: доска, раздаточный материал.
Оформление доски:
Эпиграф
"Незнающие пусть научатся, знающие - вспомнят еще раз.
Античный афоризм".
Анонс урока:
-
Распределительное свойство;
-
Кроссворд;
-
Умножение одночлена на многочлен;
-
Опорный конспект;
-
Упражнения.
Цели урока:
Методическая:
-
организовать работу класса по обобщению распределительного свойства.
Образовательная:
-
применение распределительного свойства к умножению одночлена на многочлен;
-
применение алгоритма на практике.
Развивающая:
-
формирование приемов логического мышления, умения анализировать;
-
развитие наблюдательности.
Воспитательные:
-
воспитание аккуратности;
-
воспитание привычки - доводить начатое до конца.
ХОД УРОКА
I. Организационный этап.
Эпиграф: "Незнающие пусть научатся, знающие - вспомнят еще раз.
Античный афоризм."
Мы вернемся к записанным словам в конце урока и сделаем для себя важный вывод, что наблюдательность дает повод для применения уже имеющейся информации.
II. Актуализация опорных знаний в форме устной работы.
1. Решим устно задачи:
а) Двое рабочих изготавливают одинаковые детали. Один рабочий делает за час 27 деталей, а другой - 32 детали. Продолжительность рабочей смены 8 ч. Что означают выражения -
(27 + 32) * 8 и 27 * 8 + 32* 8
Какой вывод можно сделать?
б)
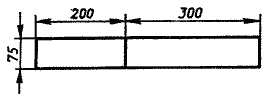
Опытный участок шириной 75 м разделен на две части. Длина одной части 200 м, а другой - 300 м. Что означают выражения -
(200 + 300) * 75 и 200 * 75 + 300 * 75
Какой вывод можно сделать?
Вопрос: Какой вопрос вы бы поставили и в первой, и во второй задаче, чтобы алгоритм решения был одинаков.
2. А теперь письменно в тетради выполним следующую задачу:
Туристы были в пути 3 ч. утром и 4 ч. вечером, причем скорость их была постоянной - 5 км/ч. Составьте выражение для вычисления пройденного пути за день и вычислите его значение.
Вопрос: Что общего в этих трех задачах?
Вывод: Решение по схеме
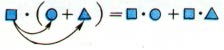
3. А теперь обратим внимание, что наблюдательность нам не помешает при упрощенных вычислениях.
У вас на доске приведен пример, который используется для устного счета
92 * 8 = (90+2) * 8 = 90 * 8 + 2 * 8 = 720 + 16 = 736
49 * 7 = (50-1) * 7 = 50 * 7 - 1 * 7 = 350 - 7 = 743
Пользуясь данным приемом вычислите:
121 * 4
89 * 8
Вопрос: Какое свойство вы должны были вспомнить, чтобы решить более удобным способом числовые выражения?
Вывод: Мы вспомнили распределительное свойство умножения относительно сложения и распределительное свойство умножения относительно вычитания.
К данному свойству мы еще с вами вернемся, а теперь я вам предлагаю немного отвлечься и в парах решить кроссворд.
III Проверка теоретических знаний (раздаточный материал)
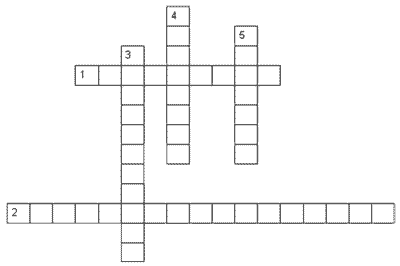
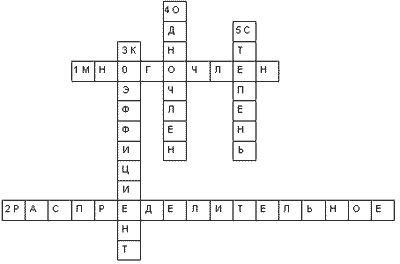
По горизонтали:
1 - Алгебраическая сумма одночленов.
2 - Свойство, при котором произведение числа и суммы чисел равно сумме произведений данного числа и каждого слагаемого.
По вертикали:
3 - Числовой множитель одночлена, записанного в стандартном виде.
4 - Произведение чисел, переменных и их степеней.
5 - У одночлена - сумма показателей всех переменных.
Проверка ответов.
IV. Новая тема.
А теперь, как я обещала, возвратимся к распределительному свойству:
a * (b + c) = a * b +a * c
Используя данное свойство выполните умножения:
а) 8 (а + 5)
б) к (1 - к - 3к2)
в) 2n (b - 2n + 4n2 - 5)
г)3(3в+4а-8ав)
Вопрос:Какое действие вы выполняли в каждом из этих упражнений?
Вопрос: Можно ли утверждать, что в каждом из этих трех упражнений вы выполняли умножение одночлена на многочлен
Работа с учебником, с. 135: Прочитайте правило умножения одночлена на многочлен и подтвердите правильность своих действий.
А теперь обратим внимание еще на одну особенность:
Сравните количество членов многочлена в скобках и после выполнения умножения одночлена на многочлен.
Вопрос: Сформулируйте правило - от чего зависит количество членов в произведении при умножении одночлена на многочлен, необходимое для самоконтроля.
Упражнение на закрепление - №615 (а,б)
Проблемный вопрос: №625 - прочитайте задание и посмотрите рисунок 67 в вашем учебнике (рисунок на доске)
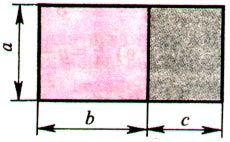
Данное задание интересно потому, что, оказывается, в Древней Греции было принято все алгебраические утверждения выражать в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью (рисунок на доске)

Вопрос: Объясните геометрический смысл формулы:
a (b + c) = ab + bc - это чуть позже, на следующем уроке!!!!
Работа с учебником: Давайте рассмотрим примеры, рассмотренные в пункте вашего учебника, обратим внимание на формулировку заданий и сделаем вывод - где практически можно применить умножение одночлена на многочлен.
Вывод: Умножение одночлена на многочлен можно применить:
- при упрощении выражений;
- при решении уравнений;
- при доказательстве тождеств;
- при решении задач на составление уравнений.
На последующих уроках мы с вами этим и займемся.
V. Применение теоретического материала на практике
1. Самостоятельная работа по карточкам
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Выполните умножение
Выполните умножение
Выполните умножение
Выполните умножение
2х(х2 -7х-3)
-4в2 (5в2 -3в-2)
5а3 (3а3 -а2+а)
3в(а2 -2ав+в)
Проверка
Вариант 1
Вариант 2
Вариант 3
Вариант 4
2хх2 +2х(-7х)+2х(-3)=2х3 -14х2 -6х
-4в2 5в2 -4в2 (-3в)-4в2 (-2)=-20в4 +12в3 +8в2
5а33а3+5а3(-а2)+5а3 а=15а6 -5а5 +5а4
3ва2 +3в(-2ав)+3вв=3а2 в -6ав2 +3в2
(первичный контроль, взаимопроверка).
2. Еще один вариант умножения - умножение в "столбик" (на доске):
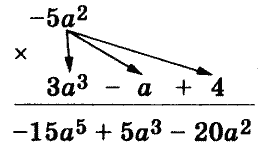
Умножьте одночлен на многочлен:
а) 3n4 (n2 + 2n -4);
б) -2m3 (3m - 2m2 + m3).
3. Дополнительно: № 617
VI. Домашнее задание
п. 27, № 614, 616 (а,б)
VII. Рефлексия:
1. Что нового мы узнали на уроке?
2. Вернемся к нашему эпиграфу
Мы убедились, что наблюдательность дает возможность для применения уже имеющейся информации в новом применении.