Конспект урока+Презентация по математике на тему 'Длина окружности и число пи'

Урок по математике в 6 классе по теме: «Длина окружности и число пи».

Учитель математики
МАОУ СОШ № 2 ст. Павловской
Краснодарского края

Ход урока.

1. Организационный момент. (Проверка готовности к уроку)

2. Проверка домашнего задания по образцу, поменяться тетрадями с соседом. Выставить оценки. Сдать тетради на проверку.

3. В полученных тетрадях: число, классная работа.

4. Устная работа, работа по карточкам.

- Найти неизвестный компонент.

- Округлить.

- Периметр прямоугольника, квадрата.

А что будет являться периметром окружности?

(Сформулировать тему урока «Длина окружности»)

- А как можно измерить, например, длину бордюра круглой клумбы или длину границы цирковой арены? (При помощи веревки, нити, затем распрямить и измерить линейкой)

- А применим ли этот метод для измерения траектории пути спутника? Какая проблема перед нами стала?

- Итак, ребята, какова же цель нашего урока? (найти универсальный способ для нахождения длины окружности и применить наш способ для решения практических задач).

5. Для начала вспомним основные элементы окружности.

Центр

Радиус

Диаметр

Длина окружности

Зависимость диаметра и радиуса.

6. Ребята, еще в далёкой древности было установлено, что также есть зависимость между длиной окружности и её диаметром.

Давайте же и мы попробуем её установить, для этого вы выполните практическую работу, в которой будете использовать способ измерения длины окружности, предложенный вами.

У вас на столах лежат различные круги и как вы говорили, что граница круга - это окружность, то длины окружностей их ограничивающие различны.

Практическая работа. Желтый (2см), Синий (3см), Красный (5см)

1. Проведите диаметр и измерьте его.

2. С помощью нити и линейки измерьте длину окружности.

3. Как вы думаете, чья длина больше? А как определить во сколько раз?

Разделите длину окружности на диаметр и результат округлите до целых.

Для получения наиболее точных результатов, работайте в группах.

После выполнения работы, сделайте вывод: примерно во сколько же раз длина окружности больше своего диаметра.

7. Если вы, ребята, округлили ваш результат, то ваш товарищ, выполнял следующее задание: попробовал выполнить деление С=22 на d=7 до конца. И что же у тебя получилось, ученик записывает свой результат. Да, действительно, получается бесконечная десятичная дробь. К такому выводу пришел древнегреческий ученый Архимед.

8. В 1706 году английский математик Уильямс Джонс для него ввел специальное обозначение 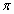-это первая буква слова "периферия", в переводе с греческого "окружность". Необычность и удивительность этого числа в том, что его можно вычислять бесконечно и у него будет бесконечно знаков после запятой. Это, однако, не удерживает математиков от попыток вычислить как можно больше десятичных знаков числа пи. О нём говорят, как о неуловимом числе. Вот как, например, выглядит значение 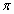с семью знаками после запятой. Для запоминания этих знаков есть стишок:

Нужно только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.

Какие только эксперименты не проводили с числом пи. Один из пользователей ютуба сыграл число пи (Видеоролик 0, 47)

Используя свои выводы и заключения учёных, получили, что для любой окружности С:d=.

И теперь мы можем получить формулу для нахождения длины окружности - это как раз и есть универсальный способ.

Давайте выразим отсюда С.

Получим С=d . Подставив в эту формулу вместо d 2r получим С=2r. Обычно на уроках математики для работы по этим формулам берут или

Т. е. для того, чтобы найти длину окружности нужно знать её диаметр или радиус, а можно наоборот, зная длину окружности найти диаметр, а как? (нужно длину окружности разделить на )

9. А теперь я предлагаю вам устно заполнить таблицы.

10. Решение задач с презентации. № 453- учебник

11. Самоанализ.

12. Домашнее задание.