- Учителю
- Рабочая программа по алгебре и началам математического анализа,11 класс,4 часа
Рабочая программа по алгебре и началам математического анализа,11 класс,4 часа
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по алгебре и началам анализа ориентирована на учащихся 11 классов и реализуется на основе следующих документов:
-
Закона «Об образовании» ст. 32, п. 2 (7).
-
Федеральный компонент государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования (Приказ МО РФ от 05.03.2004 №1089).
-
Базисного учебного плана, утвержденного приказом Министерства образования РФ №1312 от 09.03.2004 г.
-
Учебного плана ОУ.
-
Примерной программы среднего (полного) общего образования по математике и программы для общеобразовательных учреждений по алгебре 10 - 11 классы (к учебному комплекту по алгебре для 10 - 11 классов авторы Ш.А.Алимов и др.), составитель Бурмистрова Т.А.-М.: Просвещение, 2014.
Цель изучения:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
-
приобретение конкретных знаний о пространстве и практически значимых умений, формирование языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося и выпускника, виды контроля, а также компьютерное обеспечение урока.
Задачи изучения:
-
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
-
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
-
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления.
Место предмета:
Рабочая программа рассчитана на 136 часов в год (4 часа в неделю). Рабочая программа обеспечена соответствующим программе учебно-методическим комплексом: Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. учреждений: базовый уровень/Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.-17-е изд.-М.: Просвещение,2011.-464с.
Одна из главных особенностей курса алгебры, представленного в учебниках Ш.А. Алимова и др., заключается в том, что в нем реализуется взаимосвязь принципов научности и доступности, уделяется особое внимание обеспечению прочного усвоения основ математических знаний всеми учащимися. Основной теоретический материал в учебниках излагается с постепенным нарастанием его сложности. Этим достигается необходимая дидактическая и логическая последовательность его построения и возможность научного обоснования основных теоретических положений.
Особенностью курса является также его практическая направленность, которая служит стимулом развития у учащихся интереса к алгебре, основой для формирования осознанных математических навыков и умений.
В рабочую программу внесены следующие изменения: отдельно выделены часы для организации контроля усвоения программы (входной, промежуточный, итоговый); при распределении часов учтена специфика профиля класса.
Формы контроля:
1) контрольная работа,
2) зачёт,
3) самостоятельная работа,
4) проверочная работа,
5) математический диктант,
6) тест.
Календарно-тематический план для 11 класса
(4 часа в неделю, 136 часов в год)СР
КР
ТР
ПР
МД
ЗР
Повторение 10 класса
8
1
Повторение по теме «Действительные числа».
1
3.09
2
Повторение по теме: «Степенная функция».
1
5.09
+
3-4
Повторение по теме: «Показательная функция»
2
6.09
7.09
+
+
5-6
Повторение по теме: «Логарифмическая функция».
2
10.09
12.09
+
+
7
Повторение по теме: «Тригонометрия»
1
13.09
+
8
Входной контроль.
1
14.09
+
Тригонометрические функции
22
9-12
Область определения и множество значений тригонометрических функций.
4
17.09
19.09
20.09
21.09
+
+
13-16
Четность, нечетность, периодичность тригонометрических функций.
4
24.09
26.09
27.09
28.09
+
+
17-20
Свойства функции y= cosx и ее график.
4
1.10
3.10
4.10
5.10
+
+
21-24
Свойства функции y= sinx и ее график.
4
8.10
10.10
11.10
12.10
+
+
25-27
Свойства функции y= tgx и ее график.
3
15.10
17.10
18.10
+
+
28
Обратные тригонометрические функции.
1
19.10
+
29
Урок обобщения и систематизации знаний.
1
22.10
+
30
Контрольная работа №1 по теме: «Тригонометрические функции»
1
24.10
+
Производная и ее геометрический смысл.
24
31-34
Производная.
4
24.10
26.10
7.11
8.11
+
+
35-37
Производная степенной функции.
3
9.11
12.11
14.11
+
+
38-41
Правила дифференцирования.
4
15.11
16.11
19.11
21.11
+
+
42-46
Производные некоторых элементарных функций.
5
22.11
23.11
26.11
28.11
29.11
+
+
47-51
Геометрический смысл производной.
5
30.11
3.12
5.12
6.12
7.12
+
+
52-53
Урок обобщения и систематизации знаний.
2
10.12
12.12
+
+
54
Контрольная работа №2 по теме: «Производная».
1
13.12
+
Применение производной к исследованию функций.
21
55-58
Возрастание и убывание функции.
4
14.12
17.12
19.12
20.12
+
+
59-62
Экстремумы функции.
4
21.12
24.12
26.12
27.12
+
+
63-66
Применение производной к построению графиков функций.
4
28.12
9.01
10.01
11.01
+
+
67-72
Наибольшее и наименьшее значения функции.
6
14.01
16.01
17.01
18.01
21.01
23.01
+
+
73
Выпуклость графика функции, точка перегиба.
1
24.01
+
74
Урок обобщения и систематизации знаний.
1
25.01
+
75
Контрольная работа №3 по теме: «Применение производной».
1
28.01
+
Интеграл.
17
76-77
Первообразная.
2
30.01
31.01
+
78-81
Правила нахождения первообразных.
4
1.02
4.02
6.02
7.02
+
82-85
Площадь криволинейной трапеции и интеграл.
4
8.02
11.02
13.02
14.02
+
86-87
Вычисление интегралов.
2
15.02
18.02
+
+
88-89
Вычисление площадей с помощью интегралов.
2
20.02
21.02
+
90
Применение производной и интеграла к решению практических задач.
1
22.02
+
91
Урок обобщения и систематизации знаний.
1
25.02
+
92
Контрольная работа № 4 по теме: «Интеграл».
1
27.02
+
Комбинаторика.
13
93
Правило произведения.
1
28.02
+
94-95
Перестановки.
2
1.03
4.03
+
+
96-98
Размещения.
3
6.03
7.03
9.03
+
+
99-102
Сочетания и их свойства.
4
11.03
13.03
14.03
15.03
103
Бином Ньютона.
1
18.03
+
104
Урок обобщения и систематизации знаний.
1
20.03
+
105
Контрольная работа №5 по теме: «Комбинаторка».
1
21.03
+
Элементы теории вероятностей.
9
106
События.
1
22.03
+
107
Комбинация событий. Противоположное событие.
1
3.04
+
108-109
Вероятность события.
2
4.04
5.04
+
+
110
Сложение вероятностей.
1
8.04
+
111
Независимые события. Умножение вероятностей.
1
10.04
+
112
Статистическая вероятность.
1
11.04
+
113
Урок обобщения и систематизации знаний.
1
12.04
+
114
Контрольная работа №6 по теме: «Элементы теории вероятностей»
1
15.04
+
Статистика.
5
115
Случайные величины.
1
17.04
+
116
Центральные тенденции.
1
18.04
+
117
Меры разброса.
1
19.04
+
118
Урок обобщения и систематизации знаний.
1
22.04
+
119
Контрольная работа №7 по теме: «Статистика».
1
24.04
+
Итоговой повторение, подготовка к ЕГЭ
17
120-121
Повторение по теме: «Числа и вычисления».
2
25.04
26.04
+
+
122-123
Повторение по теме: «Преобразование выражений».
2
29.04
2.05
+
+
124-127
Повторение по теме: «Уравнения и неравенства».
4
3.05
6.05
8.05
10.05
+
+
+
128-131
Повторение по теме: «Функции и графики».
4
13.05
15.05
16.05
17.05
+
+
+
132-133
Итоговая контрольная работа
2
18.05
18.05
+
134-136
Повторение по теме: «Текстовые задачи».
3
20.05
22.05
23.05
+
+
Содержание учебного предмета
Повторение 10 класса.
8
Действительные числа. Степенная функция. Показательная функция. Логарифмическая функция. Тригонометрия.
2
Тригонометрические функции.
22
Область определения и множество значений тригонометрических функций. Четность, нечетность, периодичность тригонометрических функций. Свойства функций y=cosx, y=sinx, y=tgx и их графики.
3
Производная и ее геометрический смысл.
24
Производная. Производная степенной функции. Правила дифференцирования. Производные некоторых элементарных функций. Геометрический смысл производной.
4
Применение производной к исследованию функций.
21
Возрастание и убывание функции. Экстремумы функции. Применение производной к построению графиков функции. Наибольшее и наименьшее значения функции. Выпуклость графика функции, точка перегиба.
5
Интеграл.
17
Первообразная. Правила нахождения первообразных. Площадь криволинейной трапеции и интеграл. Вычисление интегралов. Вычисление площадей с помощью интегралов. Применение производной и интеграла к решению практических задач.
6
Комбинаторика.
13
Правило произведения. Перестановки. Размещения. Сочетания и их свойства. Бином Ньютона.
7
Элементы теории вероятностей.
9
События. Комбинация событий. Противоположное событие. Вероятность события. Сложение вероятностей. Независимые события. Умножение вероятностей. Статистическая вероятность.
8
Статистика.
5
Случайные величины. Центральные тенденции. Меры разброса.
9
Итоговое повторение, подготовка к ЕГЭ.
17
ИТОГО
136
Требования к уровню подготовки выпускников 11 классов
В результате изучения математики на базовом уровне ученик должен:
знать/понимать
- значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
- значение практики и вопросов, возникающих в самой математике для формирования и развития понятия числа, создания математического анализа, возникновения и развития геометрии;
- универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
- вероятностный характер различных процессов окружающего мира;
Алгебра
уметь
- выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимость вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
- проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, корни, логарифмы и тригонометрические функции;
- вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- практических расчетов по формулам, включая формулы, содержащие степени, корни, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
- определять значение функции по значению аргумента при различных способах задания функции;
- строить графики изученных функций;
- описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
- решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
Начала математического анализа
уметь
- вычислять производные и первообразные элементарных функций, используя справочные материалы;
- исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функции, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
- вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- решения прикладных задач, в том числе социально-экономических и физических, на наибольшее и наименьшее значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь
-решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
- составлять уравнения и неравенства по условию задачи;
- использовать для приближенного решения уравнений и неравенств графический метод;
- изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- построения и исследования простейших математических моделей;
Элементы комбинаторики, статистики и теории вероятностей
уметь
- решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
- вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- анализа реальных числовых данных, представленных в виде диаграмм, графиков;
- анализа информации статистического характера.
Требования к уровню подготовки учащихся
Модуль 1. «Повторение курса алгебры и начал анализа
10 класса»
Раздел математики. Сквозная линия
-
Числа и вычисления
-
Функции
Обязательный минимум содержания образовательной области математика
-
Действительные числа.
-
Степенная функция, ее свойства и график.
-
Показательная функция, ее свойства и график.
-
Логарифмическая функция, ее свойства и график.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
-
Уметь решать несложные алгебраические, иррациональные, показательные, логарифмические, тригонометрические уравнения, неравенства и их системы.
-
Знать свойства степенной, показательной, логарифмической функций и уметь строить их графики.
Уровень возможной подготовки обучающегося
-
Уметь решать алгебраические, иррациональные, показательные, логарифмические, тригонометрические уравнения, неравенства и их системы, применяя различные методы их решений.
-
Знать свойства степенной, показательной, логарифмической функций и уметь строить их графики. Уметь применять свойства функций при решении различных задач.
Модуль 2. «Тригонометрические функции»
Раздел математики. Сквозная линия
-
Функции
Обязательный минимум содержания образовательной области математика
-
Область определения тригонометрических функций.
-
Множество значений тригонометрических функций.
-
Четность, нечетность, периодичность тригонометрических функций.
-
Свойства функций у=cosx, y=sinx.
-
Графики функций у=cos x, y=sinx.
-
Свойства функции y=tgx
-
График функции y=tgx.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
-
Научиться находить область определения тригонометрических функций.
-
Научиться находить множество значений тригонометрических функций.
-
Научиться определять четность, нечетность, периодичность тригонометрических функций.
-
Знать свойства тригонометрических функций
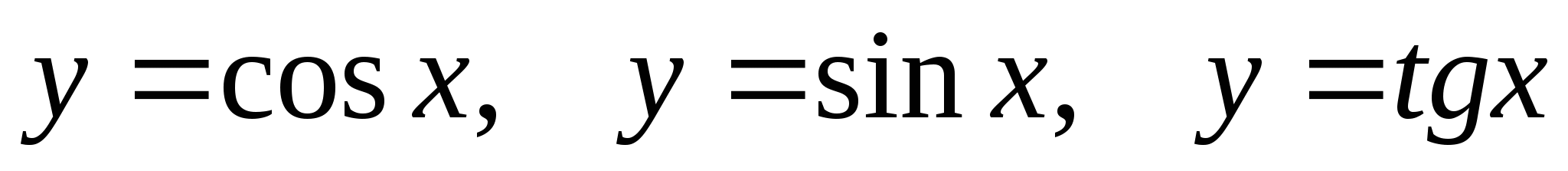и уметь строить их графики.
Уровень возможной подготовки обучающегося
-
Научиться находить область определения и множество значений тригонометрических функций в более сложных случаях.
-
Научиться определять четность, нечетность, периодичность тригонометрических функций в более сложных случаях.
-
Знать свойства тригонометрических функций
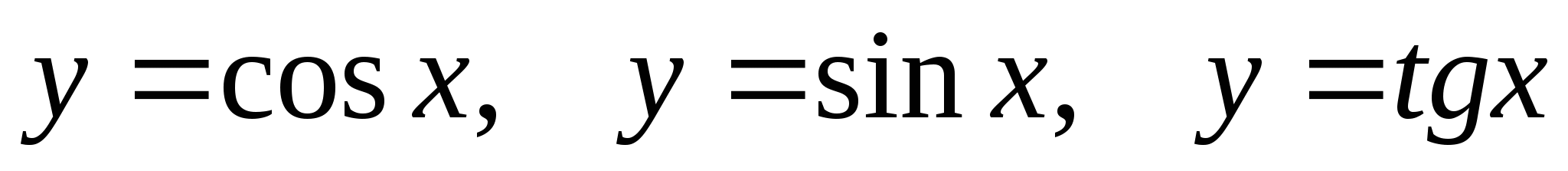и уметь строить их графики. Уметь выполнять преобразования
графиков.
-
описывать по графику и в простейших случаях по формуле поведение и свойства тригонометрических функций, находить по графику функции наибольшие и наименьшие значения;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
-
Научится определять свойства обратных тригонометрических функций и выполнять эскизы их графиков, используя эти свойства.
Модуль 3. «Производная и ее геометрический смысл»
Раздел математики. Сквозная линия
-
Функции
Обязательный минимум содержания образовательной области математика
-
Понятие о пределе и непрерывности функции.
-
Производная. Физический смысл производной.
-
Таблица производных
-
Производная суммы, произведения и частного двух функций.
-
Геометрический смысл производной.
-
Уравнение касательной.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
-
Понимать механический смысл производной.
-
Находить производные элементарных функций, пользуясь таблицей производных.
-
Находить производные элементарных функций, пользуясь правилами дифференцирования.
-
Понимать геометрический смысл производной.
Уровень возможной подготовки обучающегося
-
Овладеть понятием производной (возможно на наглядно-
-
интуитивном уровне). Усвоить механический смысл производной
-
Освоить технику дифференцирования.
-
Усвоить геометрический смысл производной.
Модуль 4. «Применение производной к исследованию функций»
Раздел математики. Сквозная линия
Функции
Обязательный минимум содержания образовательной области математика
-
Исследование свойств функции с помощью производной.
-
Нахождение промежутков монотонности.
-
Нахождение экстремумов функции
-
Построение графиков функций.
-
Нахождение наибольших и наименьших значений.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
-
Применять производные для исследования функций на монотонность в несложных случаях.
-
Применять производные для исследования функций на экстремумы в несложных случаях.
-
Применять производные для исследования функций и построения их графиков в несложных случаях.
-
Применять производные для нахождения наибольших и наименьших значений функции
Уровень возможной подготовки обучающегося
-
Научиться применять дифференциальное исчисление для исследования элементарных и сложных функций и построения их графиков.
-
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Модуль 5. «Интеграл»
Раздел математики. Сквозная линия
-
Функции
Обязательный минимум содержания образовательной области математика
-
Первообразная.
-
Правила нахождения первообразных
-
Площадь криволинейной трапеции.
-
Вычисление интегралов.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
-
Научиться находить первообразные, пользуясь таблицей первообразных.
-
Научиться вычислять интегралы в простых случаях.
-
Научиться находить площадь криволинейной трапеции.
Уровень возможной подготовки обучающегося
-
Освоить технику нахождения первообразных.
-
Усвоить геометрический смысл интеграла.
-
Освоить технику вычисления интегралов.
-
Научиться находить площади фигур в более сложных случаях.
Модуль 6. «Элементы теории вероятностей»
Раздел математики. Сквозная линия
-
Числа и вычисления.
-
Множества и комбинаторика.
-
Статистика.
-
Вероятность.
Обязательный минимум содержания образовательной области математика
-
Перестановки, сочетания и размещения в комбинаторике.
-
Случайные события и их вероятности.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
-
Уметь решать комбинаторные задачи.
-
Уметь находить вероятности случайных событий в простейших случаях.
Уровень возможной подготовки обучающегося
-
Уметь находить частоту события, используя собственные наблюдения и готовые статистические данные.
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения учебных и практических задач, требующих систематического перебора вариантов.
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией.
Модуль 7. «Итоговое повторение курса
алгебры и начал анализа, подготовка к ЕГЭ»
Раздел математики. Сквозная линия
-
Вычисления и преобразования
-
Уравнения и неравенства
-
Функции
-
Множества и комбинаторика. Статистика. Вероятность.
Обязательный минимум содержания образовательной области математика
-
Корень степени n.
-
Степень с рациональным показателем.
-
Логарифм.
-
Синус, косинус, тангенс, котангенс. Прогрессии.
-
Общие приемы решения уравнений. Решение уравнений. Системы уравнений с двумя переменными. Неравенства с одной переменной.
-
Область определения функции.
-
Область значений функции.
-
Периодичность. Четность (нечетность). Возрастание (убывание).
-
Экстремумы. Наибольшее (наименьшее) значение.
-
Графики функций.
-
Производная.
-
Исследование функции с помощью производной.
-
Первообразная. Интеграл.
-
Площадь криволинейной трапеции.
-
Статистическая обработка данных.
-
Решение комбинаторных задач.
-
Случайные события и их вероятности.
Уровень обязательной подготовки обучающегося
Уметь:
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций;
-
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
-
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
-
вычислять производные и первообразные элементарных функций, используя справочные материалы;
-
исследовать в простейших случаях функции на монотонность, находить наибольшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
-
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы.
Уровень возможной подготовки обучающегося
-
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
-
вычислять площади с использованием первообразной;
-
использовать для приближенного решения уравнений и неравенств графический метод;
-
изображать на координатной плоскости множества решений простейших уравнений и их систем.
-
строить графики изученных функций;
-
описывать по графику и по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
-
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
-
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
-
построения и исследования простейших математических моделей.
Критерии и нормы оценки знаний, умений, навыков обучающихся применительно к различным формам контроля знаний
-
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
-
работа выполнена полностью;
-
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
-
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
-
допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
-
допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
-
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
-
Оценка устных ответов обучающихся.
Ответ оценивается отметкой «5», если ученик:
-
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником
-
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
-
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
-
отвечал самостоятельно, без наводящих вопросов учителя;
-
возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя
Ответ оценивается отметкой «4»,если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
-
допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
-
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
-
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
-
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
-
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях
-
не раскрыто основное содержание учебного материала;
-
обнаружено незнание учеником большей или наиболее важной части учебного материала;
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
-
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу
-
Общая классификация ошибок.
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
-
Грубыми считаются ошибки:
-
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
-
незнание наименований единиц измерения;
-
неумение выделить в ответе главное;
-
неумение применять знания, алгоритмы для решения задач;
-
неумение делать выводы и обобщения;
-
неумение читать и строить графики;
-
неумение пользоваться первоисточниками, учебником и справочниками;
-
потеря корня или сохранение постороннего корня;
-
отбрасывание без объяснений одного из них;
-
равнозначные им ошибки;
-
вычислительные ошибки, если они не являются опиской;
-
логические ошибки.
-
К негрубым ошибкам следует отнести
-
-
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
-
неточность графика;
-
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
-
нерациональные методы работы со справочной и другой литературой;
-
неумение решать задачи, выполнять задания в общем виде.
-
-
Недочетами являются:
-
-
нерациональные приемы вычислений и преобразований;
-
небрежное выполнение записей, чертежей, схем, графиков.
Материально-техническое обеспечение
-
Компьютер с мультимедиапроектором и экраном.
-
Алгебра и начала математического анализа.10-11 классы: учеб. для общеобразоват. учреждений: базовый уровень/Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.-17-е изд.-М.: Просвещение,2011.-464с.
-
Дидактические материалы для 10-11 классов. М.В.Шабунин, М.В. Ткачева. Издательство: Просвещение, 2009.-144с.
-
Математика. Тематические тесты. Часть I.(базовый уровень). Подготовка к ЕГЭ-2010. 10-11 класс/Под редакцией Ф.Ф.Лысенко, С.Ю. Кулабухова. -Ростов-на-Дону: Легион, 2010. 272с.
-
Математика. Тематические тесты. Часть II. Подготовка к ЕГЭ-2010. 10-11 класс/под редакцией Ф.Ф.Лысенко.- Ростов-на-Дону: Легион, 2009.-176с.
-
Математика. Подготовка к ЕГЭ-2010. Учебно-тренировочные тесты/ Под редакцией Ф.Ф.Лысенко, С.Ю. Кулабухова. Ростов-на-Дону: Легион-М.2010.-144с.
-
Математика. Подготовка к ЕГЭ-2010. Тематические тесты: геометрия, тестовые задачи. Учебно-методическое пособие/Под редакцией Ф.Ф.Лысенко.-Ростов н/Д: Легион-М,2009.-96с
-
Математика. Подготовка к ЕГЭ-2013: учебно-методическое пособие /Под редакцией Ф.Ф.Лысенко, С.Ю.Кулабухова.-Ростов-на-Дону: Легион, 2012.-416с
-
Единый государственный экзамен 2012. Математика. Универсальные материалы для подготовки учащихся/ ФИПИ- М.: Интеллект-Центр, 2012.-144с.
-
Математика: 50 типовых вариантов экзаменационных работ/авт.сост. А.П.Власова, Н.В.Евсеева, Н.И.Латанова и др.-М.: АСТ: Астрель; Владимир: ВКТ, 2011.-318с.
-
Панферов В.С., Сергеев И.Н. Отличник ЕГЭ. Математика. Решение сложных задач ФИПИ-М.: Интеллект-Центр, 2010.-80с
-
Электронный учебник-справочник 7-11 класс. Алгебра. «Кордис @Медиа» 2000г
-
Учебное электронное издание. Математика 5-11 класс. Практикум. Дрофа 2004г
-
Учебное электронное издание Математика 5-11 классы. Практикум 2004г. Под редакцией Дубровского В.Н.
-
Учебное электронное издание. Интерактивная математика 5-9 классы. Дрофа 2002г.
-
http://www.1september.ru
-
http://www.edu.ru</</p>
