Учителю
Конспекты уроков по алгебре в 9 классе по теме «Целое уравнение и его корни»

Конспекты уроков по алгебре в 9 классе по теме «Целое уравнение и его корни»

Автор публикации: Чудненко Л.В.

Дата публикации: 01.06.2015

Краткое описание: Уважаемые коллеги! Предлагаю Вам 2 последовательных урока алгебры в 9 классе по теме "Целое уравнение и его корни. При реализации 1 урока выполняются следующие цели:1.образовательные: обобщить и углубить сведения об уравнениях;ввести понятие целого уравнения и его степе

предварительный просмотр материала

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №14

села Орловки Буденновского района»

Конспекты уроков по алгебре в 9 классе

по теме «Целое уравнение и его корни»

Подготовил:

Чудненко Л.В.

учитель математики

2012-2013 уч. год

УРОК № 1

Тема урока: «Целое уравнение и его корни».

Цели:

образовательные:
- обобщить и углубить сведения об уравнениях;
- ввести понятие целого уравнения и его степени, его корней;
- рассмотреть способ решения целого уравнения с помощью разложения на множители;
развивающие:
- развитие математического и общего кругозора, логического мышления, умение анализировать, делать вывод;
воспитательные:
- воспитывать самостоятельность, четкость и аккуратность в действиях.

Класс: 9

Учебник: Алгебра. 9 класс: учебник для общеобразовательных учреждений/ [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А. Теляковского.- 16-е изд. - М.: Просвещение, 2010

Оборудование: компьютер с проектором, презентация «Целые уравнения»

Ход урока:

Организационный момент.

Сообщение темы урока, цели.

Сегодня мы познакомимся с новым видом уравнений - это целые уравнения. Научимся их решать.

Запишем в тетради число, классная работа и тему урока: «Целое уравнение, его корни».

2.Актуализация опорных знаний.

Решите уравнение:

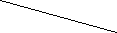
Ответы: 1)х = -2; 2) х =1/2; 3) х = -4, +4; 4) х = -8; 5) корней нет; 6) х = 0

- определите степень каждого многочлена:

38х⁵+8-3y 7y-76х⁶ 9х-76х²+12

3.Формирование новых понятий.

Беседа с учениками:

Что такое уравнение? (равенство, содержащее неизвестное число)
Какие виды уравнений вы знаете? (линейные, квадратные)
Приведите примеры линейных уравнений, квадратных.

-Сколько корней может иметь линейное уравнение?) (один, множество и ни одного корня)

1)5х=0 2) 0y=3 в)6х-2=4

-Какое из этих уравнений имеет один корень? (не имеет корней, имеет множество решений)

-Сколько корней может иметь квадратное уравнение?

Отчего зависит количество корней? (от дискриминанта)

-В каком случае квадратное уравнение имеет 2 корня?( Д>0)

- В каком случае квадратное уравнение имеет 1 корень? (Д=0)

- В каком случае квадратное уравнение не имеет корней? ( Д0)

-Дадим определение данному типу уравнений, но для начала вспомним, какие выражения называются целыми? (Целые выражения это такие, которые состоят из умножения, сложения, вычитания выражений содержащих переменную, а также деления на число)

Целое уравнение - это уравнение левая и правая часть, которого является целым выражением. (читают вслух).

Приведем примеры целых уравнений: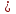

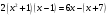
Приведите и запишите свой пример целого уравнения (попросить нескольких учеников записать на доске свои уравнения)

-Из рассмотренных линейных и квадратных уравнений, мы видим, что количество корней не больше его степени.

-Как вы думаете, можно ли не решая уравнения, определить количество его корней? (возможные ответы детей)

-Познакомимся с правилом определения степени целого уравнения?

Если уравнение с одной переменной записано в виде Р(х)=0, где Р(х)- многочлен стандартного вида, то степень этого многочлена называют степенью уравнения. Степенью произвольного целого уравнения называют степень равносильного ему уравнения вида Р(х)=0, где Р(х)- многочлен стандартного вида.

Уравнение n^ой степени имеет не более n корней.

Например: 1)4х⁴-5х²+1=0; 2)(х-2)(х+2)=0

-Являются ли эти уравнения целыми?

-Записаны ли эти уравнения в виде Р(х)=0?

-Степень какого уравнения можно определить сразу? (1)

-Сколько корней может иметь это уравнение?

-Что нужно сделать со вторым уравнением, чтобы определить его степень?

( заменить ему равносильным и записать в виде Р(х)=0)

- Замените это уравнение ему равносильным и запишите в виде Р(х)=0

(х²-4=0)

-Определите степень полученного уравнения

- Сколько корней может иметь 2 уравнение?

Целое уравнение можно решить несколькими способами:

способы решения целых уравнений

разложение на множители графический введение новой

переменной

(Записывают схему в тетрадь)

Сегодня мы рассмотрим один из них: разложение на множители на примере следующего уравнения: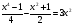 ( на доске объясняет учитель , ученики записывают в тетрадь решение уравнения)

-Как называется способ разложения на множители, с помощью которого можно левую часть уравнения разложить на множители? (способ группировки). Разложим левую часть уравнения на множители, а для этого сгруппируем слагаемые, стоящие в левой части уравнения.

-Когда произведение множителей равно нулю? (когда хотя бы один из множителей равен нулю). Приравняем к нулю каждый множитель уравнения.

Решим полученные уравнения

-Сколько корней мы получили? (запись в тетради)

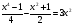
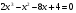
Ответ:-2;1⁄2; 2.

4.Формирование умений и навыков. Практическая часть.

работа по учебнику №265( устно а-в, г-д- запись в тетради)

Какова степень уравнения и сколько корней имеет каждое из уравнений:

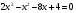
Ответы: а) 5, б) 6, в) 5, г) 2, д) 1, е) 1

№ 266 (решение у доски с объяснением)

Решите уравнение:

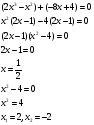
Ответ:-2

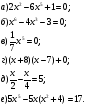
Ответ:3⁄15;-3⁄15.

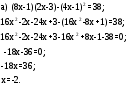
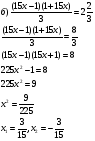
Ответ:-1⁄2;1⁄2.

№ 268 (решение у доски с объяснением)

Докажите, что уравнение 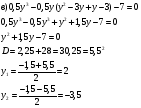не имеет корней:

Запишем уравнение в виде 5x⁶+6x⁴+x²=-4.

В левую часть уравнения х входит только в четной степени, следовательно, число неотрицательное, а в правой части - число отрицательное, значит, уравнение корней не имеет.

5.Итог урока:

Закрепление теоретического материала:

Какое уравнение с одной переменной называется целым? Приведите пример.
Как найти степень целого уравнения? Сколько корней имеет уравнение с одной переменной первой, второй степени?

6.Рефлексия

- Дайте оценку своей работе и прикрепите цветной магнит на доске.

1)Отлично, вопросов нет …

2)Хорошо, но могу лучше …

Пока испытываю трудности …

7.Домашнее задание:

п.12(с.72-73)№267,№269,№270.

УРОК № 2

Тема урока: «Целое уравнение и его корни».

Цели:

образовательные:

дать понятие биквадратного уравнения и способа его решения;

развивать умение определять степень целого уравнения, его корни;
рассмотреть способ решения целого уравнения третьей степени с помощью введения новой переменной;

развивающие:

развивать умение самостоятельно выбирать рациональный способ решения целого уравнения;
развитие математического и общего кругозора, логического мышления; умения ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления; развивать внимательность, собранность и аккуратность.

воспитательные:

наблюдательность;

воспитывать самостоятельность, четкость и аккуратность в действиях.

4.социально-психологические:

развитие способности проявлять себя в различных социальных ролях- исполнителя, эксперта, исследователя, помощника; обучение культуре общения в коллективе.

Класс: 9

Оборудование: компьютер с проектором, презентация «Целые уравнения»

Ход урока:

1.Организационный момент.

Сообщение темы урока, цели.

-Сегодня на уроке мы продолжим работу по теме» Целое уравнение и его корни», познакомимся с новым способом решения целых уравнений. В тетрадях записываем число, классная работа, тему урока

2.Актуализация опорных знаний.

-Какое уравнение называется целым?

-Являются ли эти уравнения целыми? Почему? (т.к их левые и правые части являются целыми выражениями, то эти уравнения-целые)

-Найдите корни данных уравнений и определите их степень.

(х-5)(х+1)(3х-6) =0 ( корни :-1;2;5; 3степень)

х(х²-4)=0 (корни:-2;0;2; 3 степень)

(х²+49)(х+3)=0 (корень -3; 3 степень)

(2х-4)(х³-1)=0 (корни:1;2; 4 степень)

(х³+1)(х²-25)=0 (корни:-5;-1;5; 5 степень)

-Какими способами можно решать целые уравнения?

-В чём заключается сущность способа разложения на множители?

-Как вы думаете, всегда ли возможно решить целое уравнение этим способом?

3.Изучение нового материала

1)решим уравнение (х²-5х+4)(х²-5х+6)=120 (1)

-Как будем решать это уравнение?

(раскроем скобки, перенесём все члены уравнения в левую часть, приведём подобные)

запись в тетрадях и на доске х⁴-10х³+6х^2-5х³+25х²-30х+4х²-20х+24-120=0

х⁴-10х³+35х²-50х-96=0

-Знаем ли мы способ решения уравнения четвёртой степени? (ответы детей)

-Уравнения, степень которых выше двух, иногда удаётся решить, введя новую переменную

-Что особенного в уравнении (1)?

-В левой части уравнения (1) переменная х входит только в выражение х²-5х.

-Сколько раз повторяется это выражение? (дважды)

Это позволяет решить это уравнение с помощью введения новой переменной

(учитель объясняет и записывает решение на доске, а дети в тетради)

(х²-5х+4)(х²-5х+6)=120

1.Введём новую переменную y=х²-5х.

2.Получим уравнение (у+4)(у+6)=120.

3.Решим данное уравнение: у²+6у+4у+24-120=0

у²+10у-96=0

Д=10²-4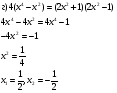1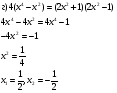(-96)=100+384=484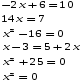0, 2 корня

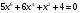
у=

у₁= 6 у₂=-16

4.Вернёмся к замене:

х²-5х=6 и х²-5х=-16

х²-5х-6=0 х²-5х+16=0

Д=(-5)²-4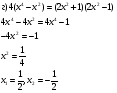1(-6)=49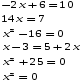0, Д=(-5)²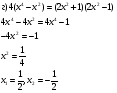-4116=-41,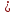

2 корня нет корней

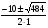
х=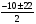

х₁=6 х₂=-1

Ответ:-1;6.

-Составим алгоритм решения уравнений, приводимых к квадратным:

Алгоритм решения уравнений, приводимых к квадратным:

Ввести замену переменной.
Составить квадратное уравнение с новой переменной и решить его
Вернуться к замене переменной.
Решить получившиеся уравнения.
Сделать вывод о количестве корней.
Записать ответ.

2)рассмотрим уравнение 9х⁴-10х²+1=0

-Определите степень этого уравнения

-Можно ли решить это уравнение уже изученными способами?

-Для решения уравнений четвёртой степени, имеющих вид ах⁴+bх²+с=0 используют метод введения новой переменной. Дадим определение уравнений этого вида.

Уравнения вида ах⁴+bх²+с=0 , где а0, являющиеся квадратными относительно х², называют биквадратными.

Решим уравнение 9х⁴-10х²+1=0

1.Введём новую переменную: у=х².

2. Получим уравнение: 9у²-10у+1=0

Далее учащиеся самостоятельно решают полученное уравнение в тетрадях , 1 ученик у доски для последующей проверки)

Д=(-10)²-4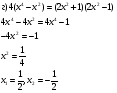9100-36=64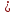

у =

у=

у₁=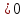 или у₂=1

Вернёмся к замене: х²= 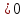или х²=1

х₁=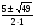;х₂=-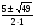 х₃=1; х₄=-1.

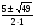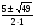Ответ: -; -1; ;1.

4.Закрепление изученного материала:

работа по учебнику№277(а),№278(а) (используя индивидуальные карточки и с алгоритмом решения уравнений, приводимых к квадратным)

№277(а)

(х²+3)²-11(х²+3)+28=0. Пусть х²+3=у

у²-11у+28=0

Д=(-11)²-4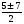

у=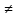

у₁=7 у₂=4

Вернёмся к замене: х²+3=7 или х²+3=4

х²=4 х²=1

х₁=2; х₂=-2; х₃=1; х₄=-1.

Ответ: -2; -1; 1; 2.

№278(а)

х⁴-5х²-36=0. Пусть х²=у.

Тогда у²-5у-36=0

Д=(-5)²-

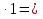
у=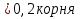

у₁=9 у₂=-4

Вернёмся к замене: х²=9 или х²=-4

х₁₌3; х₂=-3 корней нет

Ответ:-3; 3.

5.Подведение итогов

-Дайте определение биквадратного уравнения. Объясните, как решают биквадратные уравнения?

-Уравнения каких степеней мы рассмотрели?

Для курса высшей математики известны формулы для нахождения корней третьей и четвёртой степени, однако они сложны и громоздки и не имеют практического применения. Для уравнений пятой и более высоких степеней формул не существует. Это было доказано в 19 веке Нильсом Абелем и Эваристом Галуа.

6. Рефлексия

анкета для учащихся (смотри приложение)

7.Домашнее задание

составить и решить уравнения высших степеней на данные методы решения (по 2 уравнения)

ПРИЛОЖЕНИЕ

УВАЖАЕМЫЕ РЕБЯТА!

Просим Вас ответить на данные вопросы.

Ваше отношение к уроку:
1. Мне понравилось заниматься;
2. Мне было трудно;
3. Математика точно не для меня;
4. Другое ________________________________________________
  - С каким настроением Вы шли на данный урок? (поставьте «галочку» около соответствующего знака)
    - _______
      - _______
        
        _______

Считаете ли Вы, что цели данного урока достигнуты?
1. да;
2. нет.
Усвоили ли Вы главное в изученной теме?
1. да;
2. нет.
Научились ли Вы решать уравнения по теме урока?
1. да;
2. нет.
  - Поставьте «галочку» около соответствующего знака, который отвечает Вашему настроению по окончании урока:
    - _______
      - _______
        
        _______

Спасибо за ответы.

⇧

⇩

скачать материал