Методическое пособие для самостоятельной работы по разделу «Степенная, показательная и логарифмическая функции». СПО 2 курс

Департамент образования, науки и молодежной политики Воронежской области

государственное бюджетное профессиональное образовательное учреждение Воронежской области

«Воронежский политехнический техникум»

(ГБПОУ ВО «ВПТ»)

РАССМОТРЕНО

на заседании цикловой комиссии

математических, естественно-научных дисциплин

Протокол от «___»_______ 201___ г.

№ ___

УТВЕРЖДАЮ

Заместитель директора по учебной

работе

_________ Т.И. Агафонова

«____»____________ 20_____ г.

Методическое пособие для самостоятельной работы по разделу «Степенная, показательная и логарифмическая функции».

по дисциплине Математика

19.02.10 Технология продукции общественного питания

23.02.03 Техническое обслуживание и ремонт автомобильного транспорта

Разработал: ______преподаватель Л. Н. Ткаченко

Председатель

цикловой комиссии: _________ В.В. Солманова

2016 г.

Пояснительная записка

В условиях реализации государственных образовательных стандартов нового поколения внеаудиторная нагрузка является обязательной формой работы для каждого студента и подлежит контролю и оцениванию со стороны преподавателя. Новизна требования образовательных стандартов для студентов состоит в том, чтобы сформировать желание и умение учиться и самосовершенствоваться, развиваться всю жизнь, работать в команде. В основе самостоятельной работы студента должен лежать деятельностный подход. Он заключается в том, что бы учащиеся получали не только готовые знания, но и добывали их сами, осознавая при этом содержание и формы своей учебной деятельности. Данные подходы развивают творческий потенциал личности и способствуют приобретению собственного опыта деятельности, способности адекватного принятия решения в условиях выбора. Вам будут предложены разнообразные формы работы:

• работа с источниками информации, с современными средствами коммуникации;

• решение познавательных и практических задач, отражающих типичные ситуации;

Методичка содержит основные вопросы теории по изучаемому разделу математики, примеры решения задач, контрольные вопросы по данному разделу для систематизации материала, а также задачи для самостоятельного решения.

</ Степенная, показательная и логарифмическая функции

1. Понятие функции, область определения и множество значений, основные свойства функции.

Определение. Переменная у называется функцией переменной х, если каждому допустимому значению х соответствует определенное значение у.

Определение. Областью определения функции называется множество всех действительных значений аргумента, при которых она может иметь действительное значение. Обозначается область определения функции .

Определение. Множеством значений функции называется множество всех действительных значений , которые она может принимать. Обозначается множество значений функции .

Чтобы найти область определения функции нужно из множества действительных чисел исключить те, при которых выражение, задающее функцию, теряет смысл.

Примеры решения.

Пример 1. Найти область определения функций: .

Решение.

Областью определения многочлена является общая часть области определения каждого слагаемого. Для первого слагаемого , что следует из определения арифметического квадратного корня. Для второго слагаемого ограничений нет, т. е. . Следовательно, область определения функции служит промежуток .

Ответ: .

Пример 2. Найти область определения функций: .

Решение.

Степенной многочлен не имеет ограничений в значении переменной, следовательно, .

Пример 3. Найти область определения функций: .

Решение.

Данная функция определена при всех значениях х, удовлетворяющих неравенству . Таким образом, область определения найдем из совокупности систем: . Следовательно, область определения состоит из двух промежутков: .

Ответ: .

Пример 4. Найти область определения функций: .

Решение.

Данная функция определена при всех значениях х, удовлетворяющих условиям: и . Таким образом, область определения найдем из совокупности . Следовательно, область определения состоит из трех промежутков: .

Ответ: .

Пример 5. Найти область определения функций: .

Решение.

Данная функция определена при всех значениях х, удовлетворяющих условию: , т. к. в числителе дроби стоит степенной многочлен, и его область определения ограничений не имеет. Решим неравенство: . Следовательно, область определения состоит из двух промежутков: .

Ответ: .

2.Четные и нечетные функции

Определение. Функция называется четной, если при всех значениях х из области определения этой функции при изменении знака аргумента на противоположный значение функции не изменяется, т. е. .

График четной функции симметричен относительно оси ординат (оси Оу).

Определение. Функция называется нечетной, если при всех значениях х из области определения этой функции при изменении знака аргумента на противоположный значение функции изменяется только по знаку, т. е. .

График нечетной функции симметричен относительно начала координат.

Если функция не обладает свойством четности или нечетности, она не является ни четной, ни нечетной и называется функцией общего вида.

Примеры решения.

Пример 1. Исследовать на четность и нечетность функцию , определенную на всей числовой оси.

Решение. Подставим на место аргумента : , следовательно, данная функция четная.

Пример 2. Исследовать на четность и нечетность функцию , определенную на всей числовой оси.

Решение. Подставим на место аргумента : , следовательно, данная функция нечетная.

Пример 3. Исследовать на четность и нечетность функцию , определенную на всей числовой оси.

Решение. Подставим на место аргумента :

и , следовательно, данная функция не является ни четной, ни нечетной, т. е. это функция общего вида.

3. Возрастающие и убывающие функции.

Определение. Функция называется возрастающей в промежутке , если для любых и , принадлежащих этому промежутку, при имеет место неравенство .

Определение. Функция называется убывающей в промежутке , если для любых и , принадлежащих этому промежутку, при имеет место неравенство .

Определение. Функция называется убывающей, если для любых и из области определения функции, при имеет место неравенство .

Определение. Функция называется возрастающей, если для любых и из области определения функции, при имеет место неравенство .

Только убывающие или только возрастающие функции называются монотонными, а промежутки возрастания и убывания называются промежутками монотонности.

Пример 4. Найти промежутки монотонности данной функции по ее графику:

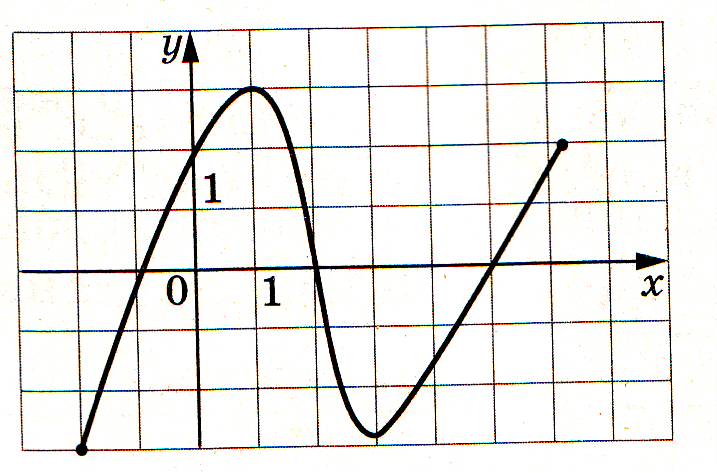
Решение. Функция возрастает при и убывает при .

4. Корень п-ой степени. Степень с рациональным показателем.

Определение. Арифметическим корнем -й степени из числа называют неотрицательное число, -я степень которого равна .

При нечетном существует корень -й степени из любого числа и при том только один.

При четном существуют два корня -й степени из любого положительного числа ; корень из нуля равен нулю; корней четной степени из отрицательного числа не существует.

Основные свойства корней

5. , (если то )

6. Для любых чисел , таких, что выполняется неравенство .

7. , если , или , если и - четное.

Определение. Степенью с рациональным показателем называется выражение вида .

Основные свойства степеней

6. Пусть -рациональное число и . Тогда , .

7. Для любых рациональных чисел из неравенства следует, что и .

Пример 1.

1) Заменить степень с рациональным показателем корнем с целым показателем и упростить:

2) Заменить корень с целым показателем степенью с рациональным показателем и упростить:

Решение.

1) ,

,

.

2) ,

,

.

Пример2. Найти значение выражения .

Решение.

Пример 3. Преобразовать выражения:

1) ; 2) .

Решение.

1) ;

2) .

В данном примере степень с меньшим показателем принимается за новое основание, а все другие степени выражаются через это новое основание.

Пример 4

Преобразовать выражение .

Решение.

=.

5. Степенная функция.

Определение. Степенной функцией с показателем называется функция, заданная формулой

Если >1, то степенная функция определена и при х=0, т. к. .

При целых степенная функция определена и для .

При четных эта функция четная, а при нечетных - нечетная.

При степенная функция убывает на промежутке . При степенная функция возрастает при ,т. е. на промежутке

6. Показательная функция.

Определение. Функция, заданная формулой , где , называется показательной функцией с основанием а.

Свойства показательной функции.

• Область определения - множество R действительных чисел, т. е. или .

• Множество значений - множество R всех положительных действительных чисел, т. е. .

• Функция общего вида.

• При функция возрастает на всей области определения; при функция убывает на всей области определения.

• Графиком показательной функции является кривая, лежащая в верхней полуплоскости и проходящая через точку (0; 1).

Существует постоянная е2,71828184... Показательная функция с основанием е называется экспонентой().

7. Показательные уравнения и неравенства.

Определение. Показательным уравнением называется уравнение, в котором неизвестное содержится только в показателе степени.

Рассмотрим простейшее показательное уравнение

,

где >0, . Область значений функций - множество положительных чисел. Поэтому, если или данное уравнение не имеет решения.

При положительном функция

на множестве действительных чисел возрастает, если основание больше 1, и убывает, если . То есть, в этом случае уравнение имеет единственный корень. Чтобы его найти, нужно b представить в виде , т. е.

представить обе части уравнения в виде степеней с одинаковым основанием.

Пример 1 . Решить уравнение .

Решение.

Так как 49 = 7² , а = , поэтому данное уравнение можно записать в виде

.

В равных степенях при равных основаниях показатели равны. Следовательно, , то есть x = .

Ответ: .

Пример 2. Решить уравнение .

Решение.

Данное уравнение можно записать в виде

То есть. . Следовательно, х-1 = 0, х = 1.

Ответ: 1.

Пример 3. Решить уравнение .

Решение.

Введем замену: , тогда получим квадратное уравнение . Решая данное уравнение относительно , получим два корня: , т. е. и . Следовательно, .

Ответ: 1; 2.

Решение простейших показательных неравенств основано на свойстве показательной функции: функция возрастает, если основание больше 1, и убывает, если .

Пример 4. Решить неравенство .

Решение.

Так как 4 = , то данное неравенство можно представить в виде

. И так как основание меньше 1, показательная функция

убывает. Поэтому данное неравенство равносильно неравенству

7 - 3х > -2, откуда х < 3.

Ответ:

Пример 5. Решить неравенство

Решение.

В левой части неравенства вынесем общий множитель за скобки: .

Разделим обе части неравенства на положительный числовой множитель 7 - значение выражения, стоящего в скобках:

.

Представим правую часть неравенства в виде степени с основанием 2: .

Сравним показатели степеней:

.

Решая данное линейное неравенство получим:

.

Ответ: .

8. Логарифмы, их свойства. Логарифмическая функция.

Определение. Логарифмом по основанию () числа называется показатель степени, в которую нужно возвести основание чтобы получить число .

Обозначается . Отсюда по определению следует, что .

Данное равенство называется основным логарифмическим тождеством.

Свойства логарифмов

1)

2)

3)

4)

5)

Виды логарифмов

Логарифмы, основания которых равны 10, называют десятичными и обозначают .

Логарифмы, основания которых равны числу , называют натуральными и обозначают .

Формулы перехода к другому основанию: ; или .

Для упрощения выражений, содержащих логарифмы, полезно знать следующие формулы: 1) ,

2) .

Примеры преобразования логарифмических выражений

Пример 1. Найти число , если .

Решение.

Преобразуем правую часть равенства, пользуясь свойствами логарифмов

,

т. е. , и поэтому .

Пример 2. Найти значение выражения .

Решение.

Преобразуем числитель и знаменатель дроби, пользуясь основными свойствами логарифмов

Следовательно,

Пример 3. Найти значение выражения .

Решение.

Преобразуем каждый множитель, пользуясь основными свойствами логарифмов

Следовательно,

.

Пример 4. Прологарифмировать по основанию 2: .

Решение.

Пример 5. Вычислить: 4.

Решение.

Упростим показатель степени:

Следовательно, 4

9. Логарифмическая функция

Определение. Функцию, заданную формулой называют логарифмической функцией с основанием , где и .

Свойства логарифмической функции.

• Область определения - множество R всех положительных действительных чисел, т. е. .

• Множество значений - множество R всех действительных чисел, т. е. .

• Функция общего вида.

• При функция возрастает на всей области определения; при функция убывает на всей области определения.

• Графиком логарифмической функции является кривая, лежащая в правой полуплоскости и проходящая через точку (1; 0).

10. Логарифмические уравнения и неравенства.

Логарифмические уравнения

Определение. Логарифмическим уравнением называется такое уравнение, в котором неизвестное содержится под знаком логарифма (в частности, в основании логарифма).

При решении таких уравнений обе части уравнения представляют в виде логарифмов с одинаковым основанием. У равных логарифмов с равными основаниями логарифмируемые выражения равны. После решения такого уравнения необходимо выполнить проверку.

Пример 1. Решить уравнение .

Решение.

По определению логарифма , то есть ,

или . Решим систему: . Корнями данного квадратного уравнения являются числа -5 и 1. Решением квадратного неравенства будет объединение числовых промежутков . Корни уравнения принадлежат объединению полученных промежутков, следовательно, эти числа являются корнями логарифмического уравнения.

Ответ: -5; 1.

Пример 2. Решить уравнение

Решение.

Это уравнение определено для тех значений х, при которых выполнены неравенства . Для этих х данное уравнение равносильно уравнению 2х +3 = х+1. Следовательно, решим систему: .

Отсюда х = -2. Однако, число х = -2 не удовлетворяет неравенству

х+1 > 0. Следовательно, данное уравнение корней не имеет.

Ответ: нет корней.

Пример 3. Решить уравнение

Решение.

Этому уравнению удовлетворяют все числа, больше 0, и отличные от 1, при условии, что справедливо равенство , то есть

Из решения данной системы следует: -2х + 4 = 0, откуда х = 2.

Ответ: 2.

Логарифмические неравенства

Решение логарифмических неравенств основано на свойстве логарифмической функции: функция возрастает, если основание больше 1, и убывает, если 0 < а < 1.

Пример 4. Решим неравенство

Решение.

Число -2 равно . Поэтому данное неравенство можно переписать в виде

Логарифмическая функция с основанием определена и убывает на множестве положительных чисел. Следовательно, неравенству удовлетворяют такие числа х, для которых выполняется условие , откуда .

Ответ: (-2; 2,5).

Контрольные вопросы

1. Сформулируйте определение функции.

2. Что называется областью определения функции?

3. Что называется областью значений функции?

4. Какими способами может быть задана функция?

5. Как находится область определения функции?

6. Какие функции называются четными и как они исследуются на четность?

7. Какие функции называются нечетными и как они исследуются на нечетность?

8. Какие функции называются возрастающими?

9. Какие функции называются убывающими?

10. Какие функции называются монотонными?

11. Что такое «промежутки монотонности»?

12. Определение степенной функции. Виды степенной функции в зависимости от показателя степени. Свойства этих функций.

13. Определение степени с целым, рациональным и действительным показателем.

14. Свойства степени с рациональным показателем.

15. Определение корня с целым показателем.

16. Свойства корня с целым показателем.

17. Формулы сокращенного умножения.

18. Определение показательной функции.

19. Свойства показательной функции, ее график, зависимость графика от основания.

20. Понятие показательного уравнения.

21. Рассказать свойство показательной функции, на котором основано решение показательных неравенств.

22. Понятие логарифмического уравнения.

23. Свойство логарифмической функции, на котором основано решение логарифмических неравенств.

24. Свойства логарифмов.

25. Определение и свойства логарифмической функции.

26. Зависимость графика логарифмической функции от основания логарифма.

Домашнее задание/ задание для самостоятельной работы:

1 А. Н. Колмогоров. стр. 224, 232, 238, 259.

№ 1. Найти значение числового выражения:

№ 430. а) 243; б) .

№ 431. а) : ; б) .

№ 437. а) ;

б) .

№448. а) ; б) .

№ 2. Построить в одной системе координат графики функций:

а) и ; б) и ; в) и .

№ 3. Построить графики функций:

1) а) ; б) ; в) ; г) ;

2) а) ; б) ; в) ; г) ;

3) а) ; б) ; в) ; г) .

№ 4. Решить показательные уравнения и неравенства:

№ 460. а) ; б) . № 461. а) ; б) .

№ 462. а) ; б) .

№ 463. а) ; б) .

№ 464. а) ; б) .

№ 466. а) ; б) . № 467. а) ; б) .

№ 472. а) ; б) .

№ 473. а) ; б) .

№ 5. Найти число х:

№ 484. а) ; б) .

№ 497. а) ;

б) .

№ 6. Упростить выражения, пользуясь основным логарифмическим тождеством:

№ 488. а) ; б) . № 489. а) ; б) .

№ 490. а) ; б) .

№ 7. Прологарифмировать:

№ 491. По основанию 3: а) ; б) .

№ 492. По основанию 10: а) ; б) .

№ 8. Вычислить:

№ 495. а) ; б) . № 496. а) ; б) .

№ 66. (стр. 286) в) ; б) .

№ 9. Решить логарифмические уравнения и неравенства:

№ 513 а) ; б) .

№ 514. а) ; б) .

№ 516. а) ; б) . № 517. а) ; б) .

№ 518. а) ; б) .

№ 519. а) ; б) .

№ 520. а) ; б) .

№ 525. а) ; б) .