Экзаменационная работа по математике за курс 8 класса (3 модуля)

Экзаменационная работа по математике за курс 8 класса

Вариант 1

Часть 1

Модуль «Алгебра»

1. Найти значение выражения: .

2. Какое из чисел отмечено на координатной прямой точкой А?

1. ;

2. ;

3. ;

4. .

3. Представьте выражение в виде степени с основанием c.

1. ;

2. ;

3. ;

4. .

4. Решите уравнение. Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера.

9. 

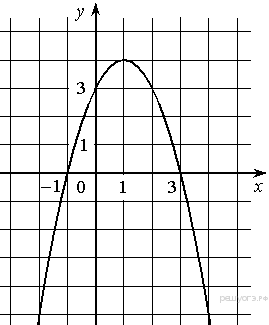
13. 1) f(−1) = f(3).

14. 2) Наибольшее значение функции равно 3.

15. 3) f(x)>0 при −1

6. Упростите выражение и найдите его значение при x = 4 . В ответ запишите полученное число.

7. Решите неравенство . В ответе укажите номер правильного варианта.

16. 1) ;

17. 2) ;

18. 3) ;

19. 4) .

21. Модуль «Геометрия»

8. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.

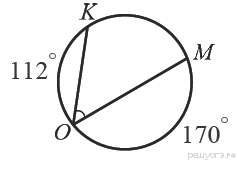
9. Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно (см. рисунок).

10. Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.

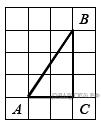
11. Найдите тангенс угла А треугольника ABC, изображённого на рисунке.

12. Какие из следующих утверждений верны?

22. 1) Сумма углов выпуклого четырехугольника равна 180°.

23. 2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.

24. 3) Диагонали квадрата делят его углы пополам.

26. Модуль «Реальная математика»

13. В таблице даны результаты забега мальчиков 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,5 с.

29. I

30. II

31. III

32. IV

33. Время (в с)

34. 10,6

35. 9,7

36. 10,1

37. 11,4

38. Укажите номера дорожек, по которым бежали мальчики, получившие зачет.

39. 1) только I

40. 2) только II

41. 3) I, IV

42. 4) II, III

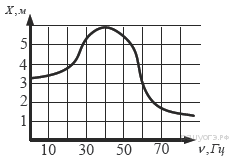
14. На рисунке изображен график зависимости амплитуды вынужденных колебаний от частоты колебаний. По вертикальной оси откладывается амплитуда (в м), по горизонтальной - частота колебаний (в Гц). По рисунку определите частоту колебаний, если амплитуда была равна 3 м.

15. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма в рублях из этой прибыли должна пойти на выплату частным акционерам?

16. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 5 м. Найдите длину троса.

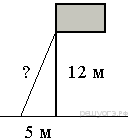
17. В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.

18. Часть 2

19. Модуль «Алгебра»

20. Решите неравенство .

21. Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.

22. Постройте график функции и определите, при каких значениях c прямая y = c имеет с графиком ровно две общие точки.

24. Модуль «Геометрия»

25. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56.

26. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке E стороны BC. Докажите, что E - середина BC.

28. Экзаменационная работа по математике за курс 8 класса

29. Вариант 2

30. Часть 1

31. Модуль «Алгебра»

1. Найти значение выражения: .

2. Одна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?

1. A;

2. B;

3. C;

4. D.

3. Представьте выражение в виде степени с основанием a.

1. ;

2. ;

3. ;

4. .

4. Решите уравнение . Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. На рисунке изображён график квадратичной функции y = f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера.

5. 

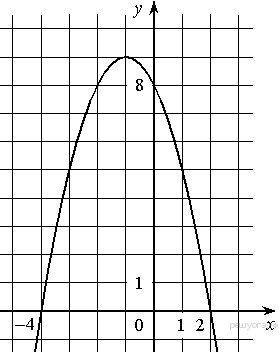
8. 1) Наибольшее значение функции равно 9.

9. 2) f(0) > f(1).

10. 3) f( x )>0 при x<0.

6. Упростите выражение и найдите его значение при a = 6. В ответ запишите полученное число.

7. Решите неравенство . В ответе укажите номер правильного варианта.

11. 1) ;

12. 2) ;

13. 3) ;

14. 4) .

15. Модуль «Геометрия»

8. Один угол параллелограмма в четырнадцать раз больше другого. Найдите меньший угол. Ответ дайте в градусах.

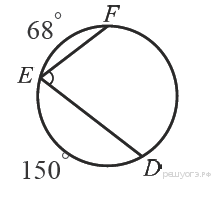
9. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно (см. рисунок).

10. Основания равнобедренной трапеции равны 15 и 25, а её боковые стороны равны 13. Найдите площадь трапеции.

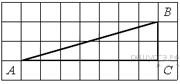
11. Найдите тангенс угла В треугольника ABC, изображённого на рисунке.

12. Укажите номера верных утверждений.

16. 1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

17. 2) Существует квадрат, который не является ромбом.

18. 3) Сумма углов любого треугольника равна 180°.

20. Модуль «Реальная математика»

13. В таблице даны результаты забега девочек 8 класса на дистанцию 60 м. Зачет выставляется при условии, что показан результат не хуже 10,8 с.

15. I

16. II

17. III

18. IV

19. Время (в с)

20. 10,7

21. 10,9

22. 9,8

23. 11,4

24. Укажите номера дорожек, по которым бежали девочки, не получившие зачет.

25. 1) только II

26. 2) только III

27. 3) II, IV

28. 4) I, III

29. На рисунке изображен график зависимости амплитуды вынужденных колебаний от частоты колебаний. По вертикальной оси откладывается амплитуда (в м), по горизонтальной ‒ частота колебаний (в Гц). По рисунку определите частоту колебаний, если амплитуда была равна 1 м.

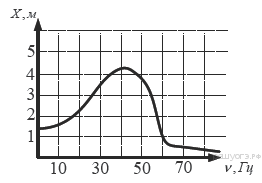
30. Государству принадлежит 90% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 20 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?

31. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.

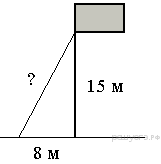
32. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с вишней.

33. Часть 2

34. Модуль «Алгебра»

35. Решите неравенство .

36. Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.

37. Постройте график функции и определите, при каких значениях c прямая y = c имеет с графиком ровно две общие точки.

39. Модуль «Геометрия»

40. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 16, DC = 24, AC = 25.

41. В параллелограмме ABCD точка E ‒ середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм ‒ прямоугольник.

45. ОТВЕТЫ