Учителю
Рабочая программа по математике для 10-11 классов

Рабочая программа по математике для 10-11 классов

Автор публикации: Итбаева Г.М.

Дата публикации: 09.10.2016

Краткое описание:

предварительный просмотр материала

Пояснительная записка

Рабочая программа профильного курса «Математика» для 10-11 класса составлена на основе следующих нормативно - правовых документов:

Федеральный Закон «Об образовании в Российской Федерации» (от 29.12. 2012 г. № 273-ФЗ);
Федеральный Закон от 01.12.2007 г. № 309 (ред. от 23.07.2013 г.) «О внесении изменений в отдельные законодательные акты Российской Федерации в части изменения и структуры Государственного образовательного стандарта»;
Приказ Минобразования России от 05.03.2004 г. № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»;
Приказ Минобрнауки России от 31.03.2014 г. № 253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования »;
Приказ Минобразования России от 09.03.2004 г. № 1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования»;
Учебный план МОАУ башкирская гимназия- интернат с.Исянгулово ;
Положение о рабочей программе, рассмотренное и принятое на педагогическом совете №7 от 24 июня 2016 года, утвержденное приказом №140 от 27 июня 2016 года

Цель курса:

Способствовать формированию математической культуры, формированию интеллектуально- грамотной личности, способной самостоятельно получать знания, осмысленно выбирать профессию и специальность в соответствии с заявленным профилем образования в условиях модернизации системы образования РФ.

Изучение математики в 10-11 классах на профильном уровне направлено на достижение следующих целей:

формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;

воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.

В рамках указанных содержательных линий решаются следующие задачи:

систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
знакомство с основными идеями и методами математического анализа.
формирование умения использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных.

Место курса в базисном учебном плане

Согласно федеральному базисному учебному плану на изучение математики на профильном уровне в 10 и 11 классе в учебном плане отводится 6 часов в неделю, из которых предусмотрено 4 часов в неделю на изучение курса алгебры и начал математического анализа и 2 часа на изучение геометрии.

Для реализации обучения математике по данной программе используется комплект:

Авторская примерная программа А. Г. Мордковича (профильный уровень). (Алгебра и начала математического анализа. 10-11 классы./ авт.- сост. И.И. Зубарева, А.Г. Мордкович/ М.: Мнемозина)
Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П.В. Семенов. / М.: Мнемозина
Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) / [А. Г. Мордкович и др.]; под ред. А.Г. Мордковича / М.: Мнемозина
Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (профильный уровень) / [А. Г. Мордкович и др.]; под ред. А.Г. Мордковича / М.: Мнемозина

Литература для учащихся:

Ф. Ф. Лысенко Математика ЕГЭ - 2014 . Математика. - Ростов-на-Дону: Легион;
Ф.Ф. Лысенко Математика ЕГЭ. Учебно-тренировочные тесты. - Ростов-на-Дону: Легион;

для учителя:

Глизбург В.И. Алгебра и начала анализа, 10 класс. Профильный уровень. Контрольные работы. - М.: Мнемозина;

Интернет - ресурсы:

Министерство образования РФ

www.informika.ru/</<br>
www.ed.gov.ru/

www.edu.ru/

Тестирование online: 5 - 11 классы

www.kokch.kts.ru/cdo/

Педагогическая мастерская, уроки в Интернет и многое другое

Планируемые результаты

«Алгебра и начала анализа»

10 класс

Тема 1. «Повторение»

Функция. Способы задания функции. Область определения, область значения функции. Графики функций. Свойства функций.

В результате изучения данной темы учащиеся должны знать:

что функция - это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.

уметь:

находить значения функции, заданной формулой, таблицей, графиком по ее аргументу.
находить значение аргумента по значению функции, заданной графиком или таблицей.
определять свойства функции по ее графику.
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств.
строить графики различных функций с помощью параллельных переносов.
интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы.

Тема 2. «Действительные числа»

Натуральные и целые числа. Рациональные числа. Иррациональные числа. Множество действительных чисел. Модуль действительного числа. Метод математической индукции.

В результате изучения данной темы учащийся должен уметь:

выполнять арифметические действия.
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
понятие простых и составных чисел, деление с остатком.

находить общий делитель и наименьшее общее кратное нескольких натуральных чисел.
понятие рационального и иррационального числа, действительные числа
числовая прямая; числовые неравенства; числовые промежутки.
модуль действительного числа; метод математической индукции.

Тема 3. «Числовые функции»

Определение числовой функции и способы ее задания. Свойства функций. Периодические функции. Обратная функция.

В результате изучения данной темы учащийся должен уметь:

определение числовой функции и способы ее задания.
свойства функций (возрастающая, убывающая, ограниченность, наименьшее и наибольшее значение функции, точка минимума и максимума функции, выпуклость функции, четность и нечетность, периодические функции)
понятие обратной функции.

Тема 4. «Тригонометрические функции»

Числовая окружность. Числовая окружность на координатной плоскости. Синус и косинус, тангенс и котангенс числа. Тригонометрические функции числового аргумента, их свойства и графики. Градусное и радианное измерение углов; тригонометрические функции числового, углового аргумента.

Основные тригонометрические тождества, связывающие функции одного и того же аргумент, их применение для вычисления значений тригонометрических функций некоторого аргумента по известному значению одной из тригонометрических функций того же аргумента. Формулы приведения.

Преобразование графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой у=х, растяжение и сжатие вдоль осей координат. Построение графика функции y=mf(x) и y=f(kx), если известен график функции y=f(x). Периодичность функций. График гармонического колебания.

В результате изучения данной темы учащиеся должны знать:

определение тригонометрической функции,
свойства тригонометрических функций, их графики,
основное тригонометрическое тождество,
формулы приведения;

уметь:

находить числа, задаваемые точками на единичной окружности
определять значения тригонометрических функций, используя единичную окружность,
решать простейшие тригонометрические уравнения в частных случаях,
проводить преобразование тригонометрических выражений, используя основные тригонометрические тождества,
находить значение одной тригонометрической функции через значение другой,
определять значение тригонометрической функции,
строить графики тригонометрических функций, выполнять преобразования графиков,
находить основной период тригонометрической функции.
преобразовывать тригонометрические функции с помощью формул приведения.

Тема 5. «Тригонометрические уравнения»

Арксинус, арккосинус, арктангенс, арккотангенс числа. Решение простейших тригонометрических уравнений. Методы решения тригонометрических уравнений: разложение на множители, введение новой переменной. Однородные уравнения. Простейшие тригонометрические неравенства.

В результате изучения данной темы учащиеся должны знать:

алгоритм решения тригонометрических уравнений,
общие формулы корней тригонометрических уравнений,

уметь:

решать тригонометрические уравнения и их системы,
изображать на координатной плоскости решения уравнений и систем.

Тема 6. «Преобразование тригонометрических выражений»

Формулы сложения аргументов, формулы двойных углов, понижения степени. Преобразование сумм тригонометрических функций в произведение, преобразование произведений в суммы. Преобразования тригонометрических выражений. Решение тригонометрических уравнений и неравенств.

В результате изучения данной темы учащиеся должны знать:

формулы тригонометрии,
формулы разности и суммы двух аргументов, формулы двойного аргумента,

уметь:

преобразовывать суммы тригонометрических функций в произведение и произведение в сумму;
проводить преобразование тригонометрических выражений, используя данные формулы.

Тема 7. «Производная»

Числовые последовательности. Предел числовой последовательности. Сумма бесконечной геометрической прогрессии. Понятие предела функции (на бесконечности и в точке).

Задачи о касательной к графику функции и о скорости прямолинейного движения, приводящие к понятию производной. Производная как новая математическая модель, ее определение, геометрический и механический смысл. Уравнение касательной к графику функции. Производная суммы, произведения, частного. Дифференцирование степенной функции, дифференцирование тригонометрических функций. Производная y=f(kx+m).

Применение производной для исследования функций на монотонность и экстремумы. Отыскание наибольших и наименьших значений функций. Вертикальные и горизонтальные асимптоты. Графики дробно-линейных функций.

Решение в прикладных задача. Нахождение скорости для процесса, заданного формулой или графиком. Вторая производная и ее физический смысл.

В результате изучения данной темы учащиеся должны знать:

геометрический и механический смысл производной,
правила вычисления производной,
формулы нахождения производных,
алгоритм отыскания производной,
составление уравнения касательной к графику функции,
исследование функций на монотонность и экстремум,
отыскание наибольшего и наименьшего значений,
непрерывность функции на промежутках.

уметь:

вычислять производные, применяя правила вычисления производных, используя справочные материалы,
исследовать функции и строить их графики с помощью производной,
решать задачи с применением уравнения касательной к графику функции,
решать задачи на нахождение наибольшего и наименьшего значения функции на промежутке.

Тема 8. «Комплексные числа»

Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа.

Алгебраическая и арифметическая формы записи комплексных чисел. Арифметические над комплексными числами в разных формах записи. Комплексно сопряженные числа. Возведение в натуральную степень (формула Муавра). Основная теория алгебры.

В результате изучения данной темы учащиеся должны знать:

выполнять действия с комплексными числами,
пользоваться математической интерпретацией комплексных чисел.
в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.

Тема 9. «Комбинаторика и вероятность»

Правило умножения. Комбинаторные задачи. Перестановки и факториалы. Выбор нескольких элементов. Биномиальные коэффициенты. Случайные события и их вероятности.

В результате изучения данной темы учащиеся должны знать:

знать правила умножения конечного числа испытаний;
число перестановок n-элементного множества;
решать простейшие комбинированные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля.
вычислять вероятность событий на основе подсчета числа исходов (простейшие случаи);

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации системного характера.

11 класс

Тема 1. «Повторение»

Тригонометрические уравнения и неравенства. Производная. Применение производной.

В результате изучения данной темы учащиеся должны

знать:

геометрический и механический смысл производной,
правила и формулы вычисления производной,

уметь:

вычислять производные, применяя правила вычисления производных,
исследовать функции и строить их графики с помощью производной,
решать задачи с применением уравнения касательной к графику функции,
решать задачи на нахождение наибольшего и наименьшего значения функции на промежутке,
проводить преобразование тригонометрических выражений, используя тригонометрические формулы.

Тема 2. «Многочлены»

Многочлены от одной переменной. Делимость многочленов. Деление многочленов с остатком. Рациональные корни многочленов с целыми коэффициентами. Схема Горнера. Теорема Безу. Число корней многочлена. Многочлены от двух переменных. Формулы сокращенного умножения для старших степеней. Бином Ньютона. Многочлены от нескольких переменных, симметрические многочлены.

В результате изучения данной темы учащиеся должны

знать:

находить корни многочленов с одной переменной, раскладывать многочлены на множители.
умение решать уравнения высших степеней.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

практических расчетов по формулам, включая формулы, содержащие степени, используя для необходимости справочные материалы и простейшие вычислительные устройства.

Тема 3. «Степени и корни. Степенные функции»

Понятие корня n-й степени из действительного числа. Функция у= 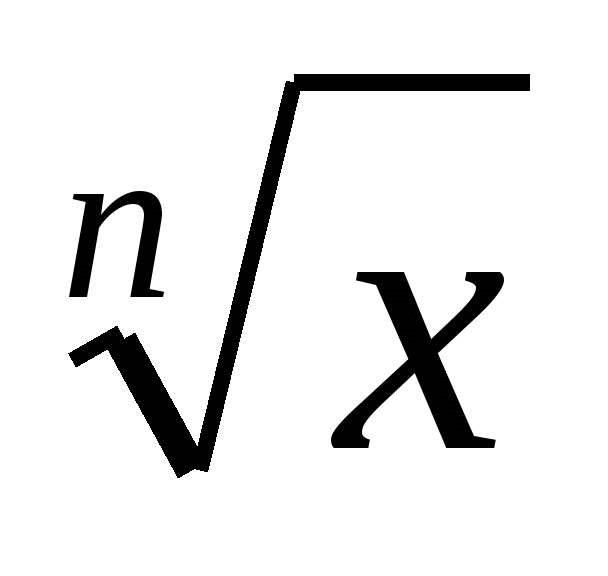, ее свойства и график. Свойства корня n-й степени. Обобщение понятия о показателе степени: степень с любым рациональным показателем. Понятие степени с действительным показателем. Свойства степени с рациональными показателями. Преобразование иррациональных выражений.

Степенная функция у=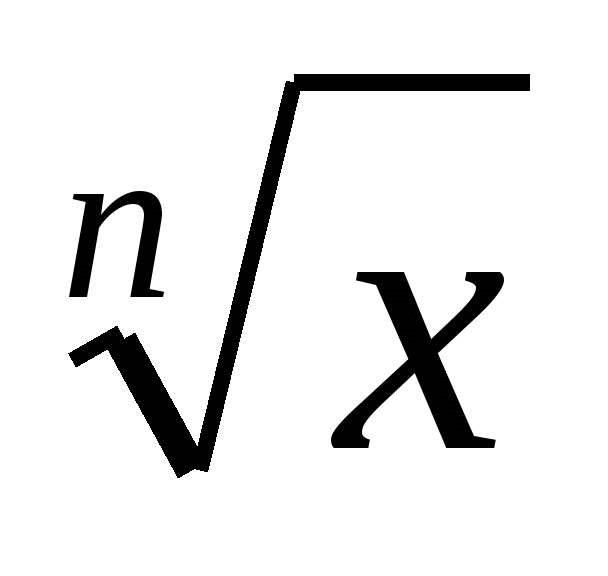( 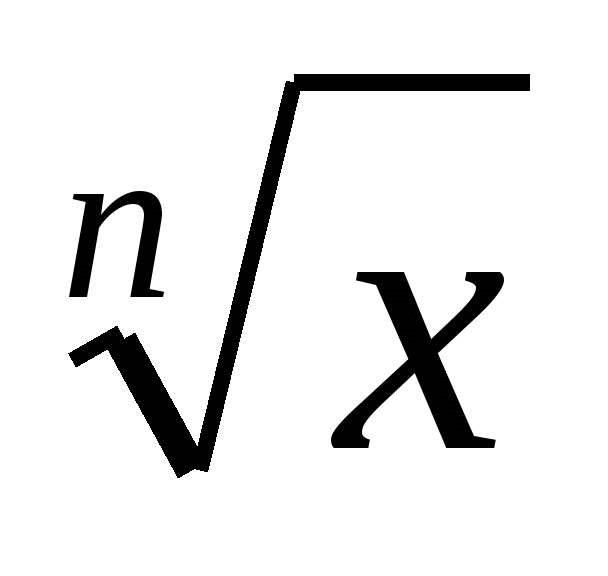- рациональное число), ее свойства (включая формулу дифференцирования) и график.

В результате изучения данной темы учащиеся должны знать:

свойства корня n-ой степени,
свойства степенной функции;

уметь:

находить значение корня n-ой степени,
проводить преобразование иррациональных выражений,
строить графики степенной функции с натуральным показателем.

Тема 4. «Показательная и логарифмическая функции»

Показательная функция, ее свойства и график. Показательные уравнения и неравенства, Понятие логарифма. Основное логарифмическое тождество.

Функция у=log_ax, ее свойства и график. Свойства логарифмов. Логарифмические уравнения и неравенства. Переход к новому основанию логарифма Дифференцирование показательной и логарифмической функций. Десятичный и натуральный логарифм. Число е.

В результате изучения данной темы учащиеся должны знать:

определения логарифма, его свойства,
свойства логарифмической и показательной функций,
алгоритм решения логарифмических и показательных уравнений и неравенств;

уметь:

находить значение логарифма, выражений, содержащих логарифм и показательные выражения,
проводить преобразования показательных выражений и выражений, содержащих логарифм,
решать показательные, логарифмические уравнения и неравенства,
решать системы показательных и логарифмических уравнений,
решать уравнения, неравенства и системы с применением графических представлений свойств показательной и логарифмической функций, выполнять преобразования графиков показательной и логарифмической функций.

Тема 5. «Первообразная и интеграл»

Первообразная и неопределенный интеграл. Определенный интеграл и его использование для вычисления площадей плоских фигур. Формула Ньютона-Лебница. Применение интеграла в физике и геометрии.

В результате изучения данной темы учащиеся должны знать:

алгоритм нахождения первообразной и вычисления определенного интеграла,
алгоритм вычисления площади криволинейной трапеции;

уметь:

вычислять первообразные элементарных функций, применяя правила вычисления первообразных,
вычислять площадь криволинейной трапеции.

Тема 6. «Элементы теории вероятностей и математической статистики»

Табличное и графическое представление данных. Числовые характеристики рядов данных.

Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.

Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.

В результате изучения данной темы учащиеся должны уметь:

решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера;

Теме 7. «Уравнения и неравенства Система уравнений и неравенств»

Равносильность уравнений, неравенств, систем. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Решение простейших систем с двумя переменными. Решение систем неравенств с одной переменной. Метод интервалов. Изображения на координатной плоскости множества решения уравнений и неравенств с двумя переменными и их систем.

В результате изучения данной темы учащиеся должны

знать/понимать:

основные методы решения алгебраических уравнений (разложения на множители, сведение к квадратному, введение новой переменной) и неравенств (метод интервалов),
алгоритмы решения рациональных уравнений, неравенств и их систем,алгоритмы решения иррациональных уравнений.

уметь:

решать рациональные, иррациональные уравнения и их системы,
решать рациональные неравенства и их системы, доказывать несложные неравенства,
решать текстовые задачи с помощью составления уравнений и неравенств, интерпретируя результат с учетом ограничений условия задачи,
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными,
находить приближенные решения уравнений и их систем, используя графический метод,
решать уравнения, неравенства и системы с применением графических
представлений, свойств функций, уравнения, системы уравнений, неравенства (обобщение и углубление тем 7-11 классов).

«Геометрия»

10 класс

Тема 1. «Введение»

Предмет стереометрии. Основные понятия стереометрии (точка, прямая, плоскость, пространство). Аксиомы стереометрии. Некоторые следствия из аксиом.

В результате изучения данной темы учащиеся должны знать:

- основные понятия стереометрии,

- аксиомы из стереометрии и следствия из них;

уметь:

- изображать точки, прямые, плоскости на проекционном чертеже при различном их взаимном расположении в пространстве.

Тема 2. «Параллельность прямых и плоскостей»

Параллельность прямых, прямой и плоскости. Взаимное расположение прямых в пространстве. Угол между двумя прямыми в пространстве. Параллельность плоскостей. Тетраэдр и параллелепипед.

В результате изучения данной темы учащиеся должны знать:

- случаи взаимного расположения прямых в пространстве (параллельные, пересекающиеся, скрещивающиеся), прямой и плоскости, плоскостей- в пространстве,

- признак параллельности прямой и плоскости,

- признаки и свойства скрещивающихся прямых;

уметь:

находить угол между двумя прямыми,
применять при доказательстве метод от противного,
изображать пространственные тела (тетраэдр и параллелепипед),
строить сечения тетраэдра и параллелепипеда

Тема 3. «Перпендикулярность прямых и плоскостей»

Перпендикулярность прямой и плоскости. Перпендикуляр и наклонные. Угол между прямой и плоскостью. Двугранный угол. Линейный угол двугранного угла. Расстояние от точки до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми. Теорема о трех перпендикулярах. Перпендикулярность плоскостей. Параллельное проектирование. Изображение пространственных фигур.

В результате изучения данной темы учащиеся должны знать:

признак перпендикулярности прямой и плоскости, двух плоскостей,
теорему о трех перпендикулярах;

уметь:

находить угол между двумя плоскостями, между прямой и плоскостью,
находить расстояние между прямой и плоскостью.

Тема 4. «Многогранники»

Понятие многогранника. Вершины, ребра, грани многогранника. Призма, ее основание, боковые ребра, высота, боковая поверхность. Прямая и наклонная призмы. Правильная призма. Параллелепипед. Куб. Пирамида, ее основания, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрия в кубе, в параллелепипеде, в призме, пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрии в окружающем мире. Сечения куба, призмы, пирамиды. Представления о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр, икосаэдр).

В результате изучения данной темы учащиеся должны знать:

- основные виды многогранников, их элементы,

уметь:

изображать многогранники,
решать задачи на вычисление с использованием сведений из тригонометрии, планиметрии.

Тема 5. «Векторы в пространстве»

Понятие вектора в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Компланарные векторы.

В результате изучения данной темы учащиеся должны знать:

понятие вектора в пространстве,
действия над векторами;

уметь:

- решать задачи, используя векторный метод.

11 класс

Тема 1. «Метод координат в пространстве»

Декартовы координаты в пространстве. Формула расстояния между двумя точками. Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Скалярное произведение векторов. Координаты вектора. Угол между векторами. Коллинеарные векторы. Разложение вектора по двум не коллинеарным векторам. Компланарные векторы. Разложение по трём не компланарным векторам. Формула расстояния от точки до плоскости. Уравнения сферы и плоскости.

В результате изучения темы учащиеся должны знать:

значение геометрии для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе.

В результате изучения темы учащиеся должны

знать:

формулы расстояния между точками,
определение скалярного произведения векторов,
понятие коллинеарных векторов,
определение компланарных векторов;

уметь:

- выполнять действия сложения, вычитания векторов и умножение вектора на число,

находить координаты точки в пространстве,
вычислять угол между векторами,

- приметь координатно-векторный метод для вычисления отношений, расстояний и углов.

Тема 2. «Цилиндр, конус и шар»

Цилиндр и конус. Усечённый конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию. Шар и сфера, их сечения, касательная плоскость к сфере.

В результате изучения темы учащиеся должны

знать:

определения тел вращения,
основные элементы цилиндра и конуса,
формулы для вычисления площадей поверхностей цилиндра, конуса и шара;

уметь:

проводить доказательные рассуждения при решении задач, доказывать основные теоремы, темы,
изображать цилиндр, конус и шар,

-решать задачи, опираясь на изученные свойства цилиндра, конуса и шара, применяя алгебраический и тригонометрический аппарат,
- строить осевые сечения и сечения параллельные основанию.

Тема 3. «Объемы тел и площади поверхности»

Понятие об объеме тела. Отношение объемов подобных тел. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхности цилиндра и конуса. Формулы объема шара и площади сферы. От землемерия к геометрии. "Начала" Евклида. Пифагор. Фалес.

Аксиоматика, определяемые и неопределяемые понятия. Теоремы. Евклидова геометрия и геометрия Лобачевского.

В результате изучения темы учащиеся должны

знать:

понятие объема тела,
формулы объема куба, прямоугольного параллелепипеда, призмы и цилиндра,
формулы объема пирамиды, конуса и шара,
формулы площади поверхности цилиндра конуса и сферы;

уметь:

соотносить стереометрические фигуры с их описаниями,
изображать взаимное расположение стереометрических фигур, выполнять чертёж по условию задачи,
вычислять объемы и площади поверхности пространственных тел и их простейших комбинаций

Содержание учебного курса

«Алгебра и начала анализа»

10 класс

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Уметь:обобщать и систематизировать знания по основным темам курса математики за 7-9 классы.

Действительные числа

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Индивидуальная

Знать и понимать: натуральные , целые числа; признаки делимости; простые и составные числа.

Уметь: применять понятия, связанные с делимостью целых чисел, при решении задач.

Числовые функции

Тестирование

Групповая работа

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Знать/ понимать: числовые функции, способы задания функций; Уметь: определять значения функции по значению аргумента при различных способах задания функции.

Тригонометрические функции

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Знать/ понимать: числовая окружность как можно на единичной окружности определять длины дуг и отрицательное направление обхода окружности, первый и второй макет. Уметь: используя числовую окружность, находить все числа, которым на числовой окружности они соответствуют

Тригонометрические уравнения

Групповая работа

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Тестирование

Уметь:вычислять некоторые значения обратных тригонометрических функций; решать простейшие тригонометрические уравнения и неравенства;производить отбор корней

Преобразование тригонометрических выражений

Групповая работа

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Тестирование

Знать/ понимать:формулы синуса и косинуса суммы и разности аргументов.Уметь: проводить преобразования тригонометрических выражений и решать тригонометрические уравнения и неравенства с использованием данных формул.

Комплексные числа

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Знать и понимать: натуральные , целые числа, комплексные числа; признаки делимости; простые и составные числа.

Уметь: применять понятия, связанные с делимостью комплексных чисел, при решении задач.

Производная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Знать/ понимать: числовая последовательность, свойства числовой последовательности.

Уметь:находить n-й член последовательности, строить график последовательности

Комбинаторика и вероятность

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Знать и понимать:классическое, геометрическое и статистическое определения вероятности формулы для вычисления вероятности ,статистические методы обработки информации. Уметь: вычислять вероятности событий на основе подсчета числа исходов. Уметь: обобщать и систематизировать знания по основным темам курса математики 10 класса

Повторение курса 10 класса

11 класс

Основной вид учебной деятельности

Повторение

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Уметь:обобщать и систематизировать знания по основным темам курса математики 10 класса

Многочлены

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Знать и понимать:многочлены от одной и нескольких переменных,симметрические и однородные многочлены; теорема Безу; схема Горнера.Уметь:выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств, пользоваться оценкой и прикидкой при практических расчетах.

Степени и корни. Степенные функции

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Знать и понимать: Корень п-й степени, арифметический корень п-й степени, основные свойства; Иррациональные уравнения и способы решения. Определение степени, свойства степени;Степенная функция, ее свойства и график:Формулы дифференцирования и интегрирования степенной функции:Формула для извлечения корня из комплексного числа.Уметь:Вычислять корни, преобразовывать выражения, содержащие корни; решать иррациональные уравнения различных видов; вычислять степени, преобразовывать выражения.

Показательная и логарифмическая функции

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Знать и понимать:показательные уравнения, их корни, неравенства и системы уравнений,определение логарифма, основное логарифмическое тождество, свойства логарифма,виды логарифмических уравнений, неравенств и систем, способы решения,определение, свойства показательной функции и ее график, формулы производной и первообразной

Первообразная и интеграл

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Знать и понимать:первообразная, связь с производной, основное свойство, общий вид, график первообразной, таблица первообразных,первообразная суммы, разности, первообразная функции с постоянным множителем, первообразная сложной функции, криволинейная трапеция, геометрический смысл первообразной, площадь криволинейной трапеции,интеграл функции, знак интеграла

Элементы теории вероятностей и математической статистики

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Знать и понимать: классическое, геометрическое и статистическое определения вероятности, формулы для вычисления вероятности, статистические методы обработки информации. Уметь: вычислять вероятности событий на основе подсчета числа исходов.

Уравнения и неравенства. Системы уравнений и неравенств

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Знать и понимать: понятие равносильности уравнений, неравенств, прием нахождения приближенных корней, общие методы решения уравнений и их систем, общие методы решения неравенств и их систем, методы решения уравнений и неравенств с модулем, методы решения уравнений и неравенств с параметрами. Уметь:решать рациональные, показательные и логарифмические уравнения и неравенства.

Геометрия

10 классФормы организации учебной деятельности

Основной вид учебной деятельности

Введение

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Формулировать основные аксиомы стереометрии. Доказывать следствия из аксиом. Решать задачи на применение аксиом и следствий из аксиом.

Параллельность прямых и плоскостей.

Тестирование

Групповая работа

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Формулировать определения параллельных прямых, скрещивающихся прямых., прямой параллельной плоскости. Формулировать и доказывать теоремы, выражающие их признаки и свойства. Распознавать взаимное положение прямых в реальных формах (на окружающих предметах, стереометрических моделях и т.д.) Формулировать определение угла между прямыми. Формулировать определение углов

Перпендикулярность прямых и плоскостей.

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Многогранник

Тестирование

Групповая работа

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Формулировать определение и приводить примеры многогранников. Формулировать определение и изображать призму. Формулировать определение и изображать пирамиду, усеченную пирамиду. Формулировать определение и изображать правильные многогранники. Решать задачи на вычисление площади поверхности различных многогранников. Распознавать многогранники, на чертежах, моделях и в реальном мире. Моделировать условие задачи и помощью чертежа или рисунка, проводить дополнительные построения в ходе решения.

Векторы в пространстве

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Формулировать определения и иллюстрировать понятие вектора, длины вектора, коллинеарных векторов, компланарных векторов, равных векторов. Выполнять операции над векторами. Находить разложение вектора по трем некомпланарным векторам. Выполнять проекты по темам использования векторного метода при решении задач на вычисления и доказательства. Использовать готовые компьютерные программы для поиска пути решения и иллюстрации решения задач.

Повторение

Тестирование

Групповая работа

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

значение математической науки для решения задач, возникающих в теории и на практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

Извлекать информацию из таблиц и диаграмм ,выполнять вычисления по табличным данным.Определять по диаграммам наибольшие и наименьшие данные,

Сравнивать величины.

Итого 10 класс

11 класс

Основной вид учебной деятельности

Метод координат в пространстве

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Объяснять и иллюстрировать понятие пространственной декартовой системы координат. Выводить и использовать формулы координат середины отрезка, расстояния между двумя точками пространства., уравнение прямой в пространстве. Вычислять длину, координаты вектора, скалярное произведение векторов. Находить угол между векторами

Цилиндр, конус, шар

Тестирование

Групповая работа

Работа в паре

Математический диктант

Индивидуальная

Устный опрос по карточкам

Формулировать определение и изображать цилиндр. Формулировать определение и изображать конус, усеченный конус. Формулировать определения и изображать сферу и шар. Формулировать определение плоскости касательной к сфере. Формулировать и доказывать теоремы, выражающие признаки и свойства плоскости касательной к сфере.

Объемы тел и площади их поверхностей

Индивидуальная

Устный опрос по карточкам

Тестирование

Групповая работа

Работа в паре

Математический диктант

Формулировать понятие объема фигуры. Формулировать и объяснять свойства объема. Выводить формулы объемов призмы, пирамиды, усеченной пирамиды, цилиндра, конуса, усеченного конуса, шара., шарового сегмента, шарового пояса. Решать задачи на вычисление объемов различных фигур , неопределенного интеграла.

Повторение

Устный опрос по карточкам

Тестирование

Индивидуальная

Групповая работа

Работа в паре

Математический диктант

Сравнивать величины.

Тематическое планирование

«Алгебра и начала анализа»

Наименование раздела

Количество часов

10 класс

11 класс

Всего

Повторение материала 7-9 классов

Действительные числа

Числовые функции

Тригонометрические функции

Тригонометрические уравнения

Преобразование тригонометрических выражений

Комплексные числа

Производная

Комбинаторика и вероятность

Повторение курса 10 класса

Многочлены

Степени и корни. Степенные функции

Показательная и логарифмическая функции

Первообразная и интеграл

Элементы теории вероятностей и математической статистики

Уравнения и неравенства. Системы уравнений и неравенств

Предэкзаменационная работа за курс полной средней школы

Обобщающие повторение

Итого

140

136

Тематическое планирование

«Геометрия»

⇧

⇩

скачать материал