Применение формул сокращенного умножения для вычисления квадратов чисел

Применение формул сокращенного умножения для вычисления квадратов чисел

Алгебра, 7 класс

Цель: сформулировать у учащихся умения и навыки применения формул сокращенного умножения при подъеме чисел до квадрата, уметь их применять при выполнении упражнений, решении задач, развивать логическое мышление, память, математическую речь, воспитывать внимательность, настойчивость.

Ход урока

1. Организационный момент.

Добрый день, дети!

На предыдущих уроках вы работали над выработкой навыков применения формул сокращенного умножения.

Вспомните эти формулы.

2. Актуализация опорных знаний.

Предлагаю вам восстановить тождества:

3. Постановка цели деятельности.

При применении формул сокращенного умножения появляются осложнения в возвышении в квадрат чисел. Например, можно вычислить в столбик, калькуляторами пользоваться нельзя. Поэтому, сегодня мы рассмотрим приемы возвышения в квадрат чисел, которые основываются на законах арифметических действий, формулах сокращенного умножения.

Вы будете применять эти навыки только на уроках алгебры, но и на уроках геометрии, физики, астрономии и других.

Итак, откроем тетради и запишем тему урока: «возведение в квадрат чисел».

4. Восприятие и осознание.

Рассмотрим пример:

, тому

;

;

.

По аналогии можно поднести до квадрата числа от 11 до 99.

Например:

;

;

;

.

Применим эту формулу для трицифрового числа:

;

;

.

По такой схеме можно поднести до квадрата числа от 101 до 999.

Например:

;

.

Какое же геометрическое объяснение такого подъема?

Рассмотрим задачу: найти площадь квадрата со стороной 35см.

Решим задачу с помощью модели. Имеем модель квадрата, сторона которого равна 35см.

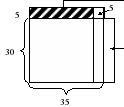
Передвигая, как показано на модели, заштрихованный прямоугольник, получаем прямоугольник со сторонами 40см. и 30см. Определив его площадь и добавив площадь квадрата со стороной 5см., получаем площадь квадрата со стороной 35см., поэтому

.

Дети, теперь остановимся на различных случаях применения формулы .

Задача. Найти площадь прямоугольника со сторонами 33см. и 27см.

Решения

Вместо этого найдем площадь квадрата со стороной 30см. и площадь квадрата со стороной 3 см., и от первого вычтем второе, то есть:

.

В некоторых случаях формулу разности квадратов записывают в таком виде:

Рассмотрим ее применение на примере:

1)

2)

3) или

Задача. Вычислить площадь квадрата со стороной 29,7 см.

Решения

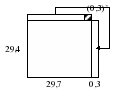
Надо вычислить (29,7)². вычисление площади квадрата со стороной 29,7 см. заменим вычислением площади прямоугольника со сторонами 30см. и 29,4 см., затем добавим площадь квадрата со стороной 0,3 см., то есть

Далее остановимся, дети, на геометрическом объяснении формулы , переписанной в обратном порядке, то есть .

Предлагаю вам построить квадрат со стороной a, его площадь равна а², отрезать от него квадрат со стороной b, площадь которого составляет b², тогда от части, что осталась, срезав прямоугольник и соответствующим образом передвинув его, получите прямоугольник со сторонами a-b и a+b.

Вычислить: 1) , 2) .

Решение

1) ;

2) .

5. Закрепление полученных знаний на примерах.

1. Вычислить:

а) ; б) ; в) ; г) ; д) ;

е) ; ж) ; з) .

2. Не производя вычислений определить площадь земельного участка больше и на сколько: у квадрата со стороной в 50 м. или прямоугольника со сторонами: а) 56м. и 44м.; б) 101,5м. и 98,5м?

Прошу учащихся ответить на вопросы.

1. Что показывает формула ?

(Показывает, как будет меняться площадь квадрата, если каждую его сторону уменьшить на несколько единиц.)

2. Что выражает формула ?

(Она выражает изменения площади квадрата, если каждую его сторону уменьшить на несколько единиц.)

3. На какой вопрос отвечает формула ?

(Она отвечает на вопрос, как изменяется площадь квадрата, если одну его сторону уменьшить на несколько единиц, а другую увеличить на столько же единиц, если периметр не переменный.)

Делаем вывод, что в первых двух случаях изменение площади зависит от стороны первоначального квадрата, так и от изменения стороны. В третьем случае изменение площади зависит только от изменения величины стороны, но не зависит от стороны первоначального квадрата.

6. Итог.

1. Чему вы научились на уроке?

2. Мы достигли цели урока?

7. Домашнее задание