'Построение графиков квадратичной функции'

МБОУ «Ивановская средняя общеобразовательная школа»

Интегрированный урок

(алгебра + информатика)

"Построение графиков квадратичной функции"

Трехлебова В.В. учитель информатики

Потехина О.М. учитель математики

Март 2012

Краткая аннотация урока

Учебный предмет - математика и информатика.

Уровень образования школьников: 8-й класс общеобразовательной школы, второй год изучения предмета.

Разделы программ:

математика - квадратичная функция, тема " График функции у=ах²+вх+с".

информатика - табличные вычисления на компьютере, тема " Построение графиков и диаграмм с помощью электронных таблиц".

Форма учебной работы - классно-урочная.

Продолжительность урока: 40 минут. Технологические особенности:

Дидактическое оснащение урока и ТСО: компьютер учителя, проектор, интерактивная доска, программа Smart Board (Notebook), цифровое пособие к уроку "Графики квадратичной функции", рабочие листы учащихся, компьютеры учащихся для выполнения групповой работы, файл График.xsl на каждый ученический компьютер, на экране: тема и цели урока

Цели:

• закрепить умение строить графики квадратичной функции и по графику определять ее основные свойства,

• используя свойства квадратичной функции решать задачи

• повышать уровень учебной мотивации с использованием компьютерных технологий, развивать логическое мышление.

К уроку подготовлена презентация. На экране учащиеся видят геометрические фигуры, в которых записаны уравнения. Натуральные числа, являющиеся решениями данных уравнений показывают очередность выполнения заданий на уроке.

Ход урока:

I этап Орг. момент

-Сегодня у нас с вами не совсем обычный урок. Мы попробуем объединить знания, полученные на уроках алгебры и информатики и привлечь компьютер к решению математических задач. У каждого из вас на столе лежат карточки с разными выражениями лиц. Определите фигуру, которая соответствует вашему эмоциональному состоянию на начало урока и поставьте около этой фигуры цифру 1. В конце урока вы сделаете то же самое. Это поможет мне определить ваше отношение к такой форме проведения урока.

Итак, начнем! Решив предложенный ребус, вы узнаете тему нашего урока.

- Итак, тема нашего урока «Квадратичная функция». Мы обобщим знания полученные при изучении квадратичной функции.

-Первый этап урока

Итак, переходим к первому этапу нашего урока. Вы должны заполнить пропуски, чтобы получилось верное утверждение или правильная формулировка определения, правила.

1. Функция у = aх² + bx + c, где а, b, c - заданные действительные числа, а 0, х - переменная, называется … ……. функцией.

2. График функции у = ах² при любом а 0 называют ...

3. Функция у = х² является … (возрастающей, убывающей) на промежутке х 0.

4. Значения х, при которых квадратичная функция равна нулю, называют … функции.

5. Точку пересечения параболы с осью симметрии называют … параболы.

6. При а >0 ветви параболы у = ах² направлены … .

7. Если а < 0 и х 0, функция у = ах² принимает …/положительные, отрицательные/ значения.

II. Подумай… /устные задания/.

-Переходим ко второму этапу урока. Но решением какого уравнения является натуральное число 2? /учащиеся говорят что число 2 входит во множество решений уравнения записанного на параллелограмме/.

За параллелограммом прячутся следующие задания:

1. Найдите координаты вершины параболы у=х²-4х+4

2. Найдите координаты точек пересечения квадратичной функции у=х²+х-2 с осью Ох.

3. Не производя построение графика, определите, наибольшее или наименьшее значение принимает квадратичная функция у=2-5х-3х²

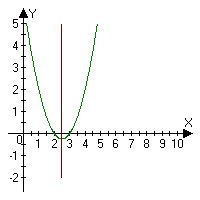4. По графику функции у=х² - 5х + 6

а)промежутки возрастания и убывания функции.

б)уравнение оси симметрии

в) координаты точки пересечения с осями Ох и Оу.

III. Работа в группах/. Работа с программой Microsoft Excel

Вам предлагается: Постройте графики и запишите свойства. № 451 (ж,з)

Разобрать как можно выполнить это задание с помощью программы Microsoft Excel.

Приблизительный ответ:

1. Составить таблицу значений зависимости переменной У от Х

2. Выделить таблицу

3. С помощью мастера диаграмм построить график

4. Определить те интервалы значений х, где график ниже оси х

5. Записать интервалы в тетрадь

(После обсуждения раздать карточки с алгоритмом выполнения задания)

Алгоритм построения графика функции у=х²+2х-3

1. Составить таблицу значений зависимости переменной У от Х

2. впишем в ячейку А1 - х

3. впишем в ячейку А2 - у=х2+2х-3

4. впишем в ячейку В1 начальное значение х - (-3)

5. впишем в ячейку С1 - (-2)

6. выделим содержимое ячеек В1 и С1, затем с помощью маркера автозаполнения автокопируем до ячейки Н1 (получим соответстветствующие значения от -3 до 3)

7. впишем в ячейку В2 формулу - =В1^2+2*x-3

8. скопируем формулу из ячейки В2 методом автозаполнения до ячейки Н2

2. Построение графика

• Выделить подготовленные данные, начиная с заголовка (А1:Н2)

• вызовем Мастер диаграмм и выберем вид диаграммы - точечная, тип - со сглаженными линиями без маркеров

• Укажем заголовок - (график у=х²+2х-3) и оси - (х,у)

• помещаем диаграмму на имеющемся листе - готово

IV. Тест.

Вариант I

1. Из функций: у = х² + 4, у = х - 3х² + 1, у = х⁶ -2х + 1, у = х - 1,у = (х + 1)² выберите квадратичные.

   • А) у = х² + 4, у = х - 3х² + 1;

   • Б) у = х² + 4, у = (х + 1)² ;

   • В) у = х² + 4, у = х - 3х² + 1, у = (х + 1)² ;

   • Г) у = х⁶ -2х + 1;

2. Найдите координаты вершины параболы у = - 6(х - 1)² .

   • А) (- 6; - 1);

   • Б) (1; 0);

   • В) (0; - 1);

   • Г) (1;0).

3. Найдите координаты точек пересечения параболы у = - 2х² + 8 с осью Ох.

   • А) (2;0);

   • Б) (0;0);

   • В) (0;4);

   • Г) (2;0), (-2;0).

4. Найдите координаты точек пересечения параболы у = х² + 10х - 11 с осью ординат.

   • А) (- 11;0);

   • Б) (0;- 11);

   • В) (0;0);

   • Г) (- 10; - 1).

5. На каком из графиков изображена функция у = - х² + х + 12?

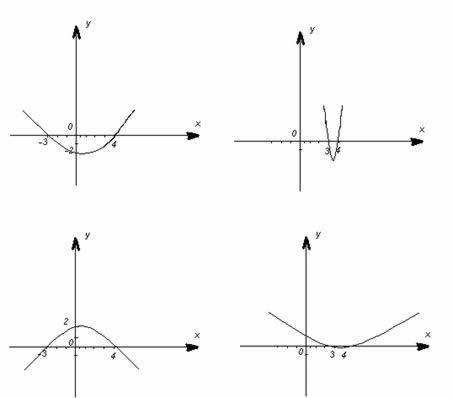
Вариант 2

1. Из функций у = х² + 3х + 1, у = х+ 5, у = - х² + 3х, у = (х - 4)² + 5, у = х + 3х + 2,у = х⁴ - 6х выберите квадратичные.

   1. А) у = х² + 3х + 1, у = х + 3х + 2;

   2. Б) у = х+ 5, у = х² + 3х + 1;

   3. В) у = х² + 3х + 1, у = - х² + 3х;

   4. Г) у = х² + 3х + 1, у = - х² + 3х, у = (х - 4)² + 5.

2. Найдите координаты вершины параболы = 2(х + 3)² - 5.

   1. А) (3; -5);

   2. Б) (3; 5);

   3. В) (-3; -5);

   4. Г) (-3; 5).

3. Найдите координаты точек пересечения параболы у = 3х² - 48 с осью абсцисс.

   1. А) (0; 4);

   2. Б) (4; 0), (-4; 0);

   3. В) (4; 0), (0; 0);

   4. Г) (4; 0).

4. Найдите координаты точки пересечения параболы у = х² +8х - 9 с осью Оу.

   1. А) (0; -9);

   2. Б)(0; 0);

   3. В) (-9; 0);

   4. Г) (9; -1).

5. На каком эскизе изображен график функции у = х² + 5х + 6?

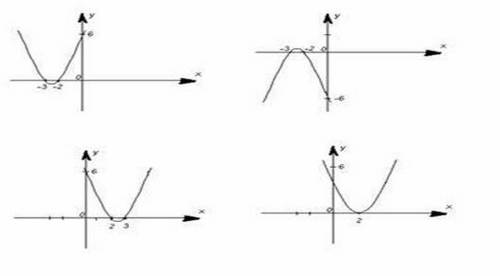
VI. Итог урока. Д/з.

1. Задания по информатике:

Постройте график квадратичная функция у=2х² -5х+3 и опишите её свойства.

2. Задания по алгебре:

1. Найдите координаты точек пересечения параболы у = х² + х - 12 с осями координат.

2. Не строя график функции у = х² - 4х + 6, найти ее наибольшее или наименьшее значение.

Приложение (у каждого на столе)

1. Постройте графики функций y= 2x²+8x-10 y= -3x² +6x-3

2. По графикам функций укажите:

• промежутки возрастания и убывания функции.

• уравнение оси симметрии

• координаты точки пересечения с осями Ох и Оу.