Вычисление площадей плоских фигур и объемов тел с помощью определенного интеграла. 11 класс

14.10.2016 г.

Открытый урок по алгебре и началам анализа в 11 «х» классе КГУ гимназии №46 г. Алматы учителя математики Бабенко Зинаиды Васильевны.

Эффективный урок, как основное условие качества знаний.

Тема урока: вычисление площадей плоских фигур и объемов тел с помощью определенного интеграла.

Цель урока:

Обучающая: систематизированию знаний, умений и навыков у учащегося при вычислении площадей и объемов тел с помощью определенного интеграла.

Развивающая мыслительную деятельность, математическую речь и графическую культуру учащегося, память.

Воспитывающая трудолюбие, самостоятельность, стремление к самореализации.

Тип урока: совершенствование знаний и способ деятельности.

Форма организации урока: тренинг.

Дидактическая обеспеченность: учебник, сборник задач по математике для поступающих во ВТУЗы под редакцией М.И. Сканави, дидактические материалы З.А. Жумагулова , Л.У. Жадраева общественно-гуманитарного направления 11 класса «Алгебра и начало анализа».

Ход урока:

1) Организационный момент

2)Проверка домашнего задания №62(б,г)-65(2).

3)Повторение: 1) Применение определенного интеграла в физике

4) Решить №70 (1,3), 71(1) из учебника

5) Самостоятельная работа С-4, стр. 10-11

6) Домашнее задание №70(2,4), 71(2,3,4). Подготовка к контрольной работе №1.

Домашняя работа №11.

№62(б)

S т ==)= (x + )|= 1+ - (-1+ )= + = 2 (кВ.ед.)

Ответ: 2

№62(г)

= ( + ) | = - + 1 = (кВ.ед)

Ответ:

№63 (2)

f(x)=

S найти

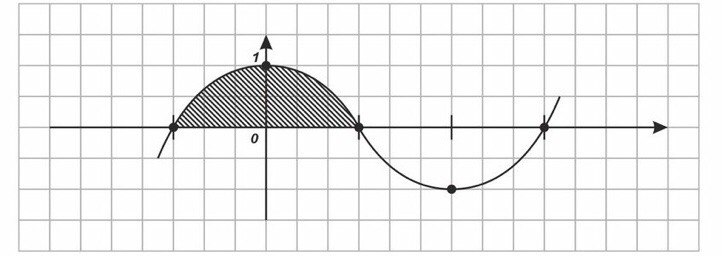
S= 2 = 2 | = 2 ( = 2*2 = 4 (кВ.ед.)

Ответ: 4 (кВ.ед.)

№64 (2)

Найти V тела, полученного вращением параболы y=3 от точки x=1 до точки x=2 вокруг оси OX.

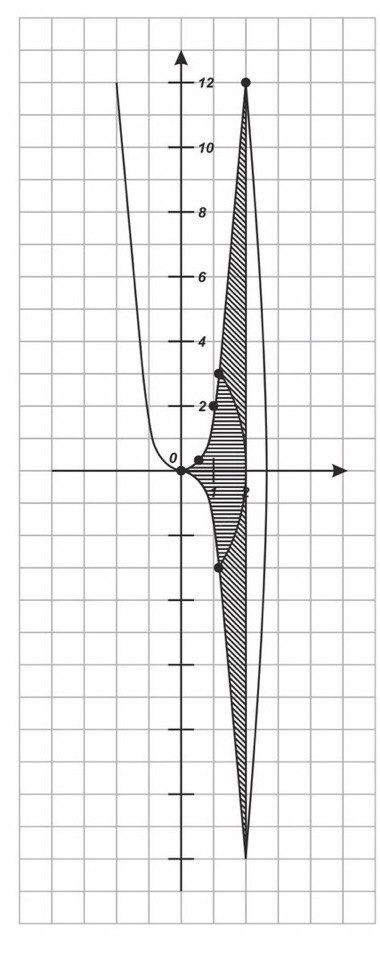
= = | = = *31 =

Ответ: куб.ед.

№ 65 (2)

S плоской фигуры ограниченной графиками y= , y=2x -

Решение.

Пределы интегрирования.

= 2x -

2 - 2x= 0

2 x (-1)=0

X₁=0 X₂=1 X₃= -1

Построим графики данных функций

y=2x -

y^| (x)= 2 -

X₁=

X₂= -

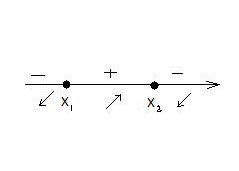
min (- ; -1,1)

max ( ; 1,1)

y= 2x -

дополнительные точки:

(0;0) (1;1) (2;-4) (-1;-1) (-2;4)

y= 2x - - функция нечетная

y= - нечетная

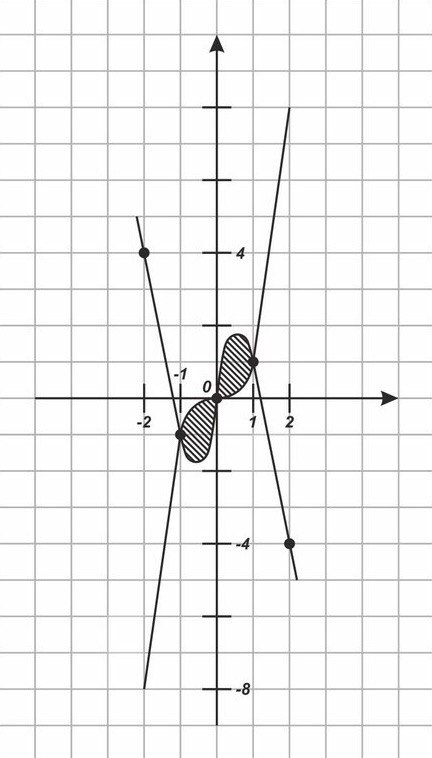
S искомой фигуры состоит из двух равных площадей.

S= 2 =2 = 2( ) |= 2(1-

Ответ: 1 кв.ед.

Классная работа.

Задание №1 из сборника. «Материальная точка движется вдоль прямой. Скорость точки изменяется по закону (t)= (). найти расстояние от точки до своего начального положения через 6 секунд после начала движения.»

Решение.

S(t)= dt= (| =216-24=192 (м)

Ответ: 192 м.

Задача 2. Сила упругости пружины, растянутой на 5 см равна 3 н. Какую работу надо произвести, чтобы растянуть пружину на 5 см.

Решение.

По закону Гука F=kx, где k-коэффициент пропорциональности, 5 см=0,05 м.

3=k*0,05

K=3:0,05=60

F=60x

A==|=30*0,0025=0,075 Дж

Ответ: 0,075 Дж

Сканави 15.274

Чему равен путь, пройденный точкой, движущейся прямолинейно, за отрезок времени от t₁ =1 до t₂ =4, если скорость точки (t)= (t-в секундах, - ) чему равно ускорение этой точки в момент t=2?

Решение.

1. S(t)==( + )|= +22,5=42+22,5=64,5 (м)

2. a(t)= ^|(t)

a(t)=()^|= 4t+ 3

a(2)=4*2+3=11 ()

Ответ: 64,5 (м); 11 ()

Сканави 15.275

Тело движется прямолинейно со скорость (t)= (t- в секундах,- в ).

Найти путь, пройденный телом за первые 7 секунд. Чему равно ускорение тела в момент t=7?

Решение.

1. S(t)=

2. ()^|= =a(t)

a(7)= =()

Ответ: 11,25 (м);()

№70

Найти площадь плоской фигуры, ограниченной линиями: y= и y= 3+x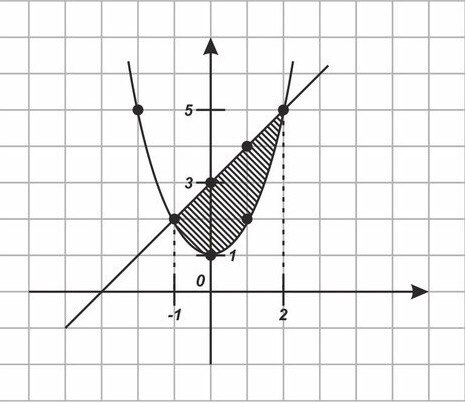

Решение.

1)Найдем пределы интегрирования:

= 3+x;

X₁=2

X₂=-1

2) построим графики

3. Чтобы найти S заштрихованной фигуры, надо от площади, ограниченной верхней функции вычесть площадь фигуры, ограниченной нижней функцией , т.е.

S=

Ответ :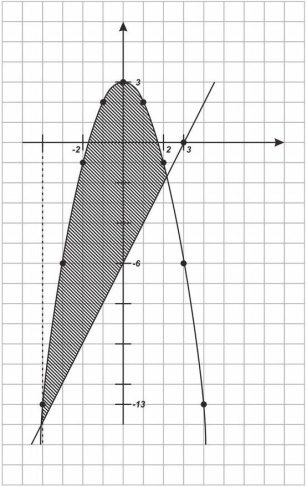

№70 (3)

y= и y= 2x-6

Решение.

1)Найдем пределы интегрирования:

= 2x-6

= 0

X₁=-1+

X₂=-1-

3. построим графики:

y=2x-6 ; (0;-6) (3;0)

4. S==

Ответ:

№71(1)

y=

y=

1. Пределы интегрирования:

X₁=3

X₂=5

2)графики:

y=

y^|=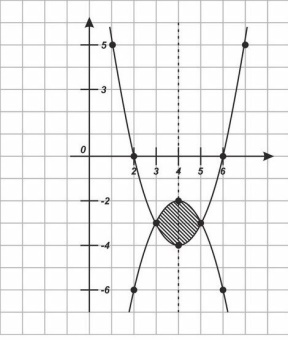

x₀=4

y₀=-4

(4;-4)- вершина параболы

(6;0) (2;0) (0;12)- точки пересечения с осями координат

y=

y^|=

x₀=4

y₀=-2

(4;-2)- вершина параболы, ветви вниз.

3) S= = - (кВ.ед.)

Ответ : (кВ.ед.)

Самостоятельная работа с-4

Вариант №1

1. S=

2. Вычислить S фигуры ограниченной y= ; y=2

Решение.

1. Пределы интегрирования

=2

X₁₌ 1

X₂₌ -1

2. Строим график

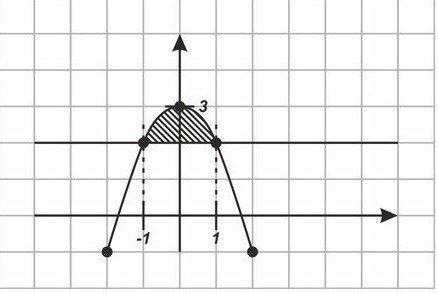
S= (кВ.ед.)

Ответ: (кВ.ед.)

3. По рисунку 6

S= (кв.ед)

Ответ: (кв.ед)

Найти S фигуры огр. графиком функции y= ,касательной к графику этой функции в точке с абсциссой x=0 и прямой x=1

Решение:

1. Уравнение касательной:

X₀=0

f^|(x)=x

f^|(x₀)=0

f(x₀)=2

y=2 - уравнение касательной

2. Строим графики

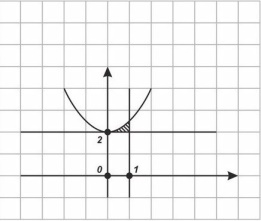
S=

Ответ:

4. Найти объем тела , полученного при вращении графика функции по оси OX от x=0 до x=1

Решение:

Строим графики:

V_т.в =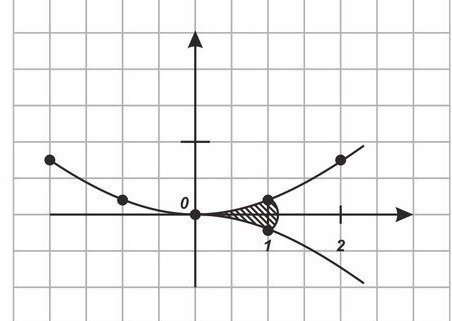

Ответ :

Вариант №2

1. По рисунку 7

S_ф=2

2. S_ф.огр ; y = 4

Решение :

1. Предел интегрирования

= 4

X₁₌ 1

X₂₌ -1

2)графики:

2. S=(кВ.ед.)

Ответ :(кВ.ед.)

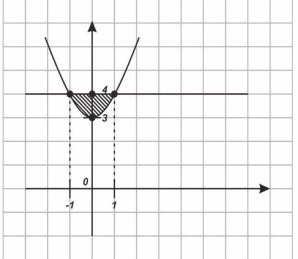
3. По рисунку 8

4. S_ф=(кВ.ед)

Ответ :(кВ.ед)

5. Найти S_ф, ограниченной графиком функции y=, касательной к графику в точке с абсциссой x=0 и прямой x= - 2

Решение:

1. Уравнение касательной

X₀=0

f^|(x)=2x

f^|(x₀)=0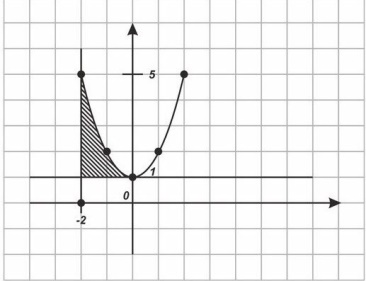

f(x₀)=1

y=1 - уравнение касательной

2. Строим графики

3. S_ф=( кВ.ед)

Ответ:( кВ.ед)

4. Найти объем тела, полученного при вращении графика функции y= по оси абсцисс от x=1 до x=2

</

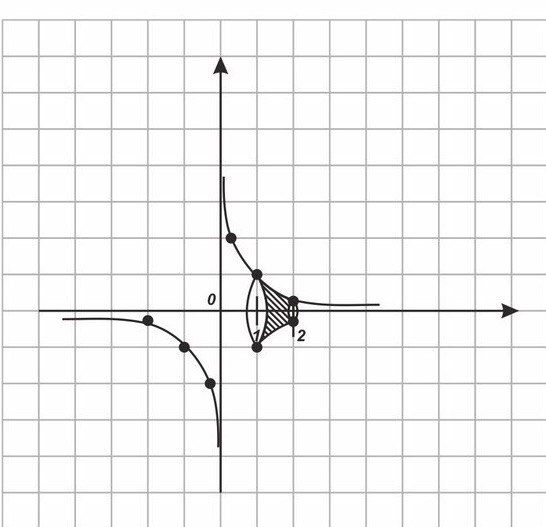
V_т.в.=(куб.ед)

Ответ :(куб.ед)

Домашнее задание : №70(3,4)-71(3,4)

Итоги урока:

11х:

1)Балтабаева Лютфи -5

2) Берик Нурила -5

3) Бижанова Амина-5

4)Керимова Адина-5

5) Леонтьева Арина-5

11м:

1)Казанова Полина-4

2)Койнова Арина-5

3)Пономарев Алексей-5

4)Байдилдин Акжан

5) Соловьева Анастасия -4