Приемы формирования и развития универсальных учебных действий на уроках математики в 5-6 классах

Приемы формирования и развития универсальных учебных действий на уроках

математики в 5-6 классах

Чаузова Надежда Степановна

учитель математики

Оглавление

1. Введение……………………………………………………………………………….3

2. Универсальные учебные действия и их виды……………………………………… 4

3. Приемы формирования и развития УУД на уроках математики…………………..8

4. Эффективность использования приемов для формирования УУД……………….13

5. Библиографический список…………………………………………………………15

1. Введение

Современное общество запрашивает человека обучаемого, способного самостоятельно учиться и многократно переучиваться в течение постоянно удлиняющейся жизни, готового к самостоятельным действиям и принятию решений. Федеральный государственный образовательный стандарт основного общего образования поставил на первое место в качестве главных результатов образования не предметные, а личностные и метапредметные - универсальные учебные действия (УУД).

Важнейшей задачей современной системы образования является формирование универсальных учебных действий, обеспечивающих школьникам умение учиться, способность к саморазвитию и самосовершенствованию. Все это достигается путем сознательного, активного присвоения учащимися социального опыта. При этом знания, умения и навыки рассматриваются как производные от соответствующих видов целенаправленных действий, т.е. они формируются, применяются и сохраняются в тесной связи с активными действиями самих учащихся. Овладение универсальными учебными действиями ведет к формированию способности самостоятельно усваивать новые знания, получение умений и компетенций, включая самостоятельную организацию процесса усвоения знаний. Поэтому современный урок - это, прежде всего, урок, направленный на формирование и развитие УУД. При его моделировании, учителю необходимо выбрать наиболее эффективные методы и приемы для формирования и развития УУД. Тогда возникает вопрос: с помощью каких заданий или приемов формировать и развивать у учащихся УУД. Этот вопрос заинтересовал нас. И мы поставили перед собой цель: разработать эффективные приемы формирования и развития универсальных учебных действий на уроках математики в 5-6 классах.

2.Универсальные учебные действия

Каковы же требования к результатам освоения образовательных программ? Это предметные результаты и УУД.

Предметные результаты включают освоенные обучающимися в ходе изучения учебного предмета умения специфические для данной предметной области. Это виды деятельности по получению нового знания в рамках учебного предмета, его преобразованию и применению в учебных, учебно-проектных и социально-проектных ситуациях, формирование научного типа мышления, научных представлений о ключевых теориях, типах и видах отношений, владение научной терминологией, ключевыми понятиями, методами и приемами.

Универсальные учебные действия - это действия, обеспечивающие овладение ключевыми компетенциями, составляющими основу умения учиться. Одной из особенностей УУД является их универсальность, которая проявляется в том, что они: 1) носят надпредметный, метапредметный характер;

2) обеспечивают целостность общекультурного, личностного и познавательного развития и саморазвития личности;

3) обеспечивают преемственность всех ступеней образовательного процесса;

4) лежат в основе организации и регуляции любой деятельности учащегося независимо от ее специально-предметного содержания;

5) обеспечивают этапы усвоения учебного содержания и формирования психологических способностей учащегося.

Виды универсальных учебных действий.

В составе основных видов универсальных учебных действий, диктуемом ключевыми целями общего образования, можно выделить четыре блока:
1) личностный; 2) регулятивный (включающий также действия саморегуляции); 3) познавательный; 4) коммуникативный.

В блок личностных универсальных учебных действий входят жизненное, личностное, профессиональное самоопределение; действия смыслообразования и нравственно-этического оценивания, реализуемые на основе ценностно-смысловой ориентации учащихся (готовности к жизненному и личностному самоопределению, знания моральных норм, умения выделить нравственный аспект поведения и соотносить поступки и события с принятыми этическими принципами), а также ориентации в социальных ролях и межличностных отношениях.

Самоопределение - определение человеком своего места в обществе и жизни в целом, выбор ценностных ориентиров определение своего "способа жизни" и места в обществе. В процессе самоопределения человек решает две задачи - построения индивидуальных жизненных смыслов и построения жизненных планов во временной перспективе (жизненного проектирования). Применительно к учебной деятельности следует особо выделить два типа действий, необходимых в личностно ориентированном обучении. Это, во-первых, действие смыслообразования, т. е. установление учащимися связи между целью учебной деятельности и ее мотивом, другими словами, между результатом-продуктом учения, побуждающим деятельность, и тем, ради чего она осуществляется. Ученик должен задаваться вопросом о том, «какое значение, смысл имеет для меня учение», и уметь находить ответ на него. Во-вторых, это действие нравственно-этического оценивания усваиваемого содержания, исходя из социальных и личностных ценностей.

В блок регулятивных действий включаются действия, обеспечивающие организацию учащимся своей учебной деятельности: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно; планирование - определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий; прогнозирование - предвосхищение результата и уровня усвоения, его временных характеристик; контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона; коррекция - внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его продукта; оценка - выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения. Наконец, элементы волевой саморегуляции как способности к мобилизации сил и энергии, способность к волевому усилию - к выбору в ситуации мотивационного конфликта, к преодолению препятствий.

В блоке универсальных действий познавательной направленности целесообразно различать общеучебные, включая знаково-символические; логические, действия постановки и решения проблем. В число общеучебных входят: самостоятельное выделение и формулирование познавательной цели; поиск и выделение необходимой информации; применение методов информационного поиска, в том числе с помощью компьютерных средств; знаково-символические действия, включая моделирование (преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта и преобразование модели с целью выявления общих законов, определяющих данную предметную область); умение структурировать знания; умение осознанно и произвольно строить речевое высказывание в устной и письменной форме; выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; смысловое чтение как осмысление цели чтения и выбор вида чтения в зависимости от цели; извлечение необходимой информации из прослушанных текстов различных жанров; определение основной и второстепенной информации; свободная ориентация и восприятие текстов художественного, научного, публицистического и официально-делового стилей; понимание и адекватная оценка языка средств массовой информации; умение адекватно, подробно, сжато, выборочно передавать содержание текста; составлять тексты различных жанров, соблюдая нормы построения текста (соответствие теме, жанру, стилю речи и др.).

Наряду с общеучебными также выделяются универсальные логические действия: анализ объектов с целью выделения признаков (существенных, несущественных); синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты; выбор оснований и критериев для сравнения, сериации, классификации объектов; подведение под понятия, выведение следствий; установление причинно-следственных связей, построение логической цепи рассуждений, доказательство; выдвижение гипотез и их обоснование.

Действия постановки и решения проблем включают формулирование проблемы и самостоятельное создание способов решения проблем творческого и поискового характера.

Коммуникативные действия обеспечивают социальную компетентность и учет позиции других людей, партнера по общению или деятельности, умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие и сотрудничество со сверстниками и взрослыми. Соответственно, в состав коммуникативных действий входят планирование учебного сотрудничества с учителем и сверстниками - определение цели, функций участников, способов взаимодействия; постановка вопросов - инициативное сотрудничество в поиске и сборе информации; разрешение конфликтов - выявление, идентификация проблемы, поиск и оценка альтернативных способов разрешения конфликта, принятие решения и его реализация; управление поведением партнера - контроль, коррекция, оценка действий партнера; умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.

3. Приемы формирования и развития УУД на уроках математики

Для формирования и развития личностных УУД предлагаются следующие приемы: участие в проектах, выбор темы, распределение ролей в группе, определение своего вклада в коллективную работу, выполнение творческих заданий, заданий нравственно-этического характера.

Учащиеся 5-6 классов выполняют следующие проекты:

• Сочинение на тему «Для чего мне нужна математика?», «Математика в профессии моих родителей». [1]

• Диаграммы. Изучение увлечений класса.

• Симметрия. Рисунки, обладающие симметрией. [1]

• Создание рекламы. [2 с.40]

• Создание рисунков по координатам. [1]

• Составление задач по темам «Проценты» (Урок на сайте ИРО), «Задачи на дроби» (Ссылка на Gmail)

Использование заданий творческого характера: «представь, что ты…»Учитель организует групповую работу «Решение задач с процентами». Он предлагает совершить виртуальные экскурсии в учреждения нашего города, где можно встретиться с задачами на проценты. Каждая группа получает свое задание. [2 с.39]

Использование заданий нравственно-этического характера.

Устный счет с использованием истории родного города развивает осознание себя гражданином России, любовь к родному краю.

Примеры заданий.

Важнейшими средствами формирования регулятивных УУД являются действия самоконтроля и самооценки, под которыми понимается умение учащихся самостоятельно проконтролировать и оценить не только результаты собственной деятельности, но и её ход, эффективность. Без этих двух ведущих учебных действий школьник не сможет определить дефицит своих способностей (границу знания и незнания), не сможет поставить перед собой учебную задачу, а, значит, и решить её. Поэтому одной из важнейших задач учителя является формирование в ученике средств самоконтроля и оценки.

Сформировать у учеников навыки самоконтроля и самооценки помогают различные приёмы и способы: итоговая рефлексия в конце каждого урока [3 с.142], различные рефлексивные таблицы, листы самооценки, задания «Найди ошибки» [2 с.37]

Листы самооценки по теме «Действия с рациональными числами».

Умею

Не умею

Хочу научиться

Сложение двух отрицательных чисел

Сложение чисел с разными знаками

самооценка

взаимооценка

оценка учителя

Сложение

Вычитание

Умножение

деление

Другой важной особенностью является понимание и принятие ребенком учебной задачи «я это узнаю, пойму, решу». Как субъект деятельности ребенок сам осуществляет:

А) целеполагание (чего я хочу достичь?):

Б) планирование (как я буду это делать?):

В) оценивать результат деятельности (достиг ли цели? На каком уровне владею материалом?).

В ходе деятельности ученик овладевает общим принципами решения задач, ищет и строит основание этих действий, т.е. закономерности.

Задание. Группа, состоящая из 20 человек и имеющая в наличии некоторую сумму, отправляется в путешествие в город Сочи. Требуется

• выбрать оптимальный вид транспорта

• составить экскурсионную программу на июнь месяц.

Учащимся выдаются буклеты с тарифами на проезд и бензин, экскурсионную программу, информацию о скидках и акциях, карту железнодорожных и автомобильных дорог.

В конце урока учащиеся заполняют рефлексивный лист.

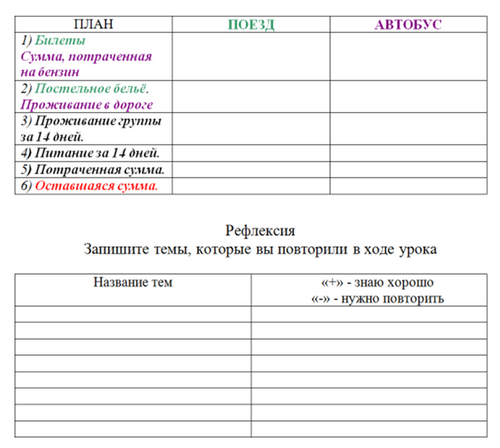
Также эффективны следующие приемы: создание проблемных ситуаций, использование текстов и заданий для открытия нового (что объединяет …, в чем различие…, что для этого нужно сделать…, определи тему урока)

Для формирования познавательных УУД на уроке используются следующие задания: «Дай определение», «Соотнеси», «Сравни», «Сделай вывод о», «Докажите, что», «Объясните, почему», «Предположите, что будет», «К чему может привести, каковы последствия» и т.п.

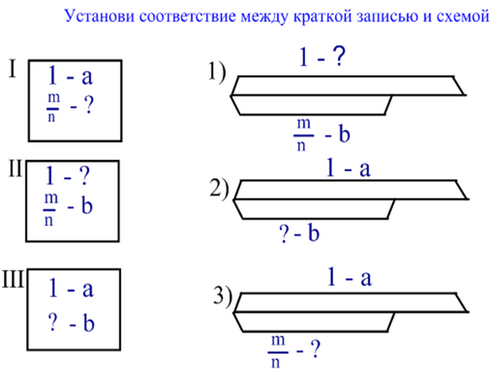
Предметные умения: составлять схемы и краткую запись при решении основных видов задач на части.

Познавательные: выявлять существенные и несуще-ственные признаки объектов познавательной деятельности, преобра-зовывать знаки и символы для решения учебных и познавательных задач

Регулятивные: принимать и сохранять учебную задачу.

Использование заданий: «Составь сравнительную таблицу», «Изобрази схематически», «Составь модель», «Объясни схему», «Опиши рисунок», и т.п.

Например, решение задач практического характера на этапе комплексного применения знаний и умений по теме «Проценты»

Предметные умения: отрабатываем умения применять понятие процента и методы решения задач на части и проценты для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчётах, анализировать текст задачи и моделировать условие

Познавательные: осуществлять смысловое чтение и перевод задачной ситуации на язык математики, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач

Регулятивные: самостоятельно планировать пути достижения целей познавательной деятельности, корректировать свои действия в соответствии с изменяющейся задачной ситуацией.

Для развития коммуникативных УУД очень важны парные и групповые формы организации познавательной деятельности.

Например, учитель организует групповую работу «Решение задач на дроби». Каждая группа получает свое задание. Сначала решают индивидуально, а затем обсуждают решение в группах, анализируют, сравнивают способы решения, готовят выступление. По одному человеку от группы представляют свое решение и говорят о трудностях, возникших в ходе обсуждения. При общем обсуждении, на экране демонстрируется текст задачи, решение на ватмане вывешивается на доске. Учащиеся из других групп читают условие задачи, проверяют ход решения и прикидывают, возможен ли такой ответ, задают вопросы. Это позволяет включить в работу всех учеников класса.

При таком подходе у учащихся формируются умения самостоятельно организовывать взаимодействие в группе, слушать и слышать других; умение с достаточной полнотой излагать свою точку зрения, планировать учебное сотрудничество с учителем и сверстниками.

Проект «Математическое лото по теме «Решение уравнений»

1 этап. Учащиеся дома составляют 10 уравнений: обязательно наличие скобок, подобных слагаемых, дробных чисел. А на отдельном листочке записывают их решение.

2 этап. На уроке учащиеся обмениваются карточками и решают уравнения, составленные партнером.

3 этап. Обсуждают в парах решения, анализируют сложность уравнений, соответствие требованиям.

4 этап. Дома устраняют недостатки и оформляют в виде карточек лото.

Таким образом, мы предложили наиболее интересные и эффективные приемы, которые может использовать учитель при моделировании урока математики с точки зрения формирований УУД. Эти наработки могут быть хорошей основой для зарождения мысли о приемах формирования УУД у коллег - учителей математики. Однако все вышеперечисленные приемы, являются универсальными и могут быть использованы учителем для конструирования урока в рамках любого предмета.

4.Эффективность использования приемов для формирования УУД

Для определения эффективности проанализируем результаты деятельности обучающихся по математике.

1. Средний балл по математике

А

Б

2012-2013, 4 класс

4,32

4,32

2013-2014, 5 класс

4,33

4,28

2014-2015, 6 класс

4,39

4,36

2. Достижения обучающихся по результатам внутренней системы оценки качества образования в образовательной организации.

класс

учитель

Пред-мет

Учащих-ся в классе

сдавали экзамен

Средний балл

«5» и «4»

Процент по классу

Процент по ОУ

5а

Чаузова НС

матем

24

24

4,38

20

83%

80%

5б

Чаузова НС

матем

25

25

4,44

20

80%

5в

матем

25

24

4,25

19

79%

класс

учитель

Пред-мет

Учащих-ся в классе

сдавали экзамен

Средний балл

«5» и «4»

Процент по классу

Процент по ОУ

6а

Чаузова НС

матем

23

23

4,1

20

87%

84%

6б

Чаузова НС

матем

25

25

4,4

21

84%

6в

матем

24

21

3,9

17

81%

3. Увеличение удельного веса обучающихся, принимающих участие в олимпиадах и конкурсах по предмету

Предмет

Формы внеурочной

деятельности

Учебный

год

Классы

Кол-во

учащихся

Охвачены внеурочной деятельностью

Кол-во

учащихся

Процент

Школьный этап олимпиады

2013-2014

5а,5б

49

49

100

2014-2015

6а,6б

48

48

100

Муниципальный этап олимпиады

2013-2014

5а,5б

49

2

4

2014-2015

6а,6б

48

5

10

Кенгуру

2013-2014

5а,5б

49

29

59

2014-2015

6а,6б

48

30

63

Математическое домино

2013-2014

5а,5б

49

11

22

2014-2015

6а,6б

48

15

31

Слон

2013-2014

5а,5б

49

13

27

2014-2015

6а,6б

48

15

31

Совенок

2013-2014

5а,5б

49

10

20

2014-2015

6а,6б

48

7

15

Другие конкурсы (в том числе дистанционные)

2013-2014

5а,5б

49

20

20

2014-2015

6а,6б

48

55

56

4. Достижения обучающихся на предметных олимпиадах

Городская олимпиада по математике

2013-2014 - 5 класс

• Островская Амина-победитель

2014-2015 - 6 класс

• Островская Амина-призер

• Якимов Владимир - призер

• Мальцев Павел - призер

5. Достижения обучающихся в иных конкурсных мероприятиях по предмету (в том числе дистанционных)

Игра «Математическое домино»

2013-2014 - 5 класс

Степанова Анита - Похвальная грамота I степени, Островская Амина - Похвальная грамота II степени, Сычугов Иван - Похвальная грамота II степени, Штин Анастасия - Похвальная грамота II степени

2014-2015 - 6 класс

Островская Амина - диплом I степени, Степанова Анита, Ездаков Егор, Мальцев Павел - Похвальная грамота I степени, Власова Евгения - Похвальная грамота II степени

Международный конкурс-игра по математике «Слон»

2013-2014 - 5 класс

Евдокимова Кира, 5 класс - III место

2014-2015 - 6 класс

Евдокимова Кира, 6 класс - Лауреат

Международный математический конкурс-игра «Кенгуру»

2013-2014 - 5 класс

Якимов Вова - Похвальный отзыв

2014-2015 - 6 класс

Ездаков Егор - Победитель, Якимов Вова - призер, 3 чел- Похвальный отзыв

VI Всероссийская дистанционная олимпиада по математике «Вот задачка»

2013-2014 - 5 класс

Федосеева Настя, Куличик Алина, Мальцев Павел, Евдокимова Кира - победители

2014-2015 - 6 класс

Якимов Вова - Диплом III степени, Машкина Настя - Диплом I степени

Школьные дни. Осенняя сессия.

2014-2015 - 6 класс

Рылова Анастасия, Евдокимова Кира, Куличик Алина, Сухова Ульяна, Медведицына Надя, Штин Анастасия - лауреаты

Совенок

2013-2014 - 5 класс

10 человек - лауреаты первого тура

2014-2015 - 6 класс

Ездаков Егор, Мальцев Павел, Машкина Анастасия - победители первого тура, Островская Амина- призер первого тура. Якимов Вова, Федосеева Настя, Булдаков Дима- лауреаты первого тура

II Всероссийский конкурс «Математические головоломки»

2014-2015 - 6 класс

Машкина Анастасия - 3 место, Якимов Владимир - 3 место .

I Всероссийский марафон «Веселая математика»

2014-2015 - 6 класс

Островская Амина - 2 место, Якимов Владимир - 3 место

Занимательная математика

2014-2015 - 6 класс

Островская Амина - победитель

Математика без границ

2014-2015 - 6 класс

Островская Амина - 2 место, Степанова Анита - 3 место

Эрудит

2014-2015 - 6 класс

Островская Амина - победитель, Ездаков Егор - призер

Библиографический список

1. Личный сайт учителя - режим доступа свободный

2. Приемы формирования универсальных учебных действий на уроках математики Ходырев А.П., Соколова Н.В. Управление качеством образования на основе образова-тельных потребностей и интересов обучающихся: опыт реализации ФГОС ООО: сборник материалов/ А.П.Ходырев, Н.В.Соколова- Киров: ООО «Издательство «Радуга-ПРЕСС», 2015- С.36-41. - ISBN 978-5-9906357-1-1.

3. Технологическая карта учебного занятия «Решение практико-ориентированных задач с процентами Урок математики в основной школе: традиции и новые требования к математическому образованию в условиях реализации ФГОС ООО: сборник материалов межрегиональной научно-практической конференции/ Т.В. Машарова, Е.В. Измайлова и др.:ИРО Кировской области. - Киров:ООО «Типография «Старая Вятка», 2014г.-146 с. -

ISBN 978-5-91061-412-7.