- Учителю
- Пособие по текстовым задачам в помощь учителям математики 5-11 классов
Пособие по текстовым задачам в помощь учителям математики 5-11 классов
Особенности методики обучения
решению текстовых задач
Введение 2
Глава I. Психолого-педагогические особенности при обучении
решению задач
-
Понятие «текстовая задача». Задача и её функции 3
-
Сущность и структура решения текстовой задачи 7
-
Классификация текстовых задач 11
1.4. Задачи в истории математического образования в России 15
1.5. Психологические особенности современных детей 17
1.7. Педагогические основы в обучении решению задач 20
Глава II. Методика обучения учащихся решению
текстовых задач арифметическим способом.
2.1. Знания, умения учащихся по решению текстовых задач по
окончании начальной школы. 23
2.2. Планирование работы учителя по обучению учащихся решению
текстовых задач арифметическим способом
2.3. Организация работы учителя на каждом этапе решения задачи
2.3.1 Организация работы учителя над условием задачи
2.3.2. Организация работы учителя по составлению плана решения
2.3.3. Реализация плана решения
2.3.4. Анализ найденного решения и работа по поиску других
вариантов решения
2.4. Формирование приёмов решения задач «на процессы» 31
2.4.1. Формирование понятия о времени протекания процесса
2.4.2 Формирование понятий о скорости протекания процесса
и его продукте (результате)
2.4.3. Формирование понятия совместного действия
2.5. Составление задач учащимися 35
2.6 Примеры решения задач арифметическим способом 36
Глава III. Решение текстовых задач в старшей школе
3.1 Задачи на движение 44
3.2 Задачи на производительность 56
3.3 Задачи на проценты 59
3.4 Задачи на смеси и сплавы 61
Заключение 68
Библиография 70
Введение
Важнейшим видом учебной деятельности, в процессе которой усваивается система математических знаний, умений и навыков, является решение задач. Именно задачи являются тем средством, которое в значительной степени направляет и стимулирует учебно-познавательную активность учащихся. Задачи формируют систему знаний, творческое мышление учащихся, способствуют развитию интеллекта и выполняют познавательную роль в обучении.
Решение задач является важнейшим средством формирования у школьников системы основных математических знаний, умений и навыков, ведущей формой деятельности учащихся в процессе изучения математики, одним из основных средств их математического развития. Разработкой методики обучения решению текстовых задач занимались такие учёные, как Ю.М.Колягин, Д.Пойа, А.А.Столяр и другие.
В последние годы самые сильные отрицательные эмоции у учащихся на уроках математики вызывает задание решить задачу. Примерно половина из них на контрольной работе или экзамене даже не приступает к решению текстовых задач. Почему так происходит? Зачем надо обучать детей решению текстовых задач и КАК это делать? Эти и другие подобные вопросы все чаще возникают в современной школе. Именно поэтому эта проблема является одной из самых актуальных на сегодняшний день.
Не прекращаются поиски эффективной методики обучения решению текстовых задач в общеобразовательной школе. Решение задач в математическом образовании занимает огромное место.
В пособии будут выделены основные трудности, которые возникают при решении задач.
Первая глава посвящена психологическим особенностям современных учащихся, дидактическим принципам обучения. В ней также даются краткие сведения из истории развития методов обучения текстовым задачам
Во второй главе рассказывается методике решения задач арифметическим способом.
В третий главе рассматриваются основные типы задач, встречающиеся в старшей школе.
В заключении приводится список литературы, полезной при изучении текстовых задач.
Глава I.
Психолого-педагогические особенности
при обучении решению задач
1.1. Понятие «текстовая задача». Задача и ее функции
Обучение решению задач учащимися рассматривается как один из основных методов обучения математике. Процесс решения задач, как сложный аналитико-синтетический процесс, тесно связан с формированием таких приемов мышления, как анализ, синтез, обобщение, абстрагирование и т.д. Решение текстовых задач, как и решение вообще математических задач, воспитывает волю, приучает к систематическому умственному труду, к самоконтролю, развивает сообразительность. В процессе решения текстовых задач у учащихся формируются умения и навыки моделирования реальных объектов и явлений.
Решение задач формирует у учащихся умение планировать свою деятельность, внимательно воспринимать учебную информацию, мотивировать каждый шаг деятельности, рационально оформлять результаты своих действий, осуществлять самоконтроль и пр.
В методике обучения решению задач выделяют четыре их основных функции:
-
Обучающая функция задач направлена на формирование у учащихся системы математических знаний, умений и навыков в процессе их усвоения.
-
Воспитывающая функция задач направлена на воспитание у учащихся интереса к предмету, навыков учебного труда.
-
Развивающая функция задач направлена на развитие мышления учащихся, на формирование у них приемов умственной деятельности.
-
Контролирующая функция задач направлена на определение уровня усвоения учащимися учебного материала, способности их к самостоятельному изучению школьного курса математики, уровня развития и сформированности познавательных интересов школьников.
Функции задач в обучении взаимосвязаны, однако в каждом конкретном случае выделяется и реализуется ведущая функция задачи в соответствии с целевой установкой ее применения.
Умение решать задачи не находится в прямой зависимости от числа решенных задач, поэтому в психолого-дидактических и методических исследованиях отдается предпочтение приемам формирования общих подходов к задаче как объекту ее изучения, ее анализу.
Решению текстовых задач уделяется огромное внимание. Связано это с тем, что такие задачи часто являются не только средством формирования многих математических понятий, но и главное - средством формирования умений строить математические модели реальных явлений, а также средством развития мышления детей.
Существуют различные методические подходы к обучению детей решению текстовых задач. Но какую бы методику обучения не выбрал учитель, ему надо знать, как построены такие задачи, и уметь их решать, прежде всего, арифметическими способами.
Решение задач - это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придется работать, те инструменты, с помощью которых выполняется эта работа.
Значит, для того, чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких основных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Итак, что же такое задача? Любая текстовая задача представляет собой описание какого-либо явления (ситуации, процесса). С этой точки зрения текстовая задача есть словесная модель явления (ситуации, процесса). И как в любой модели в текстовой задаче описывается не все явление в целом, а лишь некоторые его стороны, главным образом, его количественные характеристики.
Рассмотрим, например, такую задачу: «Автомобиль выехал из пункта А со скоростью 60 км/ч. Через 2 ч вслед за ним выехал второй автомобиль со скоростью 90 км/ч. На каком расстоянии от А второй автомобиль догонит первый?» В задаче описывается движение двух автомобилей. Как известно, любое движение характеризуется двумя величинами: пройденным расстоянием, скоростью и временем движения. В данной задаче известны скорости первого и второго автомобилей (60 км/ч и 90 км/ч), известно, что они прошли одно и то же расстояние от пункта А до места встречи, количественную характеристику которого и надо найти. Кроме того, известно, что первый автомобиль был в пути на 2 ч больше, чем второй. Обобщая, можно сказать, что текстовая задача есть описание на естественном языке некоторого явления (ситуации, процесса) с требованием дать количественную характеристику какого-либо явления, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения.
Чтобы выявить, как построена текстовая задача, рассмотрим следующий пример: «Свитер, шапку и шарф связали из 1 кг 200 г шерсти. На шарф потребовалось на 100 г шерсти больше, чем на шапку, и на 400 г меньше, чем на свитер. Сколько шерсти израсходовали на каждую вещь?»
В задаче речь идет о свитере, шапке и шарфе. Это объекты задачи. Относительно этих объектов имеются определенные утверждения и вопросы.
Утверждения:
1. Свитер, шапка и шарф связаны из 1200 г шерсти.
2. На шарф израсходовали на 100 г больше, чем на шапку.
3. На шапку израсходовали на 400 г меньше, чем на свитер.
Вопросы:
1. Сколько шерсти израсходовали на свитер?
2. Сколько шерсти израсходовали на шапку?
3. Сколько шерсти израсходовали на шарф?
Утверждения задачи называют условиями. В задаче обычно не одно условие, а несколько элементарных условий. Они представляют собой количественные или качественные характеристики объектов задачи и отношений между ними. Вопросов в задаче может быть несколько. Они могут быть сформулированы как в вопросительной, так и утвердительной форме. Условия и вопросы взаимосвязаны.
По отношению между условиями и вопросами различают:
а) определенные задачи - в них заданных условий столько, сколько необходимо и достаточно для ответа на вопросы;
б) недоопределенные задачи - в них условий недостаточно для получения ответа;
в) переопределенные задачи - в них имеются лишние условия.
Недоопределенные задачи считают задачи с недостающими данными, а переопределенные - задачами с избыточными данными.
Например, задача «Возле дома росло 5 яблонь, 2 вишни и 3 березы. Сколько фруктовых деревьев росло возле дома?» является переопределенной, так как содержит лишнее условие. Задача «Из зала вынесли 12 стульев, а потом еще 5. Сколько стульев осталось в зале?» является недоопределенной - в ней недостаточно условий, чтобы ответить на поставленный вопрос. Чтобы понять, какова структура задачи, надо выявить ее условия и требования, отбросив все лишнее, второстепенное, не влияющее на ее структуру. Иными словами, надо построить высказывательную модель задачи. Систему взаимосвязанных условий и требований называют высказывательной моделью задачи.
Чтобы получить эту модель, надо текст задачи развернуть (сделать это можно письменно или устно), так как текст задачи, как правило, дается в сокращенном, свернутом виде. Для этого можно перефразировать задачу, построить ее графическую модель, ввести какие-либо обозначения и т.д. Анализ задачи и вычисление ее условий и требований можно производить с разной глубиной. Глубина анализа зависит от того, знакомы ли мы с видом задач, к которому принадлежит заданная, и знакомы ли с общим способом решения этих задач. Если да, то нам достаточен простейший анализ, сводящийся к установлению вида данной задачи; если нет, то для нахождения решения задачи нужен более глубокий анализ.
Рассмотрим пример.
Катер прошел 20 км по течению реки и 20 км против течения реки. Затратит ли он на весь путь больше времени, чем ему требуется на прохождение 40 км в стоячей воде, меньше или столько же?
Первичный анализ этой задачи позволяет вычленить такие условия:
1) катер прошел 20 км по течению реки;
2) катер прошел 20 км против течения реки;
3) катер прошел 40 км в стоячей воде.
Но, сопоставив эти условия с требованием задачи: узнать больше, меньше или столько же времени затратил катер на первый и второй пути вместе по сравнению с третьим, мы обнаруживаем недостаточность произведенного анализа. Эта недостаточность проявляется хотя бы в том, что в условиях ничего не говорится о времени, а требование задачи сводится к сравнению промежутков времени. Поэтому нужно продолжить анализ. Для этого вдумаемся в требование задачи. Надо сравнить время движения катера по реке с движением катера в стоячей воде. От чего зависит это время? Очевидно, от собственной скорости катера, от скорости течения реки и, конечно, пройденных расстояний. Но если пройденные расстояния в формулировке задачи даны, то о скорости катера и реки даже не упоминается. Как же быть? В таких случаях эти величины, без которых решение задачи невозможно, принимаются за неопределенные параметры. Положим, например, что собственная скорость катера равна vс км/ч. Теперь мы можем вычленить такие условия:
1) собственная скорость катера vс км/ч;
2) скорость течения реки vт км/ч;
3) катер проплыл 20 км по течению реки;
4) катер проплыл 20 км против течения реки;
5) на весь путь туда и обратно по реке катер затратил t1 ч;
6) в стоячей воде катер проплыл 40 км;
7) на этот путь катер затратил t2 ч.
Требование задачи: сравнить t1 и t2 и установить, равны ли они или нет, а если нет, то какое время больше.
Результаты предварительного анализа задач надо как-то зафиксировать, записать. Та словесная, описательная форма записи, которую мы использовали выше, конечно, малоудобна. Надо найти более удобную, более компактную и в то же время достаточно наглядную форму записи результатов анализа задач. Такой формой является схематическая запись задачи. Заметим, что не для всякой задачи надо делать схематическую запись. Для задач, которые записаны на символическом языке (с помощью общепринятых обозначений и символов), схематическая запись не нужна.
Первой отличительной особенностью схематической записи задач является широкое использование в ней разного рода обозначений, символов, букв, рисунков, чертежей и т.д.
Второй особенностью является то, что в ней четко выделены все условия и требования задачи, а в записи каждого условия указаны объекты и их характеристики, наконец, в схематической записи фиксируется лишь только то, что необходимо для решения задачи; все другие подробности, имеющиеся в задаче, при схематической записи отбрасываются.
На практике используется много разных видов схематической записи задач. Покажем на примерах.
С одного участка собрали 1440 ц. пшеницы, а с другого, площадь которого на 12 га меньше, - 1080 ц.. Найти площадь первого участка, если известно, что на первом участке собирали пшеницы с каждого гектара на 2 ц больше, чем на втором.
Анализ задачи показывает, что в ней рассматривается сбор урожая пшеницы с двух участков, при этом этот сбор характеризуется тремя величинами: массой собранной пшеницы, площадью участка и урожаем с одного гектара. Исходя из этого, составим таблицу для схематической записи условий и требований задачи. Неизвестные величины, встречающиеся в задаче, запишем в таблице буквами, притом искомое обозначим буквой х:
Участки
Масса собранной пшеницы, ц
Урожай с 1 га, ц
Площадь участка, га
Первый
1440
y+2
х
Второй
1080
y
х - 12
В этой схематической записи выделены все условия, их объекты и характеристики. Указано и требование задачи: найти площадь первого участка. В то же время эта запись очень компактная, наглядная и полностью заменяет саму формулировку задачи.
Решим эту задачу.
1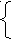
 440 : (y+2) = x
440 : (y+2) = x
1080 : y = x - 12
y2 - 28y + 180 = 0
y1 = 10, y2 = 18 (урожай с 1 га второго участка)
Ответ: площадь первого участка 120 га или 72 га
Обратите внимание, что оба значения подходят по смыслу к условию задачи.
Довольно часто удобно составлять схематическую запись не для всей задачи, а лишь для какой-либо ее части, чтобы более наглядно представлять описываемую в задаче ситуацию, а также чтобы в решении оперировать теми обозначениями, которые вводятся в этой частичной схематической записи. В этих случаях используются разного рода графические схемы.
1.2 Сущность и структура решения текстовых задач
Что значит решить математическую задачу?
Термином «решение задачи» обозначают понятия:
1) решением задачи называют результат, т.е. ответ на требование задачи;
2) решением задачи называют процесс нахождения этого результата, причем этот процесс рассматривают двояко: и как метод нахождения результат и как последовательность тех действий, которые выполняет решающий, применяя тот или иной метод (т.е. в данном случае под решением задачи понимается вид деятельности человека, решающего задачу).
Решить математическую задачу - это значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения), получаем то, что требуется, - ее ответ.
Если под процессом решения задач понимать процесс, начинающийся с момента получения задачи до момента полного завершения ее решения, то, очевидно, что этот процесс состоит не только из изложения уже найденного решения, а из ряда этапов, одним их которых и является изложение решения. Из каких же этапов состоит процесс решения задачи? Очевидно, получив задачу, первое, что нужно сделать, - это разобраться в том, что это за задача, каковы ее условия, в чем состоят ее требования, т.е. провести первичный анализ задачи. Этот анализ и составляет первый этап процесса решения задачи.
В ряде случаев этот анализ надо как-то оформить, записать. Для этого используются разного рода схематические записи задач, построение которых составляет второй этап процесса решения.
Анализ задачи и построение ее схематической записи необходимы главным образом для того, чтобы найти способ решения данной задачи. Поиск решения составляет третий этап процесса решения.
Когда способ решения задачи найден, его нужно осуществить, - это будет уже четвертый этап процесса решения - этап осуществления (изложения) решения.
После того, как решение осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения.
При решении многих задач, кроме проверки, необходимо еще произвести исследование задачи, а именно установить, при каких условиях задача имеет и при том сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения.
Убедившись в правильности решения и, если нужно, произведя исследование задачи, необходимо четко сформулировать ответ задачи, - это будет седьмой этап процесса решения.
Наконец, в учебных и познавательных целях полезно также провести анализ выполненного решения, в частичности установить, нет ли другого, более рационального способа решения, нельзя ли задачу обобщить, какие выводы можно сделать из этого решения и т.т. Все это составляет последний, конечно, не обязательный, восьмой этап решения.
Итак, весь процесс решения задачи можно разделить на восемь этапов:
-
анализ задачи;
-
схематическая запись задачи;
-
поиск способа решения задачи;
-
осуществление решения задачи;
-
проверка решения задачи;
-
исследование задачи;
-
формулирование ответа задачи;
-
анализ решения задачи.
Приведенная схема дает лишь общее представление о процессе решения задач как о сложном и многоплановом процессе. Приведем пример решения задачи, показав конкретно этот процесс.
Задача.
Лодка прошла по течению реки расстояние между двумя пристанями за 6 ч, а обратный путь она совершила за 8 ч. За сколько времени пройдет расстояние между пристанями плот, пущенный по течению реки?
1. Анализ задачи.
В задаче речь идет о двух объектах: лодка и плот. Лодка имеет какую-то собственную скорость, а река, по которой плывет и лодка, и плот, имеет определенную скорость течения. Именно поэтому лодка совершает путь между пристанями по течению реки за меньшее время (6 ч), чем против течения (8 ч). Но эти скорости (собственная скорость лодки и скорость течения реки) в задаче не даны (они неизвестны), так же как неизвестно расстояние между пристанями. Однако требуется найти не эти неизвестные скорости и расстояния, а время, за которое плот проплывет неизвестное расстояние между пристанями.
2. Схематическая запись задачи.
3. Поиск способа решения задачи.
Нужно найти время, за которое плот проплывает расстояние между пристанями А и В. Для того чтобы найти это время, надо знать расстояние АВ и скорость течения реки. Оба они неизвестны, поэтому обозначим расстояние АВ буквой S (км), а скорость течения реки примем равной vтеч км/ч. Чтобы связать эти неизвестные с данными задачи (время движения лодки по течению и против течения реки), нужно еще знать собственную скорость лодки. Она тоже неизвестна, положим, что она равна v км/ч. Отсюда естественно возникает план решения, заключающийся в том, чтобы составить систему уравнений относительно введенных неизвестных.
4. Осуществление решения задачи.
Итак, пусть расстояние АВ равно S км, скорость течения реки vтеч км/ч, собственная скорость лодки v км/ч, а искомое время движения плота на пути в S км равно х ч. Тогда скорость лодки по течению реки равна (v + vтеч) км/ч. За 6 ч лодка, идя с этой скоростью, прошла путь АВ в S км. Следовательно,
6 (v + vтеч) = S (1)
Против течения эта лодка идет со скоростью (v - vтеч) км/ч и путь АВ в S км она пройдет за 8 ч, поэтому
8 (v - vтеч) = S (2)
Наконец, плот, плывя со скоростью vтеч км/ч, покрыл расстояние S км за х ч, следовательно,
vтеч х = S (3)
Уравнения (1), (2), (3) образуют систему уравнений относительно неизвестных S, vтеч, v и х. Так как требуется найти лишь х, то остальные неизвестные постараемся исключить.
Для этого из уравнений (1) и (2) найдем:
v + vтеч = S:6, v - vтеч = S:8.
Вычитая из первого уравнения второе, получим:
2 vтеч = S:6 - S:8 , отсюда vтеч = (S:6 - S:8) : 2 vтеч = S : 24
vтеч = S:6 - S:8 , отсюда vтеч = (S:6 - S:8) : 2 vтеч = S : 24
Поставим найденное выражение для vтеч в уравнение (3):
(S : 24): 2 · х = S.
Так как, очевидно, S не равно 0, то можно обе части полученного уравнения разделить на S. Тогда найдем х = 48 часов.
5. Проверка решения.
Итак, мы нашли, что плот проплывет расстояние между пристанями за 48 ч. Для того, чтобы убедиться в правильности решения, достаточно проверить, будут ли равны собственные скорости лодки, найденные двумя способами:
1) от скорости лодки по течению отнять скорость течения реки;
2) к скорости лодки против течения реки прибавить скорость течения реки.
Произведя вычисления, получаем верное равенство.
Значит, задача решена правильно.
6. Исследование задачи.
В данном случае этот этап решения не нужен.
7. Ответ:
Плот проплывет расстояние между пристанями за 48 ч.
8. Анализ решения.
Мы свели решение этой задачи к решению системы трех уравнений с четырьмя неизвестными. Однако найти-то надо было нам лишь одно из этих неизвестных. Поэтому, естественно, возникает мысль, что проведенное решение не самое удачное, хотя и достаточно простое. Можно предложить другое решение.
Зная, что лодка проплыла расстояние АВ по течению реки за 6 ч, а против - за 8 ч, найдем, что в 1 ч лодка, идя по течению, проходит 1/6 часть этого расстояния, а против течения 1/8. Тогда разность между ними (1/6 - 1/8 = 1/24 ) есть удвоенная часть расстояния АВ, проплываемая плотом за 1 ч. Значит. Плот за 1 ч проплывет 1/48 часть расстояния АВ, следовательно, все расстояние АВ он проплывет за 48 ч.
При таком решении не понадобилось составлять систему уравнений. Однако, несомненно, это решение сложнее приведенного выше, хотя бы потому, что не всякий догадается найти разность скоростей лодки по течению и против течения реки. Часто эту разность принимают не за удвоенную часть расстояния АВ, проплываемую плотом за 1 ч, а за скорость плота.
Таким образом, структура процесса решения задачи зависит в первую очередь от характера задачи и, конечно, от того, какими знаниями и умениями обладает решающий задачу.
Приведенная выше схема решения задач является лишь примерной. При фактическом решении указанные там этапы обычно не отделены друг от друга, а переплетаются между собой. Так, в процессе анализа задачи обычно производится и поиск решения. При этом полный план решения устанавливается не до осуществления решения, а в процессе. Тогда поиск решения ограничивается лишь нахождением идеи решения. Порядок этапов также иногда может меняться.
Из указанных восьми этапов пять являются обязательными, и они имеются (в том или ином виде) в процессе решения любой задачи. Это этапы анализа задачи, поиска способа ее решения, осуществления решения, проверки решения и формулирования ответа. Остальные три этапа (схематическая запись задачи, исследование задачи и заключительный анализ решения) являются не обязательными и в процессе решения многих задач не имеются.
1.3 Классификация задач
Говоря о классификации задач, необходимо определить, из каких же компонентов состоит задача и на какие этапы можно разделить процесс решения задачи.
Процесс решения задачи в методике преподавания математики принято делить на четыре основных типа:
1. Осмысление условия задачи.
На этом этапе учащиеся должны осознавать условие и требование задачи, разработать отдельные элементы условия, произвести поиск необходимой информации в своей памяти, соотнести с этой информацией условие и заключение задачи и т.д.
Процесс решения задачи
2. Составление плана решения.
На этом этапе учащийся должен провести целенаправленные пробы различных сочетаний из данных и искомых, подвести задачу под известный тип, выбрать приемлемые методы, наметить план решения и т.д.
3. Осуществление плана решения.
Учащиеся практически реализуют план решения, с одновременной его корректировкой через соотношение с условием и выбранным базисом, выбирают способ оформления решения, оформляют решение и т.д.
4. Изучение найденного решения.
На этом этапе фиксируется конечный результат решения задачи, проводится его анализ, исследуются особые и частные случаи и т.д.
В педагогической литературе существуют различные подходы к классификации задач (по Ю.М. Колягину, Г.В. Дорофееву и др.).
Рассмотрим некоторые их них.
По количеству неизвестных компонентов в структуре задачи Ю.М. Колягин выделяет следующие задачи:
а) Обучающие задачи (их структура содержит один неизвестный компонент).
Эти задачи он в свою очередь подразделяет на:
-
задачи с неизвестными начальными состояниями (например: известны корни приведенного квадратного уравнения, найти само уравнение).
-
задачи с неизвестной теоретической базой (например: найти ошибку в решении).
-
задачи с неизвестным алгоритмом решения (например: в записи 1*2*3*4*5 заменить звездочки значками действий и расставить скобки так, чтобы получалось выражение, значение которого равно 10).
-
задачи с неизвестным конечным состоянием (например: найти значение какого-либо выражения).
б) Задачи поискового характера (т.е. те задачи, в структуре которых неизвестны два компонента).
в) Проблемные задачи (задачи с тремя неизвестными компонентами).
По отношению к теории выделяют стандартные и нестандартные задачи.
Примеры стандартных задач:
1. Первый мотоциклист за 1,3 часа проехал на 36,6 км больше, чем второй за 1,1 часа. Найдите скорость каждого, если скорость второго мотоциклиста на 26 км/ч меньше скорости первого.
2. Для детей 11 лет наиболее полноценным является питание, если пища содержит 11% животных белков, 6% растительных белков, 16% животного жира, 2% растительного жира и 65% углеводов. По этим данным построить круговую диаграмму.
Примеры нестандартных задач:
1. У Змея Горыныча 1983 головы. Иванушка может отрубить ему одним ударом меча 33, 21, 17 или 1 голову. При этом у Змея Горыныча вырастают соответственно 85, 0, 14, 578 голов (если отрублены все головы, но новые не вырастают). Сможет ли Иванушка победить Змея?
2. Три товарища - Иван, Дмитрий, Степан преподают различные предметы (химию, биологию, физику) в школах Москвы, Санкт-Петербурга и Киева. Известно, что Иван преподает не в Москве, а Дмитрий не в Санкт-Петербурге. Москвич преподает не физику, а тот, кто работает в Санкт-Петербурге, преподает химию, Дмитрий преподает не биологию. Какой предмет и в каком городе преподает каждый из товарищей?
Соотнесение задач с каждым компонентом учебно-познавательной деятельности приводит к такой классификации: задачи, стимулирующие учебно-познавательную деятельность школьников; организующие и осуществляющие учебно-познавательную деятельность; задачи, в процессе выполнения которых осуществляется контроль и самоконтроль эффективности учебно-познавательной деятельности.
По своему математическому содержанию, соответствующему специфике той или иной математической дисциплины, задачи подразделяются на арифметические, алгебраические, аналитические, геометрические.
По характеру требований выделяют следующие группы задач:
а) задачи на вычисление;
б) задачи на построение;
в) задачи на доказательство;
г) задачи текстовые;
д) задачи комбинаторного характера.
Пример задачи на вычисление:
Среди людей 3% левшей и 7% людей, не подверженных морской болезни. В школе учится 1200 учащихся. Сколько среди них может быть левшей и не подверженных морской болезни?
Пример задачи на построение:
Построить равнобедренный треугольник по боковой стороне и углу при основании.
Пример задачи на доказательство:
Докажите, что в любом треугольнике сумма трех высот меньше периметра треугольника.
Пример задачи текстовой:
За 9 часов по течению реки теплоход проходит тот же путь, что за 11 часов против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.
Пример задачи комбинированного характера:
Постройте треугольник по двум сторонам и углу между ними и вычислите его площадь.
Г.В. Дорофеев делит задачи на два типа:
а) задачи, в которых речь идет о некоторой реальной, а более точно, о реализованной жизненной ситуации;
б) задачи потенциального характера, в которых жизненную ситуацию требуется сконструировать, смоделировать, выяснить условия, при которых она реализована.
По содержанию задачи классифицируют на: «задачи на движение», «задачи на части», «задачи на проценты» и т.д. внутри каждого типа в зависимости от логической структуры задачи разделяют виды задач. Так, например, различают вид задач на встречное движение в одну сторону и движение в противоположные стороны, различают задачи на нахождение части числа и нахождение числа по заданной его части, нахождение соотношения чисел, различают задачи на нахождение нескольких процентов числа, нахождение числа по его проценту, нахождение процентного отношения или выражение частного в процентах.
Для учащихся 5-6 классов согласно новым ФГОС Шевкин А.В. предлагает следующую классификацию задач
1. Натуральные числа
1.1. Сложение и вычитание натуральных чисел
Задача: Ученик токаря обточил 120 деталей за смену, а токарь на 36 деталей больше. Сколько деталей обточили токарь и его ученик вместе?
1.2. Умножение и деление натуральных чисел
Задача: В первом мотке 42 м проволоки, а во втором в 3 раза больше.
Сколько метров проволоки в двух мотках?
1.3. Задачи «на части»
Задача: При помоле ржи на каждые 3 части муки получается 1 часть отходов. Сколько центнеров ржи смололи, если муки получилось на 36 ц больше, чем отходов?
1.4. Нахождение двух чисел по их сумме и разности
Задача: В двух пачках было 40 тетрадей. Когда из первой пачки взяли 10 тетрадей, то тетрадей в пачках стало поровну. Сколько тетрадей было во второй пачке первоначально?
1.5. Задачи на движение по реке
Задача: Собственная скорость теплохода 27 км/ч, скорость течения реки 3 км/ч. Сколько времени затратит теплоход на путь по течению реки между двумя причалами, если расстояние между ними равно 120 км?
1.6. Задачи на движение
Задача: Два поезда вышли одновременно из одного пункта в противоположных
направлениях. Их скорости 60 км/ч и 70 км/ч. Через сколько часов расстояние между ними будет 260 км?
2. Дроби
2.1. Нахождение части числа и числа по его части
Задача: В драмкружке занимаются 24 девочки и несколько мальчиков. Число мальчиков составляет 3/8 числа девочек. Сколько учащихся занимаются в драмкружке?
2.2. Сложение и вычитание обыкновенных дробей
Задача: Туристы прошли 1/7, потом еще 3/7 всего маршрута. Какую часть маршрута им осталось пройти?
2.3. Умножение и деление обыкновенных дробей
Задача: Столб вкопали в землю на 2/9 его длины. Он возвышается над землей на 1 м 5 см. Определите длину столба.
2.4. Задачи «на бассейны» и другие
Задача: За 1 ч первая труба наполняет 1/3 бассейна, а вторая 1/6 бассейна. Какую часть бассейна наполняют обе трубы за 1 ч совместной работы? За сколько часов наполнится бассейн через обе трубы?
3. Пропорции
3.1. Задачи на прямую и обратную пропорциональность
Задача: Расстояние между городами можно проехать на велосипеде или на мотоцикле. Какова зависимость между временем и скоростью движения?
3.2. Задачи на прямую и обратную пропорциональность для трех и более
величин
Задача: 3 курицы за 3 дня снесли 3 яйца. Сколько яиц снесут 12 кур за 12 дней?
4. Проценты
4.1. Нахождение процентов числа
Задача: Папа вложил 5000 р. в акции своего предприятия и получил 20% дохода. Сколько рублей дохода получил папа?
4.2. Нахождение числа по его процентам
Задача: 60% класса пошли в кино, а остальные 12 человек - на выставку. Сколько учащихся в классе?
4.3. Нахождение процентного отношения
Задача: Из 16 кг свежих груш получили 4 кг сушеных. Какую часть массы свежих груш составляет масса сушеных? Выразите эту часть в процентах. Сколько процентов массы теряется при сушке?
4.4. Сложные задачи на проценты
Задача: Вася прочитал в газете, что за последние 3 месяца цены на продукты питания росли в среднем на 10% за каждый месяц. На сколько процентов выросли цены за 3 месяца?
5. Уравнения
5.1. Решение задач с помощью уравнения
Задача: Ученик рассчитал, что стоимость одной книги составляет 70% имеющихся у него денег, а другой книги - 60%. Если бы у него было еще 18 р., то он смог бы купить обе книги. Сколько денег было у ученика?
5.2. Более сложные задачи, решаемые уравнением
Задача: У мальчика в коллекции было 210 российских марок и 65 иностранных. Когда ему подарили еще 25 марок, то российских марок стало в 3 раза больше, чем иностранных. Сколько российских марок подарили мальчику?
Приведенные классификации позволяют учителю представить себе проблемы, связанные с методикой обучения учащихся решению задач.
1.4. Задачи в истории математического образования в России
С древнейших времен люди сталкивались с необходимостью решения различных практических задач. Приходилось отыскивать способы их решения. Т.о., текстовые задачи изначально были «движущей силой» развития математики. Математические знания были связаны с практическими нуждами людей: летоисчислением, вычислением поголовья и стоимости скота, определением прибыли от урожая и т.д. Древнейшая русская математическая рукопись, сохранившаяся до наших дней, датируется 1136 годом. Автором этой рукописи был новгородский дьякон и «чистолюбец» Кирик. Записки содержат задачи на суммирование прогрессий, связанные с приплодом коров и овец, исчисление количества месяцев, недель и дней, прошедших со дня отворения мира, вычисление размеров Солнца и Луны по астрономическим данным. Измерение земель, военное дело, развивающиеся торговые отношения - все требует прикладных математических знаний.
В XVI - XVII веках в России начинает появляться и распространяться рукописная математическая литература. В основном она предназначалась для купцов, ремесленников, землемеров и носила сугубо практический характер. Материалы в этих математических трудах распределялись по статьям, содержащим указания, как надо поступать при решении тех или иных задач. Правила пояснялись различными примерами и задачами. Рукописи XVI - XVII веков послужили основой для создания учебной литературы XVIII века. Многие задачи перешли в учебники по арифметике и алгебре в XVIII век из старых рукописей, некоторые задачи сохранились до наших дней. Проводимые Петром I реформы государственной, общественной и культурной жизни страны затронули и образование. Для вновь созданных учебных заведений нужны были учебники. В 1703 году был создан учебник математики, автором которого был замечательный педагог-математик Леонтий Филиппович Магницкий, а назывался он «Арифметика, сиречь наука числительная…», прослужившая в качестве школьного учебника почти до середины XVIII века. Задачи, так или иначе, сопровождают человека на протяжении всей его жизни. Целый пласт фольклорного наследия русского народа - это загадки. Но что такое загадка? Это задача в стихах, решение которой требует внимания, сообразительности, логики, а иногда и чисто математических знаний.
Текстовые задачи постоянно привлекают внимание математиков, педагогов и психологов. Теорией задачи в России занимались такие исследователи как В.И. Крупич, Л.М. Фридман и др. В настоящее время задаче уделяется большое внимание как основному средству обучения, как средству контроля знаний, умений и навыков учащихся, как средству гуманизации и гуманитаризации образования.
Первоначально обучение математике велось через обучение решению практических задач. Ученики, подражая учителю, решали задачи на определенное «правило». Аналогично обучали решению задач по одному из первых и самому известному в России учебнику «Арифметика» Л.Ф. Магницкого (1703 год). Следы обучения по правилам находили и в «Арифметике» А.П. Киселева. Но у него правила давались как обобщение подробно разобранных и обоснованных способов решения.
К середине XX века сложилась развитая типология задач, включавшая задачи на части, на нахождение двух чисел по их сумме и разности, по их отношению и сумме (разности), на дроби, на проценты, на совместную работу и пр.
Методика обучения решению задач была разработана достаточно хорошо, но возникали проблемы с ее реализацией на практике. Критики традиционной методики обучения решению задач в то время отличали, что учителя, стремясь ускорить процесс обучения, попросту натаскивали учащихся на решения типовых задач, как бы следуя своим давним предшественникам. Они учили школьников выделять задачи данного типа из массы других и разучивали способы их решения.
Методика и школьная практика нуждались в совершенствовании. Это и предполагалось осуществить в ходе реформы школьного математического образования конца 60-х годов. Тогда считалось, что ранее введение уравнений позволит по-новому организовать обучение решению задач, что учащимся будут раскрыты преимущества алгебраического способа решения задачи перед арифметическим, и в дальнейшем предполагалось предоставить право выбора способа решения задач самими учащимися. Это написано в объяснительной записке к программе по математике для 4 - 5 классов на 1971/72 уч. год. На практике новые идеи не реализовывались потому, что способ решения задачи выбирали не сами учащиеся, а авторы единственного тогда учебника. Традиционных арифметических способов решения задач больше не изучали. В самом начале 4 (теперь 5) класса учащихся ориентировали на решение задач с помощью уравнений. Такое отношение к арифметическим способам решения задач отражало мнение многих методистов и авторов учебников того времени.
Однако роль алгебраического способа решения задач в учебном процессе была явно преувеличена, потому что из школьной практики были удалены арифметические способы их решения. Но практика показывает, что раннее введение этого способа решения задач без достаточной подготовки мышления учащихся не дает большого эффекта. Ведь исторически люди пришли к применению уравнений, обобщая решения задач, в которых приходилось иметь дело с неизвестным числом, называемых словами «куча» и т.п.
Ребенок должен пройти тот же путь - сначала рассуждать о «частях», опираясь на воображаемые действия с конкретными предметами или величинами, и лишь потом подойти к применению уравнения. Ведь у учащихся 5 - 6 классов особенности мышления тяготеют к оперированию наглядными образами, а не абстрактными моделями.
На данном этапе обучения арифметические способы решения задач имеют преимущество перед алгебраическими уже потому, что результат каждого отдельного шага в решении по действиям имеют совершенно наглядное и конкретное истолкование, которое не выходит за рамки опыта учащихся. Не случайно школьники быстрее и лучше усваивают различные приемы рассуждений, которые опираются на воображаемые действия с известными величинами.
Что же мы имеем теперь? Указанные выше недостатки до конца не предопределены. Разница только в том, что типовых задач стало меньше, а опыт мыслительной деятельности школьников - беднее. А дети, как и раньше, все равно выделяют для себя типы задач, чтобы решить их «по образцу».
1.5. Психологические особенности современных детей
Важнейшей является задача развития мышления учащихся. В процессе обучения ребенок оперирует как с самими предметами, так и опосредованно, с символами предметов и отношений между ними. Операции с этими элементами производятся мысленно, и они обратимы, т.е. действие операций может быть сведено на нет применением некоторых обратных операций. В сознании развиваются системы символов, посредством которых ребенок воспринимает мир. Для того чтобы ребенок усвоил некоторые понятия, их следует перевести именно на язык этих внутренних структур. Мышление позволяет учащимся выявлять в сознаваемых объектах не только отдельные их свойства и стороны, что возможно установить с помощью чувств, но и отношения и закономерности связей между этими свойствами и сторонами. Тем самым с помощью мышления он познает общие свойства и отношения, выделяет среди них существенные, главные, определяющие характер объектов. Это позволяет ученика предвидеть результаты наблюдаемых событий, явлений и своих собственных действий, проверяемых в дальнейшем путем эксперимента или наблюдения. Возрастает исследовательская активность, ее широта и разносторонность, происходит развитие умения ставить вопросы как средства самостоятельного мышления. Вся эта огромная работа выполняется с помощью мыслительных операций: сравнения, анализа и синтеза, абстракции, обобщения и конкретизации.
Математическое мышление - это предельно абстрактное, теоретическое мышление, объекты которого лишены всякой вещественности и могут интерпретироваться самым произвольным образом, лишь бы при этом сохранялись заданные между ними отношения. Необходимо уделять внимание восприятию временных и пространственных отношений, указанных в задаче. Учащиеся могут самостоятельно оперировать понятиями: скорость, время, расстояние и т.п. Все это будет успешно реализовываться, если у ученика сформировано произвольное внимание, т.е. внимание, направленное учеником в соответствии с целями и задачами. Это внимание является контролем за совершаемыми действиями.
Первоначально у ребенка образная память, но затем ее значение (образной памяти) уменьшается. Тем не менее, результат запоминания обычно выше при опоре на наглядный материал.
В процессе обучения развивается абстрактно-теоретическое, наглядно-действенное и наглядно-образное виды мышления, при этом они развиваются в тесном взаимодействии друг с другом. Учитывая их взаимодействие, уже давно одним из основных принципов обучения считается принцип наглядности, в соответствии с которым обучение строится на конкретных образах, непосредственно воспринимаемых учащимися. Отвечая на вопрос о психологической функции наглядного материала, включенного в процесс обучения, А.Н. Леонтьев указывает, что она состоит в том, что «он (наглядный материал) служит как бы внешней опорой внутренних действий, совершаемых ребенком под руководством учителя в процессе овладения знаниями».
Общий вывод, к которому приходит А.Н. Леонтьев в исследовании проблемы наглядности в обучении, состоит в том, что место и роль наглядного материала в процессе обучения определяются отношением деятельности учащихся с наглядным материалом к той деятельности, которая составляет суть процесса обучения.
Это означает, что целесообразность использования тех или иных средств наглядности зависит от того, способствует ли деятельность, непосредственной целью которой является освоение этой наглядности, другой деятельности (основной) по овладению учащимися знаниями, ради усвоения которых и используются эти средства наглядности. Если эти две деятельности не связаны между собой, то наглядный материал бесполезен, а иногда даже может играть роль отвлекающего фактора.
Исследуя проблему наглядности, В.В. Давыдов приходит к следующему весьма важному выводу: «… тем, где содержанием обучения выступают внешние свойства вещей, принцип наглядности себя оправдывает. Но там, где содержанием обучения становятся связи и отношения предметов, - там наглядность далеко не достаточна. Здесь … вступает в силу принцип моделирования.». А так как в курсе математики основным содержанием как раз являются разного рода отношения, то, следовательно, основным для этого курса является не принцип наглядности, а принцип моделирования. В чем он состоит? Принцип моделирования не противопоставляется принципу наглядности - он лишь является его высшей ступенью, его развитием и обобщением. При обучении учащиеся должны опираться на наглядность и на чувственные образы. Необходимо давать учащимся схемы, графики для упрочнения этих образов, их изучения.
Но также при решении задач нужно уметь оперировать абстрактными понятиями и рассуждениями, т.е. должно развиваться теоретическое мышление.
Этот возрастной период - период взросления. Развиваются вычислительные и интеллектуально-познавательные способности. Увеличивается стремление к самостоятельной деятельности. Образы, объекты носят более осмысленный характер. Вырабатывается воля достижения цели в обучении. Деятельность становится осмысленной. Поэтому, чтобы у учащихся было стремление к учению, нужно идти чуть впереди их развития, но при этом опираться на принцип доступности, т.е. идти в пределах зоны ближайшего развития. Обучение (тем более решению задач, т.к. у каждого учащегося возникают свои трудности) должно быть личностно-ориентированным (учитывать психику и особенности учащегося).
А чтобы обучение учащихся было успешнее, необходимо учитывать психологические особенности их познавательных процессов.
При возникновении некоторых задач ребенок пытается решить их, реально примеряясь и пробуя, но он же не может решать задачи, как говорится, в уме. Он представляет себе реальную ситуацию и как бы действует в ней в своем воображении. Такое мышление, в котором решение задачи происходит в результате внутренних действий с образами, называется наглядно-образным. Конечно, они могут мыслить логически, но следует помнить, что этот возраст склонен к обучению, опирающемуся на наглядность. Затем у ребенка все большее значение начинает приобретать теоретическое мышление, способность устанавливать максимальное количество смысловых связей в окружающем мире. В возрасте 11 - 12 лет у подростка вырабатывается формальное мышление. Он уже может рассуждать, опираясь на логику.
Произвольность познавательных процессов у учащихся 5-х классов возникает лишь на пике волевого усилия, когда ребенок специально организует себя под напором обстоятельств или по собственному побуждению. В процессе взросления меняется возможность управления вниманием, памятью. Учащийся в состоянии управлять ими по своей воли.
Познавательная активность ребенка, направленная на обследование окружающего мира организует его внимание на исследуемых объектах довольно долго, пока не иссякнет интерес. Детям трудно сосредоточиться на однообразной и малопривлекательной для них деятельности или на деятельности интересной, но требующей умственного напряжения. Чтобы удерживать свое внимание на интеллектуальных задачах, дети должны приложить усилия.
Подросток может управлять своим вниманием, концентрировать его в значимой для себя деятельности. На уроке внимание подростка нуждается в поддержке со стороны учителя.
Ребенок может сознательно пользоваться приемами запоминания. Он повторяет то, что надо запомнить, старается смыслить, осознать запоминаемое в заданной последовательности. Однако непроизвольное запоминание остается более продуктивным. В процессе учебной деятельности запоминание должно быть произвольным. Это становится возможным, если ребенок понимает то, что он должен запомнить. В процессе обучения ребенок приходит к пониманию необходимости заставит работать на себя свою память. В подростковый период учащийся способен управлять своим произвольным вниманием. Память перестраивается, переходя от доминирования механического запоминания к смысловому. При этом перестраивается сама смысловая память - она приобретает логический характер, обязательно включается мышление. Становится более доступным запоминание абстрактного материала. Важным стимулом к учению является притязания на признание среди сверстников. Знания приобретают для учащихся особую значимость.
1.6. Педагогические основы в обучении решения задач
В обучении математике роль задач определяется, с одной стороны, тем, что конечные цели этого обучения сводятся к овладению учащихся методами решения определенной системы математических задач. С другой стороны, она определяется и тем, что полноценное достижение целей обучения возможно лишь с помощью решения учащимися системы учебных и математических задач. Таким образом, решение задач в обучении математике выступает и как цель, и как средство обучения. Важнейшей функцией решения задач является функция формирования и развития у учащихся общих умений решений любых математических (в том числе и прикладных) задач. Общее умение по решению задач следует отличать от частных умений решения задач определенного вида. В основе частных умений лежит изучаемые учащимися частные методы (алгоритмы и эвристические схемы) решения задач данного вида. Считается, что общие умения могут возникнуть лишь благодаря решению большого числа задач. «Если хотите научиться решать задачи, то решайте их!» - советует Д. Пойа. Следуя этому совету, учителя предлагают учащимся огромное количество задач и затрачивают на их решение не менее половины всего учебного времени. А результаты этой работы более чем скромные: большинство учащихся, встретившись с задачей незнакомого или малознакомого вида, не знают, как к ней подступиться, с чего начать решение, и при этом обычно произносят: «А мы такие не решали».
Общие знания о задачах и механизмах их решения нужны для того, чтобы решение задач приносило наибольший познавательный эффект, чтобы процесс их решения превратился в подлинный метод обучения учащихся определенным знаниям и навыкам.
Каковы же знания, которые должны быть усвоены учащимися о задачах и их решении?
Это общие представления о задачах и процессах их возникновения из реальных и абстрактных проблемных ситуаций; о составных частях и структуре задач; об основных видах задач в зависимости от характера объекта и требований задачи; общие представления о сущности процесса решения задач и конкретизация их в отношении каждого вида задач; о структуре и этапах процесса решения задач.
Главное - сформировать такой общий подход к решению задач, когда задача рассматривается как объект для анализа, для исследования, а ее решение - как конструирование и изобретение способа решения. Это осуществляется в процессе обучения математике с помощью основополагающих принципов дидактики. Действительно, в обучении реализуются следующие принципы:
1. Принцип научности отражает взаимосвязь с современным научным знанием. Этот принцип воплощается в отборе изучаемого материала, в порядке и последовательности введения научных понятий в учебный процесс.
Принцип научности нацеливает учителя на вовлечение школьников в проведение анализа результатов собственных наблюдений, в самостоятельное их (результатов) исследование.
2. Принцип систематичности и последовательности придает системный характер учебной деятельности, теоретическим знаниям, практическим умениям учащегося. Этот принцип предполагает усвоение знаний в определенном порядке, системе. Требование систематичности и последовательности в обучении нацелено на сохранение преемственности содержательной и процессуальной сторон обучения, при которых каждый урок -это логическое продолжение предыдущего как по содержанию изучаемого учебного материала, так и по характеру, способам выполняемой учениками учебно-познавательной деятельности.
При решении задачи с помощью уравнения может усложняться характер взаимосвязи между элементами условия задачи, уравнения по мере того, как изучается новый материал и ученик приобретает новые знания, умения.
3. Принцип связи обучения с практикой предусматривает, чтобы процесс обучения стимулировал учеников использовать полученные знания в решении практических задач, анализировать и преобразовывать окружающую действительность. Для этого используется анализ примеров и ситуаций из реальной жизни, соотнесение с жизненными ситуациями условия задачи, анализ условия задачи.
4. Принцип доступности требует учета особенностей развития учащихся, анализа материала с точки зрения их реальных возможностей и такой организации обучения, чтобы они не испытывали интеллектуальных, моральных, физических перегрузок.
Доступность должна заключаться в обучении учащихся новому материалу, опираясь на их знания, опыт, особенности мышления. Например, при решении задач с помощью составления уравнений учащиеся должны уметь решать прежде всего сами уравнения.
-
Принцип наглядности означает, что эффективность обучения зависит от целесообразного привлечения органов чувств к восприятию и переработке учебного материала. В процессе обучения используются наглядные средства: модели, рисунки, схемы и т.п.
Виды, наглядности, которые могут быть использованы при решении задач, это:
-
экспериментальная наглядность (опыты, эксперименты);
-
символическая и графическая наглядность (графики, схемы и т.п.);
-
внутренняя наглядность (образы, создаваемые речью учителя).
Однако использование наглядности должно быть в той мере, в какой она способствует формированию знаний и умений, развитию мышления. Так, при решении задачи, ученик должен переходить от образного представления процессов, описываемых в ней, к их записи с помощью схем, графиков и оперировать уже со знаками и символами.
ГЛАВА ІІ
МЕТОДИКА ОБУЧЕНИЯ УЧАЩИХСЯ РЕШЕНИЮ
ТЕКСТОВЫХ ЗАДАЧ АРИФМЕТИЧЕСКИМ СПОСОБОМ.
2.1. Знания, умения, навыки учащихся по решению текстовых задач по окончании начальной школы.
Начальный курс математики раскрывается на системе целесообразно подобранных задач. Значительное место занимают в этой системе текстовые задачи. При рассмотрении смысла арифметических действий, связи существующей между действиями, и взаимосвязи между компонентами и результатами действий непременно используются соответствующие простые текстовые задачи (задачи, решаемые одним арифметическим действием). Текстовые задачи служат также одним из важнейших средств ознакомления детей с математическими отношениями, выражаемыми словами «быть на столько-то больше (меньше)», «быть на столько-то раз больше (меньше)». Они используются и в целях уяснения понятия доли (задачи на нахождение доли величины и искомого значения величины по доле). Текстовые задачи помогают и при формировании ряда геометрических понятий, а также при рассмотрении элементов алгебры.
Если мы хотим сформировать у школьников правильное понятие о сложении, необходимо, чтобы дети решили достаточное количество простых задач на нахождение суммы, практически выполняя каждый раз операцию объединения множеств без общих элементов. Выступая в роли конкретного материала для формирования знаний, задачи дают возможность связать теорию с практикой, обучение с жизнью. Решение задач формирует у детей практические умения, необходимые каждому человеку в повседневной жизни. Например, подсчитать стоимость покупки, вычислить в какое время надо выйти, чтобы не опоздать на поезд и т.п.
Использование задач в качестве конкретной основы для ознакомления с новыми знаниями и для применения уже имеющихся у детей знаний играет исключительно важную роль в формировании у детей элементов материалистического мировоззрения. Решая задачи, ученик убеждается, что многие математические понятия, имеют корни в реальной жизни, в практике людей.
Через решение задач дети знакомятся с важными в познавательном и воспитательном отношении фактами. Так, содержание многих задач, решаемых в начальных классах, отражает труд детей и взрослых, достижения нашей страны в области народного хозяйства, техники, науки, культуры.
Сам процесс решения задач при определенной методике оказывает весьма положительное влияние на умственное развитие школьников, поскольку он требует выполнения умственных операций: анализа и синтеза, конкретизации и абстрагирования, сравнения, обобщения. Так, при решении любой задачи ученик выполняет анализ: отделяет вопрос от условия, выделяет данные и искомые числа; намечая план решения, он выполняет синтез, пользуясь при этом конкретизацией (мысленно рисует условие задачи), а затем абстрагированием (отвлекаясь от конкретной ситуации, выбирает арифметические действия); в результате многократного решения задач какого-либо вида ученик обобщает знания связей между данными и искомым в задачах этого вида, в результате чего обобщается способ решения задач этого вида.
Задачи выполняют очень важную функцию в начальном курсе математики - они являются средством развития у детей логического мышления, умения проводить анализ и синтез, обобщать, абстрагировать и конкретизировать, раскрывать связи, существующие между рассматриваемыми явлениями. Кроме того, решение задач способствует воспитанию терпения, настойчивости, воли, способствует пробуждению интереса к самому процессу поиска решения, дает возможность испытать глубокое удовлетворение, связанное с удачным решением.
Овладение основами математики немыслимо без решения и разбора задачи, что является одним из важных звеньев в цепи познания математики, этот вид занятий не только активизирует изучение математики, но и прокладывает пути к глубокому пониманию её. Работа по осознанию хода решения той или иной математической задачи даёт импульс к развитию мышления ребенка. Решение задач нельзя считать самоцелью, в них следует видеть средство к углублённому изучению теоретических положений и вместе с тем средство развития мышления, путь осознания окружающей действительности, тропинку к пониманию мира.
К началу 5-го класса учащиеся должны знать связи между такими величинами, как цена, количество, стоимость; время, скорость, путь при равномерном движении; уметь применять к решению текстовых задач знание изученных зависимостей. Таковы основные требования к знаниям, умениям и навыкам обучающихся, обеспечивающие преемственную связь с курсом математики 5 класса, предъявляемые программой.
Основная цель обучения решению текстовых задач в начальной школе - осознанное усвоение детьми смысла арифметических действий, отношений «больше» - «меньше» (на несколько единиц и в несколько раз), «столько же» (или «равно»), взаимосвязи между компонентами и результатами действий, использованию действий вычитания (деления) для сравнения чисел.
Поэтому можно выделить следующие ключевые задачи, которые должны уметь решать выпускники начальной школы:
-
нахождение суммы величин, если эти величины известны с использованием сравнений «на…больше», «на…меньше», «в..раз больше», «в… раз меньше» в прямой и косвенной форме;
-
нахождение разницы между величинами с использованием действий вычитания и деления;
-
нахождение одной из трёх величин в задачах на зависимости:
цена-количество-стоимость, норма расхода материала на 1 вещь-количество вещей-расход материала всего, скорость-время-расстояние;
-
нахождение одной из трёх величин в задачах на зависимости:
было-израсходовали-осталось, было-добавили-стало.
2.2. Планирование работы учителя по обучению решению текстовых задач арифметическим способом.
Несмотря на требования к знаниям, умениям учащихся, предъявляемые программой начальной школы, большинство учащихся начальной школы приходят в 5-й класс с небольшим багажом знаний и умений именно по решению текстовых задач. Поэтому основная цель моей работы на первых уроках математики в 5 классе во время повторения учебного материала - определить пробелы в знаниях и умениях учащихся, в том числе и по решению текстовых задач. Простейшие задачи в одно действие можно включить в тренировочные упражнения для устного счёта (см. приложение 1). При решении таких задач следует обращать внимание учащихся на те числовые данные, которые выражены не только числами, но и словами.
Иногда при анализе задач обнаруживается неумение некоторыми учащимися переводить на математический язык слова для сравнения величин. В таких случаях можно использовать таблицу, которую надо составить вместе с учениками на первых уроках математики.
-
больше
меньше
выше
толще
шире
дороже
старше
длиннее
глубже
дальше
ниже
тоньше
уже
дешевле
младше
короче
мельче
ближе
Как было сказано выше, существуют различные подходы к определению типов задач. Несмотря на то, что любая классификация условна, обойтись без неё невозможно. При планировании учебного материала и подготовке к урокам можно выделить ключевые задачи, приёмы решения которых должны освоить учащиеся 5 и 6 классов.
-
Задачи на процессы (на движение, на работу, на бассейны)
-
Задачи на нахождение двух или нескольких чисел по их сумме и разности; задачи на нахождение двух или нескольких чисел по их сумме (разности) и отношению.
-
Задачи на предположение.
-
Задачи на проценты.
-
Задачи на нахождение части от числа и числа по его части.
-
Задачи на пропорциональные зависимости.
Все эти задачи содержат новые приёмы решения. Поэтому требуется серьёзная подготовка к обучению.
В учебниках «Математика 5» и «Математика 6» автора Н.Я. Виленкина, по которым я работаю, задачи разных видов «разбросаны», не систематизированы ни по сложности, ни по приёмам решения. Очевидно, для того, чтобы разрушить формирующиеся стереотипы решения, разнообразить способы деятельности учащихся. Но, на мой взгляд, при освоении нового приёма решения такого разнообразия лучше избегать и следовать «от простого к сложному». И только после того, как приём освоен и сформирован навык по его применению, его можно использовать и при решении составных задач разных видов.
Наиболее целенаправленно арифметический подход к решению текстовых задач раскрывается в учебниках «Арифметика 5», «Арифметика 6» С.М. Никольского и «Математика 5», «Математика 6» Г.В. Дорофеева.
2.3. Организация работы учителя на каждом этапе решения задачи.
Как было сказано выше, работа над задачей включает 4 основных этапа. Причём все четыре этапа одинаково важны. Поэтому рассмотрим работу учителя и учащихся на каждом отдельном этапе при решении задач разных видов.
-
Организация работы учителя над условием задачи.
На первом этапе необходимо добиться того, чтобы учащиеся «приняли задачу», то есть поняли её смысл, сделав целью своей деятельности. С этой целью оформляется краткая запись. Для разных видов задач это можно сделать по-разному.
Примеры:
1. С одной и той же станции в одно и то же время вышли в противоположных направлениях два поезда. Скорость одного поезда 50 км/ч, а другого 85 км/ч. Какое расстояние будет между поездами через 3 часа?
Краткую запись к данной задаче (и любой задаче на движение) удобно выполнить в виде схематического чертежа.
Графическая иллюстрация создаёт перед учениками пространственный образ, помогает в задачах на движение правильно расположить те неподвижные точки, с которыми условие связывает движущийся объект.
Далее можно составить таблицу, которая поможет в определении известных и неизвестных величин и отношений между ними.
v
t
s
1-й поезд
50 км/ч
3 ч
?
2-й поезд
85 км/ч
3 ч
?
В задачах на нахождение двух или нескольких величин по их отношению и сумме (или разности), а также в задачах на части удобно краткую запись оформить в виде отрезков. Учащиеся должны научиться принимать подходящую величину за 1 часть, определять, сколько таких частей приходится на другую величину, на их сумму (разность).
Например:
2. За рубашку и галстук заплатили 40 р. Рубашка дороже галстука в 4 раза. Сколько стоит галстук?
3. В первой пачке было на 10 тетрадей больше, чем во второй, а всего 70 тетрадей. Сколько тетрадей было во второй пачке?
К этой задаче краткую запись можно выполнить в виде столбчатой диаграммы.



4. Для санатория купили 12 кресел и 50 стульев на общую сумму 9880 руб. Сколько стоит одно кресло, если один стул стоит 86 руб.
Оформить краткую запись можно с помощью таблицы:
Цена
Количество
Стоимость
Кресла
?
12
?
Стулья
86 руб
50
?
5. В двух комнатах было 56 человек. Когда в первую пришли ещё 12 человек, а во вторую - 8 человек, то людей в комнатах стало поровну. Сколько человек было в каждой комнате первоначально?
было
стало




Правильно составленная краткая запись указывает на сознательный анализ учеником условия и требования задачи и намечает план дальнейшего решения.
2.3.2. Организация работы учителя по составлению плана решения.
Чаще всего при организации поиска решения задачи применяется аналитико - синтетический метод.
Рассмотрим план рассуждений на примере задачи 1.
1. С одной и той же станции в одно и то же время вышли в противоположных направлениях два поезда. Скорость одного поезда 50 км/ч, а другого 85 км/ч. Какое расстояние будет между поездами через 3 часа?
В задаче требуется узнать расстояние между поездами через 3 часа.
- Что для этого надо знать?
- s , которое прошёл 1-й поезд за 3 часа, и s , которое прошёл 2-й поезд за 3 часа.
- Что необходимо знать для определения этих расстояний?
- скорость каждого поезда, а это в задаче известно.
План решения следующий:
1) находим s, которое прошёл 1-й поезд за 3 часа
2) находим s, которое прошёл 2-й поезд за 3 часа
3) находим общее расстояние.
Рассмотренный метод составления плана решения задачи является аналитическим. Иногда поиск решения осуществляется синтетическим путём. Например, задача:
2. Молодой рабочий выполнил задание за 8 часов, изготовляя в час по 18 деталей. За сколько часов выполнит то же задание его наставник, если в час он делает на 6 деталей больше, чем молодой рабочий?
Краткая запись
Количество
деталей в час
Время работы
Всего деталей
Рабочий
18 дет.
8 ч
одинаковое
Наставник
на 6 дет. больше
?
одинаковое
План рассуждений:
- зная скорость работы и время работы молодого рабочего, можно определить его объём работы - количество изготовленных деталей;
- поскольку задание одинаковое, то мы определим и объём работы наставника;
- зная скорость работы рабочего и разницу в скоростях работы наставника и рабочего, можно определить скорость работы наставника;
- зная скорость работы наставника и количество изготовленных им деталей, можно определить время его работы.
3. С бахчи собрали 27 т арбузов. В столовую направили 2/9 этих арбузов, а 6/7 остатка отвезли на рынок. Сколько тонн арбузов отвезли на рынок?
Краткая запись:
Собрали всего 27 т
столовая 2/9 от 27 т
рынок 6/7 от остатка ?
Применяем аналитический метод рассуждений: чтобы узнать…надо знать… Начинаем, как обычно, с вопроса к задаче.
- чтобы узнать сколько тонн арбузов отвезли на рынок, надо знать остаток;
- чтобы найти остаток, надо знать сколько «было» и сколько «взяли»;
- «было» известно, «взяли», то есть увезли в столовую, можно найти.
После такого устного аналитического разбора задачи выстраивается план решения уже синтетическим путём.
1. Находим количество арбузов, отвезённых в столовую.
2. Находим количество арбузов, оставшихся после этого.
3. Находим количество арбузов, отвезённых на рынок.
-
Реализация плана решения.
Различные формы объяснения решения задачи - это различные ступени логического мышления учеников. Как было сказано выше, объяснение решения задачи имеет различные формы. В своей практике при работе в классе я применяю чаще всего такую форму объяснения: краткий вопрос и следующее за ним действие. При выполнении домашних задач я требую от учащихся подробных объяснений к каждому действию.
Рассмотрим ход решения на примере одной из задач на нахождение числа по его части.
1. Когда Костя прошёл 0,3 всего пути от дома до школы, ему ещё осталось пройти до середины 150 м. Какой длины путь от дома Кости до школы?
При подробном анализе данной задачи и оформления краткой записи (см. ниже) ход рассуждений может быть следующим:
Если Костя прошёл 3/10 всего пути, значит весь путь разделён на 10 частей. Следовательно, для нахождения всего пути надо найти 1/10 часть его. На схеме хорошо видно, что до середины оставалось 2/10 пути, а это 150 км. ( Половина- это 0,5; 0,5-0,3). Значит, можно найти 1\10 часть (150:2). Зная 1/10 часть, находим 10 частей (умножаем полученное на 10).
Ход решения.
Сначала найдем часть пути, оставшуюся до середины.
-
0,5-0,3=0,2(пути) осталось пройти до середины.
Теперь можно найти 1/10 часть.
-
150:2=75(м) составляет 1/10 часть всего пути.
Находим весь путь.
-
75 . 10=750(м) весь путь.
2.3.4. Анализ найденного решения и работа по поиску других
вариантов решения.
Проверка решения задачи является моментом очень ценным для развития сознательности и самоконтроля. Часто учащиеся записывают ответ не задумываясь.
Как проверить решение?
Во-первых, сравнить с реальностью. Например, при решении задачи на нахождение скорости пешехода ученик получил ответ 25км/ч. При анализе найденного решения, приходим к выводу что такая скорость для пешехода нереальна. Или, находя часть класса, состоящего из 25 человек (к примеру 30%), учащаяся получила 750 человек.. Анализируя, понимаем, что часть от числа не может быть больше самого числа.(30% меньше 100%).
Во-вторых, если результат реален, то надо проверить задачу на выполнение всех требований. Например, в задаче 1. (см выше) это можно сделать следующим образом.
Какой путь прошёл Костя? 750:10 3=225 м.
Если он пройдёт ещё 150 м, это будет середина пути? 225+150=375 м, 750:2=375 м.
Полезно предлагать учащимся применять различные варианты решения одной задачи, что приводит к выбору наиболее рационального способа решения и в то же время является проверкой результата.
Примеры:
1. Два пешехода одновременно вышли в противоположных направлениях из одного пункта. Скорость первого 4 км/ч, скорость второго 5 км/ч. Какое расстояние будет между ними через 3 часа?
1 способ.
1. 4 . 3=12 (км) прошёл 1-й пешеход за 3 ч
2. 5 . 3=15 (км) прошёл 2-й пешеход за 3 ч
3. 12+15=27 (км) расстояние между пешеходами через 3 ч
2 способ.
1. 4+5=9 (км/ч) удаляются пешеходы друг от друга каждый час (общая скорость)
2. 9 3 =27 (км) расстояние между пешеходами через 3 ч
2.В первой коробке на 6 карандашей больше, чем во второй, а в двух вместе - 30 карандашей. Сколько карандашей в каждой коробке?
1 способ.
Если уменьшить количество карандашей в первой коробке на 6, то и сумма уменьшится на 6. Количество карандашей в коробках при этом будет одинаковым. То есть, 30-6=24; 24:2=12(к)-в меньшей коробке и 12=6 =18(к)- в большей коробке.
2 способ.
Если увеличить количество карандашей во второй коробке на 6, то и сумма увеличится на 6. Количество карандашей в коробках при этом будет одинаковым. То есть, 30+6=36(к); 36:2=18(к)-в большей коробке, 18-6=12(к(- в меньшей коробке.
3 способ.
Можно уравнять количество карандашей в коробках, если половину излишка переложить в меньшую коробку. При этом сумма не изменится. То есть 6:2=3 (к)-добавляется в меньшую коробку и убавляется из большей коробки; 30:2=15; 15+3=18(к)-в большей коробке, 15-3=12(к) - в меньшей коробке.
2.4. Формирование приёмов решения задач «на процессы».
Умение решать задачи данного класса очень важно.
Во-первых, в учебниках математики большое количество задач связано с разного рода процессами, начиная с 5 класса и по 9 класс. Во-вторых, отношения между величинами, «участвующими» в задачах данного типа, встречаются при изучении других смежных дисциплин, таких как физика и химия. Хорошо усвоенные арифметические приёмы решения данных задач позволяют без особого труда перейти и к алгебраическому способу их решения. Основная причина затруднений, которые обычно испытывают учащиеся при решении задач «на процессы», заключена не в исполнительной части деятельности, а в правильном выборе действий. Успешное решение задач данного класса предполагает знание зависимостей между тремя величинами: скоростью протекания процесса (v), временем (t) и его результатом (условно можно обозначить (s).
Важно, чтобы у учащихся сформировались правильные понятия о каждой из этих величин и их зависимостях.
2.4.1. Формирование понятия о времени протекания процесса.
Некоторые учащиеся даже в 5-м классе плохо ориентируются во временных интервалах. При формировании этого понятия в некоторых случаях необходимо отработать временные интервалы с переходом через 12 часов дня и 12 часов ночи. С этой целью предлагаются задачи, например такого содержания:
1. Поезд отправился от пункта А в 9 часов утра и прибыл в пункт В в три часа дня. Сколько времени был в пути поезд?
2. Туристы вышли в поход в семь часов утра, а вернулись в 18 часов того же дня. Сколько времени туристы были в походе?
3. Сколько времени пройдёт от семи вечера до трёх часов ночи?
4. В 10 часов утра открылся кран. Сколько времени из него текла вода, если отремонтировали его в час дня?
2.4.2. Формирование понятий о скорости протекания процесса и его продукте (результате).
При формировании понятия скорости важно добиться от учащихся понимания того, что данное понятие относится не только к движению. Скорость - это часть продукта (результата) и выражается «чем-то», выполненным в единицу времени. Простейшие задачи на определение скорости процесса:
1. Машинистка напечатала 120 страниц за 4 часа. Сколько страниц машинистка печатала за 1 час?
2. Бак ёмкостью 60 литров наполнился за 6 минут. Сколько литров в минуту наливалось в бак?
3. За двадцать лет дуб вырос на 60 дм. Определите на сколько дециметров дуб вырастал в среднем каждый год?
В дальнейшем вопросы к задачам такого типа можно ставить в такой форме: определить скорость работы машинистки, скорость наполнения бака, скорость роста дерева.
Чтобы проверить насколько учащиеся осознанно оперируют величинами, я использую задачи, которые могут провоцировать неверные действия, то есть такие, в которых нахождение либо v, либо t приводит к нецелому числу.
Например:
1. За 5 минут кран наливает 1 ведро воды. Сколько вёдер нальёт кран за минуту?
2. За 21 день строители возвели 3 здания. Сколько зданий они строили за день?
3. Машина прошла 2 км со скоростью 50 км/ч. Сколько времени ехала машина?
Краткую запись к задачам «на процессы» можно оформить в виде таблицы: в первой строчке таблицы записываем условное обозначение величин, а во второй расшифровываем эти величины применительно к каждой задаче, в третьей строчке вписываем числовые данные.
При анализе условия задачи полезно учащимся задавать вопросы:
-
Кто «участвует» в задаче?
-
Что он (они) делают? Сколько (s) ?
-
Сколько времени делают (t ) ?
-
Сколько выполняет за 1 единицу времени (v) ?
Такие вопросы можно повесить у доски или оформить на карточках каждому учащемуся.
Отвечая на вопросы, учащиеся заполняют таблицу.
Например, к задаче 2 (см. выше) краткая запись выглядит так:
v
t
s
Количество зданий
за 1 день
Время работы
Всего
зданий
?
21 день
3 здания
При решении большого количества таких простых задач у учащихся формируется навык их решения. Они понимают, как надо находить v, t, или s по известным двум другим величинам.
Полезны задачи с лишними или недостающими данными, которые показывают наличие двух величин для определения третьей.
Примеры:
1. Пешеход отправился в путь в 5 часов утра. С какой скоростью он пройдёт 10 км?
2. За какое время бригада, состоящая из 5 человек, сделает 100 деталей, если она работает со скоростью 25 деталей в час?
3. Ученики 5 класса сажали деревья. Они начали работу в 10 часов утра, в час сажали по 3 дерева. Сколько деревьев они посадят через 3 часа?
4. Три землекопа копали канаву длиной 21 м. За какое время они её выроют?
2.4.3. Формирование понятия совместного действия.
Второй уровень сложности задач «на процессы» связан с ситуацией совместного действия». Решение этих задач осложнено следующими факторами:
1. Числом «участников»: действуют не один объект, а несколько.
2. Характером взаимодействия: помогают или противодействуют.
3. Временем включения в процесс: одновременно или в разное время включились в совместное действие.
4. Дополнительными отношениями основных величин: появляются отношения между общими и частными значениями каждой величины. Так общая скорость (v0)теперь является не только функцией общего времени (t0) и общего суммарного продукта (s0), но и функцией частных значений скоростей.
Действуя по схеме «от простого к сложному», вначале следует организовать работу по усвоению отношений между суммарным «продуктом» как результатом совместных действий всех участников и частными «продуктами»; между общей скоростью участников и частными скоростями; между общим временем процесса и временем действия отдельных участников. Особое внимание при этом следует уделить характеру взаимодействия: помогают или противодействуют.
Примеры задач на функциональную зависимость: v0=f ( v¡); s0= f (s¡).
1. Две бригады собирали фрукты. Одна собрала 800 кг, а другая 700 кг. Сколько кг фруктов они соберут вместе? s0= s1+ s2
2. Два пешехода вышли навстречу друг другу. Один прошёл до встречи 10 км, а другой 8 км. Какое общее расстояние они прошли до встречи? s0= s1+ s2
3. Из одного пункта в противоположных направлениях вылетели два самолёта. Один летел со скоростью 800 км/ч, а другой со скоростью 700 км/ч. С какой скоростью они удаляются друг от друга? v 0= v 1+ v 2
4. Одна труба наливает 10 литров за 1 минуту, а вторая 15 литров за 1 минуту. Сколько литров за 1 минуту нальют обе трубы? v 0= v 1+ v 2
5. Из одного пункта в одно и то же время в одну сторону выехали два велосипедиста. Один проехал 30 км а второй 25 км. На какое расстояние они удалились? s0= s1- s2
6. Кран наливает бочку: каждую минуту 10 литров. А из отверстия в бочке выливается вода со скоростью 2 л в минуту. Какой объём воды набирается в бочке каждую минуту? v 0= v 1- v 2
Анализ задач на процессы с несколькими участниками можно проводить по следующим вопросам:
-
Сколько участников процесса?
-
В одно время включаются в процесс или в разное?
-
Как они взаимодействуют:помогают или противодействуют?
-
Что известно в задачах об общих величинах v, t, s?
-
Что известно в задачах о частных величинах v, t, s?
-
Что требуется узнать?
Краткая запись оформляется в виде таблицы, количество строк которой увеличивается на количество участников процесса.
Рассмотрим работу с классом по решению задачи на каждом этапе.
Например задача:
Две тракторные бригады вспахали вместе 762 га поля. Первая бригада работала 8 дней и каждый день вспахивала 48 га. Сколько гектаров поля вспахивала каждый день вторая бригада, если она работала 9 дней?
1 этап. Анализируем условие задачи, отвечая на вопросы.
-
2 участника, 2 тракторные бригады.
-
Не известно.
3) Помогают, значит s0= s1+ s2
Ответы на остальные пункты можно сразу внести в таблицу.
v
t
s
Площадь, вспаханная
за 1 день
Время работы
Площадь
всего
1 бригада
48 га
8 дней
?
2 бригада
?
9 дней
?
2 этап. План рассуждений.
Используем аналитический метод рассуждений. Начинаем с вопроса к задаче.
-Чтобы узнать скорость работы 2-й бригады (v2), надо знать площадь, вспаханную ей (s2) и время её работы (t2).
-Время работы известно, а площадь нет.
-Чтобы узнать площадь s2, надо знать общую площадь s0 и площадь, вспаханную первой бригадой s1. s0 известно, а s1 нет.
-Чтобы найти s1, надо знать v1 и t 1. Это в задаче известно.
3 этап. План решения.
Найти s1, затем s2, затем v2.
-
48 * 8=364(га) вспахала 1-я бригада за 8 дней.
-
762-364=398(га) вспахала 2-я бригада всего.
-
398:9=47(га) вспахивала 2-я бригада за 1 день.
4 этап. Проверка полученного результата.
Сначала убедимся в достоверности результата. После этого проверим, сколько га вспахала каждая бригада за всё время работы. Получится ли всё поле. Можно предложить детям поискать другой вариант решения.
2.5. Составление задач учащимися.
При работе с арифметической задачей нельзя пройти мимо вопроса о самостоятельном составлении задач учениками. При решении задач того или другого вида проверить качество усвоения вопроса можно такими заданиями: придумать задачу, в которой надо найти одну из трёх величин скорость протекания процесса, время или продукт его сначала с одним объектом, а потом с несколькими. Придумать задачу, в которой требуется найти часть от числа, составить задачу на прямую пропорциональную зависимость и т.д. При этом вначале, следуя принципу «от простого к сложному», предлагаются задачи в одно действие.
Необходимо избегать шаблона в этой работе, когда составляется слишком большое количество задач совершенно однотипных. Такая работа для учеников мало продуктивна. Вслед за простенькими задачами можно предложить ученикам составлять так называемые комбинированные задачи, то есть такие, в которых к новому материалу предлагается присоединить материал, пройденный ранее. При этом, конечно, следует учитывать способности разных учащихся. Если ученику не под силу составление сложной задачи, пусть он придумает простую или предложить составить задачу по готовому условию, которое оформлено, например, в виде таблицы:
V
t
90 км S
S
Объект 1
15км/ч
2ч
Объект 2
5ч
Для составления задач надо учащимся дать ряд указаний:
1. Задача должна иметь все необходимые данные и чётко поставленный вопрос.
2. Предметное содержание и числовые соотношения задачи должны соответствовать действительности.
3. Очень желательно, чтобы числовые данные, хотя бы частично, добывались самими учащимися, для этого рекомендовать использовать журналы, газеты, исторический материал, производственную практику родителей.
Составление условия задачи - хорошее упражнение в краткой и точной математической речи.
При таком подходе к составлению задач ясно, что работа эта вызывает большую самостоятельность, интерес, развивает творчество.
Примеры решения задач арифметическим способом.
Решение задач на сравнение и переливание
Задача 1
Из восьмилитрового ведра, наполненного молоком, надо отлить 4 литра с помощью двух пустых бидонов: трехлитрового и пятилитрового.
Решение.
-
Переливаем из восьмилитрового ведра 5 литров молока в пятилитровое.
2. Переливаем из пятилитрового ведра 3 литра в трёхлитровое.
3. Переливаем их теперь в восьмилитровое ведро. Итак, теперь трёхлитровое ведро пусто, в восьмилитровом 6 литров молока, а в пятилитровом - 2 литра молока.
4. Переливаем 2 литра молока из пятилитрового ведра в трёхлитровое, а потом наливаем 5 литров из восьмилитрового в пятилитровое. Теперь в восьмилитровом 1 литр молока, в пятилитровом - 5, а в трёхлитровом - 2 литра молока.
5.Доливаем дополна трёхлитровое ведро из пятилитрового и переливаем эти 3 литра в восьмилитровое ведро. В восьмилитровом ведре стало 4 литра, так же, как и в пятилитровом. Задача решена.
2 способ.
Нальем до половины оба бидона (половина определяется при помощи наклона бидонов). Получим 2,5 и 1,5 литров молока в пятилитровом и трехлитровом бидонах соответственно. Выльем все молоко из техлитрового в пятилитровый бидон. Получим в нем 4 литра молока.
Задача 2. Есть 27 монет. Известно, что одна из них фальшивая (по весу тяжелее настоящих). Как за три взвешивания на чашечных весах без гирь определить фальшивую монету?
Решение.
Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую; кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части.
Задача 3. В корзине лежат 13 яблок. Имеются весы, с помощью которых можно узнать суммарный вес любых двух яблок. Придумайте способ выяснить за 8 взвешиваний суммарный вес всех яблок.
Решение.
Занумеруем яблоки. Взвесим первое яблоко со вторым, второе с третьим и третье с первым, затем сложим полученные веса (где-нибудь в тетради) и получим удвоенный вес трех яблок, а затем и вес трех яблок, следовательно, за три взвешивания мы узнали суммарный вес первых трех яблок. Осталось пять взвешиваний и десять яблок, которые взвешиваем попарно и, суммируя все данные, получим вес 13 яблок.
Решение задач на числовые последовательности.
-
Вася задумал число, умножил его на 2, прибавил 3 и получил 17. Какое число он задумал?
Решение.
Будем действовать "с конца": чтобы узнать, какое число получил Вася перед тем, как получить 17, отнимем от 17 число 3, а затем разделим результат на 2, чтобы узнать исходное число.
(17-3):2=7.
-
Алеша задумал число. Он прибавил к нему 5, потом разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число задумал Алеша?
Решение аналогично решению задачи 1. ((2х7+6):4)х3-5=10
-
В стакане находится одна бактерия. Через секунду она делится пополам. Каждая из получившихся бактерий через секунду также делится пополам и так далее. Через минуту стакан заполнился. Через какое время стакан был заполнен наполовину?
Решение.
По условию задачи, каждую секунду количество бактерий в стакане удваивается. Значит, половина стакана заполнится ровно на секунду раньше, чем полный стакан, то есть за 59 секунд.
-
Один Бездельник захотел получить денег и заключил сделку с Чёртом. Теперь каждый раз, когда Бездельник переходит мост через речку, количество имеющихся у него денег удваивается. Но за это он отдаёт Чёрту каждый раз по 24 копейки. Сколько денег было у Бездельника, если он прошёл по мосту 3 раза и деньги у него закончились?
Решение.
После того, как Бездельник в третий раз прошёл по мосту, он заплатил 24 копейки Чёрту и остался без денег. Значит,после того, как он в третий раз прошёл по мосту у него было ровно 24 копейки, а до этого - 24:2=12 копеек. Эти деньги оказались у Бездельника после того, как он во второй раз прошёл по мосту и заплатил Чёрту. Значит, до этого у него было (12+24):2=36:2=18 копеек. А до первого прохода по мосту, то есть в самом начале, у него была (18+24):2=42:2=21 копейка.
Задачи на проценты и отношения
-
В классе учится меньше 50 школьников. За контрольную работу седьмая часть учеников получила пятёрки, третья - четвёрки, половина - тройки. Остальные работы были оценены как неудовлетворительные. Сколько было таких работ?
Подсказка
Обратите внимание: число школьников, получивших ту или иную оценку всегда целое.
Решение
Поскольку число школьников, получивших ту или иную оценку, всегда целое, то для решения задачи нам надо найти целое число, меньшее 50, одновременно делящееся на 7, 3, 2. Единственным возможным ответом является число 42. Это значит, что всего в классе 42 ученика; 6 из них получили пятёрки; 14 - четвёрки; 21 - тройки. Следовательно, двойку получил 1 ученик.
-
"А это вам видеть пока рано", сказала Баба-Яга своим 33 ученикам и скомандовала: "Закройте глаза!" Правый глаз закрыли все мальчики и треть девочек. Левый глаз закрыли все девочки и треть мальчиков. Сколько учеников всё-таки увидели то, что видеть пока рано?
Решение
То, что видеть пока рано, две трети девочек увидели правым глазом, а две трети мальчиков - левым. Всего, стало быть, один глаз не закрыли две трети всех учеников - 22 человека.
-
Цены снижены на 20. На сколько процентов больше можно купить товаров на ту же зарплату?
Решение
Понижение цен на 20% означает, что новая цена товара равна старой, умноженной на 0.8. Значит, на прежнюю зарплату можно купить товаров в ![]() раз больше. Другими словами, на 25% больше.
раз больше. Другими словами, на 25% больше.
-
В течение года цены на штрюдели два раза поднимали на 50%, а перед Новым Годом их стали продавать за полцены. Сколько стоит сейчас один штрюдель, если в начале года он стоил 80 рублей?
Решение
После первого повышения цен штрюдель стал стоить 80*1.5=120 рублей; после второго повышения цен - 120*1.5=180 рублей; наконец, после двукратного снижения цены он стал стоить 180/2=90 рублей.
-
В гимназии все ученики знают хотя бы один из древних языков - греческий или латынь, а некоторые - оба языка. 85% всех ребят знают греческий язык, и 75% - знают латынь. Какая часть учащихся знает оба языка?
Подсказка
Заметьте, каждый гимназист знает хотя бы один древний язык.
Решение
Поскольку 85% всех ребят знают греческий язык, то 15% его не знают, т.е. знают латынь. Это значит, что из 75% ребят, знающих латынь, 15% не знают греческого, а оставшиеся 75% − 15% = 60% говорят на обоих языках.
-
Известно, что доля блондинов среди голубоглазых больше, чем доля блондинов среди всех людей. Что больше - доля голубоглазых среди блондинов или доля голубоглазых среди всех людей?
Решение
Пусть L - количество всех людей, B - количество блондинов, G - количество голубоглазых, D - количество голубоглазых блондинов. Условие задачи означает выполнение неравенства ![]() . Умножим обе части этого неравенства на
. Умножим обе части этого неравенства на ![]() . Получим
. Получим ![]() . А это и значит, доля голубоглазых среди блондинов больше, чем доля голубоглазых среди всех людей.
. А это и значит, доля голубоглазых среди блондинов больше, чем доля голубоглазых среди всех людей.
-
Эта задача насчитывает много сотен лет, но до сих пор поражает воображение своей красотой и неожиданностью. Три брата получили в наследство от отца 17 верблюдов. Старшему отец завещал половину стада, среднему - треть, а младшему - девятую часть. Братья пытались поделить наследство и выяснили, что старшему брату придётся взять 8 верблюдов и кусок верблюда, среднему - 5 верблюдов и кусок верблюда, а младшему - верблюда и кусок верблюда. Естественно, разрезать верблюдов не хотелось никому, и братья решили попросить помощи у Мудреца, проезжавшего мимо них на верблюде. Мудрец спешился и присоединил своего верблюда к стаду братьев. От нового стада из 18-ти верблюдов Мудрец отделил половину - 9 верблюдов для старшего брата, затем треть - 6 верблюдов для среднего брата, и, наконец, девятую часть - 2-х верблюдов для младшего брата. После успешной делёжки Мудрец сел на своего верблюда и продолжил путь. А братья стали думать, почему же каждый из них получил больше верблюдов, чем полагалось. Сможете ли вы объяснить, что же произошло?
Подсказка
Заметьте, 1/2 + 1/3 + 1/9 < 1.
Решение
Всё дело в том, что наследники с самого начала не заметили: завещанные им доли в сумме составляют вовсе не 100% наследства (как это бывает обычно), а всего 17/18 от общего количества. Так что даже если бы они решились, во имя буквального исполнения доли завещателя, резать верблюдов на части, то и тогда у них осталась бы лишней 1/18 доля наследства, т.е. лишних 17/18 верблюда.
Задачи на движение
-
Расстояние от моего дома до университета, где я работаю, 3 километра. Я прохожу это расстояние за полчаса, а профессор Чижиков за час. Однажды мы договорились встретиться. В 10 часов утра я вышел из дома, а Чижиков в это же время из университета. На каком расстоянии от университета это произойдет?
-
У Буратино и Пьеро был велосипед, на котором они отправились в соседнюю деревню. Ехали по очереди, но всякий раз, когда один ехал, другой шёл пешком, а не бежал. При этом они ухитрились прибыть в деревню почти в 2 раза быстрее, чем если бы оба шли пешком. Как им это удалось?
Подсказка
Попробуйте организовать путешествие так, чтобы и Буратино и Пьеро ровно полдороги проехал на велосипеде.
Решение
Буратино проехал на велосипеде полдороги, слез с него и дальше пошёл пешком. А Пьеро первую половину пути прошёл пешком, затем дошёл до велосипеда, сел на него и поехал. Таким образом они и сэкономили время.
-
Двое лыжников шли с постоянной скоростью 6 км/ч на расстоянии 200 метров друг от друга. Потом они стали подниматься в большую горку, и скорость упала до 4 км/ч. Потом оба лыжника съехали с горки со скоростью 7 км/ч и попали в глубокий снег, где их скорость стала всего 3 км/ч. Каким стало расстояние между ними?
Решение
Посмотрим, что происходило с расстоянием между лыжниками, когда они начали подниматься в горку. Сначала первый лыжник подошел к ее основанию; второй при этом отставал от первого на 200 метров. Когда подниматься в горку начал второй лыжник (это произошло через 0.2/6 часов), первый был от него на расстоянии (0.2/6) . 4 . 1000=200 . (4/6) метров, то есть начальное расстояние умножилось на отношение скоростей.
Рассуждая аналогично, получим, что в конце расстояние между лыжниками будет равно 200. (4/6) . (7/4) . (3/7)=200. (3/6)=100 метров.
-
По двум телевизионным каналам одновременно начали показывать один и тот же фильм. На первом канале фильм разбили на части по 20 минут каждая и вставили между ними двухминутные рекламные паузы. А на втором канале фильм разбили на части по 10 минут каждая и вставили между ними минутные рекламные паузы. На каком канале фильм закончится раньше?
Решение
На первом канале между началом каждой части и началом следующей проходит 22 минуты. За это время на втором канале пройдут две части по 10 минут и две минутные рекламные паузы. Следовательно, началу каждой части на первом канале соответствует тот же момент фильма на втором. Когда на первом канале начнётся последняя часть, до конца фильма останется 20 минут, рекламы уже не будет. На втором же канале покажут две части по 10 минут с минутной рекламной паузой, поэтому на первом канале фильм закончится на одну минуту раньше.
Задачи на сравнение(неравенства)
-
Обезьянки - Маша, Даша, Глаша и Наташа - съели на обед 16 мисочек манной каши. Каждой обезьянке что-то досталось. Глаша и Наташа вместе съели 9 порций. Маша съела больше Даши, больше Глаши и больше Наташи. Сколько мисочек каши досталось обезьянке Даше?
Подсказка
Заметьте, либо Глаша, либо Наташа получили не меньше 5 порций каши.
Решение
Глаша и Наташа вместе съели 9 мисочек, значит, одной из них досталось не меньше 5 мисочек. Но тогда Маша, которая съела больше каждой из них, должна была съесть не меньше 6 мисочек. Итого, эти 3 обезьянки съели не меньше 9 + 6 = 15 мисочек. Значит, Даше досталась только одна мисочка
-
В каждой комнате особняка стояли букеты цветов. Всего было 30 букетов роз, 20 - гвоздик и 10 - хризантем, причем, в каждой комнате стоял хотя бы один букет. При этом ровно в двух комнатах стояли одновременно и хризантемы, и гвоздики, ровно в трех комнатах - и хризантемы, и розы, ровно в четырех комнатах - и гвоздики, и розы. Могло ли в особняке быть 55 комнат?
Решение
Поставим в каждой комнате букеты одного сорта на отдельный столик (столиков будет не больше 60) и отметим по одному столику в каждой комнате. Оценим число неотмеченных столиков. Их 4 + 3 + 2 минус число комнат, где стоят цветы всех трех сортов (в такой комнате два неотмеченных столика, а при суммировании мы их сосчитали трижды). Но таких комнат не больше, чем комнат с хризантемами и гвоздиками, то есть не больше двух. Значит, неотмеченных столиков не меньше 7, а отмеченных (число которых равно числу комнат) - не больше 53.
Задачи на части и метод выравнивания.
-
На двух полках стоят книги. Всего 91 книга. При этом на нижней полке на 7 книг больше, чем на верхней. Сколько книг стоит на каждой полке?
Решение.
1)91-7=84 (книги) - уравняем количество книг на полках
2) 84:2=42 (книги) - на верхней полке
3) 42+7=49 (книг) - на нижней полке
Ответ: 42 и 49 книг
-
Тридцать животных - собак и кошек накормили котлетами. Каждая собака съела по три котлеты, а каждая кошка по две. Всего было съедено 73 котлеты. Сколько было собак и сколько кошек?
Решение.
Пусть все животные съели по две котлеты. Тогда бы всего съели 60 котлет. Тогда осталось бы лишних 73-60=13 котлет. То есть количество животных, которые съли по три котлеты - 13.
Ответ: собак было 13, кошек 17.
-
Мы отправились в поход на три дня. В первый день мы прошли много, но во второй день мы устали и прошли в два раза меньше, чем в первый день, а в третий день мы были совсем уставшие и прошли вдвое меньше, чем во второй день. Сколько мы проходили в каждый день, если весь маршрут составил 35 км.
Решение.
Пусть в третий день прошли одну часть пути, тогда во второй - две части пути, а в первый - 4. Всего весь путь составляет 7 частей и имеет протяженность 35 км.. Следовательно 35:7=5 км. - длина одной части пути или расстояние, которое прошли в третий день. Во второй день прошли 10 км, а в первый соответственно 20 км.
Ответ: 20, 10 и 5 км.
Метод общего кратного
-
Есть стог сена. Лошадь может съесть его за три дня, корова за два дня, а коза за шесть дней. За сколько дней они вместе съедят этот стог?
Решение.
Коза за 6 дней съест один стог, корова три стога, а лошадь два стога. Всего за шесть дней они съедят 6 стогов сена. То есть за один день они съедят один стог.
-
Летит стая драконов двух видов. У одних три головы и два хвоста, а у других две головы и три хвоста. Всего голов 173, а хвоста 192. Сколько трехголовых драконов в стае?
Решение.
1)173+192=365 (конечностей всего, то есть голов и хвостов)
2)365:5=73 - драконов в двух стаях
3)73 . 2=146 голов было бы, если все были бы двухголовые.
4)173-146=27 - трехголовых драконов
Задачи на сообразительность
-
На Солнечном острове живет 20 белых и 25 черных хамелеонов (хамелеоны - это животные, умеющие менять свой цвет). При встрече оба хамелеона меняют свой цвет на противоположный. Могут ли все хамелеоны окраситься в один цвет?
Решение
Да, могут. Например, если десять раз встретятся по парам белые хамелеоны и перекрасятся в черный цвет, тогда будет 45 черных хамелеонов.
-
В трех ящиках лежат орехи. В первом ящике на 6 кг орехов меньше, чем в двух других вместе. А во втором - на 10 кг меньше, чем в двух других вместе. Сколько орехов в третьем ящике?
Решение
Соединим оба заданных условия и получим следующее утверждение: "В первом и вором ящиках орехов на 6 кг+10 кг меньше, чем в первом, втором и двух третьих". Отсюда следует, что в двух третьих ящиках 16 кг орехов, т.е. в третьем ящике 8 кг орехов.
Глава III.
Решение текстовых задач в курсе старшей школы
Задачи на составление уравнений, или текстовые алгебраические задачи, изучаемые в старших классах можно условно классифицировать по типам:
-
задачи на числовые зависимости;
-
задачи, связанные с понятием «процента»;
-
задачи на прогрессии;
-
задачи на движение;
-
задачи на совместную работу;
-
задачи на смеси и сплавы.
Стандартная схема решения текстовой задачи состоит из нескольких этапов:
-
Обозначение буквами x, y, z, ... неизвестных величин, о которых идет речь в задаче.
-
Составление с помощью введенных переменных и известных из условия задачи величин уравнения или системы уравнений (в некоторых случаях - систем неравенств).
-
Решение полученного уравнения или системы уравнений.
-
Отбор решений, подходящих по смыслу задачи.
Выбирая неизвестные и составляя уравнения, мы создаем математическую модель ситуации, описанной в условии задачи. Это означает, что все соотношения должны следовать из конкретных условий задачи, то есть каждое условие должно быть представлено в виде уравнения (или неравенства).
Рассмотрим примеры решения некоторых типов задач из приведенной выше классификации, предварительно выделив особенности задач каждого типа, которые надо учитывать при их решении.
3.1 Задачи на движение
Уравнения, которые составляются на основании условий задач на движение, обычно содержат такие величины, как расстояние, скорости движущихся объектов, время, а также скорость течения воды (при движении по реке). При решении этих задач принимают следующие допущения:
-
Если нет специальных оговорок, то движение считается равномерным.
-
Повороты движущихся тел, переходы на новый режим движения считаются происходящими мгновенно.
-
Если тело с собственной скоростью х движется по реке, скорость течения которой равна у, то скорость движения тела по течению считается равной (х+у), а против течения - (х-у).
При решении задач на движение рекомендуется сделать рисунок, отображающий все условия задачи. При этом решающий задачу должен выбрать схему решения: какого вида уравнения составлять, то есть что сравнивать: время, затраченное на движение на отдельных участках пути, или пройденный каждым объектом путь.
При решении задач такого типа часто необходимо узнать время встречи двух объектов, начинающих движение одновременно из двух точек с разными скоростями и движущихся навстречу друг другу либо в случае, когда один объект догоняет другой.
П усть расстояние между точками А и В равно S. Два тела начинают движение одновременно, но имеют разные скорости v1 и v2. Пусть С - точка встречи, а t - время движения тел до встречи. В случае движения навстречу друг другу имеем АС=v1t, BC=v2t. Сложим эти два равенства:
усть расстояние между точками А и В равно S. Два тела начинают движение одновременно, но имеют разные скорости v1 и v2. Пусть С - точка встречи, а t - время движения тел до встречи. В случае движения навстречу друг другу имеем АС=v1t, BC=v2t. Сложим эти два равенства:
АС+СВ=v1t+v2t=(v1+v2)t Þ AB=S=(v1+v2)t Þ  .
.
Если одно тело догоняет другое, то теперь получаем АС=v1t, BC=v2t. Вычтем эти равенства:
А С-ВС=(v1-v2)t.
С-ВС=(v1-v2)t.
Так как АС-ВС=AB=S, то время, через которое первое тело догонит второе, определяется равенством
![]() .
.
Задача 1. Пароход прошел 4 км против течения реки, а затем прошел еще 33 км по течению, затратив на весь путь один час. Найдите собственную скорость парохода, если скорость течения реки равна 6,5 км/ч.
Решение:
Пусть х км/ч - собственная скорость парохода.
Тогда (х+6,5) км/ч - скорость парохода по течению.
(х-6,5) км/ч - скорость парохода против течения.
Так как против течения пароход прошел 4 км со скоростью (х-6,5) км/ч, то
![]() ч. - время движения парохода против течения.
ч. - время движения парохода против течения.
Так как по течению пароход прошел 33 км со скоростью (х+6,5) км/ч, то
![]() ч. - время движения парохода по течению.
ч. - время движения парохода по течению.
По условию ![]()
решим полученное уравнение
![]()
![]()
Откуда получаем квадратное уравнение
х2-37х+146,25=0 Þ х1=4,5 км/ч и х2=32,5 км/ч.
Осуществим отбор полученных решений.
Через х мы обозначили собственную скорость парохода, при этом скорость течения реки 6,5 км/ч, поэтому х1=4,5 км/ч не подходит по смыслу задачи (при такой скорости пароход не выплыл бы против течения).
Поэтому, собственная скорость парохода равна 32,5 км/ч.
Ответ: v=32,5 км/ч.
Задача 2. Расстояние между городами А и В равно 60 км. Два поезда выходят одновременно: один из А в В, другой из В в А. Пройдя 20 км, поезд, идущий из А в В, останавливается на полчаса, затем, пройдя 4 минуты, встречает поезд, идущий из В. Оба поезда прибывают к месту назначения одновременно. Найдите скорости поездов.
Решение:
О
4 мин.тобразим все условия задачи на рисунке.
Заметим, что если время в условии задачи выражено как в часах, так и в минутах, то минуты надо перевести в часы. В нашем случае 4 мин=4/10 часа=1/15 часа.
Так как в задаче надо определить две величины, введем две переменные и составим два уравнения.
Пусть х км/ч - скорость поезда, вышедшего из пункта А;
у км/ч - скорость поезда, вышедшего из пункта В.
Так как в задаче известно расстояние, выразим время через скорость и расстояние.
![]() - время, за которое поезд из А прошел 20 км.
- время, за которое поезд из А прошел 20 км.
![]() - время, затраченное поездом из А до встречи в пункте D.
- время, затраченное поездом из А до встречи в пункте D.
![]() - расстояние, которое прошел поезд из А за 4 минуты после остановки.
- расстояние, которое прошел поезд из А за 4 минуты после остановки.
Тогда поезд из А до встречи в пункте D прошел ![]() км.
км.
![]() км - расстояние, пройденное поездом из В до встречи.
км - расстояние, пройденное поездом из В до встречи.
![]() - время, пройденное поездом из В до встречи в пункте D.
- время, пройденное поездом из В до встречи в пункте D.
Так как по условию в пункте D поезда встретились, они затратили на путь до встречи одинаковое время, поэтому получаем первое уравнение
 .
.
С другой стороны, выразим время движения поездов после встречи в пункте D.
Так как ![]() , то
, то  - время движения поезда из В после встречи.
- время движения поезда из В после встречи.
Так как ![]() , то
, то  - время движения поезда из А после встречи.
- время движения поезда из А после встречи.
По условию  .
.
Таким образом, мы составили систему двух уравнений с двумя переменными.

Решим систему, для чего из первого уравнения выразим у и подставим это выражение вместо у во второе уравнение.
 ;
;
 ;
;
 .
.
Решим полученное уравнение
![]() ;
;
![]() ;
;
![]() ;
;
х1=60; х2=-600.
Так как х - скорость, то х2 не подходит по смыслу задачи. Подставим полученное значение х в выражение для у
 .
.
Ответ: vA=60 км/ч, vB=40 км/ч.
Фон Нейман и задача о мухе. Эту задачу можно решить двумя способами: "трудным" и "легким".
Два поезда, находившиеся на расстоянии 200 км друг от друга, сближаются по одной колее, причем каждый развивает скорость 50 км/ч. С ветрового стекла одного локомотива в начальный момент движения взлетает муха и принимается летать со скоростью 75 км/ч вперед и назад между поездами, пока те, столкнувшись, не раздавят ее. Какое расстояние успевает пролететь муха до столкновения?
С каждым из поездов муха успевает повстречаться бесконечно много раз. Чтобы найти расстояние, которое муха преодолела в полете, можно просуммировать бесконечный ряд расстояний (эти расстояния убывают достаточно быстро, и ряд сходится). Это - "трудное" решение. Чтобы получить его, вам понадобятся карандаш и бумага. "Легкое" решение состоит в следующем. Поскольку в начальный момент расстояние между поездами равно 200 км, а каждый поезд развивает скорость 50 км/ч, то от начала движения до столкновения проходит 2 ч. Все эти 2 ч муха находится в полете. Поскольку она развивает скорость 75 км/ч, то до того момента, как столкнувшиеся локомотивы раздавят ее, муха успеет пролететь 150 км. Вот и все!
Один из выдающихся математиков современности, Джон фон Нейман, когда ему задали эту задачу, задумался лишь на миг и сказал: "Ну, конечно, 150 км!" Приятель спросил его: "Как вам удалось так быстро получить ответ?" "Я просуммировал ряд", - ответил математик.
Задачи на движение
Во всех таких задачах допускается определенная идеализация: считается, что тела движутся прямолинейно и равномерно, скорости (в том числе скорость течения) постоянны в течение определенных промежутков времени, не меняются при поворотах и т.д., движущиеся тела считаются материальными точками (если не оговорено противное), т.е. не имеющими размеров и массы (вернее, их размеры и масса несущественны для решения задачи). Даже решение задач на движение по окружности не требует применения специальных понятий - угловой скорости и т.п.; здесь точнее было бы говорить о движении по замкнутой трассе. Если расстояние между пунктами, из которых начинают движение два тела, не задано, иногда бывает удобно положить его равным единице. При решении задач на движение двух тел часто очень удобно считать одно тело неподвижным, а другое - приближающимся к нему со скоростью, равной сумме скоростей этих тел (при движении навстречу) или разности скоростей (при движении вдогонку). Такая модель помогает разобраться с условием задачи, получить нужные уравнения даже в таком относительно трудном случае, как движение по окружности.
Основными типами задач на движение являются следующие:
1) задачи на движение по прямой (навстречу и вдогонку),
2) задачи на движение по замкнутой трассе,
3) задачи на движение по воде,
4) задачи на среднюю скорость,
5) задачи на движение протяженных тел.
Рассмотрим более подробно каждый из этих типов задач, выделив, где необходимо, базовые задачи.
Движение навстречу.
Если расстояние между двумя телами равно s, а их скорости ![]() и
и ![]() то время t, через которое они встретятся, находится по формуле:
то время t, через которое они встретятся, находится по формуле:
![]()
Движение вдогонку
Если расстояние между двумя телами равно s, они движутся по прямой в одну сторону со скоростями ![]() и
и ![]() соответственно (
соответственно (![]() >
> ![]() ) так, что первое тело следует за вторым, то время t, через которое первое тело догонит второе, находится по формуле
) так, что первое тело следует за вторым, то время t, через которое первое тело догонит второе, находится по формуле
![]()
Задача 1. Два пешехода отправляются в одном направлении одновременно из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго.
Через сколько минут расстояние между пешеходами станет равным 300 метрам?
Решение.
Время t в часах, за которое расстояние между пешеходами станет равным 300 метрам, т.е. 0,3 км, находим по формуле t = 0,3 : 1,5 = 0,2 (ч)
Следовательно, это время составляет 12 минут.
Ответ: через 12 минут.
Задачи на среднюю скорость
Задача2. на среднюю скорость( учебное пособие «Математика-9 класс»Дорофеев Г.В. стр 67)
Первую половину пути автомобиль проехал со скоростью 90км/ч, а вторую со скоростью 60 км/ч. Найти среднюю скорость движения автомобиля.
В 99 случаях дают учащиеся ответ: к75м/ч. И на мой наивный вопрос - "почему?"- слышу вполне разумный довод о среднем арифметическом.
Предлагаю довести ситуацию до абсурда: допустим, что вторую половину пути автомобиль ехал со скоростью, едва отличной от нуля. Тогда среднее арифметическое (90+0)/2 = 45 (км/ч). Но ведь автомобиль вторую половину пути и вовсе не ехал, и его средняя скорость должна быть нулевой. Как же решать эту задачу?
Средняя скорость есть отношение всего пройденного пути ко всему затраченному времени:
![]()
![]() время, затраченное на первую половину пути,
время, затраченное на первую половину пути, ![]() на вторую половину пути. Тогда время, затраченное на каждую половину пути, определяется как отношение половины пути к скорости на каждом участке:
на вторую половину пути. Тогда время, затраченное на каждую половину пути, определяется как отношение половины пути к скорости на каждом участке:
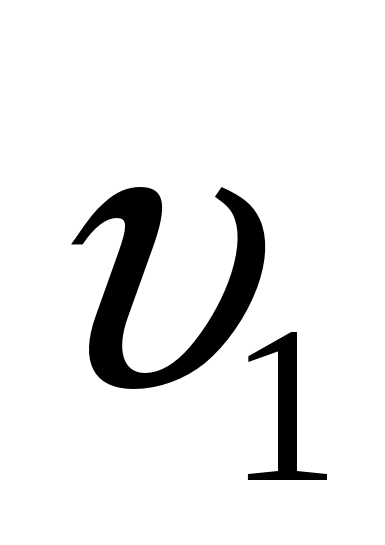
Подставив это в исходную формулу средней скорости, будем иметь:
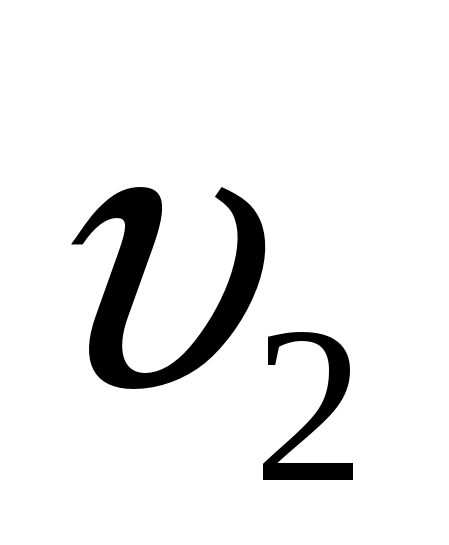
Таким образом, окончательная формула определение средней скорости:
![]()
И в нашем случае мы получим 72 км/ч. А почему не 75? А потому, что двигаясь с меньшей скоростью, автомобиль потратил на вторую половину пути больше времени, и ![]() средняя скорость движения всегда меньше среднего арифметического.
средняя скорость движения всегда меньше среднего арифметического.
Задача 3. (открытый банк данных)
Первый час автомобиль ехал со скоростью 120 км/ч, 2 часа со скоростью 85 км/ч,2 часа со скоростью 80 км/ч. Найти среднюю скорость.
Занесем все данные в таблицу
V(км/ч)
t(ч)
S(км)
I
120
1
120
II
85
2
170
III
80
2
160
Решение: ![]() ;
;
![]() ;
;
![]()
Ответ:90 км/ч.
Задача 4
Первую треть пути автомобиль ехал со скоростью 40 км/ч, вторую треть со скоростью 60км/ч, и третью треть со скоростью 80 км/ч. Определить среднюю скорость движения.
Занесем эти данные в таблицу:
V(км/ч)
t(ч)
S(км)
I
40
![]()
![]() S
S
II
60
![]()
![]() S
S
III
80
![]()
![]() S
S
Решение
![]() ;
;

Задача 5.(Тренировочная работа по математике 9 класс от 19.12.2011)
Пристани А и В расположены на реке, скорость течения которой на этом участке равна 4 км/ч .Лодка проходит от А до В и обратно без остановок со средней скоростью 6 км/ч. Найдите собственную скорость лодки.
Занесем эти данные в таблицу:
Vл(км/ч)
Vр(км/ч)
V(км/ч)
t(ч)
S(км)
По течению
х
4
Х+4
![]()
S
Против течения
х
4
Х-4
![]()
S
Первый способ.
![]() ;
; 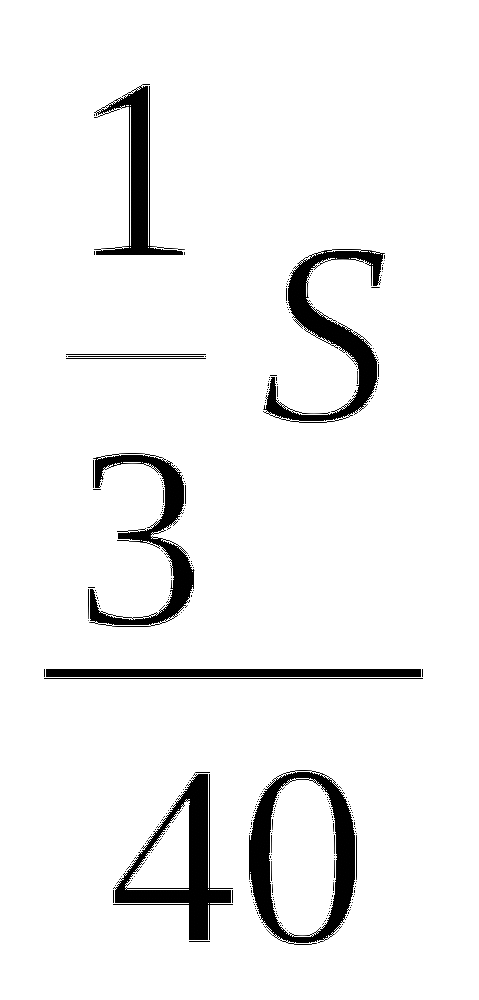 ;
;
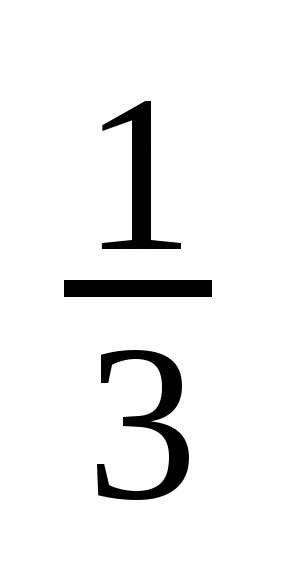 ;
;
![]()
![]()
![]()
-2 не подходит по условию.
Значит скорость лодки 8 км/ч.
Ответ: 8 км/ч.
Второй способ.
Воспользуемся формулой из задачи 1.
![]()
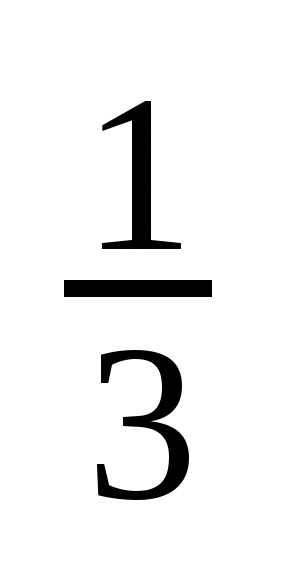
Ответ : 8 км/ч
Рассмотрим движение двух точек по окружности длины s в одном направлении при одновременном старте со скоростями v1 и v2 (v1 > v2 ) и ответим на вопрос: через какое время первая точка будет опережать вторую ровно на один круг? Считая, что вторая точка покоится, а первая приближается к ней со скоростью v1 - v 2., получим, что условие задачи будет выполнено, когда первая точка поравняется в первый раз со второй. При этом первая точка пройдет расстояние, равное длине одного круга, и искомая формула ничем не отличается от формулы, полученной для задачи на движение вдогонку:
![]()
Итак, если две точки одновременно начинают движение по окружности в одну сторону со скоростями v1 и v2 соответственно (v1 > v2 соответственно), то первая точка приближается ко второй со скоростью v1 - v2 и в момент, когда первая точка в первый раз догоняет вторую, она проходит расстояние на один круг больше.
Задача 6.(открытый банк данных)
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение. Пусть скорость второго автомобиля х км/ч.
Составим таблицу
V(км/ч)
t(ч)
S(км)
I
80
14
II
х
Поскольку 40 минут составляют 2/3 часа и это - то время, за которое первый автомобиль будет опережать второй на один круг, составим по условию задачи уравнение
![]()
откуда 160 - 2х = 42, т. е. х = 59.
Ответ. 59 км/ч
Рассуждения можно проводить и следующим способом.
Задача 7 (открытый банк данных)
Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на 1 круг. За сколько минут второй лыжник проходит один круг?
Решение.
Пусть длина окружности равна S метров (в этой задаче и спорте её называют круговой лыжней и кругом).
Пусть первый лыжник проходит 1 круг за х минут, тогда второй - за( х+2) минуты. Скорость первого лыжника ![]() м/мин, а второго
м/мин, а второго![]() м/мин.
м/мин.
Составим таблицу №1
V(м/мин)
t(мин)
S(м)
I
![]()
х
S
II
![]()
х+2
S
Составим таблицу №2
За 1 час первый проходит ![]() метров, а второй
метров, а второй ![]() метров.
метров.
V(м/мин)
t(мин)
S(м)
I
![]()
60
![]()
II
![]()
60
![]()
А т.к. первый проходит на 1 круг больше, т.е. на S метров, то получаем уравнение:
![]() -
-![]() = S, (разделим обе части на S)
= S, (разделим обе части на S)
![]() -
-![]() =1; x2 + 2x - 120 = 0;
=1; x2 + 2x - 120 = 0;
х1=10 (х2 = -12 не удовл. усл.)
Первый проходит круг за 10 минут, а второй за 12.
Ответ: 12.
Задача 8(открытый банк данных)
Два тела движутся по окружности в одну сторону. Первое проходит на 3 минуты быстрее второго и догоняет второе каждые полтора часа. За сколько минут первое тело проходит один круг?
Решение. Пусть длина окружности S
Пусть первое тело проходит 1 круг за t минут, тогда за 1 минуту тело проходит путь ![]() аналогично второе - за минуту
аналогично второе - за минуту ![]() .
.
Составим таблицу №1
V(м/мин)
t(мин)
S(м)
I
![]()
t
S
II
![]()
t+3
S
за 90 минут первое - ![]() второе -
второе - ![]()
Составим таблицу №2
V(м/мин)
t(мин)
S(м)
I
![]()
90
![]()
II
![]()
90
![]()
Составим уравнение, учитывая, что первый догоняет второго каждые полтора часа
![]() =
=![]() +S;
+S;
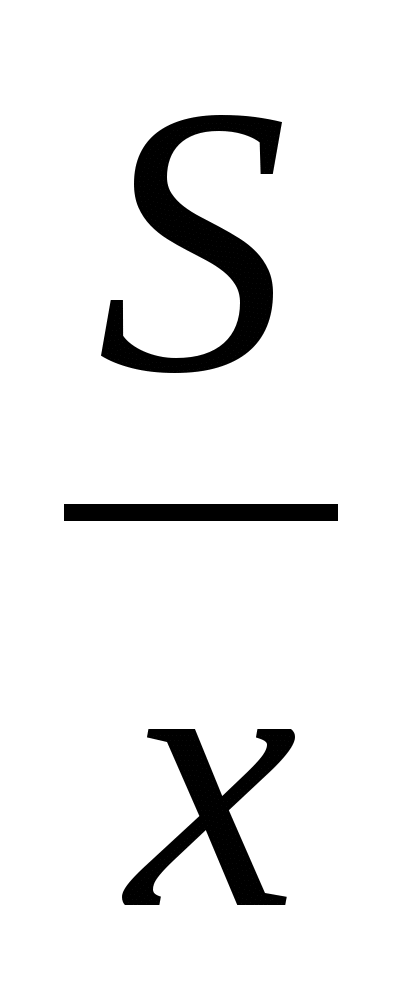
-18 -не подходит по условию задачи.
Ответ: 15 км/ч.
Задача9 на движение по реке (открытый банк данных)
Расстояние между пристанями А и В равно 48 км. Отчалив от пристани А в 10 часов утра, теплоход проплыл по течению реки с постоянной скоростью до пристани В. После трехчасовой стоянки у пристани В теплоход отправился в обратный рейс и прибыл в А с тот же день в 22.00. Найдите скорость теплохода в неподвижной воде, если скорость течения реки равна 4 км/ч.
Решение.
Это стандартная задача на движение по реке.
Обозначим собственную скорость теплохода х км/ч. Тогда его скорость по течению реки будет (х+4) км.ч, а против течения (х-4) км/ч.
Запишем эти данные в таблицу:
vл(км/ч)
vр(км/ч)
v(км/ч)
t(ч)
S(км)
По течению
х
4
x+4
![]()
48
Против течения
х
4
x-4
![]()
48
Время движения от А до В, т.е. по течению равно ![]() , а против течения равно
, а против течения равно ![]() складывая время движения теплохода туда и обратно со временем стоянки - 3 часа, получим
складывая время движения теплохода туда и обратно со временем стоянки - 3 часа, получим
![]() +
+ ![]() + 3, что равно 22.00-10.00=12 часов.
+ 3, что равно 22.00-10.00=12 часов.
Решим уравнение ![]() +
+ ![]() +3 = 12 ; 48(x-4) + 48(х+4) =9(х+4)(х-4) ;
+3 = 12 ; 48(x-4) + 48(х+4) =9(х+4)(х-4) ;
16(х-4) + 16(х+4) = 3(х2 - 16); 3x2 - 32x -48 =0.
D=1600, х1= (32+40)/6 = 12, х2= (32-40)/6 <0 - не удовл. усл. задачи.
Ответ: 12 км/ч.
Задача10 (открытый банк данных)
Два автомобиля выезжают из двух пунктов навстречу друг другу и после встречи продолжают путь. После встречи первый прибывает в пункт назначения через 25 часов, а второй через 36 часов. Первый автомобиль движется со скоростью на 10 км в час больше чем второй. Найти скорость второго автомобиля.
A________________________B___________C
Пусть скорость второго х км/ч, первого автомобиля (х+10).
Пусть встреча произошла через t часов в пункте В. Тогда АВ =t(x+10), СВ= tx. До встречи
v(км/ч)
t(ч)
S(км)
I
x+10
t
t(x+10)
II
x
t
tx
После встречи: первый прошел путь ВС=25(х+10), а второй ВА=36х.
v(км/ч)
t(ч)
S(км)
I
x+10
25
25(x+10)
II
x
36
36x
Т.к. АВ=ВА и СВ=ВС, то составим систему уравнений:
t(x+10) = 36x (1)
tx = 25(x+10) (2)
Раскрыть скобки и из (1) вычесть (2).
10t = 11x - 250; t= 1,1x - 25. Подставим t в (2), получим квадратное уравнение:
1,1х2 - 50х -250 =0.
х=50 - скорость второго автомобиля, х+10=60 - скорость первого.
Ответ: 60 км/ч
Задачи на движение протяженных тел
В задачах на движение протяжных тел требуется определить длину одного из них. Наиболее типичные ситуации: определение длины поезда проезжающего мимо
-
придорожного столба
-
идущего параллельно путям пешехода
-
лесополосы определенной длины
-
другого двигающегося поезда
Если поезд движется мимо столба, то он проходит расстояние равное его длине. Если поезд движется мимо протяженной лесополосы, то он проходит расстояние равное сумме длины самого поезда и лесополосы.
Задача 11. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.
Р![]() ешение: Зная скорость движения v = 60 км/ч = и время, за которое он проезжает мимо столба t = 30 сек. =
ешение: Зная скорость движения v = 60 км/ч = и время, за которое он проезжает мимо столба t = 30 сек. =
v(км/ч)
t(ч)
S(км)
I
60
![]()
-
.
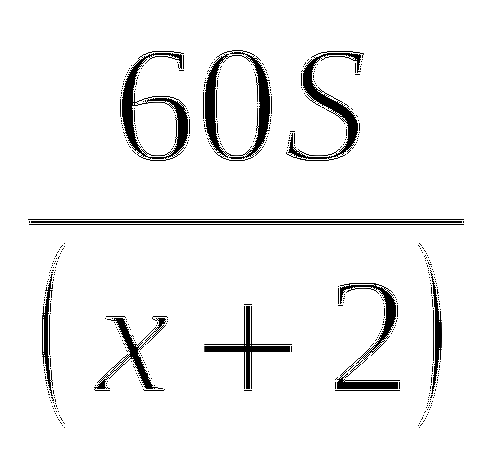
можно найти длину поезда как пройденное расстояние s = vt ==60.![]() =0,5км=500 м.
=0,5км=500 м.
Ответ: 500 м
Задача 12(открытый банк данных)
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо лесополосы, длина которой равна 600 метров, за 36 секунд. Найдите длину поезда в метрах.
Решение.
600м=0,6км
Обозначим за х(м)-длину поезда
v(км/ч)
t(ч)
S(км)
I
80
![]()
х+0,6
Учитывая, что время движения 36 секунд= 0,01 ч, составим уравнение
![]() =0,01
=0,01
0,6+х=0,8; х=0,2(км)
0,2 км=200 метров
Ответ : 200 метров
Задача 13(открытый банк данных)
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 85 км/ч и 50 км/ч. Длина пассажирского поезда равна 600 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Решение.
Обозначим длину скорого поезда х км/ч.
Скорый проходит путь: (0,6+х)км.
Скорость скорого относительно пассажирского :85+50=135(км/ч)
V(км/ч)
t(ч)
S(км)
скорый
135
![]()
x+0,6
![]() =0,01
=0,01
0,6+х=1,35; х=0,75(км)
Ответ:750 метров
3.2 Задачи на производительность
Содержание задач этого типа сводится обычно к следующему: некоторую работу, объем которой не указывается и не является искомым, выполняют несколько человек или механизмов, работающих равномерно, то есть с постоянной для каждого из них производительностью. В таких задачах объем всей работы, которая должна быть выполнена, принимается за 1; время t, требующееся для выполнения всей работы, и р - производительность труда, то есть объем работы, сделанной за единицу времени, связаны соотношением
![]() .
.
Рассмотрим стандартную схему решения задач этого типа.
Пусть х - время выполнения некоторой работы первым рабочим,
у - время выполнения этой же работы вторым рабочим.
Тогда ![]() - производительность труда первого рабочего,
- производительность труда первого рабочего,
![]() - производительность труда второго рабочего.
- производительность труда второго рабочего.
![]() - совместная производительность труда.
- совместная производительность труда.
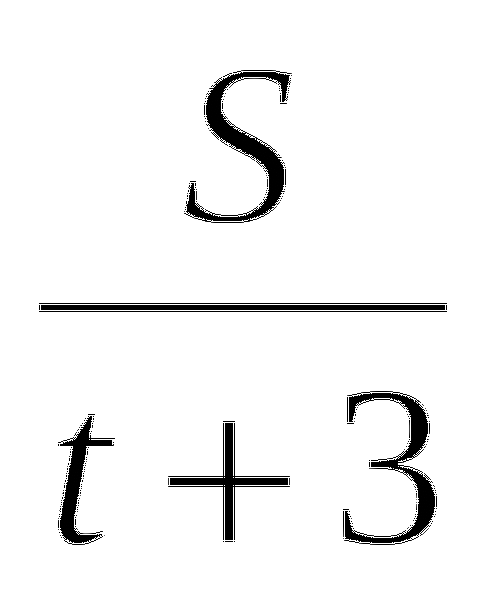 - время, за которое они выполнят задание, работая вместе.
- время, за которое они выполнят задание, работая вместе.
Задача 1. Двое рабочих выполняют некоторую работу. После 45 минут совместной работы первый рабочий был переведен на другую работу, и второй рабочий закончил оставшуюся часть работы за 2 часа 15 минут. За какое время мог бы выполнить работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 час больше, чем первому.
Решение:
Пусть х - время работы первого по выполнению всей работы.
у - время работы второго рабочего.
По условию х=у-1, и первое уравнение составлено.
Пусть объем всей работы равен 1.
Тогда ![]() - производительность труда первого рабочего,
- производительность труда первого рабочего,
![]() - производительность труда второго рабочего.
- производительность труда второго рабочего.
Так как они работали 45 мин.=3/4 часа совместно, то
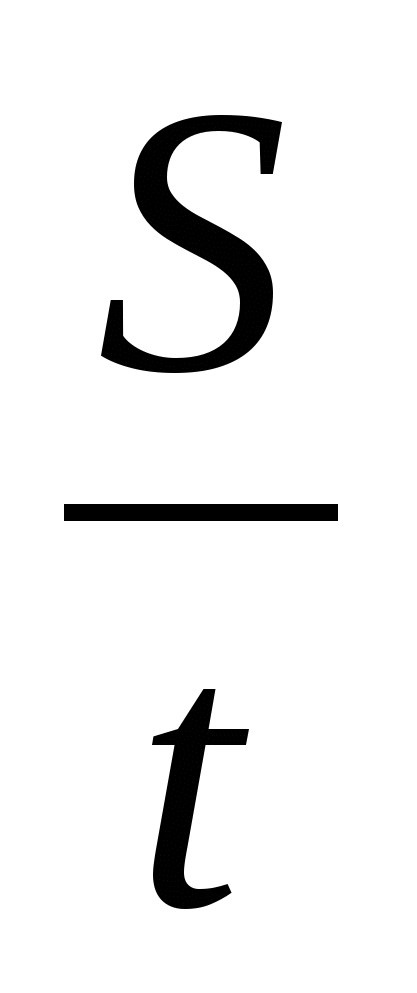 - объем работы, выполненной рабочими за 45 минут.
- объем работы, выполненной рабочими за 45 минут.
Так как второй рабочий работал один 2 часа 15 минут=2¼=9/4 часа, то
![]() - объем работы, выполненной вторым рабочим за 2 часа 15 минут.
- объем работы, выполненной вторым рабочим за 2 часа 15 минут.
По условию 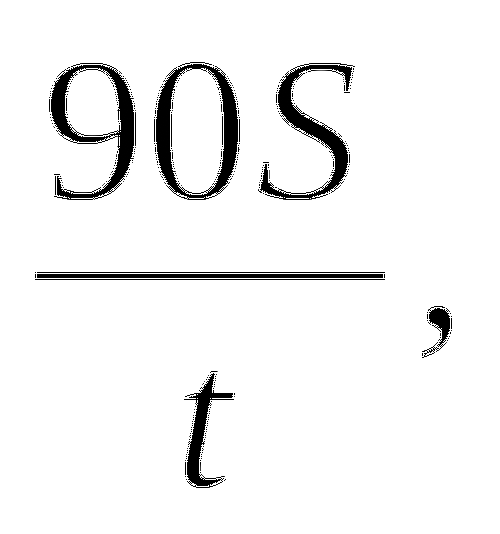 .
.
Таким образом, мы получили систему двух уравнений
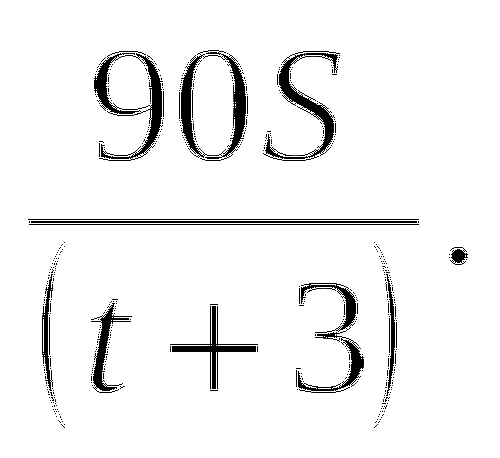
Решим ее, для этого выражение для х из первого уравнения подставим во второе
![]() Þ
Þ ![]() Þ 4у2-19у+12=0
Þ 4у2-19у+12=0
![]() ч. и у2=4 ч.
ч. и у2=4 ч.
Из двух значений для у выберем то, которое подходит по смыслу задачи у1=45 мин., но 45 мин. рабочие работали вместе, а потом второй рабочий работал еще отдельно, поэтому ![]() не подходит по смыслу задачи. Для полученного у2=4 ч. найдем из первого уравнения первоначальной системы значение х
не подходит по смыслу задачи. Для полученного у2=4 ч. найдем из первого уравнения первоначальной системы значение х
х=4-1 Þ х=3 ч.
Ответ: первый рабочий выполнит работу за 3 часа, второй - за 4 часа.
Замечание: эту задачу можно было решить, не вводя вторую переменную у, а выразить время работы второго рабочего через х, тогда нужно было составить одно уравнение и решить его.
Задача 2. Две бригады рабочих начали работу в 8 часов. Сделав вместе 72 детали, они стали работать раздельно. В 15 часов выяснилось, что за время раздельной работы первая бригада сделала на 8 деталей больше, чем вторая. На другой день первая бригада делала за 1 час на одну деталь больше, а вторая бригада за 1 час на одну деталь меньше. Работу бригады начали вместе в 8 часов и, сделав 72 детали, снова стали работать раздельно. Теперь за время раздельной работы первая бригада сделала на 8 деталей больше, чем вторая, уже к 13 часам. Сколько деталей в час делала каждая бригада?
Решение:
Пусть х деталей в час изготовляет первая бригада (производительность первой бригады).
у - производительность второй бригады.
х+у - совместная производительность бригад.
Так как вместе они сделали 72 детали, то
![]() - время совместной работы бригад.
- время совместной работы бригад.
Так как бригады работали с 8 до 15 часов, всего 7 часов, то
![]() - время работы бригад раздельно, тогда
- время работы бригад раздельно, тогда
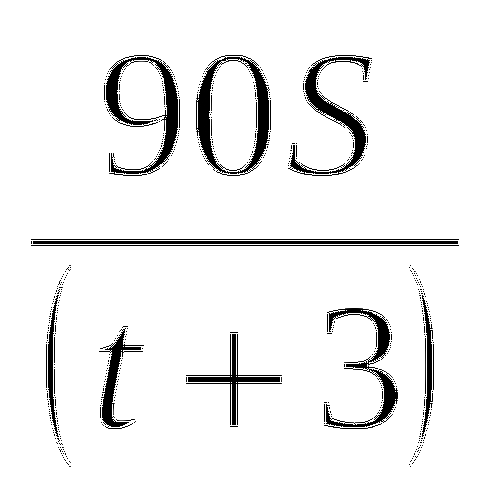 - число деталей, которое изготовила первая бригада, работая отдельно
- число деталей, которое изготовила первая бригада, работая отдельно
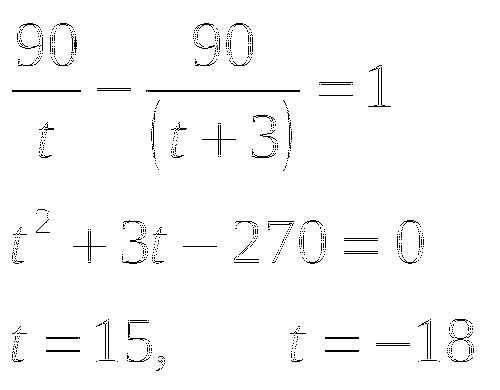 - число деталей, которое изготовила вторая бригада, работая отдельно
- число деталей, которое изготовила вторая бригада, работая отдельно
По условию 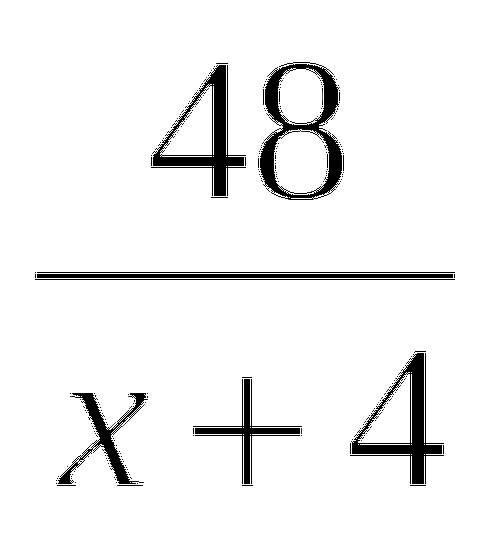 или
или 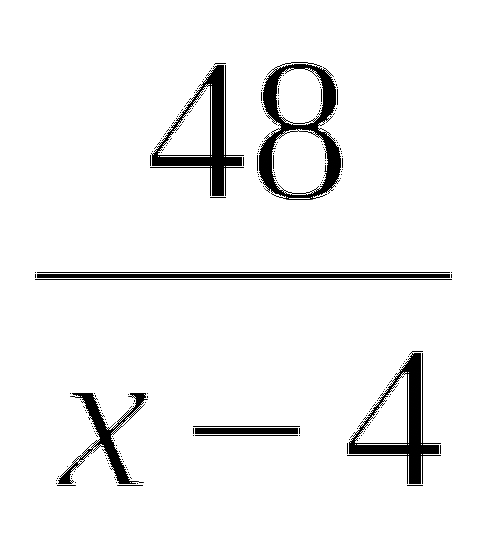
Составим второе уравнение. По условию:
х+1 - производительность труда первой бригады на другой день.
у-1 - производительность труда второй бригады на другой день.
х+1+у-1=х+у - совместная производительность (такая же, как и в первый день).
Так как бригады работали с 8 до 13 часов - всего 5 часов, то
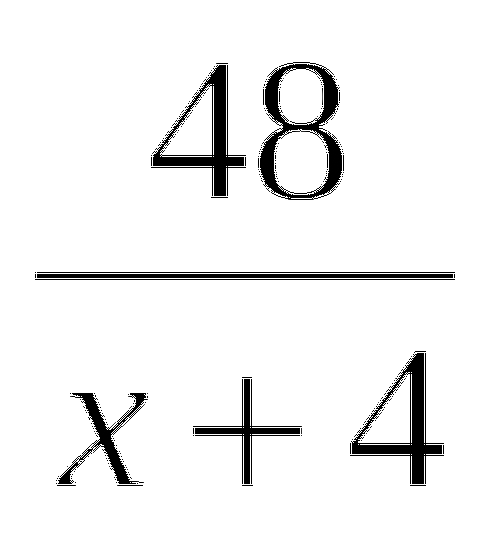 - число деталей, которые изготовила первая бригада, работая отдельно, во второй день.
- число деталей, которые изготовила первая бригада, работая отдельно, во второй день.
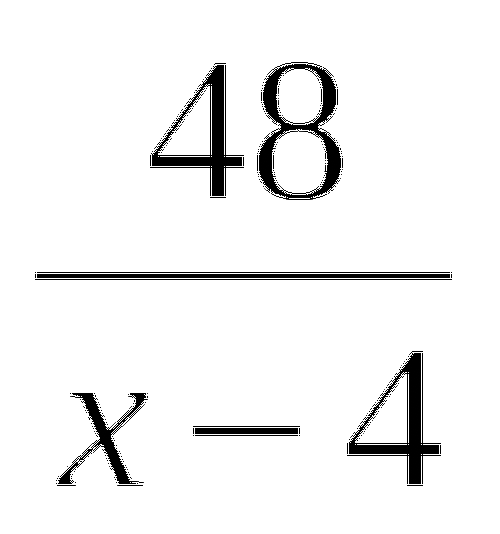 - число деталей, которые изготовила вторая бригада, работая отдельно, во второй день.
- число деталей, которые изготовила вторая бригада, работая отдельно, во второй день.
По условию 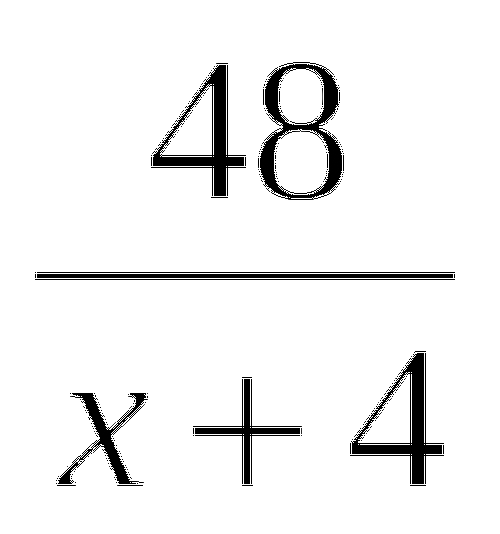 или
или 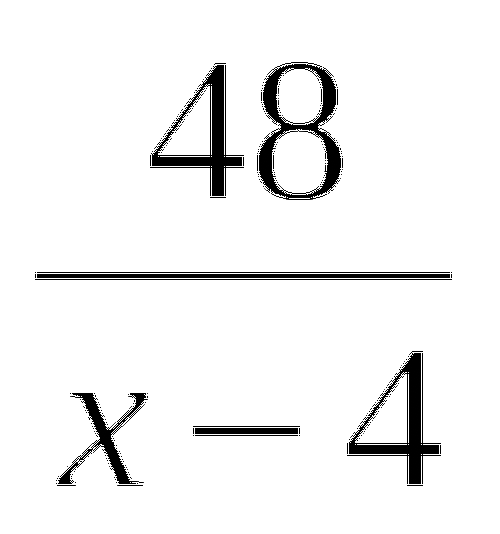 .
.
Таким образом, мы составили систему двух уравнений:
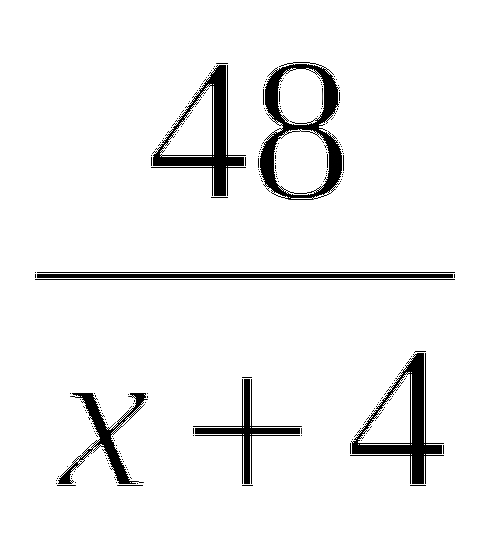
Решим эту систему методом замены переменных:
Пусть ![]() ...................(V)
...................(V)
Тогда имеем:
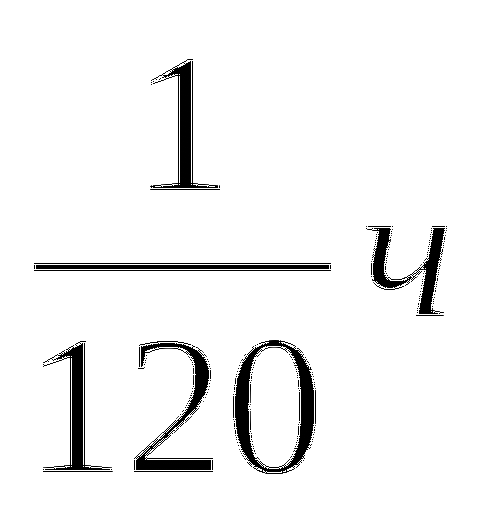 Þ
Þ 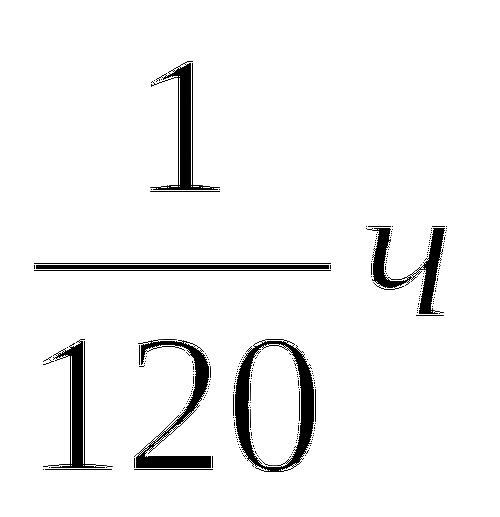
Выразим из первого уравнения ![]() и подставим во второе уравнение
и подставим во второе уравнение
![]() Þ v2+2v-8=0 Þ v1=2, v2=-4.
Þ v2+2v-8=0 Þ v1=2, v2=-4.
Значение v2=-4 не подходит по смыслу задачи (из условия ясно, что производительность первой бригады выше, чем второй, а значит х-у=v>0). Найдем значение u, соответствующее v2=2, подставив значение v2 в выражение для u:
![]() .
.
Так как нам нужно найти значения х и у, подставим полученные значения для u и v в (V)
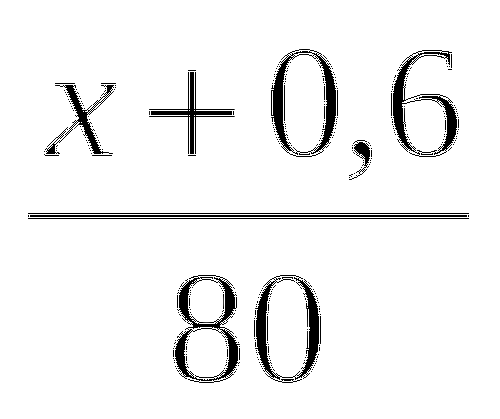 Þ
Þ 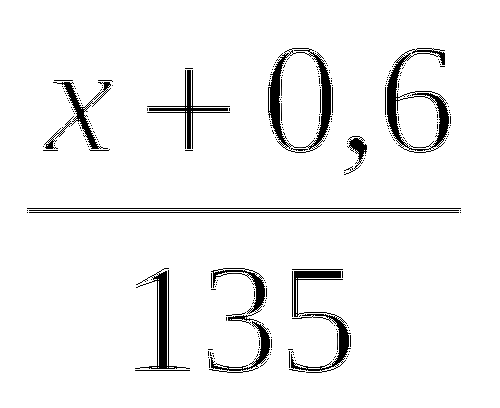 Þ
Þ 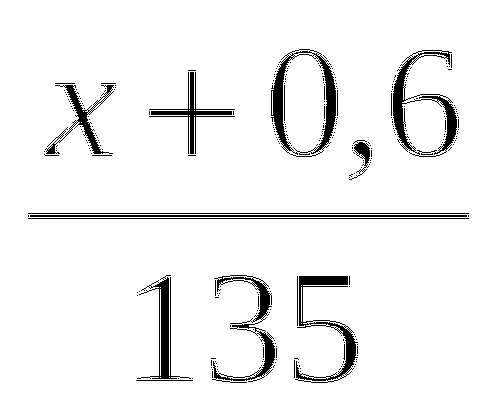 Þ
Þ  Þ
Þ 
Ответ: 13 деталей в час изготавливала первая бригада; 11 деталей в час изготавливала вторая бригада.
3.3 Задачи на проценты
Решение задач этого типа тесно связано с тремя алгоритмами: нахождения части от целого, восстановление целого по его известной части, нахождение процентного прироста. Рассмотрим эти алгоритмы.
-
Пусть известна некоторая величина А, надо найти а % этой величины.
Если считать, что А есть 100%, а неизвестная часть х это а %, то из пропорции
![]() имеем
имеем ![]() .
.
-
Пусть известно, что некоторое число b составляет а % от неизвестной величины А. Требуется найти А.
Рассуждая аналогично, из пропорции получаем ![]() .
.
-
Пусть некоторая переменная величина А, зависящая от времени t, в начальный момент t0 имеет значение А0, а в момент t1 - значение А1.
Тогда абсолютный прирост величины А за время t1-t0 будет равен А1-А0; относительный прирост этой величины вычисляется по формуле ![]() , а процентный прирост по формуле
, а процентный прирост по формуле ![]() .
.
Задача 1. Для офиса решили купить 4 телефона и 3 факса на сумму 1470 долларов. Удалось снизить цену на телефон на 20%, и в результате за эту же покупку уплатили 1326 долларов. Найти цену факса.
Решение:
Пусть х - стоимость факса,
у - стоимость телефона.
По условию 4у+3х=1470.
Так как цену на телефон снизили на 20%, то телефон стал стоить 80% от первоначальной цены, то есть
0,8у - стоимость телефона после снижения.
По условию 3х+4×0,8у=1326.
Решим полученную систему двух уравнений методом алгебраического сложения.

Так как нам нужно найти только х, исключим у из системы, для чего первое уравнение умножим на (-0,8) и сложим со вторым: 0,6х=150 Þ х=250.
Ответ: факс стоит 250 долларов.
3.4 Задачи на смеси и сплавы
В задачах этого типа основным является понятие «концентрация». Что же это такое?
Рассмотрим, например, раствор кислоты в воде. Пусть в сосуде содержится 10 литров раствора, который состоит из 3 литров кислоты и 7 литров воды. Тогда относительное (по отношению ко всему объему) содержание кислоты в растворе равно ![]() . Это число и определяет концентрацию кислоты в растворе. Иногда говорят о процентном содержании кислоты в растворе. В приведенном примере процентное содержание будет таково:
. Это число и определяет концентрацию кислоты в растворе. Иногда говорят о процентном содержании кислоты в растворе. В приведенном примере процентное содержание будет таково: ![]() . Как видно, переход от концентрации к процентному содержанию и наоборот весьма прост.
. Как видно, переход от концентрации к процентному содержанию и наоборот весьма прост.
Итак, пусть смесь массы М содержит некоторое вещество массой m. Тогда:
-
концентрацией данного вещества в смеси (сплаве) называется величина
 ;
; -
процентным содержанием данного вещества называется величина с×100%;
Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=c×M.
Задачи на смеси (сплавы) можно разделить на два вида:
-
Задаются, например, две смеси (сплава) с массами m1 и m2 и с концентрациями в них некоторого вещества, равными соответственно с1 и с2. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c1m1+c2m2, а концентрация
 .
. -
Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.
При решении таких задач необходимо установить контроль за количеством данного вещества и его концентрацией при каждом отливе, а также при каждом доливе смеси. В результате такого контроля получаем разрешающее уравнение. Рассмотрим конкретные задачи.
Задача 1. Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?
Решение:
Пусть х кг олова надо добавить к сплаву. Так как процентное содержание меди в сплаве равно 45 %, то масса меди в первоначальном сплаве m=0,45×12=5,4 кг (где 0,45 - концентрация меди в сплаве).
Тогда 12+х - масса нового сплава
И так как масса меди в первоначальном сплаве равна 5,4 кг, то
![]() - концентрация меди в новом сплаве.
- концентрация меди в новом сплаве.
По условию ![]() , решая уравнение, получаем х=1,5 кг.
, решая уравнение, получаем х=1,5 кг.
Ответ: нужно добавить 1,5 кг чистого олова.
Задача 2. Имеются два раствора кислоты разной концентрации. Объем одного раствора 4 л, другого - 6 л. Если их слить вместе, то получится 35 % раствор кислоты. Если же слить равные объемы этих растворов, то получится 36 % раствор кислоты. Сколько литров кислоты содержится в каждом из первоначальных растворов?
Решение:
Пусть х л кислоты содержится в первом растворе,
у л кислоты содержится во втором растворе.
Тогда ![]() - концентрация кислоты в первом растворе,
- концентрация кислоты в первом растворе,
![]() - концентрации кислоты во втором растворе.
- концентрации кислоты во втором растворе.
Если слить два раствора, то получим раствор массой 4л+6л=10л, причем масса кислоты в нем будет х+у, тогда
![]() - концентрация кислоты, после сливания обоих растворов.
- концентрация кислоты, после сливания обоих растворов.
Так как по условию в полученном таким образом растворе содержится 35% кислоты, то ее концентрация там равна 0,35.
Таким образом, получаем: ![]() или х+у=3,5.
или х+у=3,5.
Если будем сливать равные объемы растворов по m литров, то
![]() - масса кислоты в полученном растворе,
- масса кислоты в полученном растворе,
2m - масса полученного раствора,
тогда
 - концентрация кислоты в полученном растворе.
- концентрация кислоты в полученном растворе.
По условию
 или
или ![]() .
.
Таким образом, получили систему двух уравнений
 Þ
Þ ![]() Þ
Þ ![]() Þ
Þ
Þ ![]() Þ
Þ ![]()
Ответ: в первом растворе содержится 1,64 л кислоты, во втором - 1,86 л.
Приведем некоторые указания к решению задач на растворы.
Основными компонентами этого типа задач являются:
а) массовая доля растворенного вещества в растворе;
б) масса растворенного вещества в растворе;
в) масса раствора.
Предполагают, что:
а) все получившиеся смеси и сплавы являются однородными;
б) смешивание различных растворов происходит мгновенно;
в) объем смеси равен сумме объемов смешиваемых растворов;
г) объемы растворов и массы сплавов не могут быть отрицательными.
Определения и обозначения.
Массовая доля растворенного вещества в растворе - это отношение массы этого вещества к массе раствора.
![]() (1)
(1)
где С- массовая доля растворенного вещества в растворе;
![]() - масса растворенного вещества в растворе;
- масса растворенного вещества в растворе;
![]() - масса раствора.
- масса раствора.
Следствия формулы (1):

Введем обозначения:
С1- массовая доля растворенного вещества в первом растворе;
С2- массовая доля растворенного вещества во втором растворе;
С- массовая доля растворенного вещества в новом растворе, полученном при смешивании первого и второго растворов;
m1(в-ва), m2(в-ва), m(в-ва) - массы растворенных веществ в соответствующих растворах;
m1(р-ра), m2(р-ра), m(р-ра) - массы соответствующих растворов.
Основными методами решения задач на смешивание растворов являются: с помощью расчетной формулы, «Правило сосудов», «Правило креста», графический метод, алгебраический метод.
С помощью расчетной формулы
В наших обозначениях, получим формулу для вычисления массовой доли вещества в смеси.
1. Масса полученного при смешивании раствора равна:
m(р-ра) = m1(р-ра) + m2(р-ра).
2. Определим массы растворенных веществ в первом и втором растворах:
m1(в-ва)= C1 m1(р-ра), m2(в-ва)= C2 m2(р-ра).
3. Следовательно, масса растворенного вещества в полученном растворе вычисляется как сумма масс веществ в исходных растворах:
m(в-ва) = m1(в-ва) + m2(в-ва) = C1 m1(р-ра) + C2 •m2(р-ра).
4. Таким образом, массовая доля растворенного вещества в полученном растворе равна:
![]() (1)
(1)
или
![]()
или
(4) ![]()
где ![]() - массы соответствующих растворов.
- массы соответствующих растворов.
5.Замечание: При решении задач удобно составлять следующую таблицу.
1-й раствор
2-й раствор
Смесь двух растворов
Масса растворов
m1
m2
m1 + m2
Массовая доля растворенного вещества
C1
C2
C
Масса вещества в растворе
C1m1
C2m2
C (m1 + m2)
На практике принцип, данный таблицы можно заменить схематическим рисунком
В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Правило сосудов.
В решении подобных задач помогает картинка. Изобразим сосуд с раствором схематично - так, как будто вещество и вода в нем не перемешаны между собой, а отделены друг от друга, как в коктейле. И подпишем, сколько литров содержат сосуды и сколько в них процентов вещества. Концентрацию получившегося раствора обозначим х.
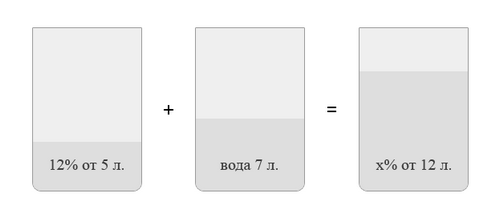
Первый сосуд содержал 0,12 ![]() 5 = 0,6 литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:
5 = 0,6 литра вещества. Во втором сосуде была только вода. Значит, в третьем сосуде столько же литров вещества, сколько и в первом:

«Правило креста»
«Правилом креста» называют диагональную схему правила смешения для случаев с двумя растворами.
I
 раствор С1 С- С2 массовые части I раствора
раствор С1 С- С2 массовые части I раствора

 С
С
II раствор С2 С1 -С массовые части II раствора
Слева на концах отрезков записывают исходные массовые доли растворов (обычно слева вверху-большая), на пересечении отрезков - заданная, а справа на их концах записываются разности между исходными и заданной массовыми долями. Получаемые массовые части показывают в каком отношении надо слить исходные растворы.
Сколько граммов 35%раствора марганцовки надо добавить к 325г воды, чтобы концентрация марганцовки в растворе составило 10%?.
Решим задачу по правилу « креста»
3
 5 10
5 10

 10
10
0 25
Значит, 325 г воды составляют 25 частей, а 35% раствор- 10 частей, или 325: 25 *10 = 130
Ответ 130 г.
Алгебраический метод
Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений.
Из ряда задач на проценты можно отдельно выделить задачи «о продуктах». То есть такие, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог - знайте, что на самом деле это задача на растворы. Сухие грибы получаются, когда из свежих испаряется вода. Свежие грибы мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно грибы, а не картошка
Задача 1.
Свежие грибы содержат 90% воды, а сухие 12 % воды. Сколько кг свежих грибов нужно взять, чтобы получилось 5сухих грибов
Масса, в кг
Содержание в %
Воды
Сухого вещества
Свежие грибы
х
90
100-90=10
Сухие грибы
5
12
100-12=88
Составим уравнение: 0,1х = 0,88 ![]() 5 и найдем х = 44.
5 и найдем х = 44.
Ответ: 44
Задача 2.
На столе лежал расколотый арбуз массой 10кг, содержащий 99% воды. Через некоторое время часть воды испарилась, и ее процентное содержание в арбузе понизилась до 96%. Найдите новую массу арбуза.
Вещество
Масса вещества (кг)
Процентное содержание воды
Процентное содержание сухого вещ-ва
Масса сухого вещества (кг)
Свежий арбуз
10
99%
1%
0,1
«Высохший» арбуз
х
96%
4%
0,04х
0,04х = 0,1
х = 2,5 кг.
Ответ: новая масса арбуза 2,5кг
Задача 3.
Индийский чай дороже грузинского на 25%.В каких пропорциях нужно смешать индийский чай с грузинским, чтобы получить чай, который дороже грузинского на 20%.
Решение.
Индийский чай дороже грузинского на 25%., индийский чай дороже грузинского в 1,25 раза. Чай, который хотим получить при смешивании, дороже грузинского на 20%, то есть дороже в 1,2 раза.
Составим схему
1
 0,05 грузинского чая
0,05 грузинского чая ![]()

 1,2
1,2
1,25 0,2 индийский чай![]()
Найдем отношение: ![]() :
:![]() =4:1
=4:1
Ответ:4:1.
Задача 4.
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
1-й раствор
2-й раствор
3-й раствор
Смесь растворов
Масса растворов
х
у
10
x+y+10
Массовая доля раст-воренного вещества
30
60
-
36
Масса вещества в растворе
0,3х
0,6у
-
0,36(x+у+10)
0,3х+0,6у=0,36 (х+у+10)
1-й раствор
2-й раствор
3-й раствор
Смесь растворов
Масса растворов
х
у
10
x+y+10
Массовая доля раст-воренного вещества
30
60
50
41
Масса вещества в растворе
0,3х
0,6у
5
0,41(x+у+10)
0,3х+0,6у+5=0,41(х+у+10),
0,3х+0,6у=0,36 (х+у+10)
x = 90-у
= 90-у
x=4у-60.
Решим уравнение 90-у=4у-60, у=30, х=90-30=60
Ответ: 60
Полезные формулы:
если величину x увеличить на p процентов, получим ![]()
если величину x уменьшить на p процентов, получим ![]()
если величину x увеличить на p процентов, а затем уменьшить на q%, получим ![]() .
.
если величину x дважды увеличить на p процентов, получим ![]()
если величину x дважды уменьшить на p процентов, получим ![]()
Заключение
Умение решать задачи является одним из основных показателей уровня математического развития школьников, глубины усвоения учебного материала. Поэтому любой экзамен по математике, любая проверка знаний содержит в качестве основной и, пожалуй, наиболее трудной части решение задач.
За время обучения в школе ученик решит огромное число задач, и, как правило, много из них однотипные. Однако в итоге некоторые ученики овладевают общим умением решения задач, а многие, встретившись с задачей незнакомого или малоизвестного вида, теряются и не знают, как ее решать.
И одной из причин такого положения является то, что одни ученики вникают в процесс решения задач, стараются понять, в чем состоят приемы и методы решения задач. Другие же не задумываются над этими, стараются лишь как можно быстрее решить заданные задачи. Эти учащиеся не анализируют в должной степени решаемые задачи и не выделяют из решения общие приемы и способы. Задачи зачастую решаются лишь ради получения ответа.
У большинства учащихся, весьма смутные, а порой, и неверные представления о сущности процесса поиска решения задач, о самих задачах. Как могут учащиеся решить сложную задачу, если они не представляют, из чего складывается анализ задачи? Как могут они решить задачу на доказательство, если они не знают, в чем смысл доказательства?
А можно ли научиться решать любую задачу?
Конечно, любые задачи научиться решать невозможно, ибо как бы хорошо ученик не умел решать задачи, всегда может встретиться такая, которую он решить не сможет.
Ясно, что рассчитывать на изображение методики обучения решению задач, пригодной для всех детей и во всех случаях - все равно, что искать универсальное лекарство от всех болезней. Практическая ценность обучения школьников решению текстовых задач разнообразными способами в современных условиях заключается совсем не в том, чтобы раз и навсегда вооружить их приемами решения различных задач, которые будут возникать в дальнейшем обучении, а в том, что оно обогатит их опыт мыслительной деятельности. Ведь определенный прием решения задач может быть просто забыт или вытеснен в дальнейшем обучении общим приемом. Для того, чтобы развитие качества, таких как сообразительность, смекалка, не было подобным результатом процесса обучения решению текстовых задач, а было закономерным планируемым результатом обучения, необходима специальная организация самого процесса обучения.
При решении задач у учащихся 5 класса возникали следующие трудности:
1) трудности, связанные с разделением условия на логические составляющие;
2) трудности в выборе схематической записи для конкретной задачи, ее оформлении;
3) в выборе величины, которую необходимо обозначить переменной «х».
Эти трудности возникли из-за того, что:
1) учащиеся неосознанно читали условия задачи;
2) как следствие неосознанного чтения задачи, не могли выявить процессы, описываемые в задаче.
Поэтому учащиеся не видели, что им дано, а какие величины можно брать в качестве неизвестной.
В 6-ом классе возникали трудности в установлении вида зависимости и в решении пропорции.
Первая трудность связана с тем, что учащиеся не пытались анализировать закономерности, которые встречались им в жизни. Они их, очевидно, просто не видели.
Вторая трудность была связана с том, что учащиеся на тот момент плохо владели умением применять свойство пропорции, что в свою очередь приводило к неправильным результатам в вычислениях.
Очень эффективно проводить на уроке либо фронтальную работу, либо давать учащимся задания на карточках для индивидуальной работы. Со слабыми учащимися надо проводить отдельные консультации, на которых им кроме указанных заданий можно предложить самостоятельно воспроизвести решение задачи, разобранной на уроке. Так как решать задачи учащимся придется в течение всего обучения, то им надо объяснить необходимость решать задачи с помощью составления уравнений. В конце 60-х годов ХХ века арифметические способы решения задач посчитали анахронизмом и перешли к раннему использованию уравнений. Но без достаточной подготовки мышления учащихся это оказалось малоэффективным.
Таким образом, можно сделать следующие выводы:
1) Исторически люди пришли к применению уравнений, обобщая решения задач, в которых приходилось оперировать с неизвестным числом. Ребёнок должен пройти тот же путь - сначала рассуждать о «частях», опираясь на воображаемые действия с конкретными предметами или величинами, и лишь потом прийти к применению уравнений. За этот путь говорят и особенности мышления учащихся, тяготеющего к оперированию наглядными образами.
2) На данном этапе обучения (5-6 класс) арифметические способы решения задач имеют преимущество перед алгебраическими уже потому, что результат каждого отдельного шага в решении по действиям имеет совершенно наглядное и конкретное истолкование, не выходящее за рамки опыта учащихся. Мышление пятиклассников конкретно, и развивать его надо в деятельности с конкретными объектами и величинами или их образами, чем мы и занимаемся при арифметическом решении задач.
3) Несмотря на небольшое количество часов, отведённое программой на изучение математики (5 часов в неделю), можно продумать и организовать работу с задачами таким образом, что ребёнок, опираясь на наглядность, будет переходить от простого к сложному, от практических действий с предметами к воображаемым действиям с данными в задаче величинами. Тем самым будет достигнута истинная цель обучения, заключающаяся не столько в освоении школьниками конкретных способов деятельности, сколько в развитии их мышления и практических умений в процессе освоения этих способов деятельности.
Библиография
-
Аргинская И.И., Вороницына Е.В. Особенности методики работы по обучению учащихся решению текстовых задач.// Начальная школа, 2005 №24
-
Арифметика: Учебник для 5 кл./ С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин - М.: Просвещение, 2003
-
Арифметика: Учебник для 6 кл./ С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин - М.: Просвещение, 2000
-
Математика: Учебник для 5 кл./ Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков,С.И.Шварцбурд - М.: Мнемозина, 2004
-
Математика: Учебник для 6 кл./ Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков,С.И.Шварцбурд - М.:Просвещение, 1994
-
Математика: Учебник для 5 кл./ Под ред Г.В.Дорофеева, И.Ф. Шарыгина - М.:Просвещение, 2003
-
Математика: Учебник для 6 кл./ Под ред Г.В.Дорофеева, И.Ф. Шарыгина - М.:Дрофа, 2000
-
Программа по математике: авт. М.И. Моро, Ю.М. Колягин, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова//Программы общеобразовательных учреждений, нач. классы (1 - 4) ч.1. - М.: «Просвещение», 2002
-
Программа по математике: авт. Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд //Программы для общеобразовательных школ, гимназий, лицеев, 5-11 кл. - М.: Дрофа, 2000.
-
Саговская Е.Н. Активизация работы ученика над арифметической задачей //Из опыта преподавания математики в 5-7 классах средней школы - М.: Учпедгиз, 1954
-
Саговская Е.Н. Методические разработки по арифметике - М.: Учпедгиз, 1959
-
Талызина Н.Ф.Формирование общих приёмов решения арифметических задач//Формирование приёмов математического мышления - М.: ТОО «Вентана --Граф», 1995
-
Шарова О.П. Сюжетные задачи в обучении математике
-
Шарова О.П. О некоторых аспектах методики обучения учащихся решению сюжетных задач арифметическим методом
-
Шевкин А.В. Обучение решению текстовых задач в 5-6 классах. - М.: Русское слово, 2002
-
Шевкин А.В. Текстовые задачи в школьном курсе математики //Математика, 2005 - №17-20.
-
Фридман Л.М. Как научиться решать задачи - М.: Просвещение, 1984
-
) Волович М.Б. Ключ к пониманию математики. - М., 1997.
-
Глейзер Г.И. История математики в школе: 4 - 6 классы: Пособие для учителей. - М., Просвещение, 1984.
-
Гусев В.А. Как помочь ученику полюбить математику. - М., 1994.
-
Далингер В.А. Обучение учащихся решению текстовых задач методом составления уравнений. - Омск, 1991.
-
Захарова А.Е. Текстовые задачи в курсе алгебры основной школы. Учебно-методические материалы спецкурса по методике преподавания математики «Избранные вопросы обучения алгебре в основной школе». М.: «Прометей», 2002.
-
Колягин Ю.М. Задачи в обучении математике: т.2. - М.: Просвещение, 1997.
-
Крутецкий В.А. Основы педагогической психологии. - М.: Просвещение, 1972.
-
Леонтьев А.Н. Деятельность. Сознание. Личность. - М.: «Мысль», 1975.
-
Лященко Е.И. Проблема задач в школьном курсе математики. Задачи как цель и средство обучения математике учащихся средней школы. - ЛГПИ им. А.И. Герцена, 1981.
-
Математика в 5 классах: В помощь учителю / Под ред. А.И. Маркушевича. - М.: Просвещение, 1971.
72