Урок по теме: Задачи на определение вероятности события

Задачи по теории вероятностей и статистике. Подготовка к ОГЭ по

математике.

Вы, наверное, не раз слышали или сами говорили "это возможно", "это невозможно", это обязательно случиться", "это маловероятно"

Такие выражения обычно употребляют, когда говорят о возможности наступления события, которое в одних и тех же условиях может произойти, а может и не произойти.

Случай, случайность - с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная ошибка. Этот ряд можно продолжать до бесконечности. Казалось бы, тут нет места для математики - какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности - они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями

Слово "событие" в быту применяют к значительным явлениям (день рождение, экзамен, свадьба), а в математике - ко всем возможным исходам рассматриваемой ситуации. Например, при бросании игральной кости событие- это выпадение той или иной грани.

Работаем устно

Какими буквами обозначаются события? Приведите примеры достоверных событий (смена дня и ночи); невозможных событий (2012 год наступит 1 июля 2011 года); возможных или случайных (в мае выпадет снег); равновозможных или равновероятных (подкидывание монеты).

Какие из следующих событий - возможные (случайные), достоверные, невозможные

• Черепаха научится говорить

• Вода в чайнике, стоящем на горячей плите закипит

• День рождения вашего друга - 30 февраля

• Вы выиграете, участвуя в лотерее

• Вы не выиграете, участвуя в беспроигрышной лотерее

• На следующей неделе испортится погода

• Вы нажали звонок, а он не зазвонил

• После четверга будет пятница

• Летом у школьников будут каникулы

• По окончанию 9 класса учащиеся будут сдавать экзамен по алгебре

• Зимой выпадет снег

• При включении света, лампочка перегорит

• Вы выходите на улицу, а вам навстречу идёт слон

• Завтра пойдёт дождь

Ответы:

Вспомним классическое определение вероятности

Впервые вероятность случайных событий в играх вычислили в XVII веке французские математики Блез Паскаль и Пьер Ферма. Они подсчитали число шансов события из общего возможного числа равновероятных исходов. Они вывели классическое определение вероятности (повторить перед решением задач).

Классическое определение вероятности: отношение m к n.

m - число шансов события А, n - общее число равновероятных исходов.

Решаем задачи комментированно у доски

1.Хорошо перетасуем колоду из 36 карт, случайно вынем 1 карту. Какова вероятность того, что вытянут туз?

2.В лотерее 100 билетов, из них 5 выигрышных. Какова вероятность проигрыша?

3. В ящике лежат 8 красных,2 синих, 20 зеленых карандашей. Вы наугад вынимаете карандаш. Какова вероятность того, что это красный карандаш? Чёрный карандаш?

Решение задач

1.

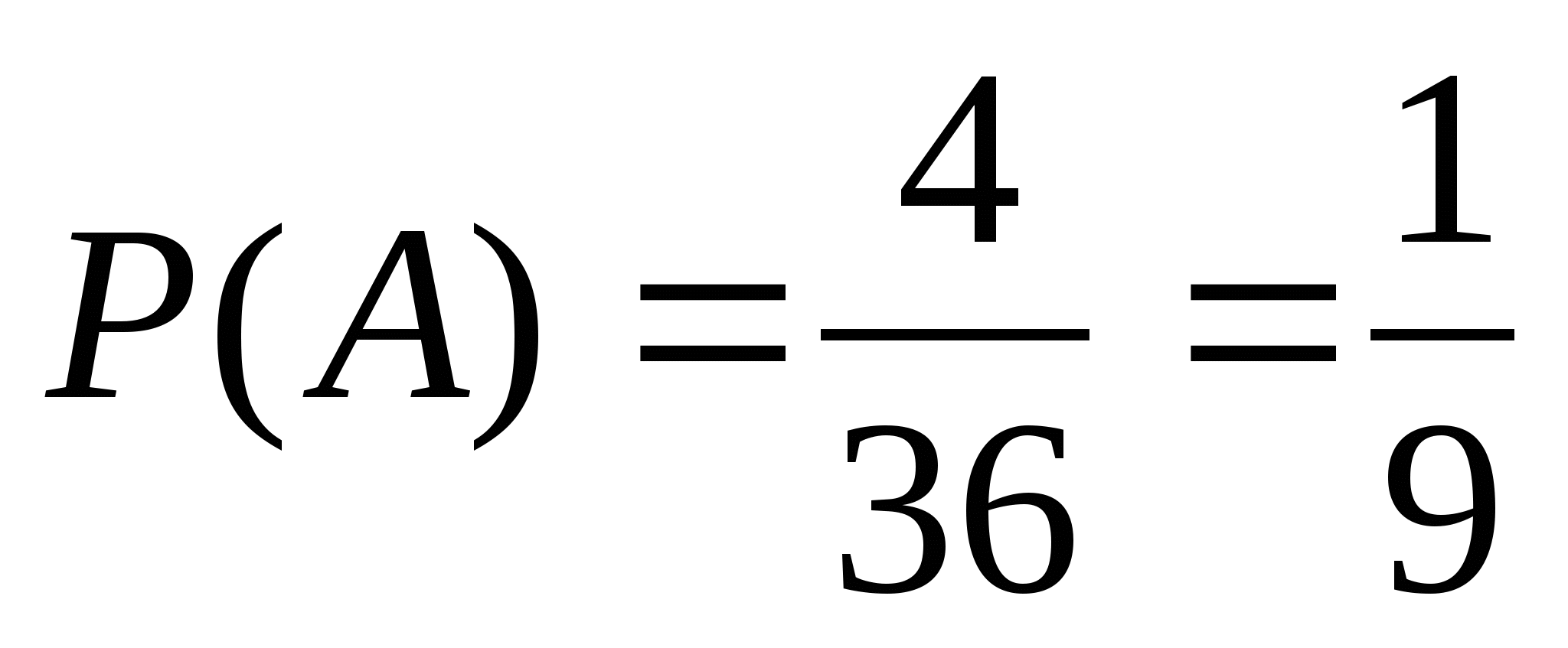
2.

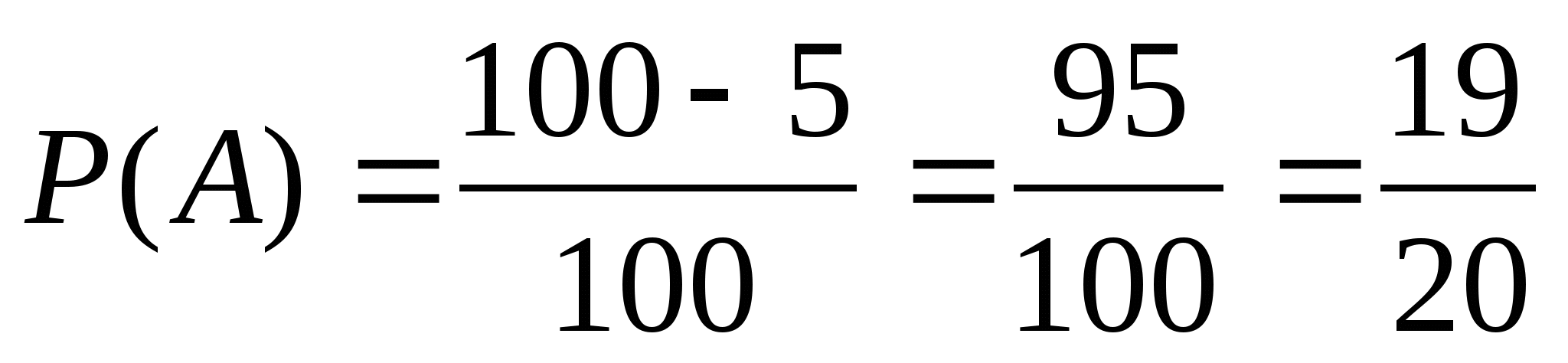
3.А={вынут красный карандаш},

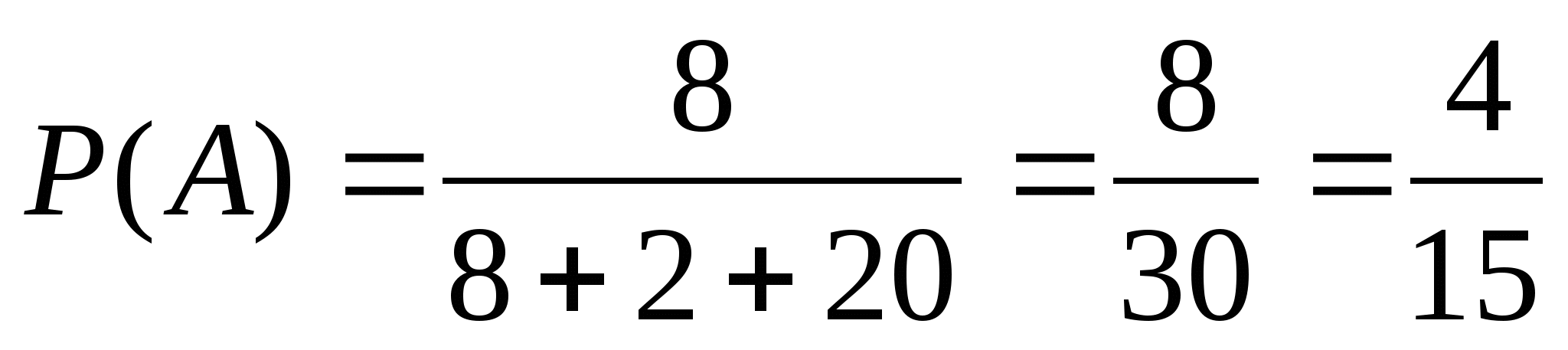
В={вынут чёрный карандаш},

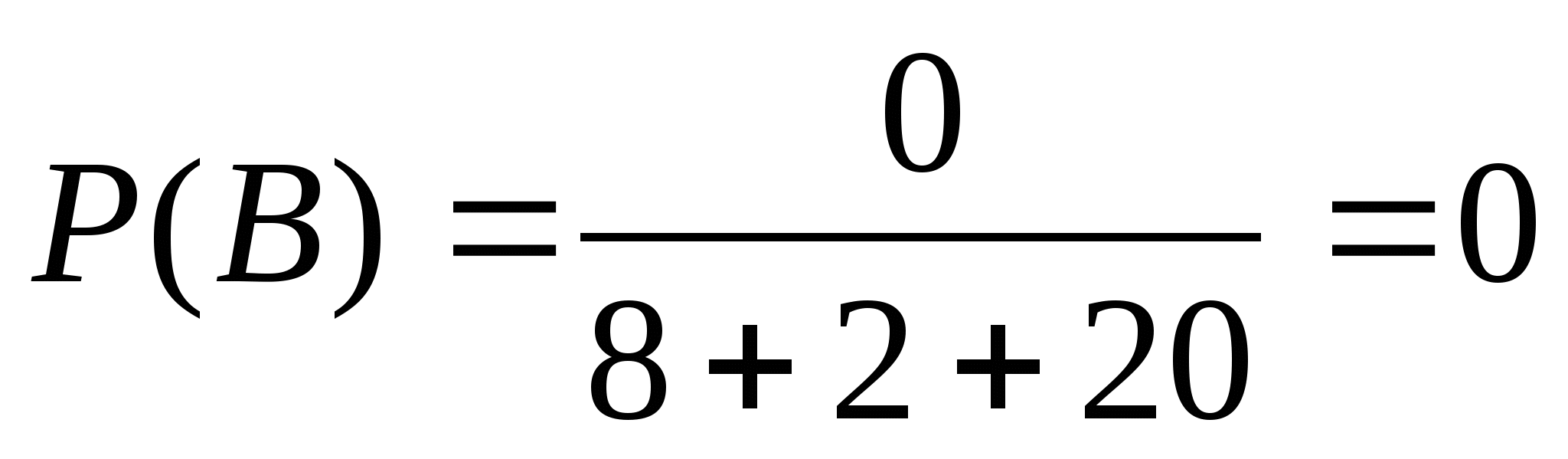
Задачи для самостоятельного решения

1.На экзамене -24 билета. Андрей не разобрался в одном билете и очень боится его вытянуть. Какова вероятность, что Андрею достанется несчастный билет?

2.В лотерее 10 выигрышных билетов и 240 билетов без выигрыша. Какова вероятность выиграть в эту лотерею, купив один билет?

3. В ящике лежат 8 красных,2 синих, 20 зеленых карандашей. Вы наугад вынимаете карандаш. Какова вероятность того, что это зелёный карандаш? Не желтый карандаш?

Решение задач

1.

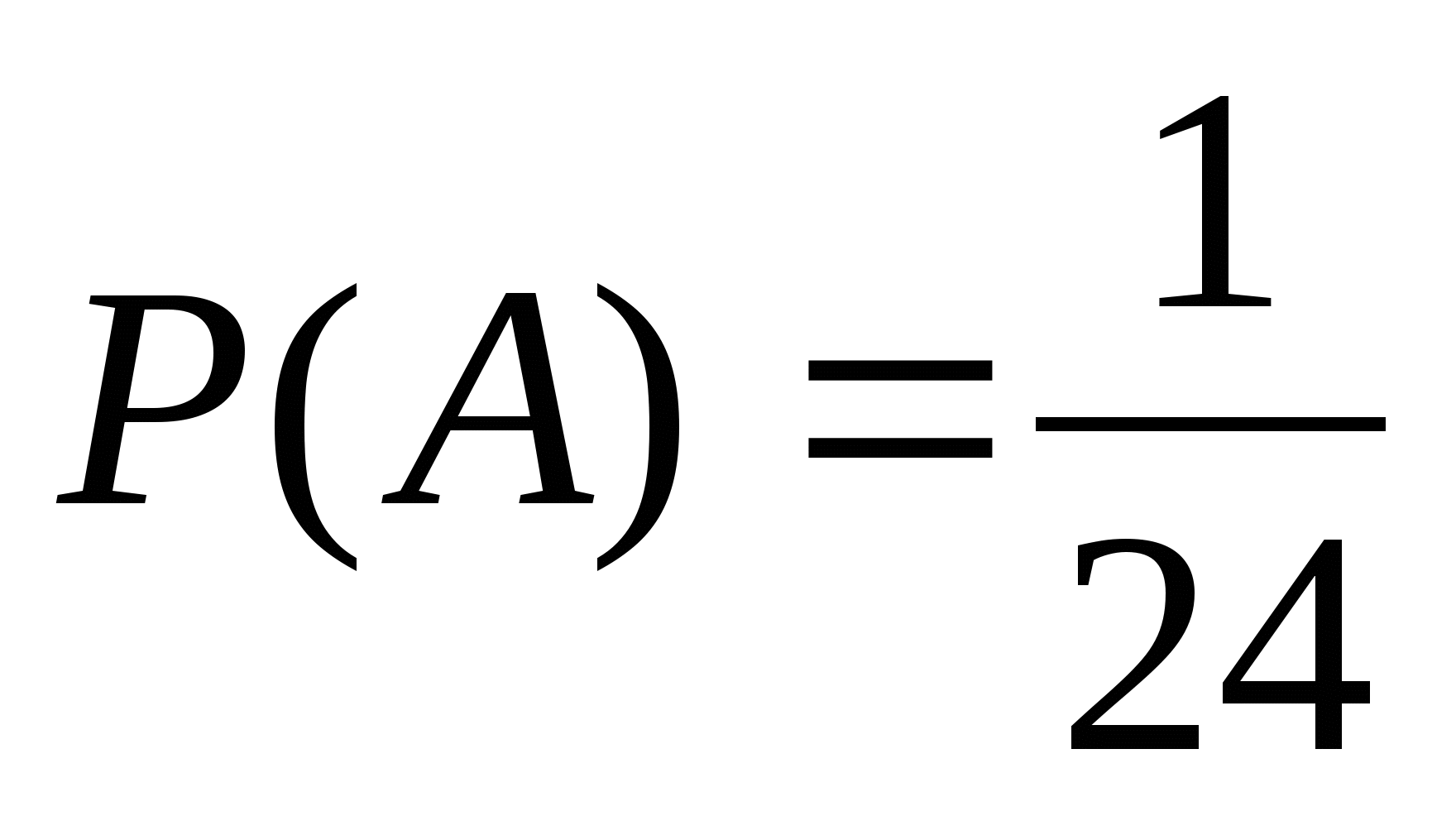
2.

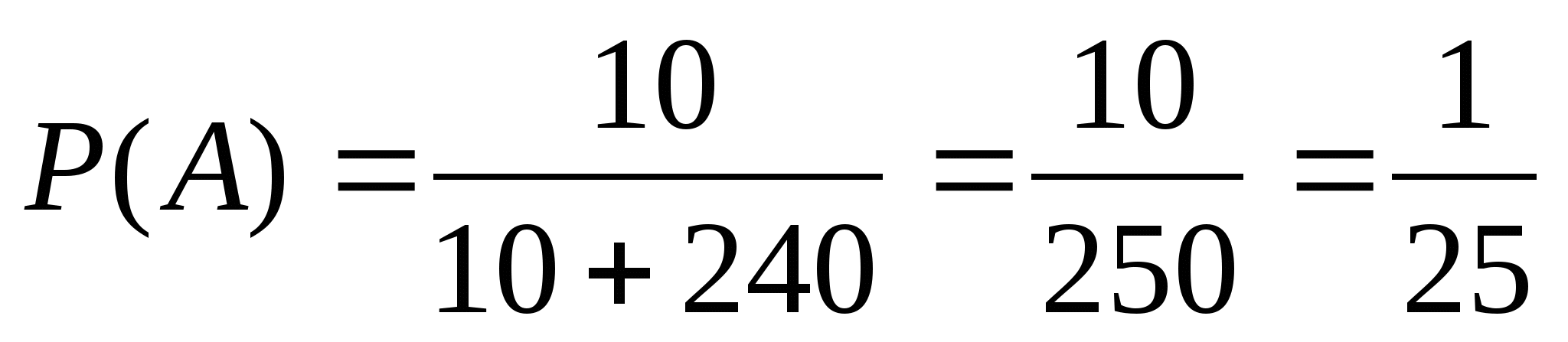
3. А={вынут зелёный карандаш},

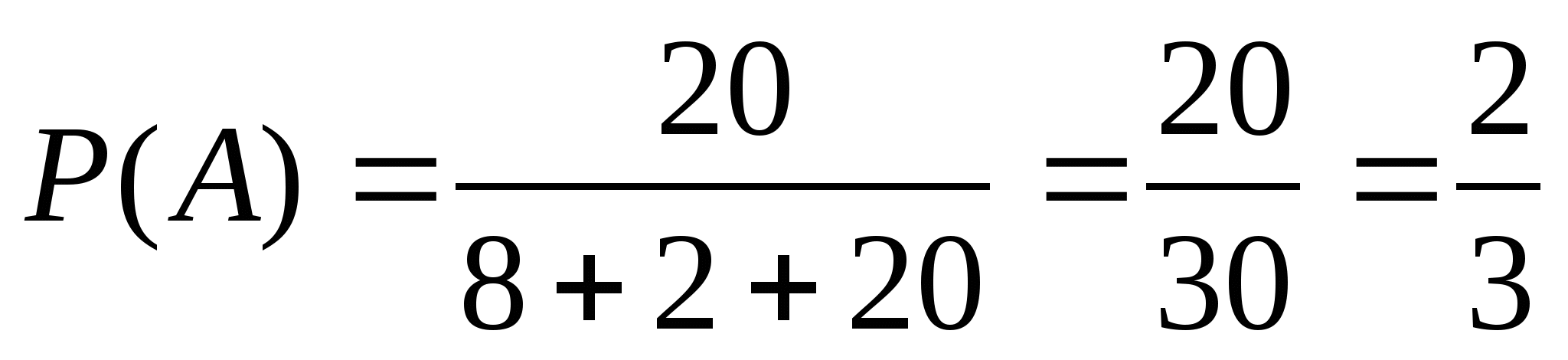
В={вынут не жёлтый карандаш},

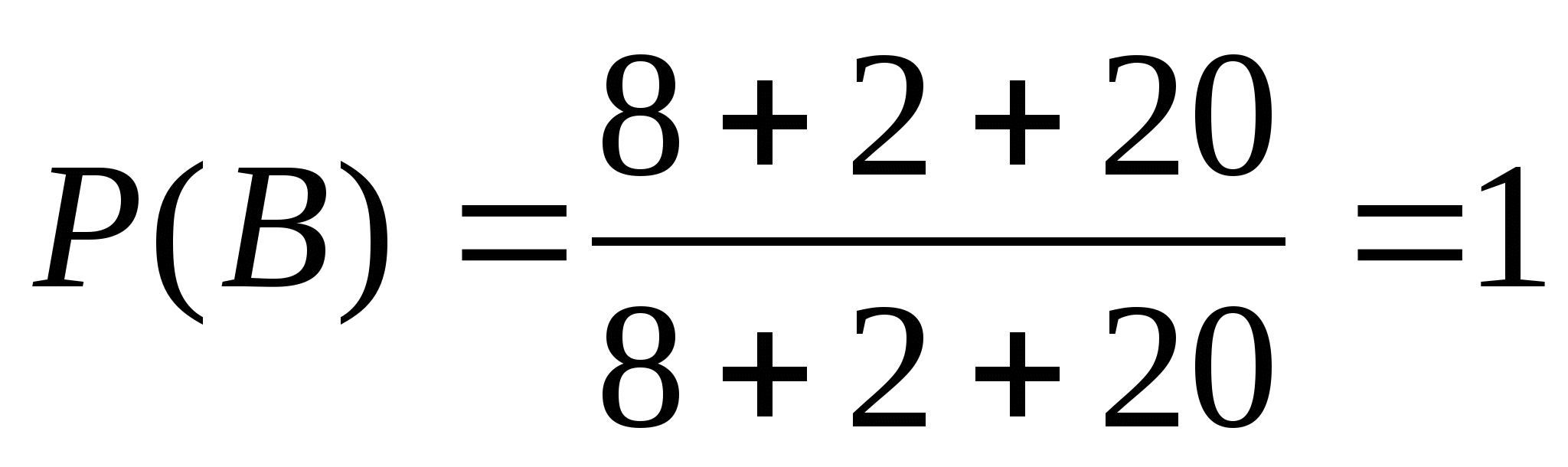
Статистика

Статистика - наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово "статистика" происходит от латинского слова status, которое означает "состояние, положение вещей". Результаты статистических исследований широко используют для практических и научных выводов.

У трех друзей Петра, Артёма- к концу четверти по алгебре оказались следующие отметки:

Петр: 5;4;4;3;5;4;5;5;4;3;5;5;

Артём: 3;3;2;3;4;4;4;3;3;2;4;4.

Запишите упорядоченный ряд данных для каждого ученика и ответьте на вопросы:

а) Какой средний балл имеет к концу четверти каждый ученик?

б) Какова наиболее типичная, характерная отметка каждого из них?

в) Какова средняя отметка каждого ряда?

г) Чему равна разность между наибольшей и наименьшей отметками?

д) Сколько раз в четверти был опрошен ученик?

Какую отметку вероятнее всего получит каждый из друзей за четверть?

Вопросы:

- Какой статистической характеристикой можно назвать средний балл (среднее арифметическое)?

- Какой статистической характеристикой можно назвать наиболее типичную отметку (частота)?

- Какой статистической характеристикой можно назвать среднюю отметку каждого ряда (медиана)?

- Какой статистической характеристикой можно назвать разность между наибольшей и наименьшей отметкой (размах)?

- Какой статистической характеристикой можно назвать число, которое показывает, сколько раз был спрошен ученик (объём)?

• Решите самостоятельно (после выполнения задания- взаимопроверка с комментированием)

В городе пять школ. В таблице приведен средний балл, полученный выпускниками каждой из этих школ за экзамен по математике. Найдите средний балл выпускного экзамена по математике по всему городу?

1

2

3

4

5

Количество выпускников

30

60

40

60

60

Средний балл

66

55

60

64

58

Решение: Чтобы найти средний балл выпускного экзамена по математике по всему городу, нужно сложить баллы всех выпускников и поделить на общее количество выпускников.

1. Общее количество выпускников равно 30+60+40+60+60=250

2. Если умножить количество учеников в школе на средний балл по школе , то получиться сумма баллов в этой школе, а если сложить все такие произведения , то сумма всех баллов по городу равна

30 × 66+60× 55+40 ×60+60 ×64+60 ×58= 1980+3300 +2400+ +3840+3480= 15000

3. Средний балл по городу равен 15000:250=60

Ответ: 60.

При каких значениях х среднее арифметическое ряда чисел 1, 2, 3, 4, х будет равно 3.

Ряд чисел: 1, 2, 3, 4, х

Среднее арифметическое: X = 3

Запишем среднее арифметическое заданного ряда:

X =(1+2+3+4+х):5=(10+х):5=3.

Решим уравнение:

(10+х):5=3, х=5

Ответ: х=5

Задачи для самостоятельного решения.

Задача №1. Телевизор у Любы сломался и показывает только один случайный канал. Люба включает телевизор. В это время по одному каналу из двадцати пяти показывают кинокомедии. Найдите вероятность того, что Люба попадет на канал, где комедия не идет.

Ответ: 0,96

Задача №2. Телевизор у Любы сломался и показывает только один случайный канал. Люба включает телевизор. В это время по двадцати пяти каналам из пятидесяти показывают кинокомедии. Найдите вероятность того, что Люба попадет на канал, где комедия не идет.

Ответ: 0,5

Задача №3 . Валя выбирает трехзначное число. Найдите вероятность того, что оно делится на 50.

Ответ: 0,02

Задача №4. Вова выбирает трехзначное число. Найдите вероятность того, что оно делится на 49.

Ответ: 0,02

Задача № 5. Женя выбирает трехзначное число. Найдите вероятность того, что оно делится на 2

Ответ: 0,5

Задача № 6. Максим выбирает трехзначное число. Найдите вероятность того, что оно делится на 98.

Ответ: 0.01

Задача № 7. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 4.

Ответ: 0,25

Задача № 8. Леша наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 0.

Ответ: 0,1

Задача № 9. На экзамене 40 билетов, Оскар не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.

Ответ: 0,3

Задача № 10. Саша с папой решили покататься на колесе обозрения. Всего на колесе десять кабинок, из них 5 - синие, 2 - зеленые, остальные - красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Саша прокатится в красной кабинке.

Ответ: 0,3

Задача № 11. В каждой пятидесятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Наташа покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Наташа не найдет приз в своей банке?

Ответ: 0,98

Задача № 12. В фирме такси в данный момент свободно 20 машин: 2 черных, 5 желтых и 13 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.

Ответ: 0,25

Задача № 13. На тарелке 30 пирожков: 13 с мясом, 11 с капустой и 6 с вишней. Антон наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.

Ответ: 0,2

Задача № 14. На тарелке 20 пирожков: 4 с мясом, 10 с капустой и 6 с вишней. Жора наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.

Ответ: 0,3